地下管廊基坑工程鲁棒性分析及风险评估
2021-03-04孙靖涵楼恺俊
黄 柏,孙靖涵,林 统,楼恺俊
(1.浙江交工集团股份有限公司地下分公司,浙江 杭州310051;2.浙江理工大学基础结构技术研究所,浙江 杭州310018;3.浙江省装配式混凝土工业化建筑工程技术研究中心,浙江杭州310018)
随着国内城市化进程的深入,地下综合管廊基坑工程越来越多的处于敏感环境下,工程难度逐渐加大,地下连续墙支护结构是如今地下管廊基坑工程的常用支护形式,因此有必要对地下综合管廊进行风险评估[1]。在开挖软黏土地区等变形敏感地区,由于岩土力学参数的不确定性所产生的工程风险性会增大,有必要研究在评估和设计阶段考虑岩土力学参数可能带来的安全问题。
对于岩土基坑工程的评估,最常用的手段为数值模拟,基坑工程数值分析的精确度取决于合理的土体本构模型及土体参数比例关系[1-2]。根据前人经验,在分析软黏土地区基坑工程问题时,宜采用小应变土体硬化模型(HS-Smallmodel,HSS)[3]。由于获得HSS模型土体参数相关试验的经济成本高,有必要对杭州富阳典型地区的HSS模型土体参数进行研究。
如今基坑工程的设计方法大多采用的是确定性设计方法与可靠度设计方法,然而这两种方法均无法考虑岩土力学参数变异系数的不确定性对支护结构整体功能的影响。针对该情况,鲁棒性设计可考虑不可控参数的波动性,进而精确评估系统对于不可控参数变异产生的敏感度。目前,黄宏伟等[4]已将鲁棒性设计运用于重力式挡土墙设计;赵密等[5]对桩下独立基础进行了鲁棒性设计与分析。
本文依托杭州市富阳区金桥北路市政综合管廊基坑工程案例,以PLAXIS 2D为平台,基于正交试验法确定适用于杭州富阳典型地区的HSS模型土体参数比例关系;以该工程案例对确定性设计方法、可靠度设计方法及鲁棒性设计方法进行比较,分析了地下连续墙鲁棒性设计的必要性与重要性。
1 工程案例
1.1 工程概况
杭州市富阳区金桥北路市政综合管廊工程位于富阳主城区,为一条南北向的管廊。基坑开挖标准段深约8 m。主体围护结构采用850 mm厚TRD水泥土地下连续墙内插H型钢,墙深26 m。基坑设1道混凝土支撑及1道钢支撑。本文选取剖面进行分析,模型示意图及二维典型剖面图见图1。
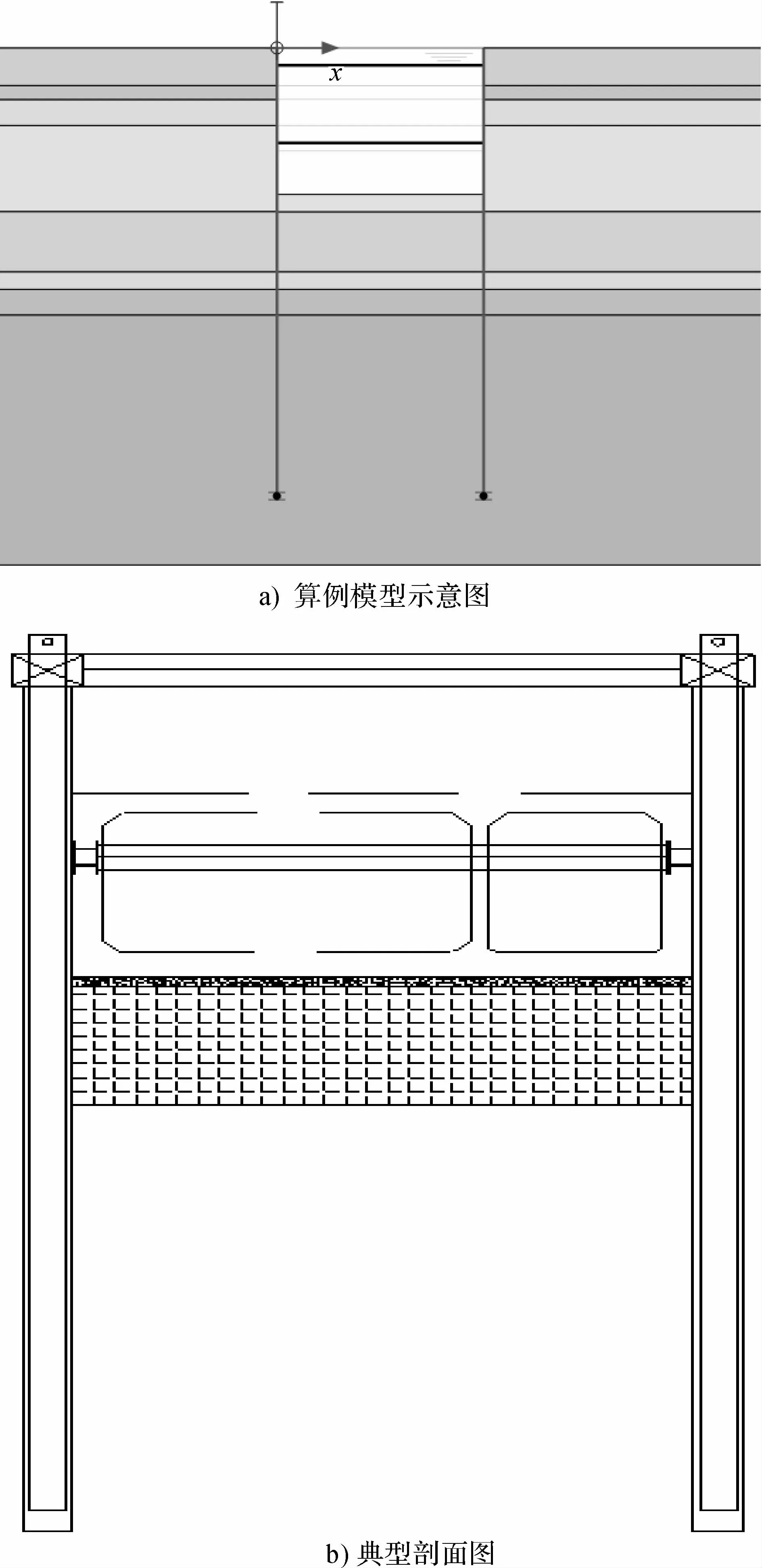
图1 案例示意图
1.2 工程地质条件
场地典型地层的土性参数根据金桥北路管廊项目详勘报告所得,见表1。表1中,γ为重度,Es为压缩模量,c为固结快剪粘聚力,φ为固结快剪内摩擦角。
本工程案例中的土层中上部为淤泥质土层,对于这类典型杭州软黏土地区,岩土力学参数的不确定性对工程各阶段的影响均较为明显,是风险控制主要的不可控因素,因此本文借助该工程案例,对地下综合管廊各阶段的风险进行分析。
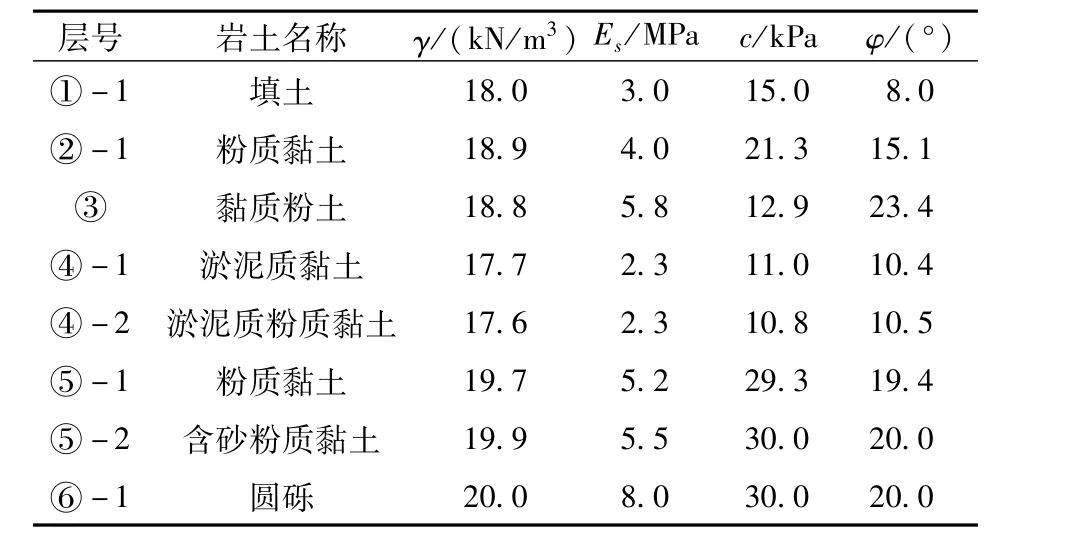
表1 土层物理力学参数
2 基于HSS模型的正交试验法
对于复杂工况下的岩土工程的建设过程,大多数情况下有评估、设计、施工等重要环节。其中岩土工程的评估为设计、施工提供指导建议,评估最为关键的手段之一为数值分析,决定数值分析精度的最关键因素为选取合理的土参模型和模型参数比例关系。因此本文借助PLAXIS 2D平台以本工程案例典型剖面对HSS模型参数进行分析。
2.1 HSS模型参数
对于杭州软黏土地区,土体多处于小应变状态,因此在分析杭州软黏土地区岩土工程数值问题时,宜采用小应变土体硬化模型。
小应变土体硬化模型(HS-Smallmodel)是一种反映土体小应变与卸荷特征的土体本构模型。其参数包含:有效粘聚力c′,有效内摩擦角φ′,土的剪胀角ψ,正常固结条件下静止侧压力系数k0,刚度应力水平相关幂指数m,参考应力pref,加卸载泊松比νur,三轴排水剪切实验的参考割线模量,固结实验中的参考切线模量,三轴排水剪切试验的参考卸荷再加载模量破坏比Rf,及两个反映土体小应变性质的参数:小应变刚度试验初始参考模量,阈值剪应变 γ0.7。
在传统方法中,获取以上一套HSS模型参数需要大量的土工室内试验,尤其是Gref0需要弯曲元试验、共振柱试验和扭剪试验等高级试验,需要大量的费用和时间。为此本文借助PLAXIS 2D平台,采用正交试验法来获取HSS模型参数比例关系。
2.2 数值分析建模
本文选取典型标准剖面,二维有限元模型尺寸取:长30 m、深35 m。850 mm厚TRD地下连续墙采用板单元模拟,第一道混凝土支撑和第二道钢支撑均采用梁单元进行模拟,以上结构在变形较小时,均考虑为弹性材料,底板以下3 m土层采用高压旋喷桩加固。
2.3 正交试验法
基于前人经验选定初始HSS模型参数比例关系,通过正交试验法进行二维有限元模拟。对比数值解和实测值,考虑误差范围,获得杭州富阳典型黏土地区HSS模型参数比例关系。
其中c′和φ′由勘查报告提供;ψ的取值按经验公式;νur根据前人研究取0.2;m的取值,黏性土m=0.8,砂土和粉土 m=0.5;Rf取 0.9;对于 γ0.7:砂性土取2×10-4,黏性土取1×10-4;k0和 pref的取值按PLAXIS选取;勘察报告中一般只提供,本文通过正交试验法重点获取间的相关比例关系。试验参数选取初终值对比见表2。
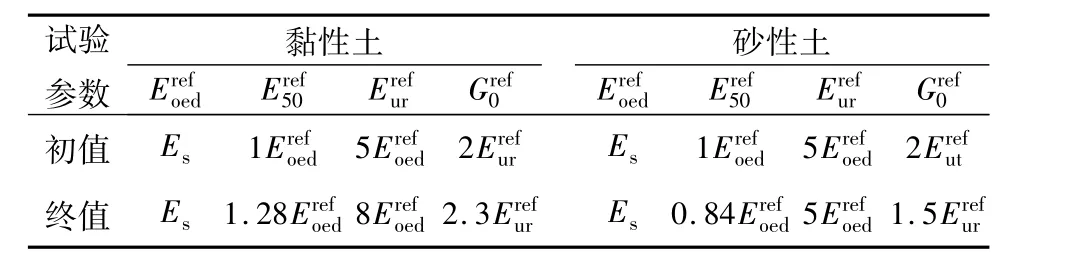
表2 正交试验法参数初终值对比
开挖至底时,墙体水平位移l在TRD地下连续墙深度H上的实测值与数值解的比较,见图2。
由图2所知,采用HSS模型参数终值比例关系获得的地下连续墙水平位移数值解与实测值在误差范围内基本一致,因此本次正交试验法获得的富阳典型软黏土地区HSS模型重要参数比例关系在之后的类似地区的数值模拟中具有较高的实际应用价值,该比例关系总结见表3。

表3 富阳典型地区HSS参数选取
3 地下连续墙鲁棒性分析
传统岩土工程的设计方法大多采用的为确定性设计方法与可靠度设计方法。然而在实际工程中,岩土力学参数的变异系数是可变的,它的波动性对工程安全性产生的影响程度亟待探讨。本文对富阳工程案例分别运用三类设计方法进行分析讨论,旨在说明鲁棒性设计方法的必要性。
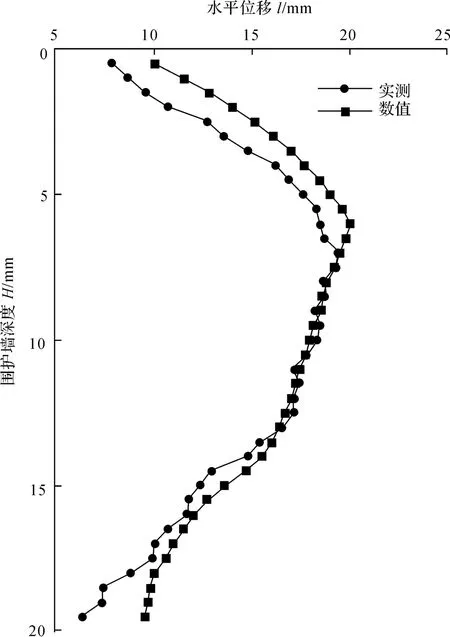
图2 实测与数值水平位移随深度的变化
3.1 确定性设计方法
确定性设计方法是指考虑岩土力学参数为定值时根据目标函数确定结构参数。根据建筑基坑工程技术规范[7],隆起、墙体倾覆和支护结构侧移是地下连续墙支护结构的三种破坏模式。因此本文工程案例的TRD地下连续墙的破坏模式如上所述。
根据建筑基坑工程规范[6],隆起破坏模式的目标函数为:
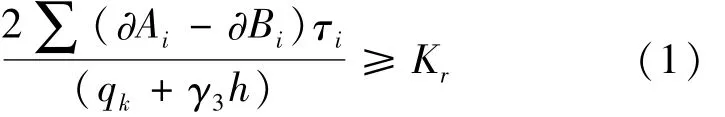
式中:∂Ai和∂Bi为滑弧面与第i层土层的交点Ai、Bi与下层支点的连线与竖直方向的夹角;
τi为末道支撑底部至围护墙底的深度范围的第i层土层中间深度点的抗剪强度,kPa;
qk为地面荷载,kPa;
γ3为地面至开挖深度范围内的各土层天然重度的加权平均值;
h为地面至开挖面深度,m;
Kr为抗隆起安全性系数,根据规范要求取值。
根据建筑基坑工程规范[6],倾覆破坏模式的目标函数为:

式中:MRC为抗倾覆力矩;
MOC为倾覆力矩;
Kf为围护墙抗倾覆安全系数,根据规范要求取值。
根据平面弹性地基梁法,支护结构侧移破坏模式的目标函数为:
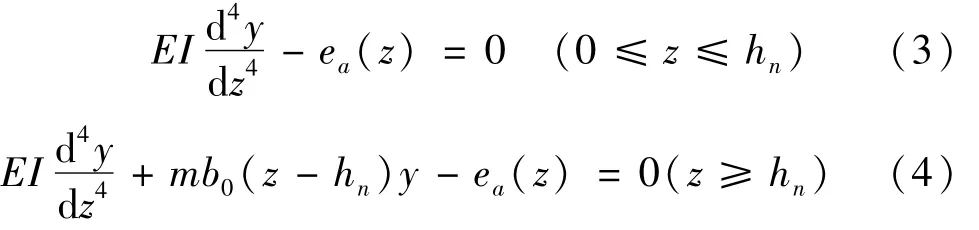
式中:EI为支护结构的抗弯刚度;
y为支护结构侧移量;
z为深度;
m为地基土水平抗力比例系数;
ea(z)为z深度下的主动土压力;
hn为第n步的开挖深度。
3.2 可靠度设计方法
可靠度设计方法是指考虑岩土力学参数变异系数为定值,以概率理论进行极限状态设计。
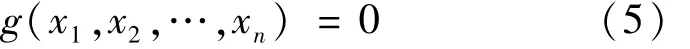
式中:g为结构功能函数;
xi为变量。
结构功能函数应符合如下要求:

式中:R(x)为结构的抗力;
S(x)为结构的外力。
通过功能函数计算相应失效概率pf如下,
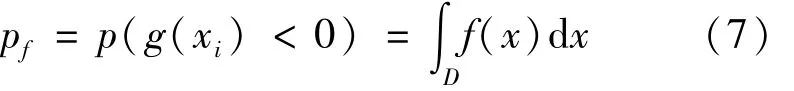
式中:f(x)为概率密度函数;
D为失效域。
由于实际结构极限状态方程的复杂性、非线性等原因,可靠度一般以可靠度指标度量,可靠度指标采用一次二阶矩法或蒙特卡洛法进行计算。结构的失效概率与可靠度指标具有如下关系:

式中:pf为失效概率;
φ为标准正态分布函数。
3.3 鲁棒性设计方法
岩土力学参数变异系数的波动性会导致支护结构破坏模式的失效概率出现变化,并最终可能影响支护系统整体功能,使得工程风险性增加。岩土力学参数变异系数在工程勘察报告中仅能获得一个大致取值范围,其变异系数标准差需要通过理论计算获得,变异系数的标准差σcov可依据3-σ法计算获得。

式中:Hcov为变异系数上限;
Lcov为变异系数下限。
地下连续墙鲁棒性设计是通过改变结构参数来降低支护系统破坏模式对岩土力学参数变异系数的标准差的影响程度。即在岩土力学参数变异系数不确定的情况下,通过改变结构设计参数使岩土力学参数变异系数的不确定性对支护系统破坏模式的失效概率的影响程度达到最低,使地下连续墙支护结构具备高鲁棒性。
3.4 各设计方法比较
为说明鲁棒性设计方法与确定性设计方法及可靠度设计方法的区别,表明岩土力学参数变异系数及变异系数的标准差均会使得支护结构破坏模式的失效概率在结构参数下发生波动。本工程案例原设计方法为可靠度设计方法,对案例中的地下连续墙支护结构设计参数{H=26 m;d=0.85 m;h3=3 m}分别根据式(1)~(9)对三类破坏模式的失效概率以确定性设计方法、可靠度设计方法和鲁棒性设计方法分别进行求解计算,进行比较。
本案例隆起破坏、墙体倾覆破坏和支护结构侧移破坏均为二级延性破坏。依据建筑结构可靠度设计统一标准[7],三种失效模式对应的可靠度指标为3.2,相应的失效概率为0.000 69。本案例土体参数变异系数的取值范围为2%~10%,变异系数均值为6.5%,变异系数标准差为1.17%。
计算结果见图3。
由图3可知,该工程案例采用的是可靠度设计方法,其结构参数对应的各破坏模式的失效概率均满足要求,当对应结构参数采用确定性设计方法时,已大大满足失效概率要求,然而若考虑岩土力学参数变异系数的标准差采用鲁棒性设计计算时,该结构参数组合并不能满足要求。
因此对于典型软黏土地区,岩土力学参数的不确定性会大幅增加,采用确定性设计方法对工程设计而言过于危险;采用可靠度设计方法在某些时候也会出现风险性,采用鲁棒性设计方法获取结构参数可以有效规避岩土力学参数不确定性带来的影响,使基坑工程的风险性降低。

图3 三类设计方法对比
4 结 语
1)依托杭州市富阳区金桥北路市政综合管廊基坑工程案例,对工程典型剖面进行HSS模型数值反分析,得到了适用于杭州市富阳区典型的HSS模型参数比例关系的一般选取方法。
2)依托杭州市富阳区金桥北路市政综合管廊基坑工程案例,对地下连续墙鲁棒性设计方法进行了研究,分析了确定性设计方法、可靠度设计方法及鲁棒性设计方法三类设计方法的区别,并进行了比较,确定了对于管廊工程地下连续墙支护体系使用鲁棒性设计方法的必要性。
本文对于综合管廊工程风险性的研究尚处于二维剖面阶段,在后续的研究中,将继续深入研究在三维基坑情况下,考虑尺寸效应、时间效应等对风险控制的影响。另外,需要对鲁棒性设计方法进行系统的研究,提出一套完整的适用于地下管廊工程的鲁棒性设计流程。
