基于CNN神经网络的煤层底板突水预测

陈建平，王春雷，王雪冬

（辽宁工程技术大学矿业学院，辽宁 阜新 123000）

0 引言

我国“相对富煤、贫油、少气、缺铀”的资源条件决定了煤炭作为我国主体能源的地位短期内不会改变[1]，随着煤层开采深度的不断增加，矿井水文地质条件日趋复杂，突水致灾因素普遍增多，煤层底板突水威胁日益严重，很多煤矿煤层底板突水预测已经成为水害防治工作的中心环节与首要任务[2]。因此，分析煤层底板突水的影响因素、准确评价突水的危险性等级，对煤矿防治水工作具有重要理论意义与实际指导作用[3]。

在煤层底板突水的预测方法中，突水系数法已列入我国《煤矿防治水手册》中，对生产实践具有指导性地位。但实践证明，突水系数法考虑的影响因素较为单一，突水系数不具有针对性[4]，不足以满足复杂的突水问题，在一些煤矿对生产的指导意义不明显。研究表明，煤层底板是否突水，取决于各类因素之间错综复杂的非线性关系[2]。大量的科研人员从不同角度出发，根据影响煤层底板突水的因素，提出了许多不同的煤层底板突水预测方法，主要有层次分析法[5]、脆弱性指数法[6]、Logistic 回归分析法[7]、专家系统[8]、地学信息复合叠置[9]、模糊证据理论[10]、贝叶斯网络[11]、Fisher 判别分析[3]、极限学习机[12]、支持向量机[13−14]和BP 神经网络[15]等，这些方法在煤层底板突水预测和实际监控中已经得到应用。上述方法均有一定的局限性，主要体现在三个方面：一是煤矿数字化的发展会挖掘出大量的基础数据，现有方法使用的数据较少，忽略了许多影响煤层底板突水的因素。二是突水影响因素之间存在的相互联系、相互影响，在预测时没有考虑；三是现有模型的计算深度已远远不足，对数据的挖掘太浅，不能更深入地分析潜在的变化规律。随着智慧矿山的发展，煤矿数字化技术越来越成熟，需要综合考虑影响煤层底板突水的多种因素及其相互关系，有效利用已有的地质参数。

卷积神经网络是常用的深度学习算法，有较高的计算深度，对数据有更深层次的挖掘，能更高效地提取出特征规律，有助于提高预测精度。卷积神经网络是人工智能领域的产物，能容纳处理更多的信息，适合煤矿数字化的发展。

1 底板突水影响因素确定

1.1 突水因素分析

研究表明[2−3]：煤层底板突水问题是以水文地质条件为背景，受到含水层、隔水层、地质构造、煤层条件以及开采方法等诸多因素的影响和控制，这些影响因素直接决定了煤层底板是否突水。

含水层是引起突水的必要条件；隔水层是抑制突水的必备条件；地质构造、煤层条件以及开采方法是影响隔水层完整性和隔水能力的主要因素。

1.2 突水因素确定

煤层底板突水是由多种因素共同作用而发生的，通过对上述突水机理的研究和分析，总结得出影响煤层底板突水的主要因素分别是：含水层、隔水层、构造、煤层、开采条件。

含水层因素决定了底板突水时水量大小以及持续涌水的时长。含水层因素主要包括含水层的富水性、水压(x2)、含水层的厚度(x3)，其中含水层的富水性通过单位涌水量(x1)来评价。

隔水层因素主要包含隔水层的厚度(x4)和隔水层的岩体基本质量(工程岩体分级标准GB/T50218-2014)，隔水层的薄厚以及岩体基本质量决定了抵抗水压和抑制突水的能力，其中岩体基本质量是岩体所固有的、影响工程岩体稳定性的最基本属性，由岩石坚硬程度和岩体完整程度确定。岩石坚硬程度的定量指标，采用岩石饱和单轴抗压强度(x5)；岩体完整程度的定量指标，采用岩体完整性指数(x6)。

构造因素包含的内容较多，但影响隔水层的完整程度的主要因素是断层、裂隙和陷落柱。由于采集到的煤矿实测资料中均未出现陷落柱，因此选取断层和裂隙作为本次评价煤层底板突水的构造影响因素。断层数据来源于煤矿实际揭露的断层(x7)，其中大断层(x8)是指落差大于20 m 的断层。裂隙发育程度(x9)是选取代表性地段的岩石裂隙率。

煤层因素主要受到自身所处位置的决定，如煤层的埋深(x10)和煤层的倾角(x11)。

开采因素主要是由开采方法、工作面布置以及底板破坏带深度(x12)构成，开采方法和工作面布置主要包含工作面长度(x13)、采高(x14)、开采面积(x15)，其中底板破坏带深度数据是采用瞬变电磁和高密度电法系统物探法现场实测得出。

通过对上述因素的分析，参考已有指标体系，结合煤矿数字化发展获得的实际数据，将煤层底板突水影响因素确定为5 项一级指标和15 项二级指标，具体数据见表1。

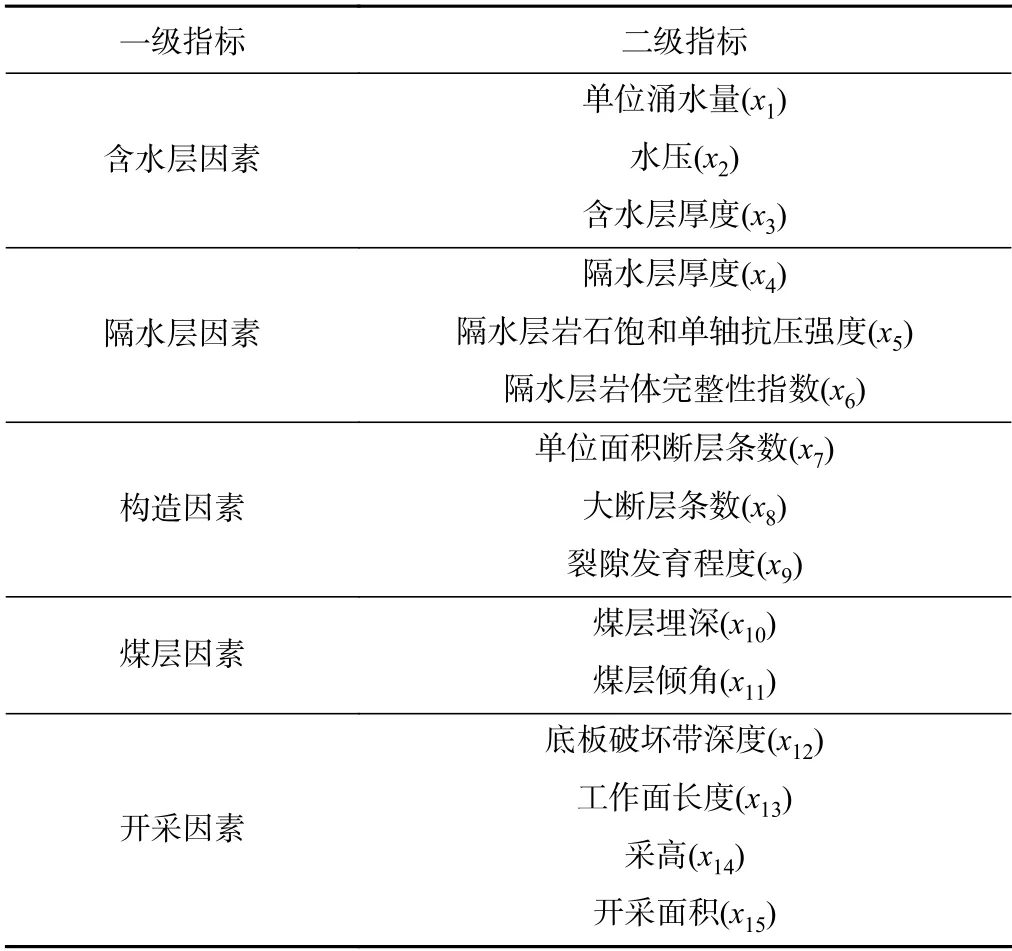
表1 影响煤层底板突水的因素Table 1 Factors affecting water inrush from coal floor

2 基于CNN 神经网络的煤层底板突水预测

2.1 卷积神经网络概述

卷积神经网络是常用的深度学习算法，能够适应信息化时代，对于信息量大的问题有较好处理能力，可以学习大量输入与输出之间的映射关系，有着较高预测精度。研究表明[16]，计算深度越深越有利于分类预测。卷积神经网络的应用非常广泛，在自然语言处理[17−18]、人脸识别[19]、医药检测[20−21]中都有应用。

卷积神经网络一般由输入层、隐藏层和输出层组成，其中隐藏层主要由卷积层、池化层和全连接层构成。卷积神经网络采用的方式是局部连接，这种连接方式与BP 神经网络相比能有效减少神经网络中的参数个数，提高计算效率，还能读取影响因素间的相互联系，增强模型的可靠性，BP 神经网络与卷积神经网络连接方式见图1。

图1 BP 神经网络与卷积神经网络连接方式示意图Fig.1 Schematic diagram of connection mode between BP neural network and convolutional neural network

卷积神经网络的核心结构是卷积层和池化层，卷积层的功能是对输入数据进行特征提取，池化层则是对提取的特征进行筛选和过滤，经过几轮卷积层和池化层的处理，模型可以提取出抽象程度更高、更符合事物变化规律的特征，就能做出更精准的预测。在卷积神经网络中，卷积层和池化层越多学习的深度越深。卷积神经网络结构示意图见图2。

图2 卷积神经网络结构示意图Fig.2 Structure diagram of convolutional neural network

2.2 模型结构确定

2.2.1 卷积层结构确定

煤层底板突水预测属于分类问题中的二分类问题，需要将样本分到突水和不突水两个类别中。直接使用较深的CNN 模型计算时间长、容易出现过拟合现象，难以取得好的效果；而使用太浅的模型往往不能有效提取因素之间的相互作用特征，导致计算精度不够，而模型的计算深度由卷积结构的多少决定，因此需要确定CNN 模型中卷积层的数量。选取模型的准确率和标准误差(SE)作为模型精度的评价指标。

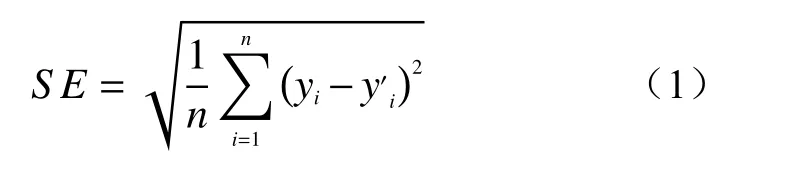
式中：n——表示数据集大小；

yi——样本实测值；

在CNN 模型中控制参数和训练次数相同，使用数量不同的卷积层对样本数据进行预测，计算结果如表2所示。对比预测结果，当卷积层数量为1 时，准确率最低，标准误差最大；卷积层数量超过2 个时，标准误差逐渐增大，选2 个卷积层时准确率最高，误差也最小，因此确定模型结构中卷积层的数量为2 个。

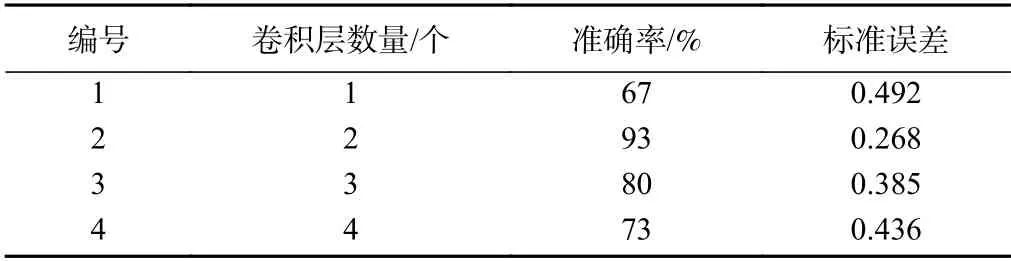
表2 不同卷积层的预测结果Table 2 Prediction results of different convolution layers

2.2.2 模型整体结构确定

CNN 模型整体结构见图3。模型共分为8 层，由左至右依次为：第一层是输入层，负责将实验数据传入模型中，考虑到模型的大小将输入层尺寸定为28×28×1；第二、四层是卷积层，深度分别为32 和64。卷积核（Kernel）大小为5×5，移动步长为1。每个卷积层后连接一个池化层，过滤器大小为2×2、移动步长为2，模型采用的是最大池化层(Max pooling)，与平均池化层相比（Average pooling），最大池化层有更高的准确性。第六、七层是全连接层，节点数分别为620 和300，在全连接层中，使用Dropout 方法[22]随机忽略一部分节点，改善模型过拟合现象。最后一层为输出层，数据通过Softmax 回归之后的交叉熵损失函数得到最终分类，输出预测值，预测值即分类概率，表示发生突水的概率，范围[0,1]。其中预测值在[0,0.5)范围表示不突水、在[0.5,1]范围表示突水。Softmax 函数和交叉熵损失函数分别为：

图3 模型结构示意图Fig.3 Schematic diagram of model structure

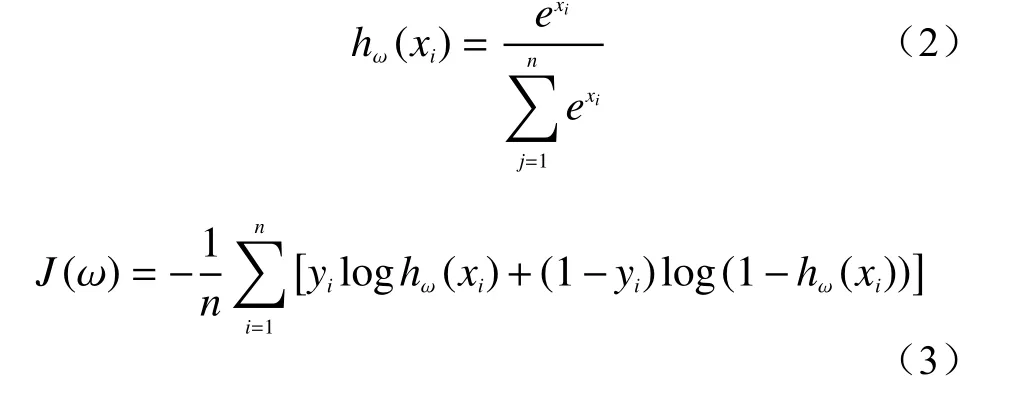
式中：J(ω)——为交叉熵损失函数；

xi——经过全连接层的输出值；

yi——表示训练集第i个数据的值，值为逻辑型数据，分两种“0”和“1”，分别表示不突水和突水；

hω(xi)——经过Softmax 回归后的值。

2.3 数据选取与预处理

2.3.1 数据来源

本文数据来源于我国华北典型矿区实测数据115 组，主要包括河北峰峰、河南鹤壁、山西霍州、山东淄博等典型矿区的工作面资料，这些矿区位于同一地区并且具有相似的水文地质特征，训练数据为100 组和测试数据为15 组，部分数据见表3。

2.3.2 数据标准化

突水影响因素具有不同的量纲和数量级，如果在模型中直接输入原始数据，在综合分析中数值相对较高因素被增强，而数值相对较低的因素则被削弱。因此，为了保证实验结果的真实性和准确性，需要对原始数据进行标准化处理，即对数据同趋势化处理和无量纲化处理。

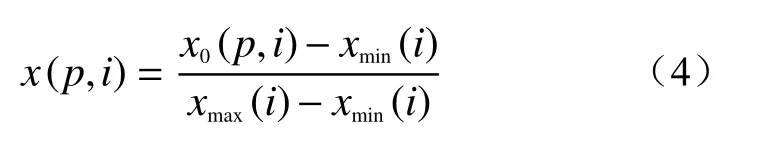
式中：x(p,i)−表示样本p中第i个因素经过归一化之后的值；

x0(p,i)−表示样本p中第个i因素的值；

xmax(i)−表示样本中第个i因素中的最大值；

xmin(i)−样本中第个i因素中的最小值。

表3 部分样本数据Table 3 Part of the sample data

2.3.3 输入数据处理

卷积神经网络可以输入一维至多维数据，一维数据与多维数据相比结构简单，表示的信息类型单一，没有多维数据信息丰富。模型在进行特征提取时，多维数据可以以组合的形式提供信息。在处理煤层底板突水问题时，往往将影响因素以单一向量输入到模型中，而没有考虑影响因素之间的相互联系。为此，本文将影响因素进行拼接，以组合的形式输入到模型中，模型内的卷积核就会在特征提取时将接触紧密的影响因素一起提取，通过不断的学习，掌握其特征规律，这种组合形式可以体现影响因素之间的相互联系。

影响因素之间的相互联系存在不确定性，无法做出具体定量，为此本文设计了随机分布法来体现影响因素之间的相互联系。具体而言，就是通过设置每个影响因素与其他影响因素在拼接组合时的接触概率来体现各个影响因素之间的相互联系。通过设置不同的接触概率，发现设置为50%时，CNN 模型在训练集的准确率最高，结合采集数据矿区的地质条件，经综合考究确定将本文各影响因素的接触概率设置为50%，计算结果见图4。

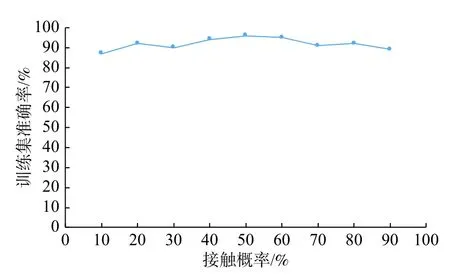
图4 接触概率设置对比实验结果Fig.4 Comparative experimental results of contact probability setting

模型输入矩阵大小为28×28，共计784 个点。组合过程大致如图5所示，将评价煤层底板突水的15 个影响因素依据接触的概率循环填入矩阵中，直到矩阵填满，整个数据拼接过程均采用Python 语言编译实现。

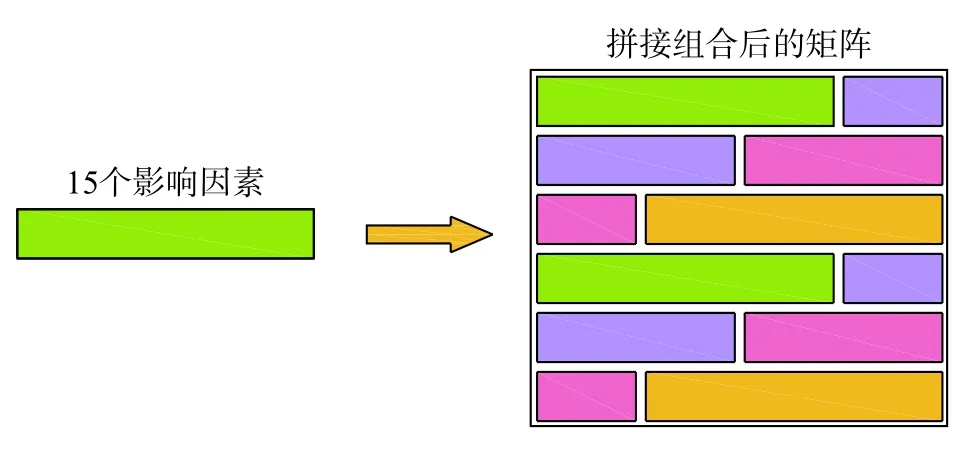
图5 数据拼接组合过程示意图Fig.5 Schematic diagram of data assembly process

2.4 模型训练

CNN 模型执行监督学习训练，训练过程分为向前传播和反向传播两个阶段。在开始训练前，先确定卷积神经网络结构，对初始参数进行设置，将拼接组合好的三维数据输入模型中，使数据向前传播，模型学习训练样本中煤层底板突水的趋势与实际值比较得到正确率，然后进行反向传播，使用优化算法更新权重矩阵，从而提高模型的正确率，根据模型实际情况确定训练次数。

2.5 模型预测实验

2.5.1 实验环境及参数设置

实验采用Python 语言编译，在开源深度学习工具TensorFlow 中采用Keras 实现卷积神经网络的煤层底板突水预测模型。在实验开始前，需要配置模型参数，卷积层中激活函数选用ReLU，输出层采用Softmax 函数和Binary cross entropy 交叉熵损失函数，优化算法选取Adam 算法[23]，影响模型预测正确率的参数还有Learning rate、Epochs、Batch size 和Dropout，具体参数值如表4所示。

表4 实验参数Table 4 Experimental parameters

Learning rate 表示学习率，主要作用是控制模型中参数更新幅度的大小，本文选用Adam 优化算法调节学习率。

Epochs 表示模型训练次数，如果正确率趋于稳定可以主动终止训练。多次实验发现模型在1 400 次左右开始趋于稳定，为防止偶然性，在模型训练1 800 次时停止训练。

Batch size 表示批量大小，即每次训练在数据集中选取的个数，其大小影响模型的优化程度和速度，该值是根据输入矩阵的尺寸和计算机内存显存大小来确定。

Dropout 是指在神经网络训练时随机忽略部分节点使其不工作，防止模型放大或者缩小某些特征，以此改善模型过拟合问题。根据以往经验Dropout 值取0.5，即每次训练随机使50%的节点不工作。

2.5.2 实验结果分析

经过训练后的CNN 模型在训练集和测试集上的准确率达分别为96%和100%。从图6中可以看出，随着训练次数逐渐增加，CNN 模型在训练集和测试集上的准确率都在不断提高，在训练次数到1 400 次左右，在测试集准确率达到100%，在模型训练1 800 次后停止训练。从图7中可以得出，CNN 模型在测试集上的预测值与实际值整体变化趋势相符合，具体数值存在差异。模型在训练集和测试集上准确率均相对较高，并且数值相差不大，再结合测试集上预测值与实际值之间的差异性，可以说明模型未出现明显的过拟合现象，模型具有较好的预测能力，较适合预测煤层底板突水问题。

图6 CNN 模型在训练集和测试集上的正确率Fig.6 The accuracy of CNN model on the training set and test set

3 对比实验

为验证模型的有效性，将本文建立的CNN 模型与BP 模型[15]和LeNet-5 模型[24]进行对比实验。采用Keras 实现BP 模型和LeNet-5 模型，在不改变模型整体架构的同时，对模型的输入层和输出层稍加修改，使其适合预测煤层底板突水问题。然后选用相同数据对煤层底板突水进行预测，选取训练集准确性、测试集准确性和测试集标准误差作为模型准确性的评价指标，对模型进行评价。

实验结果如表5、表6所示，本文建立的CNN 模型在训练集和测试集上的准确率均优于BP 模型和LeNet-5模型，并且在测试集上的标准误差最小。LeNet-5 模型和CNN 模型均采用的是卷积神经网络结构，在准确率上明显高于BP 神经网络模型。从图7中可以看出，BP 模型对测试集的预测结果不理想，且数值多分布于突水预测临界值附近。而CNN 模型和LeNet-5 模型的预测结果较好，对突水变化规律有较好的掌握，结合实验结果可以说明卷积神经网络对特征的提取更为有效，在煤层底板突水上可以做出更为精准的预测。CNN 模型和LeNet-5 模型虽然在结构相似，但计算深度不同，CNN 模型的计算深度更深，在预测上取得较高的准确率，说明本文建立的CNN 模型对数据的挖掘更深，更适用于煤层底板突水预测。

图7 测试集上的预测值与实际值对比Fig.7 Comparison of predicted and actual values on the test set

表5 各个模型的正确率Table 5 Accuracy of the predicted results

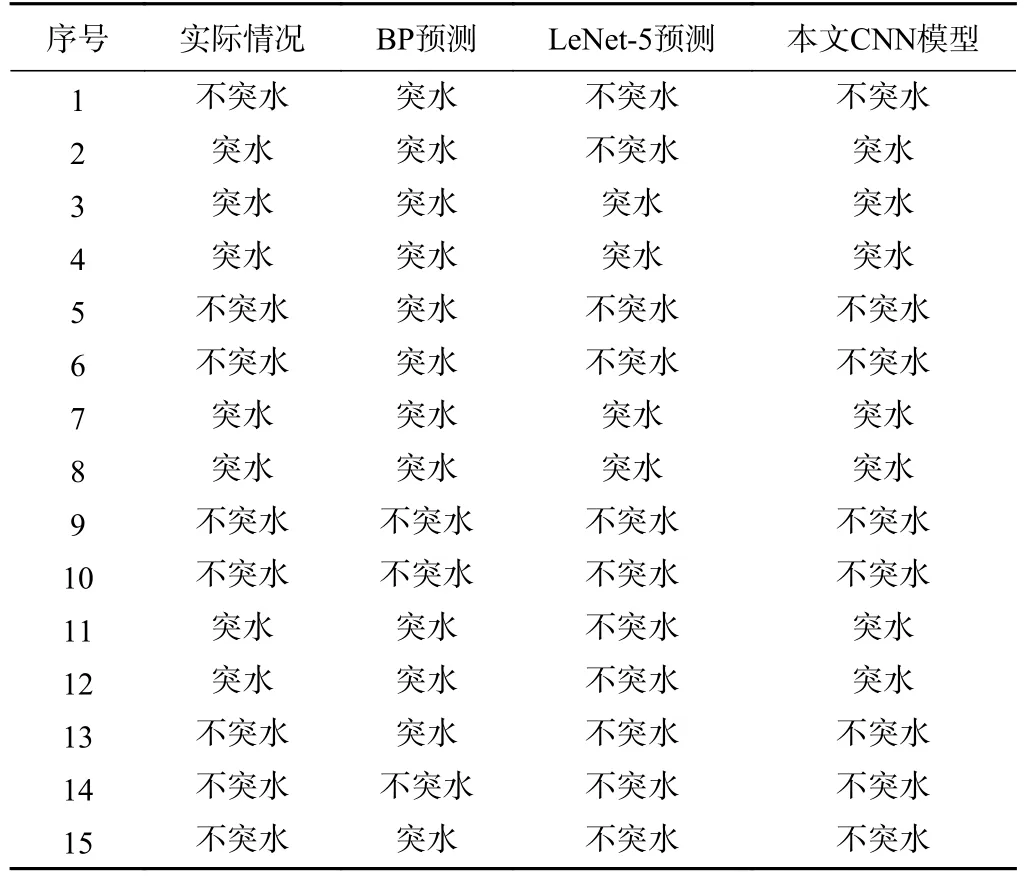
表6 各个模型的预测结果Table 6 Testresults of the forecast model

4 结论

（1）本文在分析突水机理的基础上，总结得出5 个一级指标，分别是含水层因素、隔水层因素、构造因素、煤层因素、开采因素。对上述主要影响因素进一步分析以及参照煤矿实测数据得到15 个二级指标，分别是单位涌水量、水压、含水层厚度、隔水层厚度、隔水层岩石饱和单轴抗压强度、隔水层岩体完整性指数、单位面积断层条数、大断层条数、裂隙发育程度、煤层埋深、煤层倾角、底板破坏带深度、工作面长度、采高、开采面积。

（2）本文将影响煤层底板突水的各因素进行拼接组合，以组合的形式输入到模型中，这种方式综合考虑了影响因素间的相互联系对煤层底板突水预测产生的影响。运用CNN 构建煤层底板突水预测模型对煤层底板进行预测，结果表明该模型准确率较高，从模型结构上可以说明该模型的计算深度更深，对数据的挖掘利用更充分。

（3）使用本文建立的CNN 模型与BP 模型、LeNet-5 模型进行对比实验，实验结果表明，CNN 模型的预测准确率最高，标准误差最小，说明该方法提高了预测精度，卷积神经网络可以应用于煤层底板突水预测。