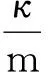基于GeoGebra对一种弹簧摆问题的可视化研究

陈林 桑芝芳

(苏州大学物理科学与技术学院 江苏 苏州 215000)

1 试题及解析

如图1所示，一轻质弹簧固定于C点，另一端固定一小球，将小球从与悬点C在同一水平面且弹簧保持原长的A点无初速度释放，让其自由摆下，不计空气阻力，在小球摆向最低点P的过程中，下列说法中正确的是( )

A.小球的重力势能减少

B.小球的机械能减少

C.小球的重力势能与弹簧的弹性势能之和不变

D.小球与弹簧组成的系统机械能减少

图1 试题情境图

解析：小球从A运动到P的过程中，以小球为研究对象，重力做正功，重力势能减小，选项A正确；但是由于弹簧弹力做负功，将小球的一部分机械能转化为弹簧的弹性势能，所以小球的机械能减少，选项B正确；此过程重力势能减少，转化为弹簧的弹性势能和小球的动能，所以小球的重力势能与弹簧的弹性势能之和减小，选项C错误；只有重力和弹簧弹力做功，所以系统机械能守恒，选项D错误．本题答案为选项A，B．

以上分析是定性分析，纵使能把答案选出来，学生依然会有许多疑问：

(1)小球接下来的运动轨迹是怎么样的？

(2)悬点正下方P点，小球速度的方向是水平吗？

(3)小球的合速度大小是怎么变化的？能画出速度图像吗？

(4)P点合力方向向上还是向下？

……

关于疑问(3)，文献[1]作者通过MATHCAD给出结论：在一个周期内小球合速度先变大再减小，然后变大最后减小．

关于疑问(4)，文献[2]作者通过动力学方程分析出P点合力方向向上．

通过查阅更多文献，发现对该弹簧摆研究内容不少，但大多是面对大学层次学生的教授，通过MATLAB，MATHEMATICA，MATHCAD等软件进行数值模拟，或者是如文献[2]通过实验进行探究．但MATLAB，MATHEMATICA，MATHCAD等软件对中学教师来说使用难度较大，GeoGebra软件不仅使用简单，无需编程，而且同样可以进行数值模拟，对中学物理教学有很大帮助．

接下来，本文针对疑问(1)、(2)，借助GeoGebra软件进行探究．

2 建立模型

以弹簧悬挂点为原点建立如图2所示的坐标系，图2所示为任意时刻小球所在的位置P(x,y)．开始时θ=90°，小球处于水平位置，弹簧处于原长L0，设弹簧劲度系数为κ，小球质量为m．

图2 建立坐标系

2.1 微分动力学方程

对小球分别进行水平方向和竖直方向上的受力分析.

在水平方向上有

(1)

在竖直方向上有

(2)

其中

整理可得,水平方向

(3)

竖直方向

(4)

x(0)=L0y(0)=0

2.2 GeoGebra数值模拟

实际上，不同的初始摆角、劲度系数、小球的质量、弹簧的原长等都会影响弹簧摆的运动规律[3]．本文由题意知，小球是从水平位置下落，所以初始条件设为θ=90°．为方便起见，不妨设弹簧原长

L0=20 mg=10 m/s2

κ=1 N/mm=0.01 kg

用GeoGebra描绘小球运动轨迹如图3所示，小球的速度与水平位移的关系图如图4所示，小球重力势能、弹性势能、动能与水平位移关系图如图5所示，B，D，C3条线分别代表重力势能、弹性势能、动能．图6则是任意时刻小球的重力势能、弹性势能与动能具体数值，可以看出三者能量守恒，总和为零．

t=50 s；L0=20 m；

图4 速度和水平位移的关系图

图5 小球重力势能、弹性势能、动能与水平位移关系图

图6 任意时刻小球的重力势能、弹性势能与动能

2.3 图形分析

2.3.1 轨迹图

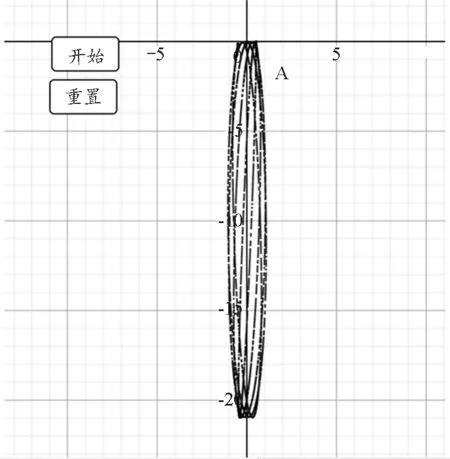
在L0=20 m，κ=1 N/m，m=0.01 kg时，图3是该弹簧摆的运动轨迹图，其轨迹近似是半个圆周，在悬点正下方小球的速度是水平的．

2.3.2 速度与水平位移关系图

由图4可知，从下落开始，小球的速度先增大后减小，最低点速度达到最大，且呈周期性变化．

2.3.3 重力势能、弹性势能、动能与水平位移关系图

由图5可以看出，小球从下落开始，在一个周期内，重力势能先变小后变大，弹性势能先变大后变小，动能先变大后变小．整个系统能量守恒，不过弹性势能对整个系统影响较小．

2.4 拓展分析

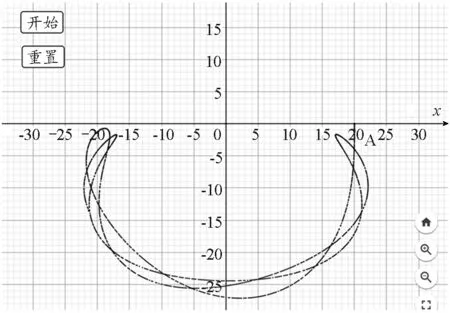
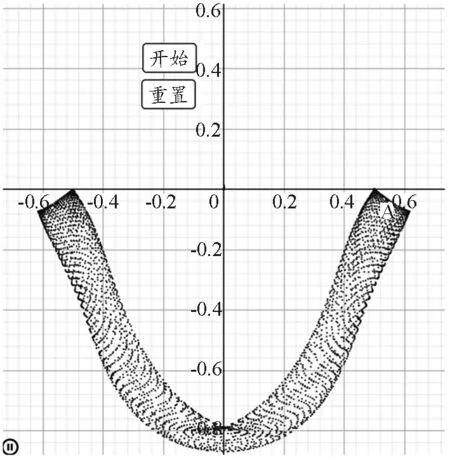
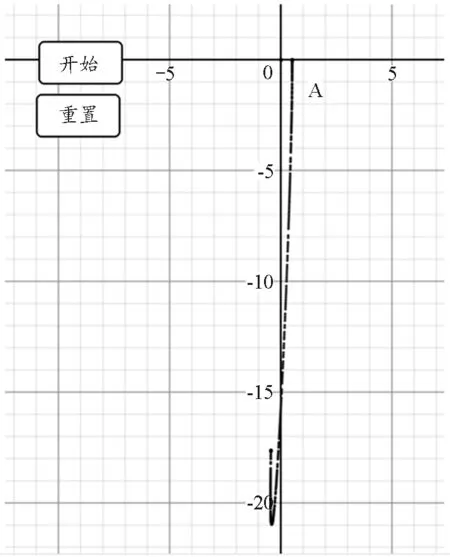
此外，在三维模型中，若给小球一个y轴方向的初速度，设

运动轨迹如图10所示.由图可以看出，小球的运动轨迹像一朵盛开的莲花，从而更能体现出弹簧摆问题的复杂性与多样性．

图10 在三维模型中小球运动轨迹像莲花

3 结论与反思