朱隈水库汛期水位动态控制研究

华 昆

(庄河市水务事务服务中心，辽宁 大连 116400)

1 工程概况

朱隈水库位于庄河市太平岭乡庄河的西支流上，是一座集防洪、灌溉、城市供水、发电和养鱼等综合利用功能的大(2)型水库，总库容16 562万m3，防洪限制水位42.94 m，正常高水位43.26 m，控制流域面积260 km2，设计灌溉面积9300 hm2，为多年调节水库。水库设计和校核洪水标准为100年一遇、1000年一遇，主要由溢洪道、主副坝、发电厂房及引水隧洞组成。其中，主、副坝为黏土心墙坝和复合土工膜面板坝，主坝最高19.5 m、长达340 m，副坝在强风化岩体上铺设复合土工膜并浇筑面板保护层。受独特的地貌形态和气候环境影响，朱隈水库所在流域降水时空分布极不均衡，水资源供需矛盾、季节性缺水以及旱涝灾害交替等问题突出，迫切需要利用洪水资源。考虑到多属性、多目标的汛期水位动态控制因素，对朱隈水库汛期水位动态控制决策方案是利用基于权重搜索技术的VIKOR模型进行分析[1-3]。通过动态控制汛期水位，在保证防洪安全的情况下尽量提升水库的运行水位，对提升朱隈水库的兴利效应发挥着巨大作用。

2 水位动态控制模型

2.1 改进云模型赋权法

借鉴文献[4]建模流程，计算数字特征向量在两个云模型的相似度是其关键步骤，利用式(1)计算传统云模型相似度Cs(i,j)，即：

(1)

从式(1)可知，传统云模型的相似度忽略了模长，运算过程中仅考虑向量方向的相似度。针对此问题，本文考虑综合相似度D(i,j)利用模长相似度和方向相似度确定，其表达式为：

D(i,j)=Cs(i,j)d(i,j)=

(2)

从式(2)看出，综合相似度D(i,j)可以更加全面的获取计算结果，在不同方案中综合相似度具有更大的区分度，为后续的比较提供可靠依据。总体而言，在主观赋权中应用改进云模型的流程如下：(1)打分准则的合理设置。按照重要、比较重要、一般、比较不重要、不重要五个等级评判指标的重要程度，为便于专家打分设置各等级的打分准则依次为：(8,10]、(6,8]、(4,6]、(2,4]、(0,2]。(2)生成准则云图。对于参评因子1,2,…,j,…,m邀请权重相同的n位专家打分，从而形成相应的打分向量为Tn=(T1n,T2n,…,Tjn,…,Tm n)，考虑所有专家的打分构造综合向量为T=(T1,T2,…,Tj,…,Tm)，然后生成各参评因子的综合打分云图和评价准则云图。(3)确定主观权重，将每个参评因子的综合相似度Dj代入式(3)求解相应的主观权重ωj1，即：

(3)

2.2 Critic客观赋权法

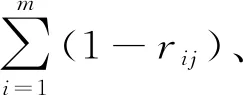
(4)

信息量Cj值越大则权重越高，并利用式(5)求解权重：

(5)

2.3 基于差分算法的权重搜索

实质上，在搜索空间内有机结合主客观权重信息就是基于差分算法的权重搜索技术，将综合权重利用差分算法寻优确定，能够更加符合客观实际。实际应用时具有原理清晰、操作灵活等特点，可为多因素、多目标赋权决策问题提供一种新的思路，其主要流程如下。

(1)对参评因素j的主、客观权重利用改进云模型和Critic赋权法计算，即获取权重ωj1、ωj2，结合实际情况生成权重搜索上、下限空间，如式(6)和式(7)

(6)

(7)

(2)在方案1、方案2、…、方案n地位平等且VIKOR法Q值越小越优的情况下，构造的目标函数及其约束条件如式(8)和式(9)：

(8)

(9)

式中：Qi、Ri、Si分别为效益比率、个别遗憾和群体效益；S+=max{Si}；S-=min{Si}；R+=max{Ri}；R-=min{Ri}。v为决策机制系数，v>0.5、v<0.5、v=0.5分别代表决策者偏好最大化群体效益、最小化个别遗憾和选择折中的决策方式。

(3)采用差分算法对以上运算结果寻优，从而获取耦合了主、客观权重的综合权重ωj。

2.4 VIKOR动态决策模型

VIKOR决策模型如式(10)～式(12)：

(10)

(11)

(12)

依据准则1、准则2分析决策结果，在满足评判准则的条件下确定最优妥协解。准则1：以Q2-Q1≥1/(n-1)作为优势度可接受判断准则，其中n为决策方案数，Q2、Q1为次优和最优方案的评价值。准则2：以最优方案S或R的排序作为决策可靠性接受准则。在两个准则同时满足的情况下，Q值最小方案即为最优方案；若不符合准则1，则获取一组满足条件Qk-Q1<1/(n-1)的最优妥协解，即F(1),F(2),…,F(k)；若不符合准则2，则最优妥协解为确定的次优和最优方案。

3 实例应用

对朱隈水库汛期运行水位动态控制方案是利用VIKOR决策模型和权重搜索技术进行分析，水位动态控制决策方案集如表1。

考虑朱隈水库的实际利用情况，选择6项代表性评价指标，由此构造方案集的初始评价矩阵F′，如表2。

表1 朱隈水库水位动态控制决策方案集

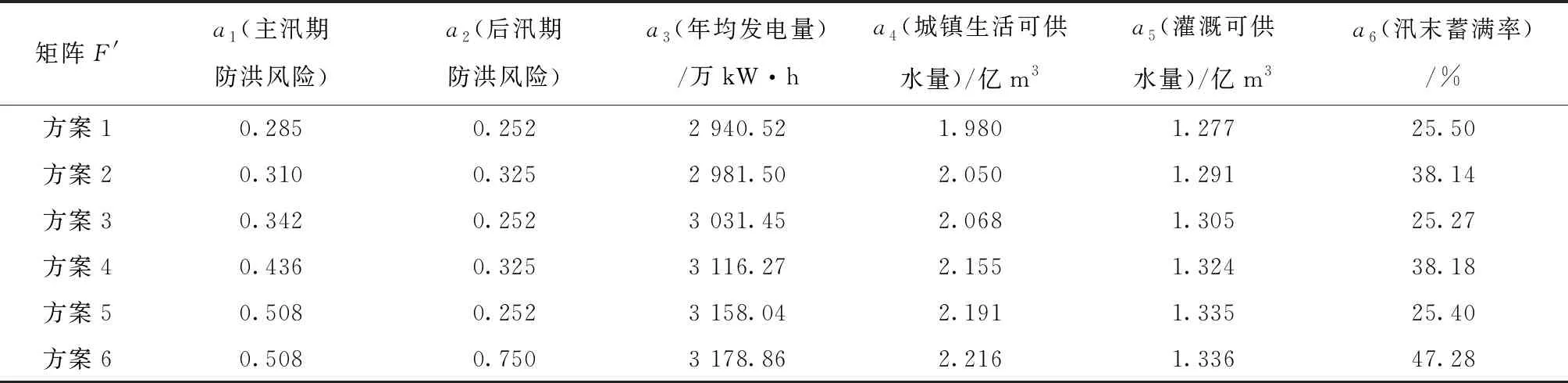
表2 方案集初始评价矩阵F′

其中，结合防洪风险损失和防洪风险率确定防洪综合风险，即考虑分洪水量期望值r2和极限风险率r1计算综合风险，典型洪水过程的选择遵循主峰靠后、峰高量大的原则；针对不同频率下的设计洪水过程线利用频率分析法确定，通过调洪演算各频率下起调水位的洪水，可以获取相应的调洪最高水位；将分洪水量期望值、极限风险率利用最高调洪水位与频率关系曲线确定，其关系式如式(13)～式(14)：

Pf=P{Zm=Zg}

(13)

(14)

式中：Pf、Pi为极限风险率和洪水频率；W0、Wi为分洪水量期望值和Pi对应的分洪水量；n、i为参与计算的洪水场次数和洪水频率顺序排列序号；Zg为水库防洪高水位。朱隈水库承担着保护下游重要基础设施、农田和沿河乡镇安全，以及控制庄河洪水和下游防洪的任务。采用以下公式规范化分洪水量期望值和极限风险率，如式(15)：

(15)

在此基础上可以确定防洪综合风险，即：a1=ξ1Rf1+ξ2Rs1、a2=η1Rf2+η2Rs2；其中，Rf1、Rs1为主汛期的规范化防洪风险率和标准化防洪风险损失；Rf2、Rs2为后汛期的规范化防洪风险率和标准化防洪风险损失；ξ1、ξ2、η1、η2为权重系数，文中取0.5。

将初始评价矩阵F′利用标准化公式进行处理，从而得到标准决策矩阵F，结果如下：

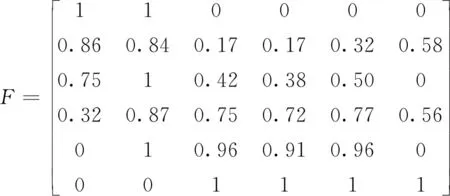
依据各项参评因素的具体内涵和标准化决策矩阵F，生成正、负理想方案F+={1,1,1,1,1,1}和F-={0,0,0,0,0,0}。然后确定主客观权重w1={0.220,0.185,0.171,0.201,0.117,0.106}、w2={0.180,0.155,0.168,0.164,0.161,0.172}，并生成权重搜索空间的上、下限，从而获取w+={0.220,0.185,0.171,0.201,0.161,0.172}、w-={0.180, 0.155,0.168,0.164,0.117,0.106}，运用VIKOR决策模型和权重搜索技术，基于公式(8)、式(9)求解出综合权重w={0.212,0.186,0.170,0.181,0.140,0.111}。

各方案的个别遗憾R和群体效益S利用式(10)～式(12)进行计算，决策者偏好最大化群体效益、折中处理、最小化个别遗憾心理的效益比率Q分别选用决策机制系数v取0.9、0.5、0.1表征。通过以上运算处理，对每个决策方案的效益比率Q、个别遗憾R和群体效益S排序，如表3。

表3 决策方案排序

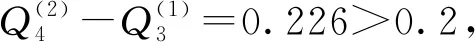
若决策机制系数v=0.1，代表各方案中较差的指标值引起决策者的特别关注，由于方案4不存在最劣、最优指标值，而方案3出现汛末蓄满率和后汛期综合风险的最劣、最优值，该情况与偏好个别遗憾的决策心理相符，所以最优妥协解为方案3；若决策机制系数v=0.5，代表决策者持中立态度，依据Q值排序方案4略优于方案3，但其并不符合优势度可接受准则，因此最优妥协解为方案3、4；若决策机制系数v=0.9，代表整体效益更引起决策者的关注，注重个别较差指标的程度减弱，从指标增幅比的角度分析，方案4存在可接受范围内的主汛期、后汛期综合风险增幅，较方案3其汛末蓄满率、灌溉水量、城镇生活可供水量和多年平均发电量增幅依次为50.2%、1.5%、4.2%、2.5%，所以从效益与风险均衡的层面，方案4更符合决策者此时心理，应作为该条件下的最优妥协解。

综上分析，在朱隈水库中应用优化的VIKOR决策模型，能够在一定程度上转变洪水资源利用率较低的现状，汛期决策者对某较差指标的特别关注可通过设置决策机制系数v来实现，实际应用时其普适性及灵活性更好[5-7]。

4 结 论

本文将传统的云模型相似度与模长相似度相结合，对主客观权重在搜索域内利用差分算法耦合，并考虑客观数据特点与专家经验确定综合权重，然后运用VIKOR决策模型和权重搜索技术进行实例分析。结果发现，VIKOR模型能够综合考虑群体效益和决策者不同的心理偏好，通过方案排序和引入特别关注的较差指标，可为动态控制汛期运行水位提供科学的决策依据。