具有时滞和动力学边界的黏弹性波方程解的稳定性

张亚静，刘玉春

（山西大学 数学科学学院，山西 太原 030006）

0 引言

本文研究如下黏弹性波方程的初边值问题，

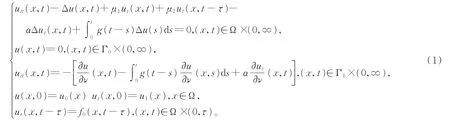
其中Ω是RN(N≥1)中的正则有界区域，∂Ω＝Γ0∪Γ1，meas(Γ0)＞0，，α和μ1是正数，μ2是实数，τ＞0表示时滞，初值(u0，u1，f0)在一个合适的函数空间中。时滞现象近年来备受关注［1—4］，它广泛存在于物理学、化学、生物学等领域。众所周知，在无时滞作用的系统中，可以得到一个稳定性结果［5—6］。在有时滞的系统中，时滞的存在是导致系统不稳定的一个因素，因此需要添加条件来保证原系统的稳定性［7］。

关于如下具有时滞的波方程的初边值问题

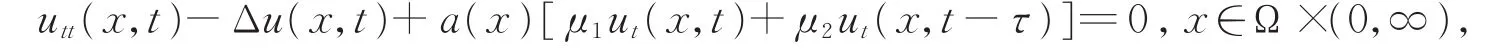
在无时滞(μ2＝0)时，系统是指数稳定的［8］，在时滞存在(μ2≠0)时，文献［9］证明了在μ1＞μ2时能量是指数稳定的，在μ1≤μ2时会存在一个任意小的时间滞后导致不稳定发生。

受以上文献启发，我们研究具有时滞，强阻尼和动力学边界条件的黏弹性波方程解的稳定性。第1节给出一些假设，准备工作和主要结论，第2节给出引理和主要结论的证明。

1 准备工作和主要结论

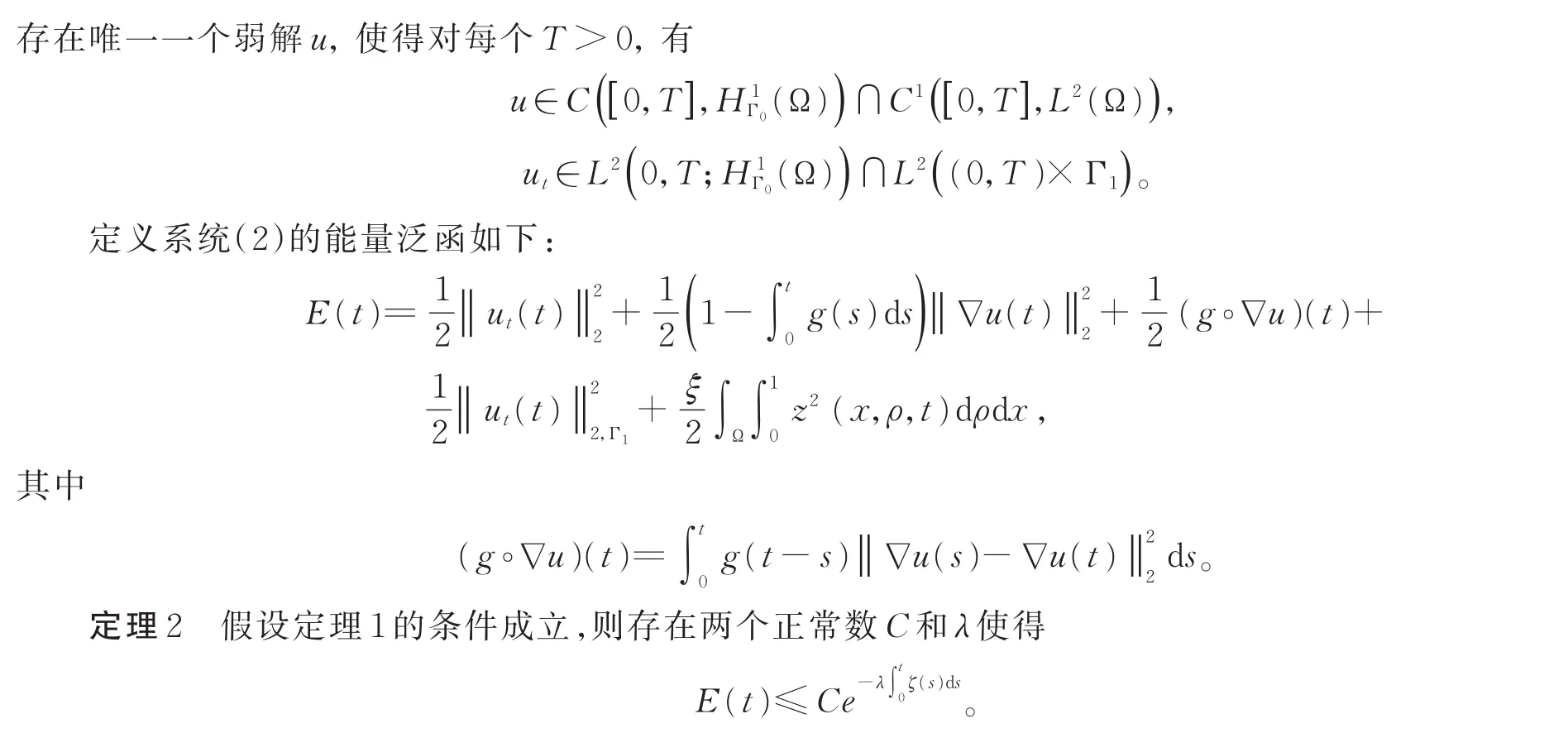
2 主要结论的证明