一种卫星对地观测需求分析方法
2021-03-03马东锋
马东锋
(1 南京理工大学 计算机科学与工程学院,南京 210094)(2 钱学森空间技术实验室,北京 100094)
随着我国航天事业的发展,对地观测卫星种类和数量日趋增多,形成了陆地观测、海洋观测、环境监测、大气和气象探测等不同遥感应用卫星领域。依据不同时期的卫星技术发展水平,准确把握卫星观测用户需求,合理统筹共性需求和专用需求,是航天器体系设计,如高分专项和空间基础设施体系等顶层规划设计的关键环节,也是规划的依据和输入。卫星对地观测的需求来自不同行业应用,对观测要素和能力指标要求复杂多样,包含多维异构信息,空域时域频域覆盖宽广,存在冗余、重叠、交叉等现象。在实际工作中,需求统筹是一项艰难和复杂的工作,迫切需要建立和改进需求分析方法和流程,对需求进行分析和管理,找出需求之间、需求与观测要素之间、要素与指标之间的关系,为卫星体系方案设计的科学性与合理性提供定量化数据支持。文献[1]通过最优化理论给出约束满足模型,并给出对应的求解方法。文献[2]基于图论理论,把需求作为顶点,约束作为边集建立图模型,并利用图论领域的算法求解。最近,文献[3]创新地提出基于数据科学的需求分析模型,通过把原始的基于文本的需求转化成数值模型,从而利用数据科学的相关算法完成对原始需求的分类分析和可视化等操作。借鉴这一思想,本文在以模板的形式结构化描述的用户需求之上,基于无监督学习[4]框架,进一步建立需求分析模型,实现对需求的快速聚类,低维直观显示,为后续体系效能评估提供新的数据支撑。
1 文本需求向量化编码
对地观测卫星系统的需求分析活动过程如图1所示。
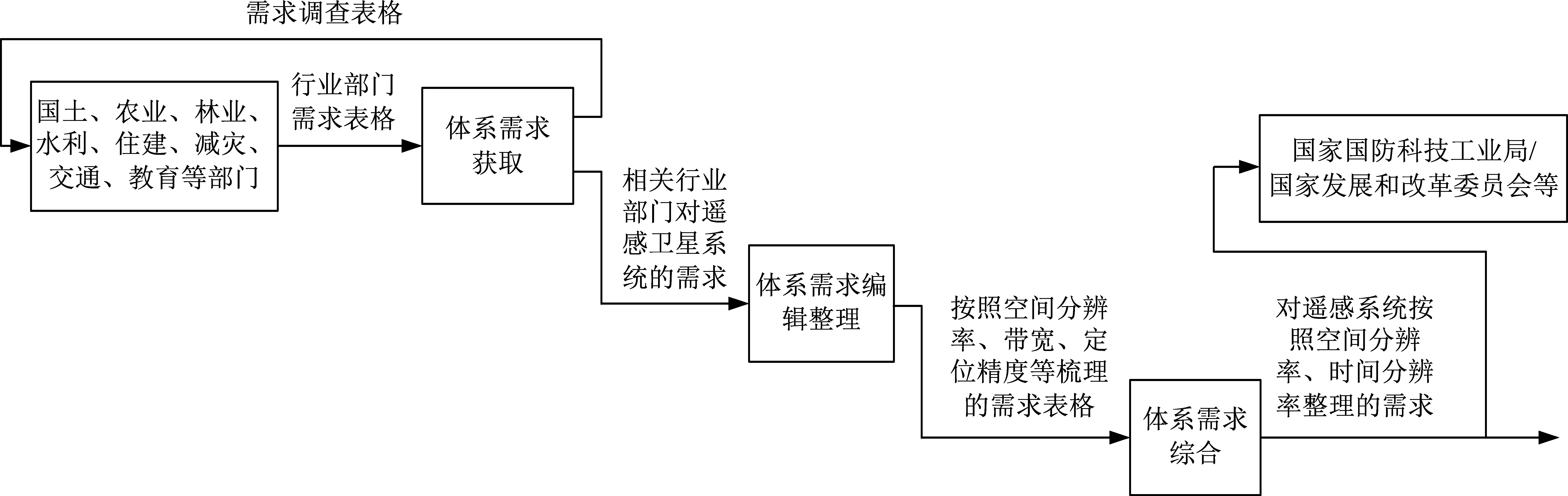
图1 “体系需求获取与综合”活动Fig.1 Acquisition and integration of system requirements
需求分析论证分为需求汇总、优化统筹、综合分析等3个阶段10个步骤,如图2所示。
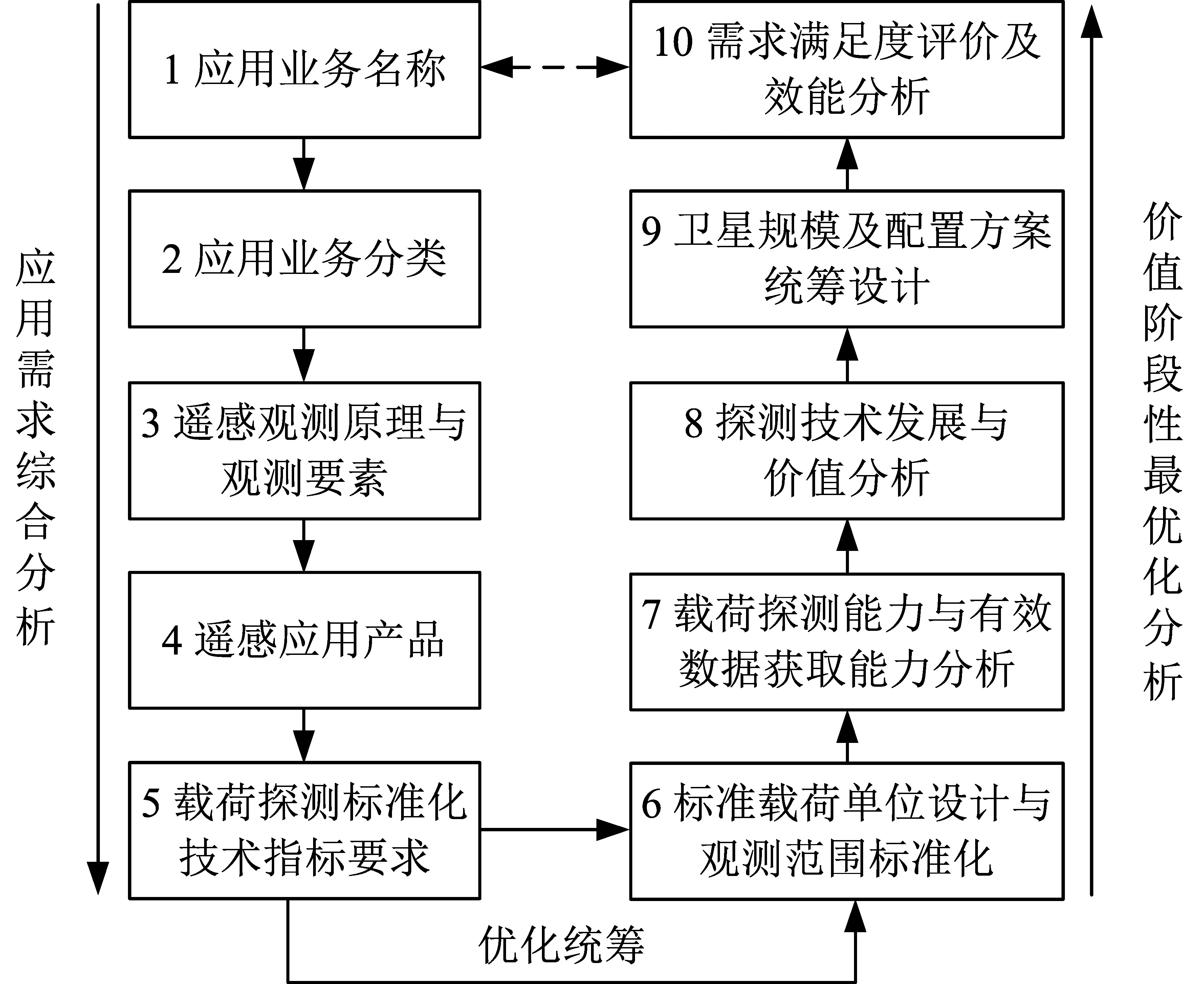
图2 卫星遥感基础设施需求分析方法Fig.2 Method of satellite observation requirements analysis
需求分析的难点在于需要考虑很多维度,针对所有遥感应用部门的观测任务需求,按照部门、业务方向、应用模式、观测要素、谱段特征、空间分辨率、时间分辨率、全球探测需求和全天时全天候探测等维度进行汇总。在多个业务部门的观测要素中,存在着重叠现象,即多部门均需要某个观测要素,这就需要在国家层面上整合对地观测的需求。
需求汇总后,通过分析提炼,得到时间特性、空间特性、谱段特性、辐射特性和精度等要素。其中,谱段特性结合空间特性用于指导卫星有效载荷的种类配置;空间特性可以指导有效载荷系统设计和卫星的轨道设计;时间特性可以指导有效载荷的观测幅宽设计和机动观测能力,如果单台载荷不能满足时间特性,还需要多颗卫星进行综合设计,得到星座或者编队飞行的设计;辐射特性可以进一步约束载荷的设计,使得载荷设计指标能够满足用于定量化应用的需求。
实践中,需求的要素更为复杂,仅观测属性就有多种类型,如:全色、紫外、可见近红外、短波红外多光谱、中、热红外、高光谱、超光谱;不同频段合成孔径雷达(SAR);微波辐射计;激光、微光、荧光;电磁、重力载荷数据等。
其中,需求不仅需要分类、还需要层次化建模,分类越清晰,对需求的描述越准确、越容易归集和规范化。通过对不同种类,不同使命任务的卫星系统进行需求分类、分层和归集,有利于对同类系统进行需求的模型化和定量化表述,有利于合理布局陆地观测系统、海洋观测系统、大气观测系统、地球物理场探测系统。限于篇幅不再展开。
体系需求综合中主要存在两个困难:一是不同应用需求属性的综合统筹;二是技术指标的多维度特征的综合,如将空间分辨率、时间分辨率和光谱范围3个指标一体化综合难度较大,常采取的策略是分割成3个独立的维度综合,使综合结果出现对原始需求的放大或缩小,但仍然没达到统筹的要求。
观测需求的维度,主要包含空间属性和观测属性(观测载荷、空间分辨率、光谱分辨率、时间分辨率、定位精度等),可以提炼和建立基本需求模型,如图3所示。

图3 需求编码模型示例Fig.3 An example of requirement coding model
实际工作中,需求大部分是文本,隐含的数据相当复杂多样,受专业人员的认识水平所限,依靠大量人工分析,将无法满足统筹的科学性和合理性。本文研究提出,借鉴人工智能领域技术,把文本描述的繁杂需求转化成向量化表示的数值数据,进行数值化需求分析,可以有效地解决需求的定量化建模和统筹。
观测任务和需求要素十分复杂,为便于表达,抽象于具体的物理意义,本文给出一种通用的文本需求编码方法。对卫星观测任务的需求,可以表示为表1的形式:其中,某一行表示某个具体的需求,可以来自于不同观测任务、不同部门、不同行业等。某一列表示该行需求对具体指标的要求,例如对空间分辨率、时间分辨率、谱段特征等的具体要求。以空间分辨率指标为例,需求1对指标的要求为0.1 m,需求2为1 m,综合需求的分布情形,可以把空间分辨率特征做如表2的划分,其中[·,·)表示左闭右开区间。该划分只是基于当前数据的剖分,目的是让每个需求对该指标的要求只落在其中一个区间,不具有实质的物理含义。比如表1中的需求1,对空间分辨率的要求只对应第一个区间,也就是说该需求只对第一个区间有要求,对其他区间无要求。因此需求1对空间分辨率的要求可以向量化表示为{1,0,0,0,0,0,0,0},如表3所示。需要强调的是,如何划分指标区间,对模型不产生本质影响。

表1 需求集合Table 1 Set of requirements

表2 空间分辨率划分Table 2 Division of spatial resolution

表3 需求1空间分辨率的向量化表示Table 3 Vectorized representation of spatial resolution for requirement 1
同样地,可以对其他指标(时间分辨率,谱段特征等)进行同样的划分操作,从而把每一条需求转化成一个只包含0,1的向量,0表示对该指标区间无要求,1反之。如此就可以把自然语言表示的文本需求进行向量化编码。
2 高维需求向量聚类分析
对需求的分类常见的方式是按照需求提出的部门或者观测任务类型归类,例如海洋环境监测领域的需求可以归为一类。但是,这种分类方式是基于先验知识,不能客观反映数据间的内在关联性。在人工智能领域,无监督学习能利用数据的隐含特征对数据进行分类,从而发掘数据中平常不容易获取的信息,在高维数据中,这种现象更为明显。为了能够利用无监督学习算法进行需求的聚类分析,首先要解决如何描述需求之间的相似性度量问题。两个需求关联程度越高,那么相似性度量结果越大,反之需求之间关联程度小,那么相似性也越小。结合这一特性,可以采用杰卡德相似系数[5](Jaccard index)刻画需求之间的相似程度。具体计算方法如下,记两个编码后的需求向量分别为a,b,相似性为s(a,b),则
(1)
式中:|a∩b|表示a,b向量对应分量同时为1的分量个数,|a∪b|表示a,b向量对应分量至少有一个为1的分量个数。不难得出,s(a,b)∈[0,1],并且值越大,向量间相似性越高。
有了向量间的相似性度量之后,就可以通过需求间相似程度进行分类,使得同一类的需求相似程度高,不同类的需求相似程度低。相较于传统的K-Means聚类算法[6],谱聚类[7]算法对数据分布的适应性更强,不仅容易实现而且聚类效果也优于K-Means算法。因此,本文采用谱聚类的算法对需求向量进行聚类分析,下面介绍详细的算法步骤。
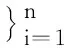
(2)算法输出:聚类结果R1,R2,…,Rk;
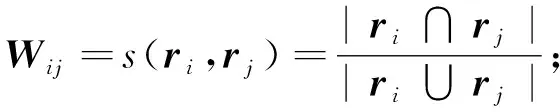
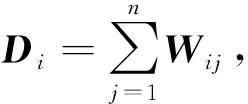
即度矩阵是由相似矩阵的每一行元素之和构成的n×n的对角矩阵;
步骤三:求出拉普拉斯矩阵L=D-W;
步骤四:计算标准化的拉普拉斯矩阵Lstd=D-1/2LD-1/2;
步骤五:求解标准化拉普拉斯矩阵Lstd的特征值,把特征值递增排序,并且记前k个特征值对应的特征向量分别为μ1,μ2,…,μk;
步骤六:通过前面得到的k个列向量构造矩阵U∈Rn*k,也就是说该矩阵的列是由特征值递增排序之后对应的特征向量组成,即U={μ1,μ2,…,μk};
步骤七:取U的第i行的行向量,记为vi,并依次把vi单位化,使得‖vi‖=1,进而构造新的向量集合V={v1,v2,…,vn};
步骤八:利用K-Means算法把V聚类分为k类,进而得到聚类结果R1,R2,…,Rk。
3 高维需求向量降维分析
信息维度高是卫星观测需求的一个显著特征,为了能够直观感受、分析需求数据,需要把需求从高维空间降维到我们熟知的2维或3维空间。自然界中同一类别的高维数据,往往集中在某个低维流形附近,这是数据科学中的基本假设[8]。在高维数据降维过程中,首先需要明确如何度量高维空间中需求向量之间的距离。前面介绍了需求向量相似性的计算方法,两个向量相似程度越高,它们之间的距离越短,反之也成立。因此对向量化表示之后的两个需求a,b,它们之间的距离可以定义如下
d(a,b)=1-s(a,b).
(2)
t分布随机近邻嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)[9]算法是目前非常流行的一种非线性的高维数据降维算法。本文基于t-SNE算法实现高维需求数据在二维平面的可视化,具体流程如下。
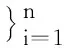
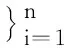
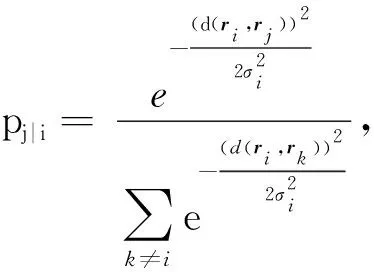
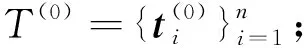
步骤四:初始化迭代次数y=1;


步骤八:y=y+1,如果y 根据文献[3]中提到的需求分析数据,经过向量化编码的数据见表4。 表4 测试数据Table 4 Test data 对该组需求数据基于本文给出的谱聚类和t-SNE算法进行聚类和降维分析,结果如图4所示。 图4 聚类和降维结果Fig.4 Result of clustering and dimensionality reduction 从图4可以看出,高维的需求数据经过t-SNE算法之后被成功绘制在二维平面。四边形、五角星、圆形3种形状代表不同的聚类结果。从图4中观察可知,同一类别的点距离较近,不同类别的点距离较远,原始数据需求被分为3类。需要指出的是由于实际情况限制,该示例只是对算法的演示,虽不具备物理解释含义,但是能够检验上述模型和算法的可行性和有效性,可以在需求分析中实现具体的物理意义。本方法在国家民用空间基础设施中长期发展规划论证中得到了实际应用,大大提高了需求分析的效率和合理性,适用于各类应用卫星特别是对地观测卫星体系规划与顶层设计。 针对复杂的卫星观测需求,本文给出了一种把文本描述的需求进行向量化表示的编码方式,同时定义了需求向量的相似度和距离计算方式。之后,在向量化表示的需求基础之上建立聚类和降维模型,同时通过测试数据演示了聚类和降维分析的结果。通过可视化的结果,说明了在向量化编码需求之后,可以在机器学习的框架之下对卫星观测需求进行各类分析,为后续基于数据科学的卫星效能评估提供基础。本文通过把繁杂的需求信息转换成高维空间向量,能大大降低分析人员对领域专业知识的过度依赖,提升需求分析的效率和科学性。4 卫星观测需求分析实例


5 结束语
