基于冻结磁导率的变压器漏感计算

张怀亮，操桃秀，齐 悦

（1.海装装备项目管理中心，北京 100000；2.中国舰船研究设计中心，湖北 武汉 430064）

0 引言

变压器漏感是分析变压器运行的重要参数，对分析变压器的性能以及应用有着重要的作用[1]。在变压器的设计过程中，工程师往往需要对变压器的漏感进行仿真估算[2-3]；近几年来，在一些新的变压器保护理论中，如等值电路参数法[3-4]、磁通特性判别法[5]、功率差动原理及基于变压器的回路方程法中也需要已知变压器各绕组的漏感[6-7]。在已有的研究中，研究者们多注重于计算变压器的短路电抗，然而短路电抗是原、副边绕组漏感之和，无法精确确定各绕组漏感的具体值。

文中通过运用有限元数值分析方法和直接耦合法同时求解电磁场和电路方程，建立了变压器的三维场-路耦合模型。运用冻结磁导率的方法计算了变压器的自感互感矩阵，再由自感互感矩阵计算得到了变压器的漏感参数。该方法从变压器的几何结构出发，能充分考虑变压器的制造工艺、结构特征以及连接组别等因素。

1 场-路耦合计算原理

1.1 场域控制方程

三维涡流场的计算主要可以分为矢量磁位A法和标量电位T法两大类[8-10]。T法（其中典型的为T φφ法）虽然未知数少，求解效率高；但在场-路耦合计算中，T法与电压项耦合比较复杂；当模型中含有铁磁材料时，T法计算的误差也较大，这也使介质参数磁导率μ的迭代很难收敛[8]；然而在变压器内部短路过程中，铁心局部区域会进入饱和，这反而降低了求解速度。矢量磁位A法在场-路耦合计算中易与引入的电压项耦合，对含有铁磁材料的模型计算精度较高。由以上分析可见，矢量磁位A法比较适合变压器的场-路耦合计算，故文中引入矢量磁位A，忽略铁心叠片涡流效应，根据Maxwell方程组可得三维非线性磁场的控制方程[11]。

上式中：μ为磁导率，H/m。

变压器在实际运行中，磁力线一般不会或只有极微小部分会穿出变压器的油箱。文中以变压器油箱为整体求解场域，在计算过程中假设变压器磁力线不会超过求解域，即边界上磁感应强度的法向分量为零，数学表达式如下所示。

1.2 有限元离散

有限元离散过程中，插值函数对计算过程和精度也有较大的影响，传统的节点有限元计算时易出现伪解，处理边界条件也不方便；而棱边元在这些方面具有一定的优势。针对于变压器模型，文献[10]中分析就表明：节点有限元法在计算变压器漏磁时误差较大，而棱边有限元法具有较高的计算精度，更适合变压器的三维场计算。故文中运用Whitney型棱单元的形状函数[11]，采用最常用的四面体离散单元，单元插值函数如下所示。

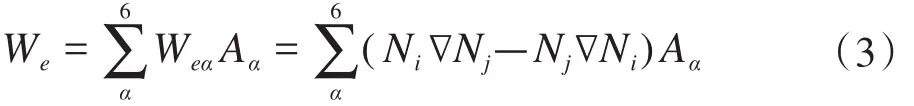
上式中：α为单元棱边的标号；Ni、Nj为单元节点的形状函数；Aα为矢量磁位在棱边上的线积分。

根据式（3），运用加权余量法对式（1）、（2）离散可得如下矩阵方程。

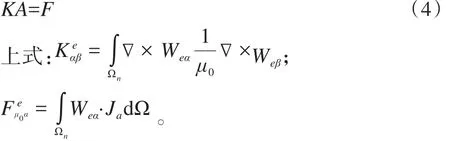
为了文中叙述的方便，此处将变压器整个求解域分为8部分：铁心、油箱组成的无电流区（1部分），原副边三相绕组、故障绕组组成的源电流区（共7部分），则式（4）可写为如下形式。

上式中：Fj、Bj分别为各区域形成的矩阵对整体矩阵的贡献（j=0对应无电流区，j=1~7对应各绕组组成的源电流区）；其中分别为线圈的匝数、总截面积（除去绕组外表皮绝缘部分）和切向方向的单位矢量；Ij（j=1~7）为各绕组电流的大小。

1.3 电路方程

对电路中各支路列出方程可得：

上式中：U、I、E、L、R分别为各支路中的电压源、电流、绕组反电势、电感以及电阻矩阵；其中绕组的反电势e可由下式计算[12]。

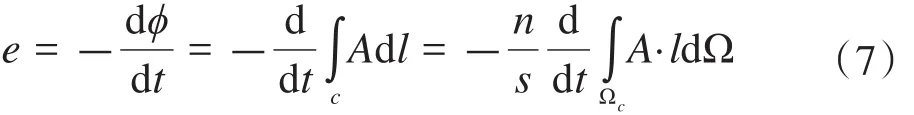
上式中：Ωc为绕组截流区，则式（6）可写成如下形式。

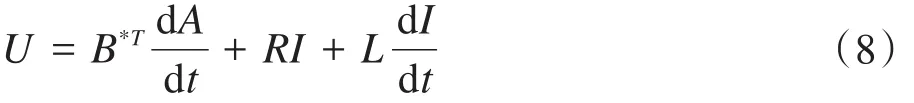
上式中，B*T=[B1B2B3B4B5B6B7]T。

由所得的式（4）场域离散方程和式（8）所示的电路方程可得场-路耦合计算方程如下所示。

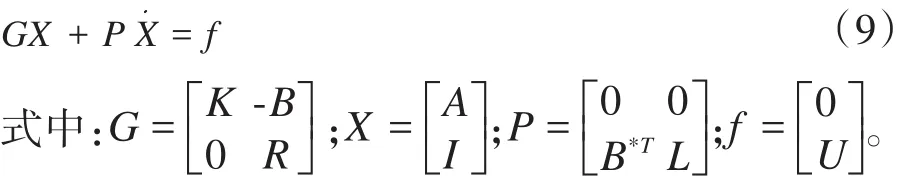
1.4 时间离散

采用Crank-Nicholson离散格式[13]，式（9）对应的离散格式为：

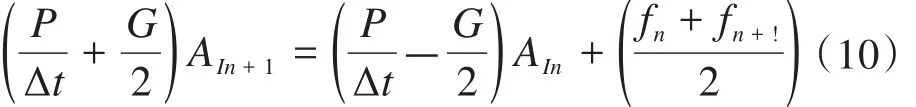
由于求解区域中存在非线性的铁磁材料，式（10）为非线性的矩阵方程，文中采用牛顿-拉夫逊法进行迭代求解，运用ICCG法进行矩阵求解运算即可实现场-路耦合计算。

1.5 铁心损耗计算

文中分析过程中，虽然忽略了铁心涡流效应，但铁心的损耗依然可通过最常用的损耗分离模型进行估算。损耗分离模型认为铁心的损耗可分为三部分表示，如下所示。

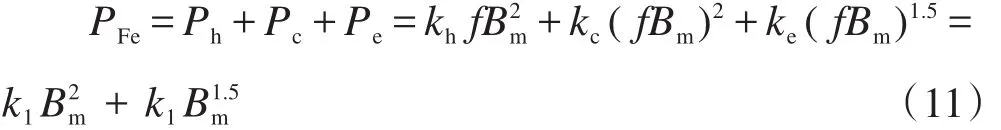
式中：k1=khf+kcf2；k2=kef1.5；kh为硅钢片材料的磁滞系数；kc=π2σd2/（6ρ）为涡流损耗系数，σ为硅钢片的电导率（S/m）；d为硅钢片的厚度（m）；ρ为铁心的质量密度（kg/m3）；ke为附加损耗系数。根据硅钢片厂家提供的损耗曲线，采用最小二乘法可以求出系数k1、k2，进而求出kh、ke，如下所示。

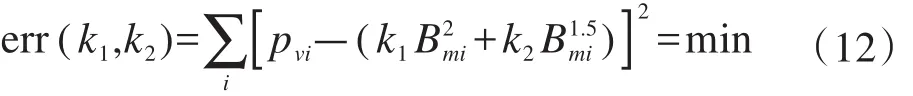
2 仿真模型

文中以S9-500/10型三相电力变压器进行计算，变压器的参数见表1.

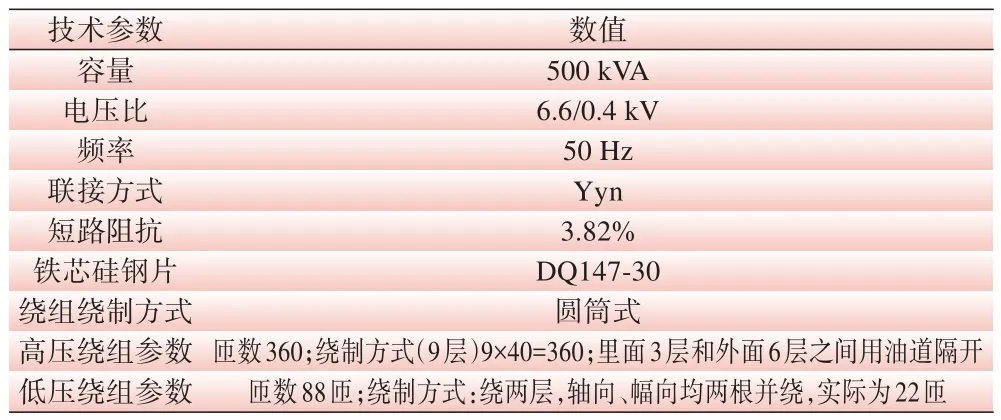
表1 变压器模型参数

建立变压器有限元模型和场-路耦合模型如下图1、图2所示。

图1 变压器有限元模型

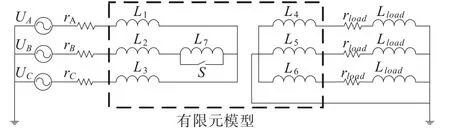
图2 场-路耦合仿真示意图

图2 中：UM、rM（M=A，B，C）为变压器电压激励和内阻；LN（N=1~6）分别对应三相原副边绕组，L7为短路故障绕组，它们分别与式（5）中的Fj、Bj一一对应；rload、Lload为三相对称阻感负载；图中开关S的开断与闭合可以模拟变压器正常工作和内部故障两种状态，变压器内部短路可以被看做是变压器绕组连接方式的改变，从上文可以看出，式（8）只建立了各绕组的独立支路方程，并未考虑绕组的连接方式，因此在式（8）左乘考虑绕组连接方式的变换矩阵即可模拟开关S的开断与闭合（变压器正常工作与内部故障），变换矩阵如下所示。

S断开（变压器正常工作）：

S闭合（变压器内部故障）：

3 基于冻结磁导率的变压器自感互感矩阵

计算瞬时自感互感矩阵的必要性，三相完全对称，三相漏感也不完全一样，变压器工作时，漏感并不是一个定值，漏感参数对新型的变压器保护很重要。

3.1 能量法自感互感矩阵计算的原理

对于空间中两线圈i、j分别通入电流Ii、Ij，则空间中储存的能量为：

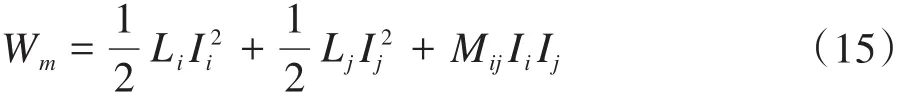
式中：Li、Lj分别为线圈i、j的自感、Mij为其互感。

若对线圈i、j分别通入电流Ii、0 时，空间磁场分布为Bi、Hi，对线圈通入电流为 0、Ij，空间磁场分布为Bj、Hi；当空间中全为线性材料，根据式（15），线圈i、j分别通入电流Ii、Ij时，由叠加定理可知此时空间磁场储能为：

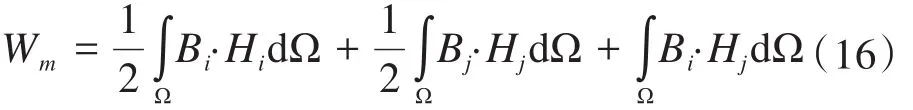
由式（15）、（16）可得线圈的自感、互感分别为：

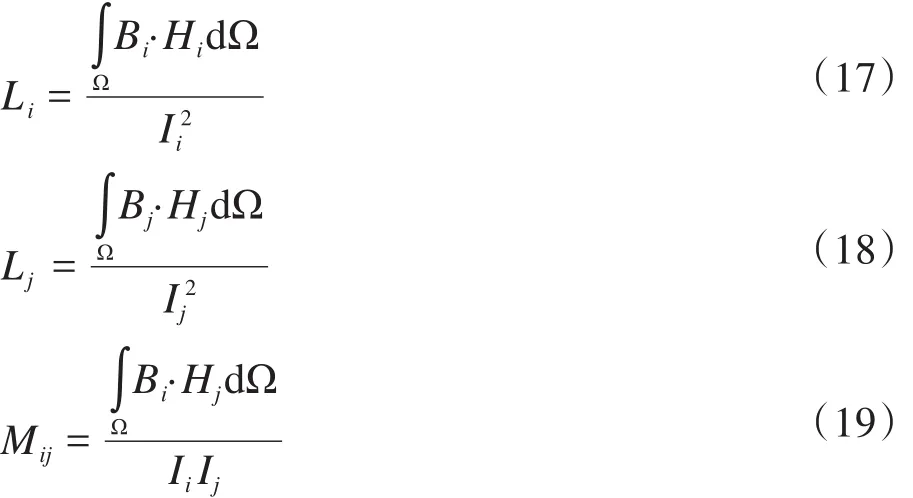
上述计算电感矩阵的前提是模型材料为线性（磁导率为常数），但对于常常分析的电机等设备，多含有非线性的铁磁材料，计算自感互感矩阵时应考虑铁磁材料饱和的影响，计算出来的结果才有实际意义，运用冻结磁导率的方法可解决该问题，具体实现步骤如下：

1）施加激励，根据模型参数，计算模型中非线性材料的工作点，并计算此时每个网格单元的磁导率，冻结各网格单元的磁导率，此时磁导率为常数。

2）根据1）中计算的结果，将非线性材料的磁化曲线替换为1）中保存的磁导率，此时模型材料参数均为线性，对每个绕组施加1 A的激励，运用式（17）~（19）计算模型的自感与互感。

可见，运用冻结磁导率的方法是计算非线性材料工作在不同工作点处的自感、互感，具实际应用价值。

3.2 自感互感矩阵与漏感之间的关系

变压器（有m个绕组组成）的自感互感矩阵表示如下：

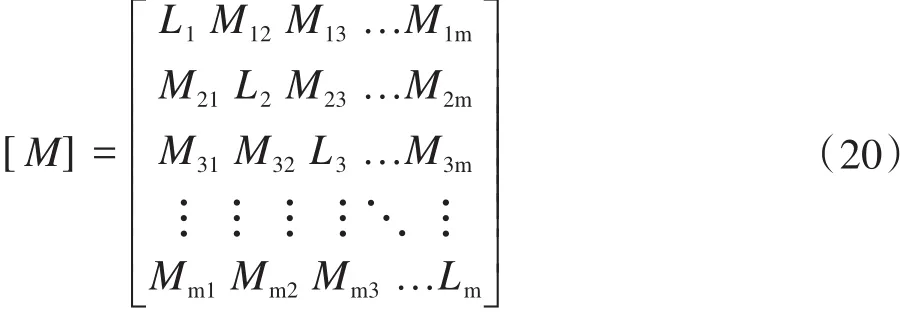
上式中，[M]为变压器的自感互感矩阵。

设绕组m上的电压电流分别为um、im，其关系可由下式表示：

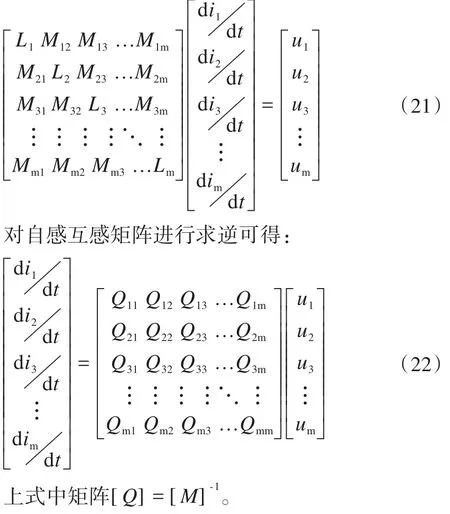
利用短路测试法，仅对一套绕组供电，其余绕组都短路（即绕组端电压为0），此时上式可写为：

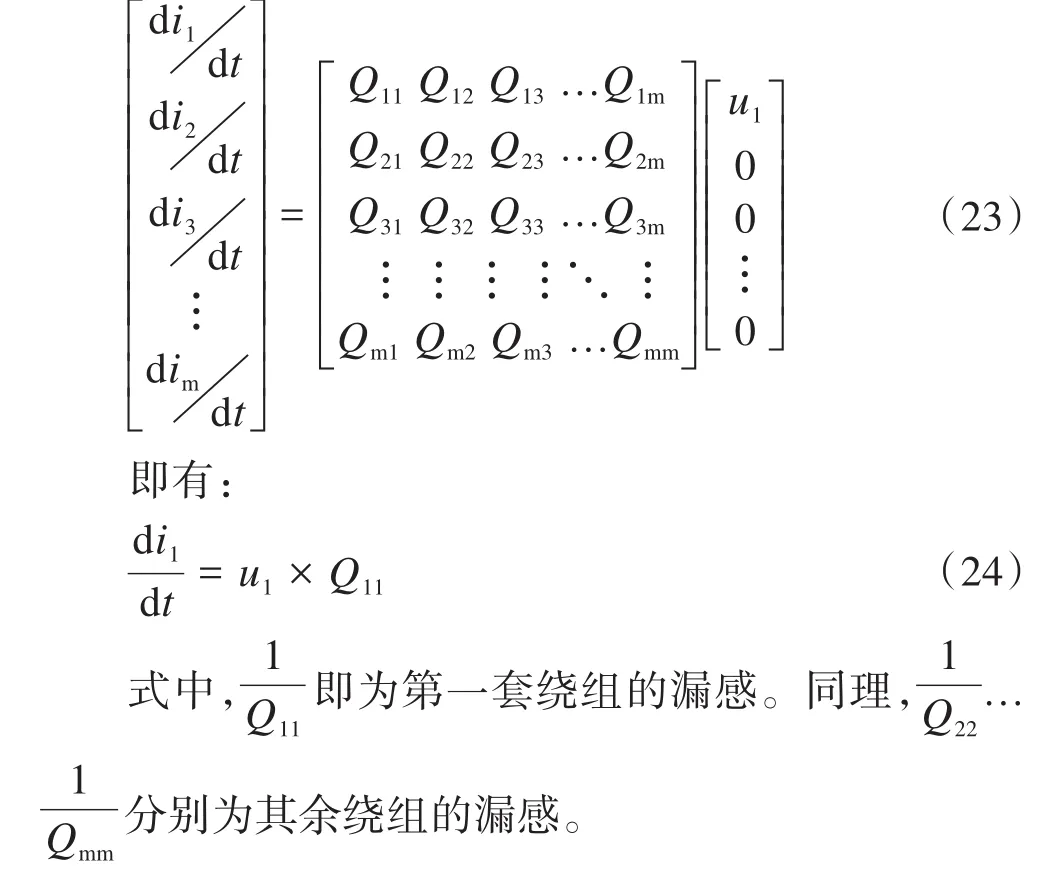
以某一变压器计算为例，计算可得变压器正常工作情况下的漏感变化，如图3、图4所示。

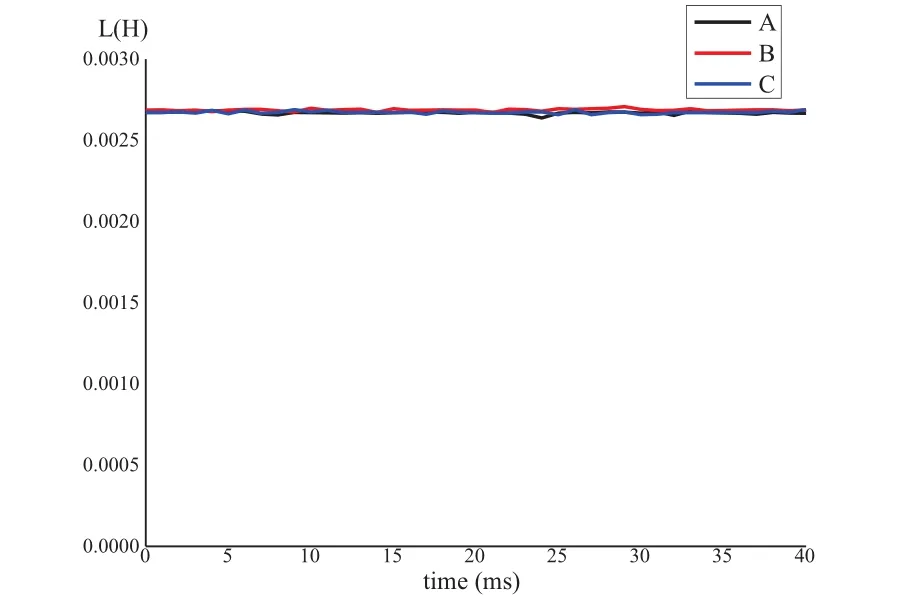
图3 变压器正常工况时原边漏感

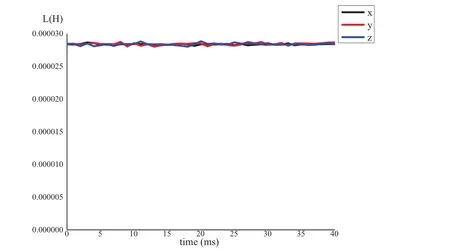
图4 变压器正常工况时副边漏感

变压器空载合闸时候的漏感如图5、图6所示。

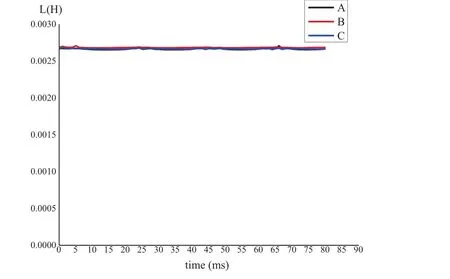
图5 变压器空载合闸时原边漏感

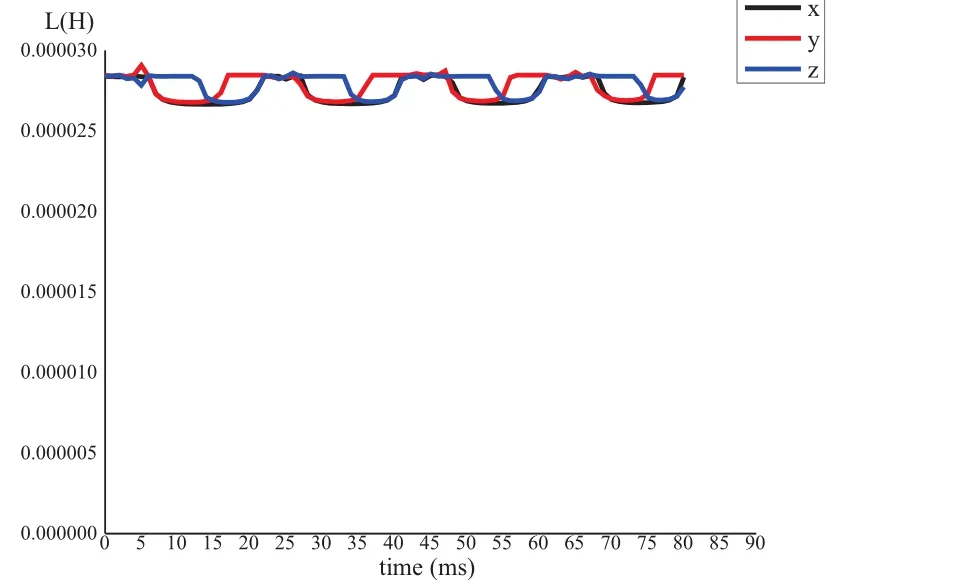
图6 变压器空载合闸时副边漏感

4 结语

1）建立了变压器的场-路耦合模型，对变压器内部故障进行了仿真分析，模型能充分反映变压器内部故障后的特征，分析表明变压器内部故障同时受故障绕组位置和匝数的影响，仿真结果可作为分析变压器内部故障的理论依据。

2）所建立的变压器场-路耦合模型，具有普适性，能够用于分析变压器的其他暂态现象，对分析其他电磁设备也具有一定的借鉴意义。