基于多尺度影响因子的水土保持措施布局研究

宋晓彦

(湖北安源安全环保科技有限公司，武汉 430000)

0 引 言

水土流失不但发生在第四系发育的山地丘陵坡地地区，在冲击平原、三角洲等复杂地表径流区域和复杂浅层地下水发育区域也有发生。所以，影响水土流失过程的因子，较大程度来自浅层地下水的流体动力过程，其次来自地表径流的水土冲刷作用。而表层第四系的稳定性表达，主要来自第四系的发育深度、地表坡度、地表径流及浅层地下水径流量等因子，地表植被及地表防止水土流失的人工构筑物规模也会影响水土流失过程。

相关研究中，采用加权因子累加法构建ArcGIS水土保持模型，对可能发生的水土流失动力过程提供水土保持能力的因子加权，最终对ArcGIS模型进行数据加权，以对区域水土保持能力进行加权赋值。

1 水土保持多尺度因子的构建

1.1 第四系厚度及地表坡度的水土保持因子构建

前期地质调查文献中显示，当第四系厚度较小时，第四系发育不稳定；而当第四系厚度较大且存在一定的坡度时，地质滑坡的可能性增加，水土保持难度也会随之增大，所以第四系厚度与地表坡度应联合分析。即地表坡度与水土保持难度的关系为逆幂函数，而第四系厚度与水土保持难度的关系为二次函数。两函数相乘，可得：

(1)

式中：α、β分别为第四系厚度系数与地表坡度系数；M为X象限位移值；N为Y象限位移值；B为地面坡度系数的修正量；e为自然常数。

为确定式(1)中α、β值，可以约定一个规律常数表，见表1及表2。

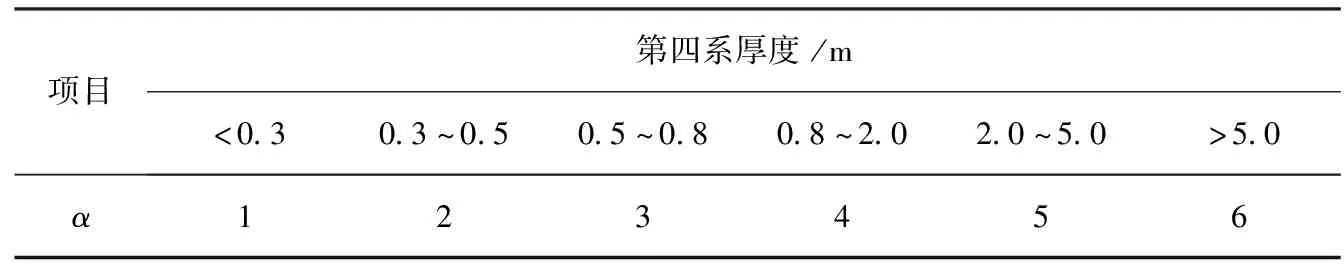
表1 第四系厚度因子对应表

表2 地面坡度因子对应表

由表1与表2可知，因为在式(1)中已经对相应的α、β值分布规律依照逆幂率规律和抛物线规律做出了数学表达，所以α、β值在两表中的赋值属于线性赋值，无需进行基于相应数学关系的非线性赋值过程。对两组因子进行线性赋值，目的是增加后期数学函数设计的自由度，确保式(1)中待回归因子B、M、N等的实际数学意义更加简化。

1.2 地表植被及水土保持构筑物的水土保持因子构建

地表植被与水土保持构筑物对区域水土保持能力的促进作用可以看作近似线性关系。其中，乔木覆盖率与灌木覆盖率对水土保持的支持力度较强，而草本覆盖率对水土保持的支持力度较弱。地表水土保持构筑物包括拦水沟、引水渠、挡土墙等的完善程度，对区域水土保持能力的影响也有线性关系。多种影响之间可采用加权累加的方式进行数据控制：

N2=0.60·(0.50·λH+0.35·λM+0.15·λL)+0.40·γ

(2)

式中：λH、λM、λL分别为乔木、灌木、草本植物的覆盖率传导因子；γ为地表构筑物的传导因子。

为确定式(2)中λH、λM、λL、γ的取值，可以约定一个规律常数表，见表3及表4。

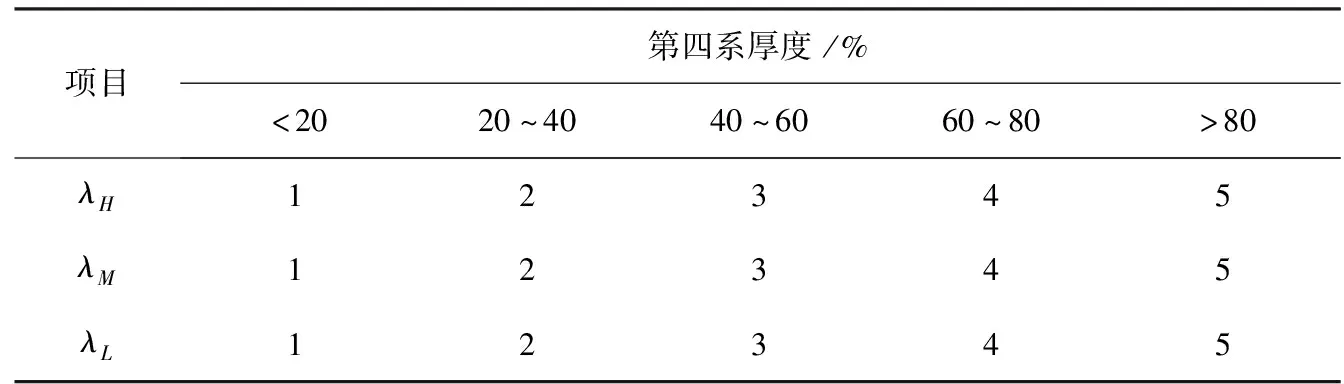
表3 地面植被因子对应表

表4 地面构筑物因子对应表

表3中需要传导的数据，已经在式(2)中给出加权参数，所以3个因子λH、λM、λL在表3中依照线性关系进行赋值，无需考虑三者对最终因子的实际加权特征。此方案可以对式(2)中的实际加权因子意义进行自由度更高的管理控制。

表4中对γ的赋值同样采用线性关系进行赋值。其中，“没有”选项指在分析区域内以及分析区域外扩100 m范围内，没有任何相关的地面构筑物进行水土保持辅助控制；“初级”构筑物表示区域内拥有人造水渠等设施进行初步控制；“一般”表示区域内已经构筑相对完善的地表构筑物进行水土保持辅助控制，但其功能并不能完全或有效的发挥；“完善”表示区域内拥有功能健全且维护合理的水土保持地面构筑物体系。

1.3 地表径流及地下水渗流的水土保持因子构建

地表径流量来自移动式或便携式水文站提供的区域内地表径流量数据，根据相关文献研究资料，地表径流量越大，水土保持的难度越大。地下径流量以钻孔抽水数据为准，所以其控制函数可以写作：

(3)

式中：ζD、ζU分别为地下径流量和地表径流量数据。因为这两个数据为逆函数关系，所以需要取倒数后进行函数分布，使用对数函数进行近数轴0点的数据关系放大投影。

这两个数值的实际传导因子设计情况，详见表5与表6。

表5 地面径流因子对应表

表6 地下径流因子对应表

表5与表6中，ζD、ζU在径流量较小的情况下赋值较小，而径流量较大的情况下赋值较大，其统计学本质是水土流失的数据描述而非数据保持的数据描述。所以在式(3)中，使用倒数函数对其进行调用，此设置模式也是为了增加加权因子的统计学意义。

1.4 水土保持因子的整体构建

式(1)-式(3)中，N1、N2、N3分别代表地质地层对水土保持能力的影响因子、地表植被及地表附着物对水土保持能力的影响因子、水体环境对水土保持能力的影响因子。这3个因子可以进行加权累加进行水土保持因子N的构建：

N=0.55·N1+0.20·N2+0.25·N3

(4)

式中：对N1、N2、N3的加权因子分别为0.55、0.20和0.25，该因子的确定过程来自对3个因子的作用机制进行预估，且在后续的仿真数据吻合研究中，这3个因子的数据表现可以支持本文研究的实际需求。

2 地质区域个案及数据仿真分析

2.1 地质调查区域的个案特征

某区域位于鄂东低山丘陵地区，区域面积为15 km×15 km。区域内山体坡度最大为16°，其中山体坡度5°～12°区域占丘陵区域总面积70%以上。区域内两条山溪向下汇入某区域小流域河流，山溪流量分别为120～330和180～390 m3/h。第四系方面，该区域山区第四系厚度0～2.5 m，平均0.63±0.15 m；坡积平原区域第四系厚度1～12 m，平均5.82±0.54m;淤积平原区域第四系厚度5～32 m，平均12.75±3.22 m。山溪部分中上游一般切削第四系至基岩，山溪两岸第四系厚度0～1.8 m，山溪最大水深1.2 m，为季节性山溪。小流域河流水深1.2～3.5 m，底部第四系发育，厚度1.2～18.5 m。

在ArcGIS中对区域进行划分，每单元为25 m×25 m，即将区域划分为600×600个方格，共36万个，对每个方格进行N1、N2、N3和N值的赋值，通过对小流域河流载沙量对水土流失情况进行检测，以判断上述模型带来的水土流失情况并判断其水土保持能力。

2.2 多尺度水土保持因子的实证分析

对N1、N2、N3和N值的加权情况，依据均值法进行计算，即计算N1、N2、N3的每项均值，同时计算N值的每项均值。对河流载沙量的计算为每月采集1次，采集过程考察区域内地质条件对N1、N2、N3和N值进行补充调查并重新计算，所得结果见表7。

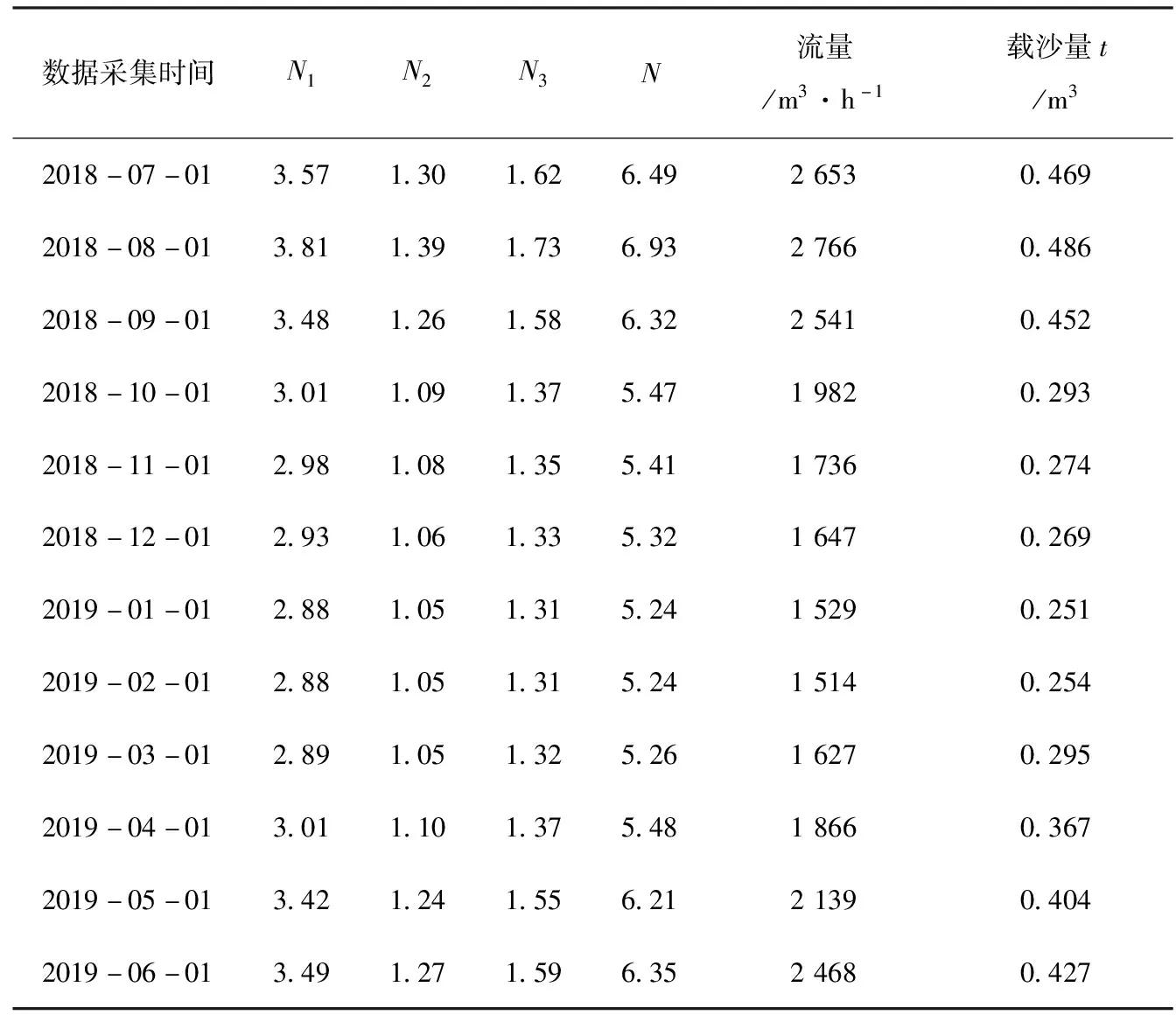
表7 基于个案的实证数据对照表

由表7可以看到，该个案河流的流量与载沙量变化幅度较大，但N值变化幅度较低。其中，N值最大值6.93，最小值5.24，变化幅度为32.3%；而总载沙量在8月份达到峰值1 344.3 m3/h，在2月份达到谷值384.8 m3/h，变化幅度为249.4%。但N值与总载沙量的峰谷值出现较为统一，周期内数据接近线性关系。所以，将表7中数据进行可视化，见图1。

图1中，N值与总载沙量数据符合回归公式Y=579.08X-2 607.1，R2值为0.956 7；N值与单位载沙量数据符合回归公式Y=143.23X-478.76，R2值为0.916 3；两组数据的线性关系的R2值均超过0.900，证实其线性关系显著。同时证明本文设置的多尺度水土保持影响因子与实际测量值的吻合度较高，该加权模式具有显著的统计学意义。

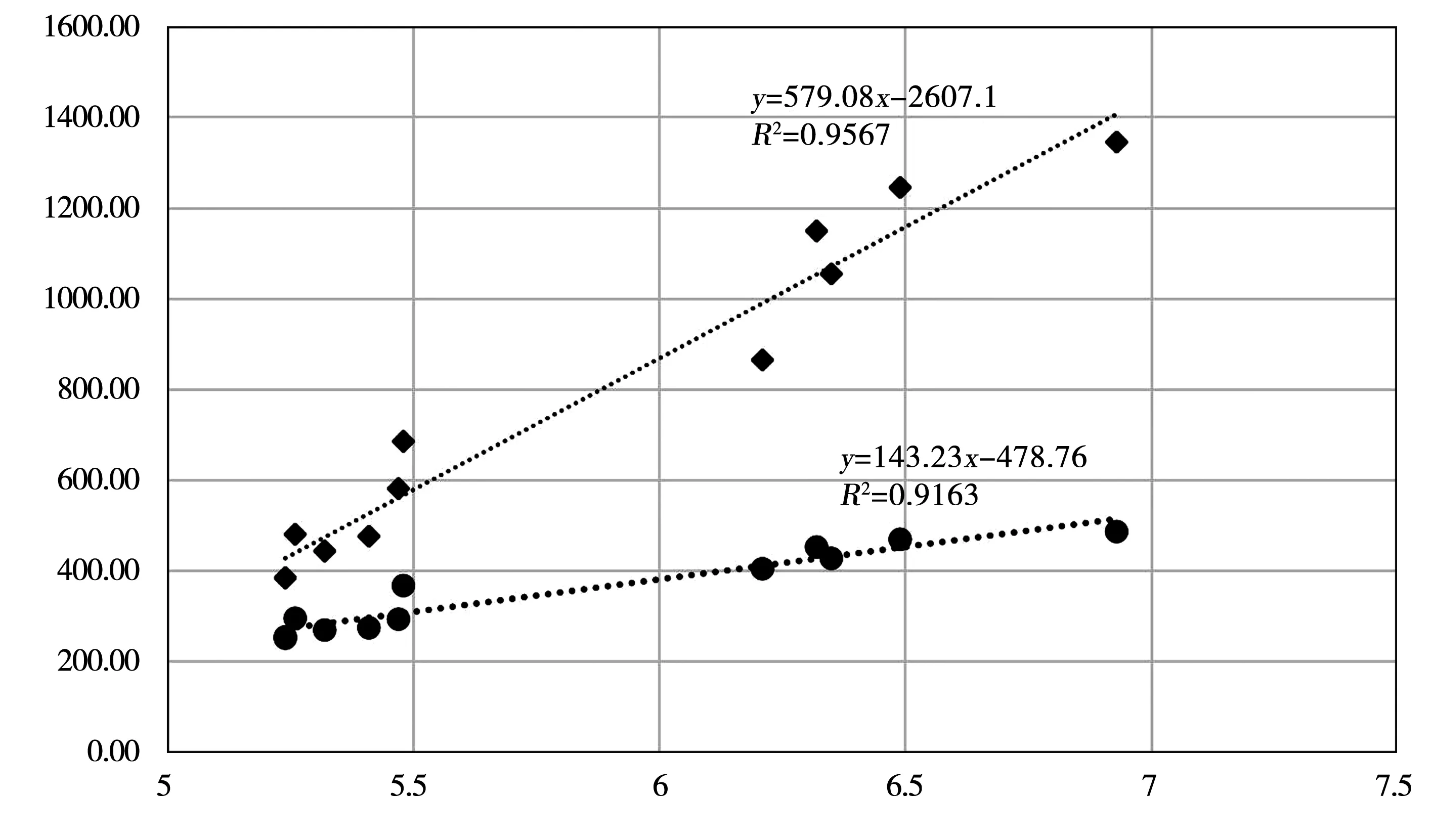
图1 河流载沙量数据与N值统计学关系图

3 结 语

从地质学和环境学角度进行分析，区域水土保持能力与地形地貌和第四系发育情况有关、与地表植被及用于水土保持的地表构筑物有关、与区域地表径流和地下径流的流量有关。本文在此基础上，构建了水土保持能力因子并进行了加权累加。在实证分析过程中，通过对区域内河流单位水体载沙量和总流量载沙量数据进行水土流失的限定发现，本文设定的因子与实际测量数据之间存在统计学相关性。研究结果证明，本文设置的多尺度水土保持影响因子与实际测量值的吻合度较高，该加权模式具有显著的统计学意义。