浅埋大采高工作面超前支承压力峰值演化规律
2021-03-02黄庆享贺雁鹏
黄庆享,李 锋,贺雁鹏,高 彬,李 军
(1.西安科技大学 能源学院,陕西 西安 710054;2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室,陕西 西安 710054;3.陕煤集团神木张家峁矿业有限公司,陕西 榆林 719000)
0 引 言
中国西部榆神府矿区主采煤层为2-2、5-2两层厚煤层,2-2煤层平均厚度6.5 m,该煤层埋藏浅、基岩薄、覆盖厚松散层,适合大采高一次采全高[1-3]。浅埋大采高开采,顶板破断直接波及地表,来压期间有明显的顶板台阶下沉和动载现象[4-7]。工作面超前支承压力是顶板破断运动后煤壁前方原岩应力重新分布的结果[7]。研究浅埋大采高工作面超前支承压力规律,是揭示顶板超前破断规律和结构形成过程、确定超前支护范围和回撤通道保护煤柱尺寸以及开展来压监测预报的基础,对安全高效开采具有重要意义。
国内外对常规埋深工作面超前支承压力规律开展了大量研究[8-10],得出超前支承压力分布规律和开采深度关系不大[11-13],主要取决与采高和顶板岩性;采高越大,峰值距离煤壁越远(平均为1.27倍采高),峰值系数基本不变[14-15]。关于浅埋煤层超前支承压力研究,任艳芳等认为浅埋工作面超前支承压力分布规律与常规埋深类似[16];黄庆享等发现陕北浅埋大采高工作面超前支承压力峰值随采高的增大降低,峰值位置与煤壁距离约为采高的2倍[17];秦忠诚等研究得出东胜转龙湾煤矿浅埋工作面末采阶段超前支承压力影响范围约为20 m,据此优化了回撤通道间保护煤柱尺寸[18];王创业等预测了浅埋大采高工作面支承压力峰值点位置[19]。可见,超前支承压力是岩层控制关注的热点,而关于浅埋大采高工作面超前支承压力规律的研究较少。
以神南矿区张家峁煤矿22201浅埋薄基岩大采高工作面为对象,在采场顶板破断规律和来压规律实测基础上,利用UDEC数值计算和物理模拟,分析3~7 m采高时的工作面超前支承压力峰值演化特征与规律,给出了超前支承压力峰值位置的计算公式,得到了现场实测结果的验证。本文研究为确定顶板超前破断位置与支承压力峰值的关系,揭示顶板结构运动与压力转移的关系,提供了重要依据;还可为工作面巷道超前支护范围确定、末采回撤通道煤柱初次优化、超前来压监测预报等提供重要的科学依据。
1 工程背景
张家峁煤矿22201工作面为2-2煤层首采工作面,地表地形地貌属风沙滩地区,煤层赋存稳定,倾角1°~2°,煤层厚度7.3~9.6 m,采高6 m,平均埋深约95 m。顶板中完整基岩厚度约16~20 m,风化基岩厚度约16~20 m,松散层厚度约40~50 m,工作面属于典型的浅埋薄基岩大采高工作面[1]。工作面综合柱状图如图1所示。
2 变采高超前支承压力演化机理
2.1 计算模型
以张家峁煤矿浅埋薄基岩大采高22201工作面为背景,建立UDEC数值计算模型(图2)。模型长×高=300 m×95 m,模拟采高3~7 m。模型顶部为自由边界,底部边界限制垂直位移,两侧水平方向施加位移约束。模型材料本构关系选取摩尔—库伦,节理本构关系选取面接触的库伦滑移,煤岩力学参数见表1。
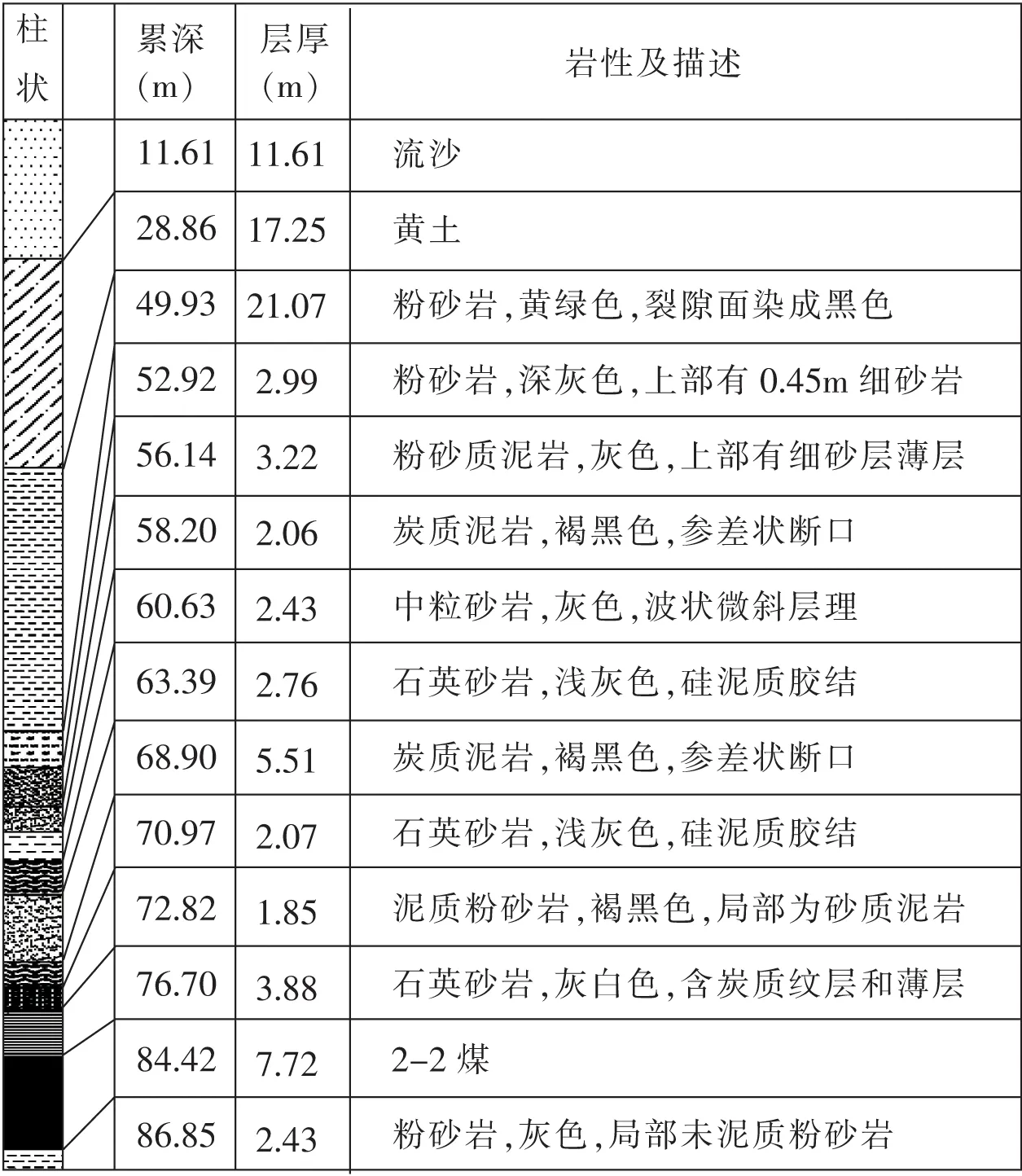
图1 工作面综合柱状图Fig.1 Comprehensive cylindrical map of working face
图2 数值计算模型Fig.2 Numerical simulation model
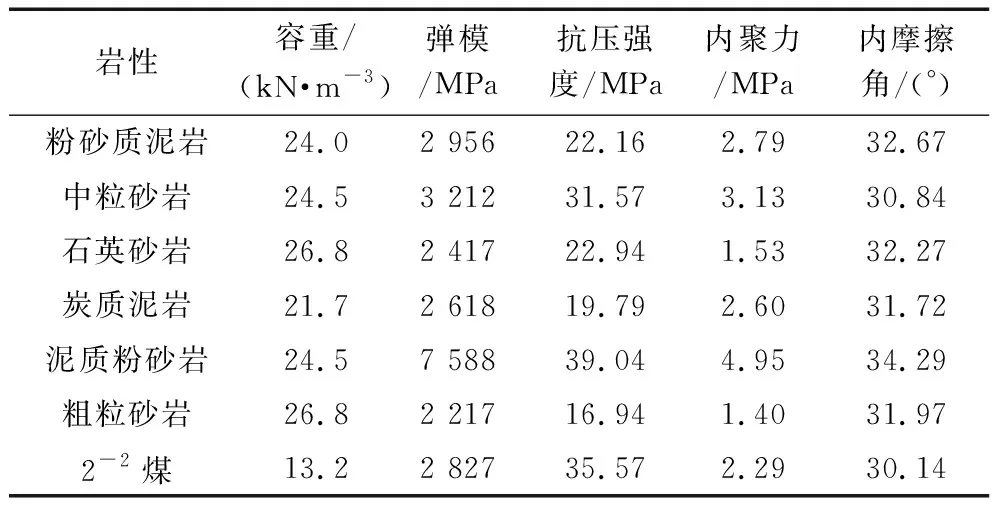
表1 煤岩体力学参数
模型左右边界各留50 m边界煤柱消除边界效应,模拟工作面沿走向开采200 m。开挖过程中,在煤层底板布设应力测线,计算出工作面开挖过程中超前支承压力,分析浅埋大采高工作面超前支承压力峰值演化规律。
2.2 超前支承压力演化特征
在开采条件一定的情况下,计算3,4,5,6和7 m采高的工作面超前支承压力。
初采阶段工作面超前支承压力分布如图3所示。随着采高的增大支承压力峰值减小不大,峰值点距煤壁距离增加,影响范围约20 m。
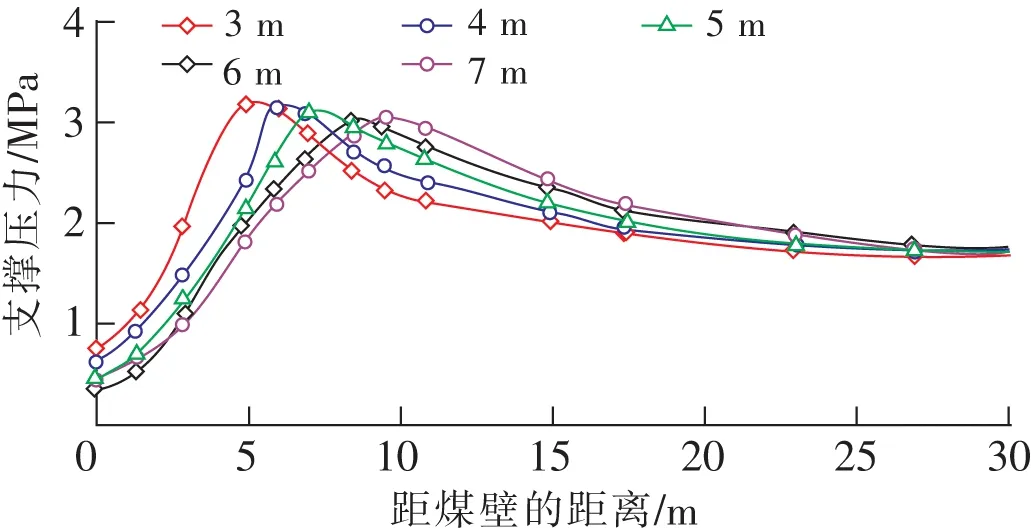
图3 初采阶段不同采高超前支承压力分布演化规律Fig.3 Front abutment pressure of different mining heights at initial mining stage
充分采动后不同采高工作面超前支承压力分布曲线如图4所示,充分采动后工作面超前支承压力峰值随着采高的增大而减小,压力峰值向煤壁深处转移,支承压力影响范围约25 m,比初采阶段影响范围增大25%。
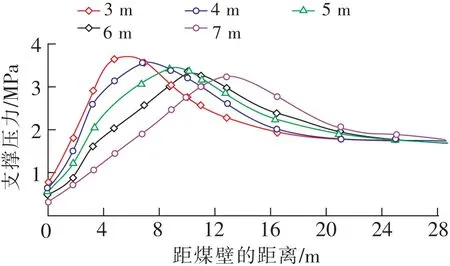
图4 充分采动后不同采高超前支承压力分布演化规律Fig.4 Front abutment pressure of different mining heights after critical mining
充分采动后,随着采高的增大,支承压力峰值数值和位置都大于初采阶段。
初采和充分采阶段的工作面超前支承压力峰值和峰值位置随采高的演化规律如图5所示。初采阶段,随采高3 m增大到7 m,峰值系数(峰值与原岩应力比)由1.92下降为1.83,下降5%。峰值位置距煤壁距离从4.9 m增大为9.4 m,绝对值增加了92%;与采高比从1.63倍降为1.34倍,与采高比降低18%。
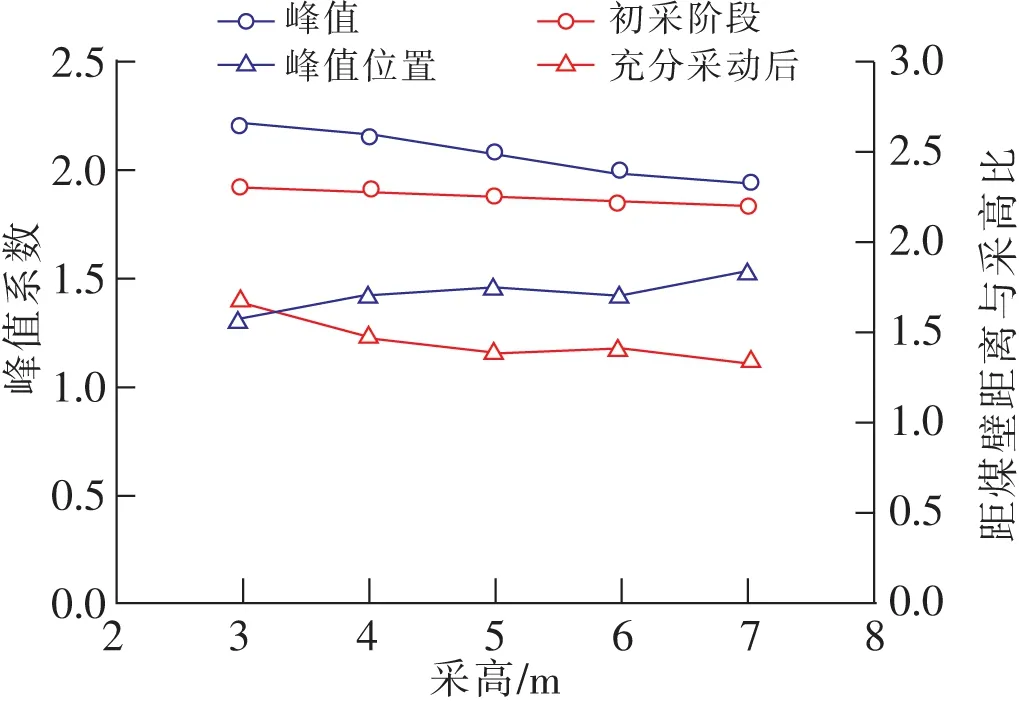
图5 压力峰值和位置与采高的关系Fig.5 Pressure peak and position vs mining heights
充分采动后,随着采高由3 m增大到7 m,支承压力峰值从原岩应力的2.20倍下降为1.94倍,减小14%;峰值位置从4.8 m增大为12.8 m,绝对值增加了167%;与采高比从1.60倍上升为1.83倍,与采高比增加了14%。
初采阶段和充分采动阶段,压力峰值与采高成近似线性关系。峰值位置却出现分化,初采阶段峰值距离煤壁与采高的倍数呈非线性降低趋势,充分采动后呈非线性增加趋势。支承压力峰值大小及距煤壁的距离与采高关系如下
初采阶段
(1)
充分采动后
(2)
式中m为采高,m;σymax为支承压力峰值,MPa;σz为原岩应力,MPa;x0为峰值距煤壁距离,m。
3 6 m大采高超前支承压力分布规律
以张家峁煤矿22201工作面条件,按照几何相似比αl=100制作物理相似模型,模型长×宽×高=3 m×0.2 m×0.95 m,容重相似比αγ=1.5,应力相似比ασ=50,模拟采高6 m。在模型底板上布置CL-YB-114WX1无线测力传感器监测工作面开采过程煤壁超前支承压力。
模拟工作面推进到33 m,顶板初次垮落,高度15 m,工作面初次来压,老顶形成“非对称三角拱”结构,如图6所示。工作面初次来压时,超前支承压力分布如图7所示,物理模拟压力峰值2.98 MPa,超前煤壁8.5 m,为采高的1.42倍。数值计算压力峰值3.05 MPa,超前煤壁8.5 m,为采高的1.42倍。两者基本一致,后面采用数值模拟结果表述。
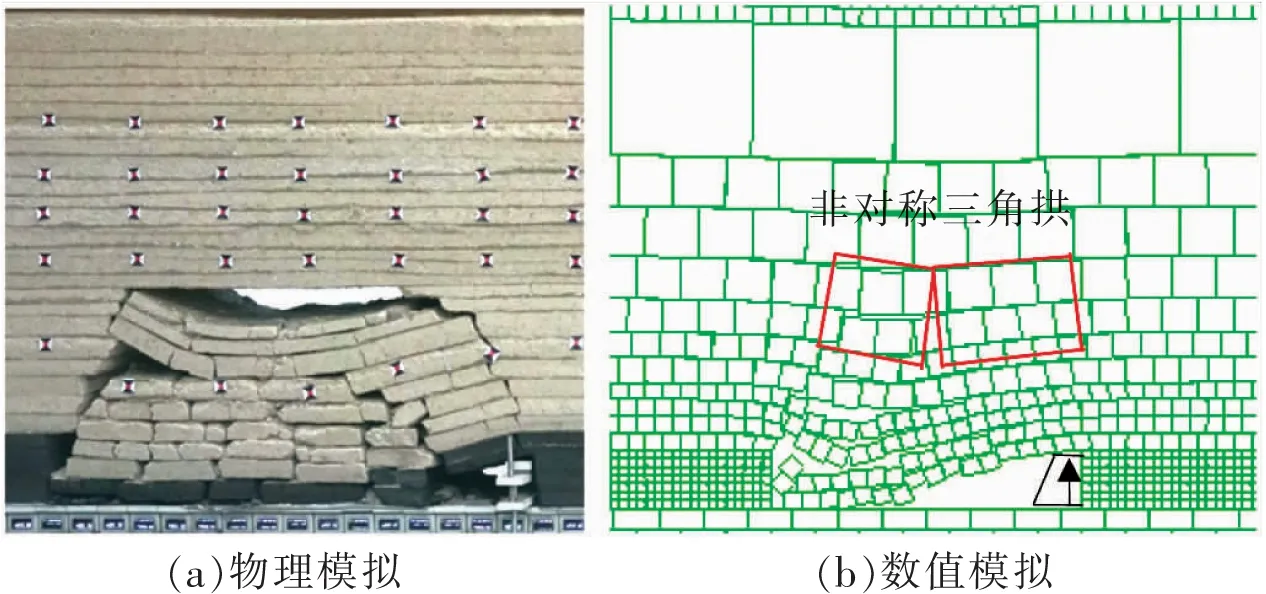
图6 初次来压覆岩垮落形态Fig.6 Overburden collapse forms of first weighting
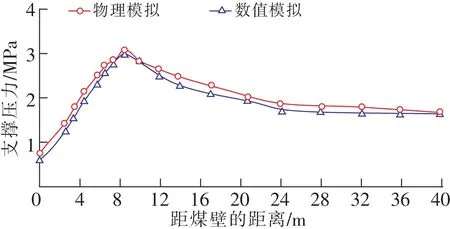
图7 初次来压超前支承压力分布Fig.7 Front abutment pressure distribution of first weighting
工作面第1次周期来压覆岩垮落形态如图8所示。来压步距12 m,煤层顶板上方20~35 m层位的老顶关键层破断,覆岩裂隙带发育高度35 m,岩层破断角约64°。

图8 周期来压覆岩垮落形态Fig.8 Overburden collapse forms of periodic weighting
第1次周期来压时工作面超前支承压力分布曲线如图9所示。来压时,支承压力峰值3.1 MPa,峰值超前工作面煤壁前方9 m,为采高的1.50倍,支承压力影响范围25 m。
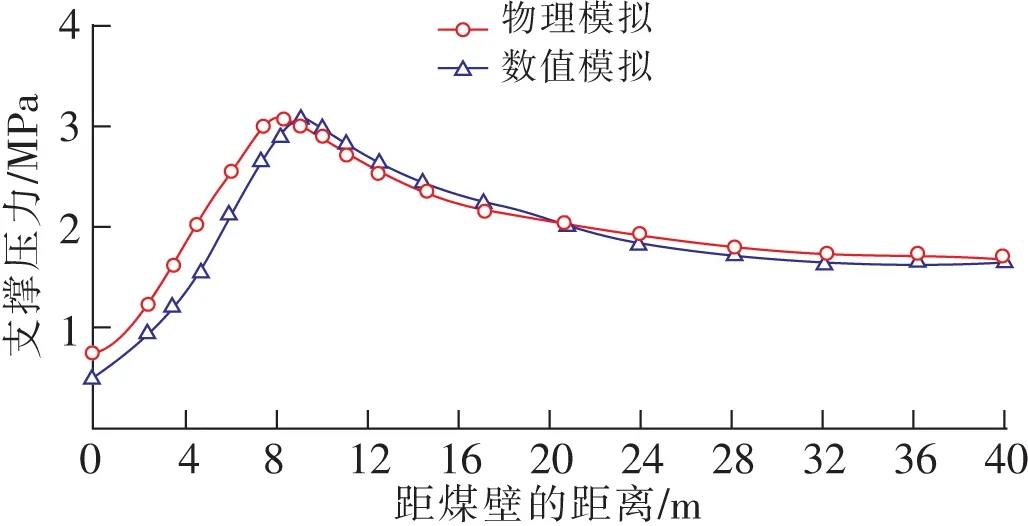
图9 第1次周期来压超前支承压力分布Fig.9 Front abutment pressure distribution of the first periodic weighting
工作面推进到75 m时,工作面达到充分采动,覆岩垮落形态如图10所示。顶板在煤壁前方约7 m位置出现超前破断,形成台阶岩梁结构。
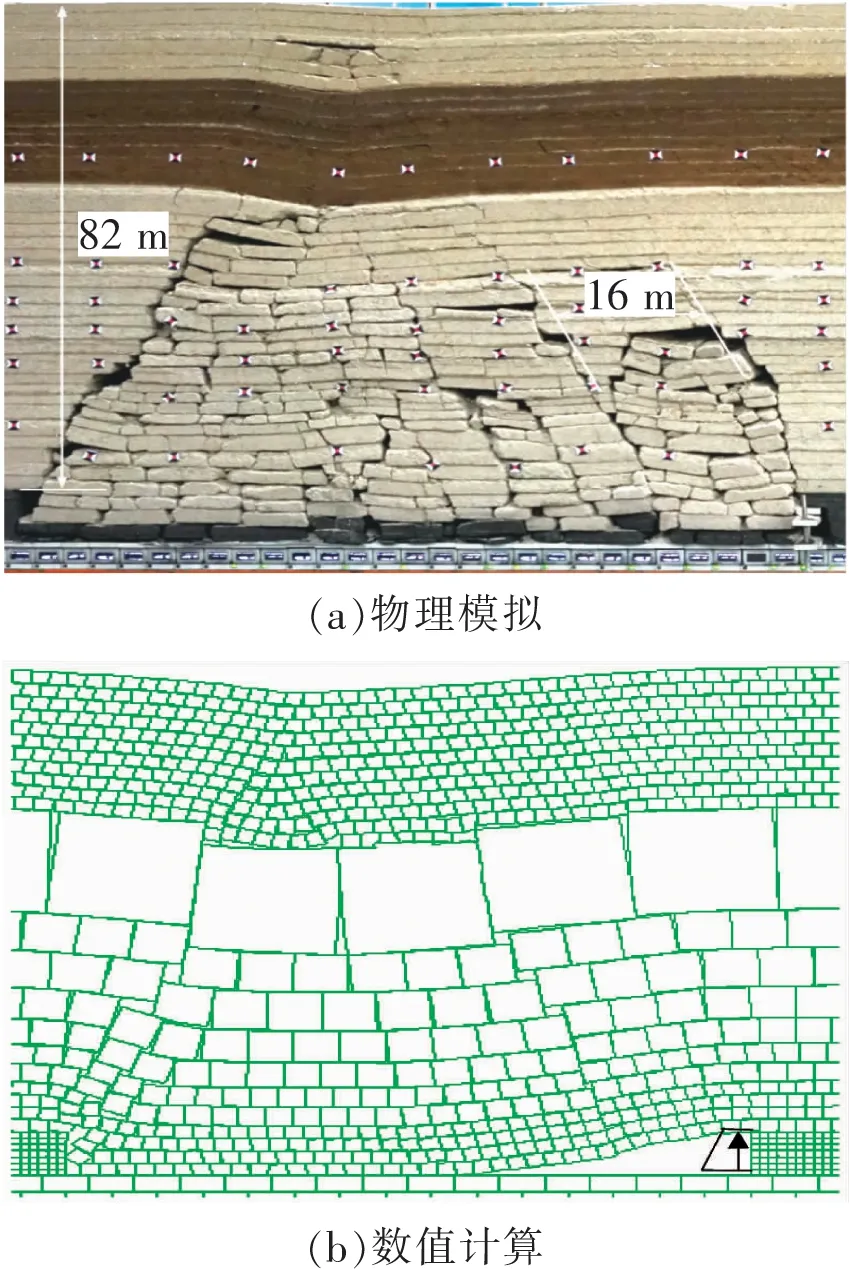
图10 充分采动覆岩垮落形态Fig.10 Overburden collapse forms of critical mining
充分采动后的周期来压期间,超前支承压力规律变化不大,如图11所示。压力峰值3.1 MPa,峰值距煤壁平均9.4 m,为采高的1.57倍。
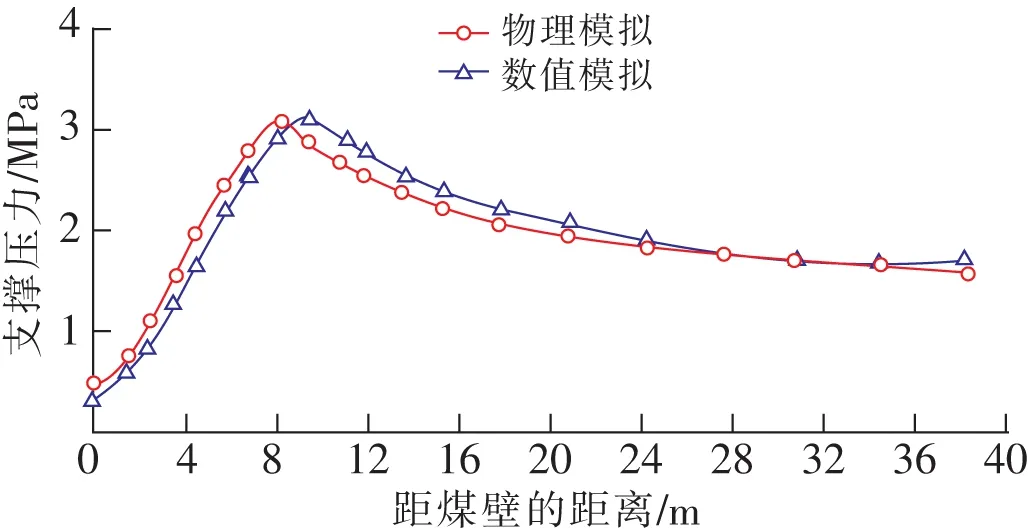
图11 充分采动后超前支承压力分布Fig.11 Front abutment pressure distribution of after critical mining
据物理模拟和数值计算,张家峁煤矿22201工作面在6.0 m采高条件下,工作面超前支承压力峰值为原岩应力的1.84倍(初采)~1.87倍(充分采动),峰值位置距工作面煤壁的距离为采高的1.42倍(初采)~1.57倍(充分采动)。
4 超前支承压力峰值位置理论分析
4.1 超前峰值位置的确定
根据工作面超前煤体受力特征,可分为3个区(图12),松弛区内煤体出现松动,承载能力下降,应力低于原岩应力;塑性承载区的煤体具有一定承载能力,应力高于原岩应力;弹性区包括应力增高区和原岩应力区。
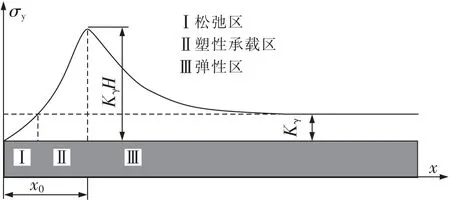
图12 工作面前方煤体受力分区Fig.12 Pressure zones in front of working face
假设煤层是均质连续的各向同性体,在埋深H处,任意取一单元体煤,单元体煤上所受的垂直应力σz为原岩应力[7],即
σz=γH
(3)
式中γ为覆岩体积力,kN/m3;H为埋深,m。
22201工作面埋深95 m,原岩应力1.65 MPa。
煤体的承载能力随着远离煤壁边缘而增大,在距离煤壁边缘一定距离内,存在煤体承载能力与支承压力的极限平衡状态,采用煤岩体极限平衡理论,得出极限平衡区内的支承压力σy[20-21]
(4)
令工作面超前支承压力峰值σymax=KγH,K为峰值(应力集中)系数,压力峰值距工作面煤壁水平距离x0为[21]
(5)
式中m为采高,m;f为煤层与顶板接触面的摩擦因数;α为煤体内摩擦角,(°);τcotα为煤体自撑力,MPa。
据式(5),在内摩擦角α和摩擦因数f为定值情况下,x0随着采高m的增大而增大,峰值位置x0与采高m近似成线性关系。
4.2 现场验证
以22201工作面为例,按照表2计算参数,计算得出工作面超前支承压力峰值距煤壁距离9.5 m,为采高1.6倍,理论计算与数值分析和物理模拟结果吻合。

表2 超前支承压力峰值计算参数
根据张家峁煤矿22201工作面回风顺槽和运输顺槽超前支架压力变化规律,工作面两顺槽超前支承压力峰值距工作面煤壁8~10 m,为采高的1.5~1.7倍,影响范围20 m左右。
实测结果与数值分析、物理模拟、理论计算结果一致,表明上述研究结果可靠。
5 结 论
1)工作面超前支承压力峰值随采高增大而减小,峰值向煤壁深处转移。采高由3 m增大到7 m时,初采阶段支承压力峰值由原岩应力的1.92倍下降为1.83倍,下降了5%;峰值距煤壁距离增大了92%,但与采高之比由1.63下降为1.34,下降了18%。
2)充分采动后,支承压力峰值由原岩应力的2.20倍下降为1.94倍,下降了14%;峰值距煤壁距离由采高的1.60倍上升为1.83倍,上升了14%。充分采动后,随采高的增大,支承压力峰值和峰值距煤壁距离都大于初采阶段。
3)通过工作面煤岩体极限平衡理论分析,给出了支承压力峰值位置计算公式,超前支承压力峰值位置与采高呈近似线性关系,理论计算与实验和实测吻合。
