航空网络关键节点辨识的核极限学习机算法研究

牛军锋，甘旭升，孙静娟，涂从良

(1.西京学院 管理技术系, 西安 710123) (2.空军工程大学 空管领航学院, 西安 710051)

0 引 言

随着国际国内机场、航路航线数量的指数式爆炸增长，以城市机场为节点、航线为连边的航空网络逐渐形成。航空网络的发展水平反映了国家的社会和经济状况，是国家实力的一种象征。在平时，航空网络为社会各产业提供了交流和输出平台，促进了经济发展。在战时，航空网络担负着战斗物资转移与战斗支援任务，直接影响战争进程。

当前，辨识航空网络关键节点的理论研究已成为热点。以往的关键节点辨识方法存在的不足主要体现在两个方面：其一，重视网络拓扑性质及其节点相互关系，没有考量网络边权。例如，H.W.Corley等通过研究删除节点后的最短路径来评估删除节点的重要性；D.Gomezb等比较了接近中心性、介数中心性和度数中心性指标，并引入博弈论评估了网络节点的重要性；He Nan等根据节点度、效率研究了复杂网络节点的重要排序问题；谭跃进等在定义凝聚度基础上提出了一种评估节点重要度的节点收缩方法，将收缩后网络凝聚度最大的节点视为最重要的节点。上述研究主要适用于不带权网络，但基本没有考虑航空网络中航线流量的影响。其二，方法过于单一，一般仅考虑节点的某一性质。例如，谢凤宏等根据复杂网络关键节点辨识算法的缺点，提出了一种基于加权聚类系数的复杂网络节点重要度排序方法；Chen Duanbing等根据每种中心性度量自身缺点，将几种不同的中心性度量多属性化，并采用层次分析法对多属性进行聚合，得到各节点的影响评估值；王建伟等依据网络中节点的局域特征，提出了一种基于近邻节点度节点重要性的度量方法。上述研究简便高效，不足之处是机场节点的重要性影响因素十分复杂，仅考虑个别性质往往难以获得准确结论。

通常采用接近中心度、介数、网络连接密度以及网络效率来综合评估节点的重要性。然而在实际计算中，上述指标通常涉及最短路径等复杂度高的运算，导致评估过程耗时过长，进而影响关键节点的辨识效果。因此，本文以节点度值、点强和

K

-shell值等简单指标作为输入，以由复杂指标得到的综合重要度作为输出，选取少量节点训练改进型极限学习机(Extreme Learning Machine，简称ELM)模型，对航空网络关键节点进行辨识，并以中美两国航空网络为例进行仿真验证。

1 节点简单指标

航空网络对关键机场的研究主要是指标分析，指标较少时评估准确度不够理想，指标较全面时计算的时间复杂度又很高。

简单指标值为训练知识数据库，本文选取节点度值、点强、

K

-shell值作为简单指标。

节点度值：反映网络中单个节点与相邻节点间连接次数的指标，定义为节点的直接连边数。

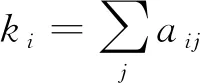
(1)

式中：

a

为两节点间的连边状况。若节点

v

和

v

不存在直接连边，则

a

=0；否则，

a

=1。点强：主要指航空网络中的边权，即航线流量。点强

S

的表达式为

(2)

式中：

w

为与节点

v

直接连边的权值；

N

为节点

v

的相邻节点集合。

周围机场与该机场节点联系越紧密，连边权值就越大。

K

-shell：

K

-shell法是节点排序的代表性算法，根据节点度或其他指标，将处在网络外壳的节点一层一层剥离，剥离越晚的节点就越重要，如图1所示。其具体步骤是：搜索网络中度为1的节点，删除此类节点及其连边；删掉这些节点后，网络结构出现变化，将此时度是1的节点及其连边删除，依此过程，继续删除节点，直至网络中不包含度为1的节点。将删掉的节点组成的壳作为1-壳(即

Ks

=1)。同理，继续去除节点度为2的节点，作为2-壳，以此类推，直至删完所有节点。这种方法对节点进行的是粗粒化排序，虽然精度不高，但反映了节点的全局性质。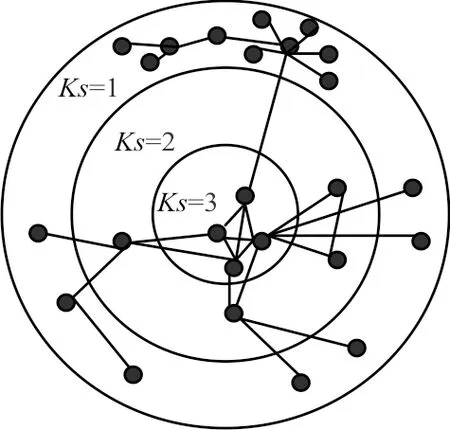

图1 K-shell方法示意

对于节点

v

，其

K

-shell值为

Ks

，该值越大，节点越重要。简单指标的优缺点对比如表1所示，这三个指标比较有代表性，且都具有较低时间复杂度。

表1 三个简单指标的相关信息

对简单指标进行归一化：

对于节点

v

的度值

(3)

对于节点

v

的点强

S

和

K

-shell值

Ks

，做同样的处理。综上所述，

n

个节点可以组成一个简单的指标值矩阵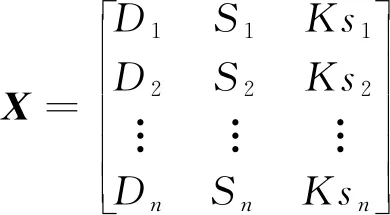

(4)

式中：为

n

个节点的度值、点强和

K

-shell值矩阵。

2 节点复杂指标

在复杂网络领域，辨识关键节点的方法主要包括社会网络分析方法和系统科学分析方法。

对于社会网络分析方法，可选取接近中心性与介数中心性作为评估指标。

接近中心性(

CC

)：计算网络中节点

v

与剩余节点的距离平均值，解决特殊值问题。若

v

与其他节点的距离比节点

v

小，则认为

v

的

CC

比

v

大。通常，最靠近中心的节点具有信息流的最佳视野。设网络包含

n

个节点，则

v

到网络中剩余节点的最短距离平均值：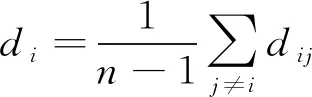

(5)

若

d

较小，则说明

v

比较接近网络的剩余节点。

d

的倒数可定义为节点

v

的

CC

：

(6)

CC

(

i

)越大，

v

越接近网络中心，位置越重要，重要性也越大。节点度和接近度方法效果对比如图2所示，可以看出：接近度比节点度更能精确区分节点重要性。

(a) 节点度 (b)接近度

介数中心性(

BC

)：在整体网络中反映节点的中心程度，节点

v

的介数

BC

(

k

)是指经过节点

v

的网络中全部节点对间的最短路径数占总最短路径数的比重。

(7)

式中：

σ

(

k

)为

v

与

v

间经由

v

的最短路径数目；

σ

为

v

与

v

间最短路径的数目。

对于系统科学分析方法，可采用节点删除法。节点删除法的思想是，删除某个节点后，计算网络性能，并与原网络比较，网络性能变化越大，节点就越重要。对于网络性能，采用网络连接密度与网络效率来衡量。

网络连接密度(

LD

)：在无权网络中，连接密度指网络中现有连边与可能存在的连边的比值。对于航空网络，可定义加权连接密度：

(8)

式中：

n

为当前网络节点总数；若

v

与

v

直接相连，

a

=1，否则，

a

=0；

w

为节点连边的权值。

LD

越大，整体的异质性越高，网络流量越大，网络综合性能越好。网络效率(

NE

)为所有节点之间的距离倒数和的平均值。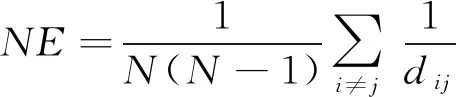

(9)

式中：

N

为网络中节点总数。

NE

反映了网络信息传输的难易程度，

NE

越大，信息传递越顺畅，抗毁性越强。

四个复杂指标的优缺点与时间复杂度对比如表2所示。

表2 四个复杂指标的相关信息

从表2可以看出：除了连接密度外，其余三个指标的计算时间复杂度均为

O

(

N

)。虽然综合上述四个指标能够较为全面地反映节点的重要性，但这样耗费时间较长，不适合复杂的大型网络。

3 核极限学习机(KELM)

考虑到航空网络节点训练样本集的复杂指标计算复杂度较高，提出采用基于核函数的ELM (Kernel ELM,简称KELM) 来学习简单指标与综合重要度之间的映射关系，以期耗费较少的计算时间和资源，实现航空网络节点重要度的准确评估，进而辨识出关键节点。

3.1 核函数理论

对于模式识别问题，当样本在低维空间线性不可分时，可通过某非线性函数映射到高维特征空间，能够实现线性可分。核函数基本原理：通过某非线性函数，将输入空间样本映射到高维特征空间，在高维特征空间进行数据的处理。其关键在于，引入核函数后，能够将高维特征空间的内积运算转化为输入空间内的运算。

设

x

与

x

为输入空间中的样本点，原始输入空间到高维特征空间的映射函数为

Φ

，则核函数方法可描述为实现内积变换(

x

·

x

)→

K

(

x

,

x

)= <

Φ

(

x

),

Φ

(

x

)>

(10)

式中：

K

(

x

,

x

)为核函数；<

Φ

(

x

),

Φ

(

x

)>为内积。在式 (10) 中，输入空间的核函数与高维特征空间的内积是等价的，非线性变换函数

Φ

的内积运算较为复杂，而核函数

K

(

x

,

x

)的运算则相对简单，因此，为了降低运算复杂性，可用输入空间的核函数运算替代高维特征空间的内积运算。此外，在使用核函数时，无需明确

Φ

的具体形式和参数，极大地方便了运算。核函数的映射过程如图3所示。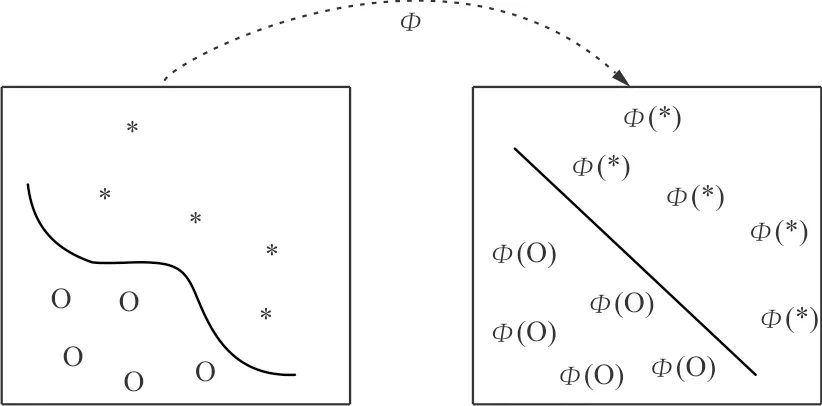

图3 核函数的映射过程

3.2 基于核函数的ELM

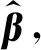
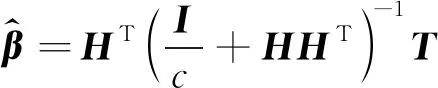
(11)

则ELM的输出函数为

(12)

对于训练样本(,)，且=[

x

1,

x

2,…,

x

]∈

R

与=[

t

1,

t

2,…,

t

]∈

R

，

g

()为激励函数，

L

为隐层节点个数(

L

≤

N

)。则ELM算法计算步骤：(1) 随机初始化输入层与隐层的权值向量和隐层节点偏置值

b

；(2) 构建隐层输出矩阵=[

g

(),…,

g

()]；

其中，=[

x

,

x

,…,

x

]，为

N

个样本；

g

()表示ELM网络隐层节点的输出函数，根据核函数理论，通过非线性函数将输入空间的样本点映射入特征空间，并由核函数代替特征空间的内积运算。假设隐层特征映射函数

g

()形式未知，则可用核函数代替其内积形式。ELM可通过核矩阵形式来描述

Ω

=∶

Ω

ELM,=

g

()·

g

()=

K

(,)

(13)

此时，基于核函数的ELM (KELM) 输出函数为

(14)

不难理解，在KELM算法中，无需了解

g

()的具体形式，仅需明确具体核函数

K

(,)，就可计算输出函数的值。需要说明的是，核函数为内积形式，在计算式 (12) 时，不需要确定网络隐层节点的个数。

4 节点重要度评估流程

本文提出采用KELM对航空网络节点重要度进行评估的流程如图4所示。

图4 节点重要性评估流程

具体可划分为以下四个步骤：

(1) 构造训练样本。从网络中随机生成部分节点，计算度值、点强和

K

-shell值等简单节点指标值；同时，确定接近中心性、介数中心性、网络连接密度和网络效率等复杂指标值。(2) 确定综合重要度。通过层次分析法(AHP)计算得出各复杂指标的权重：

W

=0.578 9;

W

=0.205 5;

W

=0.159 2;

W

=0.056 5，进而通过公式

Y

=0.578 9

BC

+0.205 5

NE

+0.159 2

CC

+0.056 5

LD

计算以上随机节点的综合重要度=[

Y

,

Y

,…,

Y

]。(3) 训练评估模型。以为输入，以为输出，训练KELM评估模型，以学习其内在关系。(4) 执行评估过程。对于网络中除训练样本的新节点，仅需计算新节点的简单指标，并输入KELM评估模型，就能计算出新节点的综合重要度，进而完成关键节点的辨识。此外，KELM训练时对参数变化反应比较敏感，当

c

值比较小，而

σ

值比较大时，模型的训练精度非常高，而测试精度却不理想，说明此时参数对训练的数据拟合程度非常高，但对新样本的预测能力却非常低，即出现通常所说的“过学习”现象。因此，在选取参数

c

和参数

σ

时，可引入交叉验证思想，计算出测试精度较高时所对应的最优参数组合。

5 仿真分析

为了验证本文所提方法的可行性，首先对随机网络进行测试，然后分别对中美两国航空网络进行测试，并对测试结果进行分析。

5.1 随机网络测试

考虑一随机网络

G

={

V

,

E

,

W

}，该网络含有600个节点，6 000条连边，实验目的是检验KELM关键节点辨识方法的有效性，也即判断KELM能够准确学习简单指标与综合重要度之间的关系。按照关键节点识别算法步骤，先随机选择60个节点作为KELM训练样本，通过AHP得出复杂指标

CC

、

BC

、

LD

和

NE

的权重分别为0.159 2,0.578 9,0.056 5,0.205 5，计算复杂指标加权，其和为综合重要度值

Y

，然后计算对应简单指标值

X

。KELM训练前，利用交叉验证法在log

c

∈[-10,10]与log

σ

∈[-10,10]内自动搜索最佳的参数

c

和参数

σ

，参数寻优过程如图5所示。图中，复杂指标重要度的实际值和预测值的均方根误差

RMSE

为

(15)

图5 对随机网络的参数寻优过程

从图5可以看出：网格图底部较平缓，说明在很大取值范围内的两个参数都可以使

RMSE

最小，因此，能够较容易地找出最佳参数

c

和

σ

。进行训练后，随机选择除训练样本之外的60个节点作为测试节点，计算得到其简单指标

X

，并输入KELM重要度评估模型，得到测试结果

Y

，与其原来复杂指标值评估得到的重要度

Y

进行比较，效果如图6所示。

图6 测试结果与实际值对比(随机网络)

从图6可以看出：KELM输出的结果与原来的重要度值非常接近，说明本文方法是准确、可行的。由表2可知，使用复杂指标对节点重要度评估所需时间复杂度为

O

(

N

)，而KELM评估仅需

O

(

N

)，其中，

N

为训练样本数。因此，采用这种方法，可以通过简单、耗时少的指标快速得到节点的综合重要度。

5.2 航空网络测试

对于美国航空网络，做同样测试，实验数据集包含332个机场节点、2 126条连边(直飞航线)以及连边的权重，美国航空网络的拓扑图如图7所示。数据来源详见文献[14]。

图7 美国航空网络拓扑

根据本文方法，通过交叉验证法确定参数，如图8所示。在节点重要度评估过程中，耗时最长的是知识数据库的建立(用复杂指标评估节点重要度)，如果选择网络中大部分节点作为训练样本，评估方法就失去了时间复杂度低的优势，变得没有意义。因此，本文测试KELM是否仅需要很少一部分节点就能准确评估节点重要度，分别随机选择20、40、60、80个节点作为训练样本，然后比较测试结果与原来的重要度值，如图9所示。

图8 对美国航空网络的参数寻优过程

(a) 20个训练样本

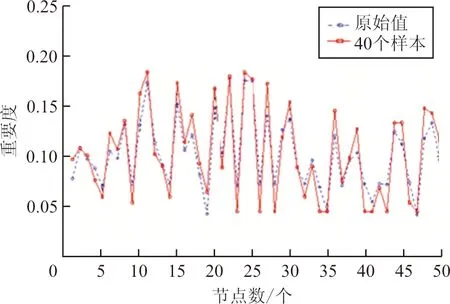
(b) 40个训练样本

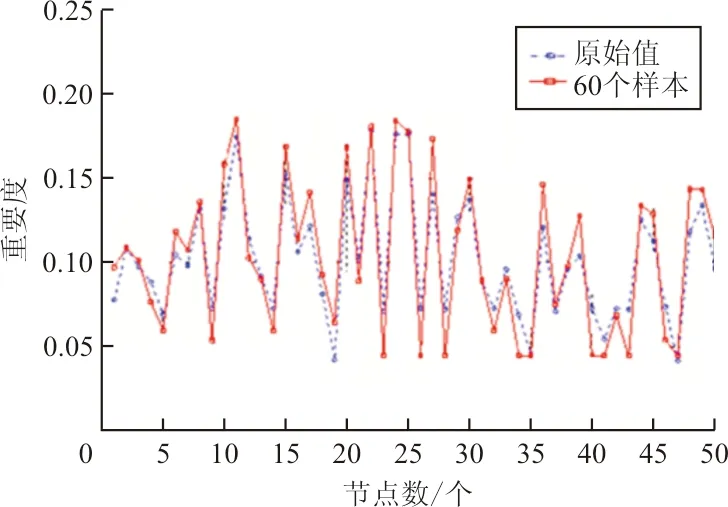
(c) 60个训练样本

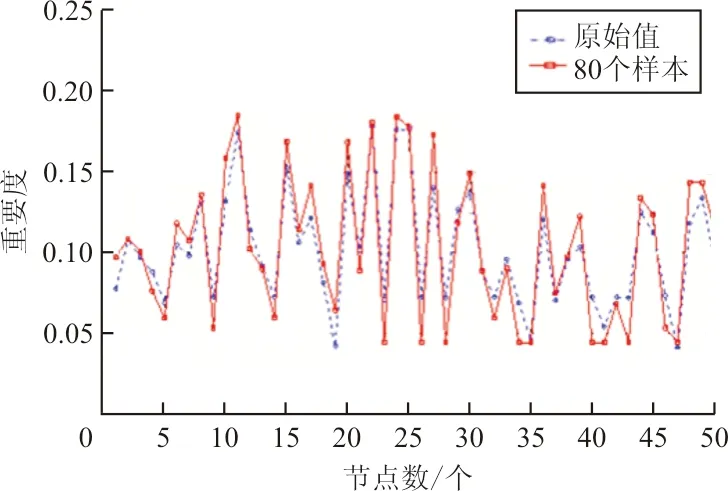
(d) 80个训练样本

从图9可看出：选择20个训练样本时，测试结果与原值的拟合效果较差，当选择40个训练样本时，拟合效果明显改善，选择60、80个节点时，拟合效果无明显提升。因此，在美国航空网络中，仅需计算40个节点的复杂指标值，如此将大幅降低原来的运算量，提高辨识关键节点的效率。

选择40个节点作为训练样本，对所有节点进行测试，得到测试结果后对节点进行排序，并与原复杂指标评估重要度排序、ACI排序进行比较，如表3所示。其中，ACI指国际机场委员会对美国各机场的综合排名。

表3 美国机场节点重要度排序

从表3可以看出：测试结果(简单指标评估结果)排名前16的机场节点与ACI仅有3个不同，说明本文方法比较符合现实情况，具有一定的准确性。再将测试结果与复杂指标评估结果作比较，发现两种方法的结果几乎一致，在前几名中，只有San Francisco与G.Bush对调了顺序，后几名略有差异，说明KELM的学习效果较好，具有准确预测数据的能力。

为了验证算法的通用性，把本文方法应用于中国的航空网络。将国内2016年199个具有定期航班的通航城市作为目标节点，爬取和收集网页数据，构建我国航空网络模型，并对我国航空网络进行关键节点识别。参数寻优过程如图10所示，检验测试结果的准确性如图11所示，可以看出：测试结果在趋势上与实际值总体保持一致。

图10 对中国航空网络的参数寻优过程

图11 测试结果与原值对比(中国航空网络)

6 结 论

(1) 基于接近中心性、介数中心性、网络连接密度对节点进行综合重要度评估，克服了以往复杂网络研究领域未考虑航线流量、机场位置等影响节点重要性的航空网络具体因素的不足。

(2) 采用KELM学习综合重要度值与简单指标的映射关系。对于剩余大部分节点，只需求出其简单指标，便可以求得其综合重要度和节点排序。解决了传统指标单一、未考虑边权的问题，提高了节点排序的准确性，同时降低了计算复杂度，节省了大量时间，实例验证了其有效性和可行性。

(3) 鉴于数据获取和时间问题，本文仅研究了民用机场构成的航空网络，在未来的研究中可以继续拓展，获取更加充实的数据，构建军航或者军民联合航空网络，以用于航空网络的平战转换机制研究。