一种面向边缘环境的多实例服务链在线部署算法*

宋 浒，甘让兴，夏 飞，邹昊东

(1.南京大学计算机软件新技术国家重点实验室,江苏 南京 210023;2.国网江苏省电力有限公司信通分公司，江苏 南京 210023)

1 引言

企业使用边缘计算技术将服务部署在离用户更近的边缘设备上，以满足用户对超低时延服务(虚拟现实[1]、流媒体[2]、自动驾驶[3]和图像处理程序[4]等)的需求。同时，虚拟化技术使网络功能脱离了专用硬件的束缚，能够灵活地部署在虚拟机和容器等设备虚拟实例上，大大降低了企业的成本，并且用户可以根据自身需求，将丰富的虚拟网络功能以服务链[5]的形式组合在一起，以提供不同的网络服务[6,7]，这极大地提高了边缘设备部署网络功能的灵活性和有效性。

但是，承载网络功能服务的边缘设备(无线路由器、网关等)通常只有有限的硬件资源[8,9]。例如，近年来发布的TP-LINK Archer C9无线路由器仅有1 GHz双核CPU[10]。面对不断增长的业务流量，这些资源有限的边缘设备极易发生过载现象。另外，随着物联网的高速发展，企业在城市周围部署了越来越多的智能设备，这些设备将收集大量的数据，导致在网络边缘处理的流量变化较大。智能设备上运行的应用程序流量模式的不同也会影响设备的负载。这些流量频繁变化的用户请求同样会造成边缘设备过载。

为了应对边缘设备过载问题，首先需要对服务链的资源消耗进行精准的测量。服务链的资源消耗主要指网络功能计算所需要的资源消耗。文献[11]表明，数据包传输在边缘设备上会消耗大量的资源，而已有工作通常忽略这类资源消耗。本文对服务链负载模型进行了细粒度建模，充分考虑了网络功能计算和数据包传输2种类型的资源消耗。相比已有的研究，本文设计的负载模型对服务链中多实例的资源消耗进行了更准确的建模。面向边缘环境的多实例服务链部署模型，包括边缘设备负载模型和基于虚拟实例通信的时延约束模型2个组成部分。在此基础上形式化地描述了最小化最大边缘设备CPU负载率的最优化问题。

基于细粒度的服务链负载模型，本文证明了多实例服务链在线部署问题为NP难问题。因此，为了能在满足时延约束的情况下，在边缘环境进行多实例服务链的部署，以期望达到边缘环境下边缘设备间负载均衡的效果，本文设计了面向边缘环境的多实例服务链在线部署算法。该算法包括3个阶段：(1)时延满足路径搜索:查找当前网络拓扑下满足时延约束的路径集合；(2)部署路径选择:选择路径集合内的一些路径部署服务链；(3)网络功能部署:将服务链的网络功能按照用户要求的部署策略部署在优选的路径集合内的边缘设备上。

仿真实验表明，该算法在最大边缘设备CPU负载率这一评价指标上优于忽视服务链网络功能间存在通信开销的基准算法。通过对比小规模网络拓扑的最优部署结果，该算法结果接近最优部署结果。

本文的组织结构如下：第2节通过路由器容器部署实验分析影响网络功能实例的CPU负载的因素；第3节对多实例服务链在线部署问题进行建模；第4节对部署问题进行算法设计；第5节对部署算法进行评估；第6节对本文内容进行总结。

2 容器化网络功能通信开销

为了应对边缘设备过载问题，本文首先对提供服务的服务链网络功能的资源消耗进行细粒度的测量。本文在无线路由器内通过容器化部署服务链设计了一个基准实验。实验中使用了一个无线路由器和一台服务器。无线路由器中部署虚拟网络功能链，服务器同时作为流量的发送方和接收方。该实验将服务链的网络功能设置为数据包转发过程，忽略网络功能计算资源的消耗，从而得到数据包在网络功能间传递的通信开销。通过调整服务链长度、数据包速率和数据包大小3个关键参数，同时持续读取无线路由器CPU利用率，得到CPU利用率与3个参数的关系。通过控制变量的方式。分别分析了CPU利用率和服务链长度、数据包速率和数据包大小的关系，实验结果如图1所示。图1中采样点代表实验数据，通过最小二乘法得到拟合线(未进行实验时，无线路由器的CPU利用率为1%～2%，所以拟合线未过原点)。

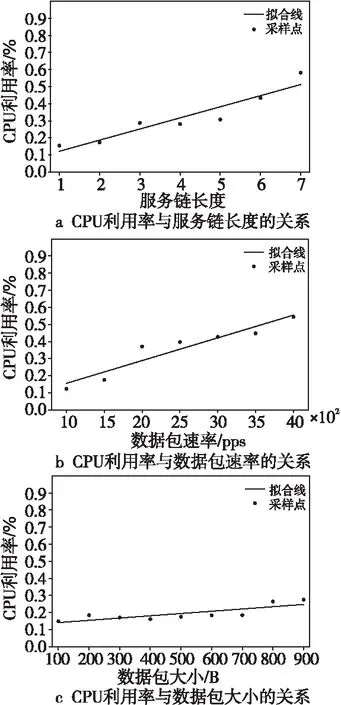
Figure 1 Relationship between CPU utilization and service chain length, packet rate and packet size

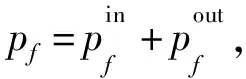
load(T)=comm(T)+comp(T)=

(1)

其中，αf是网络功能f计算开销和通信开销的比率。注意到，该模型不同于传统的仅考虑计算开销的服务链负载模型(简称为服务链负载传统模型)：

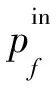
(2)

另一方面，为了降低设备的负载，提高服务的稳定性，通常会在不同设备的虚拟实例内部署同一网络服务[12-14]，在对用户流量进行划分后通过部署某个网络功能的多个虚拟实例实现负载均衡。但可惜的是，目前缺乏结合上述2个方面的服务链部署算法研究工作。因此，本文设计并实现了一种面向边缘环境的多实例服务链在线部署算法，在现有的边缘环境下，提供低时延、低负载的网络功能服务。

3 多实例服务链在线部署问题建模

在边缘环境下存在着大量的边缘设备，这些边缘设备的CPU和内存资源使用情况各不相同。企业可以使用这些边缘设备，将服务链中的网络功能部署在具有较低负载和较近距离的对等边缘设备上，提供低时延的服务，同时缓解设备过载的问题。本节在模型假设的基础上，首先对边缘环境进行建模；然后通过虚拟实例通信图来描绘多实例服务链部署的通信情况；接着，提出了衡量设备负载的边缘设备负载模型和概括服务链时延约束的时延约束模型；最后，给出了问题求解的目标函数和难度论证。

3.1 模型假设

由于边缘设备的资源有限性，本文假定虚拟实例以容器的方式部署在边缘设备。为了简化边缘环境模型，本文采用如下假设：

(1)边缘设备上运行的容器可以部署任意类型虚拟网络功能VNF(Virtual Network Function)。

(2)任何虚拟实例只能部署一个虚拟网络功能。

(3)仅关注边缘设备之间的传播时延，不考虑设备内部处理流量导致的传输时延。

3.2 边缘环境模型

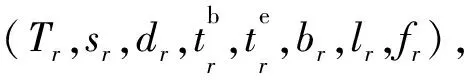
由于VNF实例可能改变通过该功能的流量大小，例如IPSec/SSL VPN和媒体网关会将通过的数据包进行封装和解封装操作而改变数据包的大小[15]；防火墙和入侵检测系统会丢弃违反安全策略的数据包而改变数据包的数量[16]。本文定义αTr,i表示服务链第i个网络功能改变流量的比率，βTr,i表示服务链第i个网络功能计算开销和通信开销的比率。由于单位时间间隔内存在多个用户部署服务链的情况，所以本文用符号N表示单位时间间隔内用户请求的数量，并将时间间隔t内，对边缘设备有负载作用的用户请求集合表示为R(t)。边缘设备v的负载容量表示为Cv。本文使用|X|表示集合[X]的大小，例如，符号|Tr|表示服务链长度，|Tr,i|表示部署服务链第i个网络功能的实例个数。

3.3 虚拟实例通信图

为了降低设备的负载，提高服务的稳定性，通常将服务链的网络功能部署在多个边缘设备容器中。虚拟实例通信图能描绘服务链部署的情况。如图2所示，圆形代表边缘设备，方形代表虚拟实例，箭头上方数字代表流量大小。例如，虚拟实例Tr,1,1和虚拟实例Tr,2,1有通信关系，而和虚拟实例Tr,2,2没有通信关系。

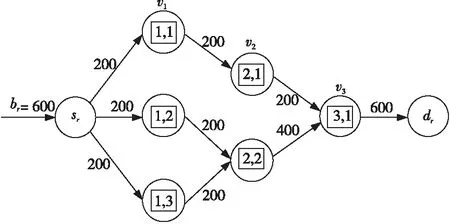
Figure 2 An example of virtual instance communication graph

软件定义网络技术可以通过下发流表项到边缘设备的方式调度用户网络流通过特定虚拟实例。但是，受网络流数量|fr|的影响，部署服务链第i个网络功能的虚拟实例个数需满足以下不等式：

|Tr,i|≤|fr|,i∈[1,|Tr|]

(3)

等号成立当且仅当部署服务链第i个网络功能的虚拟实例运行在完全不同的边缘设备上。从图2中可以看出，用户请求从某网络流的源节点出发，依次通过运行在边缘设备v1、v2和v3上的VNF实例，最终到达目标节点。

3.4 边缘设备负载模型

为了达到边缘设备间负载均衡的目标，本文需要对边缘设备的负载情况进行建模。部署服务链第i个网络功能的虚拟实例的入口流量和出口流量的关系为：

(4)

由于信道不会改变流量大小，所以由流量守恒可知，部署服务链第i个网络功能的虚拟实例j的入口流量等于和该虚拟实例有通信关系的部署第i-1个网络功能的虚拟实例的出口流量之和：

(5)

其中，hTr,i-1,k,i,j∈{0,1}是通信二值变量，当hTr,i-1,k,i,j=1时，表示部署服务链第i-1个网络功能的虚拟实例k和部署服务链第i个网络功能的虚拟实例j有通信关系；否则，hTr,i-1,k,i,j=0。另一方面，初始带宽等于部署服务链第1个000网络功能的虚拟实例的入口流量之和：

(6)

在时间间隔t内，部署服务链第i个网络功能的虚拟实例j的入口流量和边缘设备v的关系为：

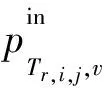
(7)

其中，xt,Tr,i,j,v∈{0,1}被称为设备二值变量，当xt,Tr,i,j,v=1时，表示在时间间隔t内，部署服务链第i个网络功能的虚拟实例j运行在边缘设备v上；否则，xt,Tr,i,j,v=0。同理，在时间间隔t内，部署服务链第i个网络功能的虚拟实例j的出口流量和边缘设备v的关系为：

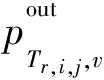
(8)

基于服务链网络功能间存在通信开销的服务链负载模型，在时间间隔t内，边缘设备v的负载为：

loadv(t)=∑r∈R(t)((ω+αTr,i)·

(9)

同理，在服务链负载传统模型下，在时间间隔t内，边缘设备v的负载为：

(10)

3.5 时延约束模型

边缘环境模型规定的流量必须通过源节点和目标节点。为了统一时延约束表示，本节为服务链添加2个不增加负载的网络功能Tr,0和Tr,|Tr|+1，并将其分别置于服务链的首端和尾端(保持服务链长度不变，通过额外下标表示这2个假设的网络功能)，而且人为规定部署网络功能Tr,0的虚拟实例必须运行在源节点上，部署网络功能Tt,|Tr|+1的虚拟实例必须运行在目标节点上，由式(11)表示如下：

(11)

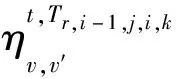
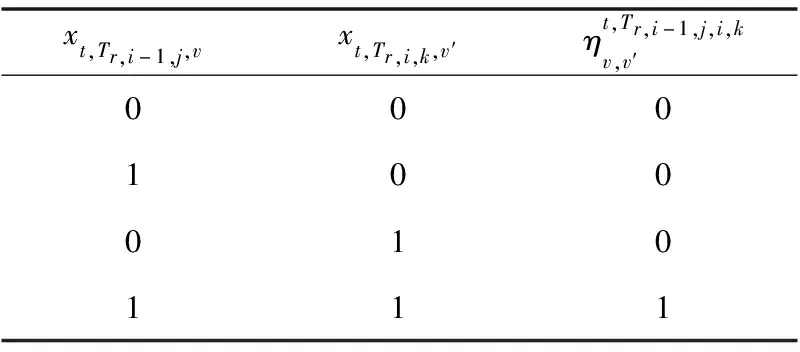
Table 1 Constraint relationship between equipment binary variable and delay binary variable

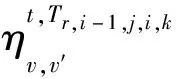
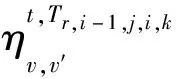
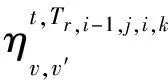
∀t,∀r∈R(t),∀v,v′∈V,hTr,i-1,j,i,k=1

i∈[1,|Tr|+1],

j∈[1,|Tr,i-1|],k∈[1,|Tr,i|]

(12)

综上可以得出，服务链的时延约束满足不等式：

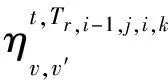
∀r∈R(t),hTr,i-1,j,i,k=1,i∈[1,|Tr|+1],

j∈[1,|Tr,i-1|],k∈[1,|Tr,i|]

(13)

3.6 目标函数

s.t. (3)～(9),(11)～(13)

(14)

该目标函数F旨在时延约束以及所有时间间隔内，最小化最大边缘设备CPU负载率，即对边缘环境下的边缘设备进行负载均衡。

求解该问题存在2个难点：(1)由于边缘环境下用户的移动性，用户请求会频繁加入和退出，不同于服务链的静态部署，最大边缘设备负载和时间维度有关；(2)边缘设备的负载均衡问题必须同时考虑时延约束和网络功能的负载差异性。一方面，时延约束限定了对等边缘设备的选取；另一方面，网络功能负载的差异性增加了在对等边缘设备间保持负载均衡的难度。

3.7 NP完全性证明

首先，问题能在多项式时间内验证候选解是否满足约束条件。其次，本节首先简短介绍已被证明为NP完全问题的多处理器调度MPS(Multi-Processor Scheduling)问题[17]，然后证明MPS问题可以归约到F的一个子问题F1，该子问题是面向边缘环境的只考虑计算开销的线性服务链部署问题。

MPS：给定n个任务J={J1,J2,…,Jn}，每个任务需要pj时间去处理；m台机器M={M1,M2,…,Mm}(n>m)，由这m台机器来完成这n个任务。如何调度这些任务，使得最后完成所有任务的时间最短。

定义F1：在保持F其它条件不变的情况下，改变以下4个条件：

(1)用户请求r流量内网络流数量|fr|为1。

(2)时间间隔数量TN=1，且用户请求数N=1。

(3)忽略服务链网络功能间的通信开销，即commTr,i=0。

(4)时延约束lr被设定为无穷大。

下面证明F1是NP难问题：

证明构造规约过程如下，将MPS问题的输入构造成子问题的输入，即服务链具有n个网络功能，每个网络功能会产生pj的计算开销，边缘环境下有m个边缘设备。为达到设备间负载均衡当且仅当所有边缘设备的负载情况相同。已知MPS问题的输出，即所用时间最短当且仅当所有机器的处理时间相等。由于边缘设备和机器具有一一对应关系,且在子问题以及MPS问题的输出中,任意边缘设备的负载和对应机器的处理时间在数值上相等。因此，在多项式时间内，MPS问题的输入可以转换成子问题的输入，且子问题的输出可以转换成MPS问题的输出，证毕。

□

该证明说明子问题F1是NP难问题，进而F是NP难问题，从而F是NP完全问题，除非能证明P=NP，否则不可能为F找到一个高效的多项式算法，基于求解问题F的难度论证，本文将在下一节中给出一个启发式算法DS-PC-ND(Delay Statisfaction-Path Collection-Network function Development)去解决该问题。

4 DS-PC-ND算法设计

4.1 DS-PC-ND算法框架

为了能在满足时延约束的情况下，在边缘环境进行多实例服务链在线部署，以期望达到边缘环境下边缘设备负载均衡的效果，算法框架分为如下3个阶段：

(1)阶段1(时延满足路径搜索)：搜索当前网络拓扑下满足时延约束的路径集合P1。

(2)阶段2(部署路径选择)：选择路径集合P1内的|fr|个路径组成路径集合P2作为部署路径集合。

(3)阶段3(网络功能部署)：将服务链的网络功能按照某种部署策略部署在路径集合P2的边缘设备上。

这3个阶段表明多实例服务链的部署涉及到将服务链分配到满足时延约束的若干路径(P2)上，并将服务链的网络功能部署在路径中资源较为充足的边缘设备上。需要说明的是，由于网络流数量|fr|不等于|P1|，所以阶段2在时延约束路径集合P1内选出部署路径集合P2，这能简化阶段3内网络功能部署的过程。算法框架如图3所示。下面小节将依次介绍时延满足路径搜索DS(Delay Statisfaction)算法、部署路径选择PC(Path Collection)算法和网络功能部署ND(Network function Development)算法。

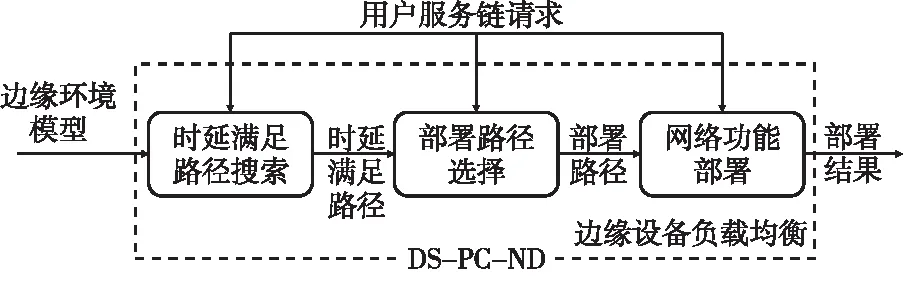
Figure 3 Framework of DS-PC-ND algorithm

4.2 时延满足路径搜索算法

由于边缘环境模型假定用户请求必须通过已知的源节点和目标节点，所以时延满足路径搜索可以看成在已知源节点和目标节点的情况下，找出满足时延约束lr的路径集合P1。为了降低问题的难度，本文假定时延满足路径搜索(DS)算法搜索的是简单路径，即路径中的节点不能出现重复，这样得到路径集合P′1，显然P′1⊂P1。

本文使用双栈数据结构设计了一个基于剪枝搜索策略的非递归算法去求解时延满足路径搜索问题。如算法1所示，该算法首先准备2个栈(主栈S1和辅栈S2)，主栈中的每个元素是单个值，表示当前路径的某个节点，辅栈中的每个元素是一个列表，表示主栈对应元素的邻接节点集合，即主栈记录的是某一条以源节点为起点的路径，而辅栈记录主栈路径可能的下一跳。本文使用变量时延和delay来记录目前主栈路径的时延之和。当主栈栈顶元素为目标节点时，主栈栈底到栈顶的元素序列记为符合时延约束的一条简单路径。为了使选择出来的路径是简单路径，算法1保证主栈压入的下一跳不会和主栈已有元素重复。函数Neig返回邻接节点列表；函数First返回列表第1个元素；函数Remain表示将列表第1个元素去除后，组成一个新的列表；函数Seq返回栈底到栈顶元素序列；函数Delay返回2个节点之间的时延；函数RmRp(X,Y)去除列表X内Y包含的元素。

算法1时延满足路径搜索算法

输入：图G(V,E)，用户请求。

输出：满足时延约束的简单路径集合P′1。

S1←sr，S2←Neig(sr)；

Repeat

neigs←S2.pop()；

If!neigs.empty()then

S2.push(Remain(neigs))；

next←Delay(S1.top(),First(neigs))；

Ifdelay+next≤lrthen

delay+=next；

S1.push(First(neigs))；

S2.push(RmRp(Neig(S1.top()),S1))；

Endif

Else

S1.pop();continue；

Endif

IfS1.top()==drthen

P′1.push(Seq(S1))；

delay-=Delay(S1.top(),S1.nextTop())；

S1.pop();S2.pop()；

Endif

UntilS1.empty()；

ReturnP′1；

4.3 部署路径选择算法

通过时延满足路径搜索算法，本文找到满足时延约束的简单路径集合P′1。由于本文设定用户请求内网络流流通的路径是固定的，且网络流数量为|fr|，所以需要在P′1内选择|fr|条路径来作为部署服务链的部署路径集合P2。但是，为了降低时间复杂度，本节使用嵌套TopK策略在路径集合P′1中找出将要部署多实例服务链的路径集合P2。本文将该算法称为部署路径选择(PC)算法，其具体实现包含嵌套函数(函数1嵌入函数2内，作为函数2的一条语句执行，函数2返回最终的部署路径集合P2)。

函数1内容说明：对于p∈P′1，本函数选取路径p内负载最小的K1(|Tr|)个边缘设备来代表路径p内所有边缘设备的负载情况，并将这K1个边缘设备负载和的均值记为loadp，并将该值返回给函数2。

函数2内容说明：由于总共有|P′1|条路径，而本函数的目标是选择出|fr|(记为K2)条路径作为部署路径集合P2(该集合是算法3的输入)，而一般情况下|P′1|都不等于|fr|，所以需要设计一种策略在P′1中选择|fr|条路径。本文设定函数2使用函数1返回的loadp值来进行选择，即选取P′1内loadp值最小的|fr|条路径(loadp值和p存在一一对应关系)。

基于嵌套TopK策略中，函数1和函数2包含嵌套关系，并且函数1和函数2的运算过程涉及到选择K个元素(函数1中K=K1，函数2中K=K2)。

算法2部署路径选择算法(函数1)

输入：时延满足路径集合P′1，用户请求r，边缘环境模型。

输出：部署路径集合P2。

初始化最大堆D1；

进入函数1(p由函数2传递给函数1)；

Foreachnode∈pdo

IfD1.top()>Load(node)then

D1.pop()，D1.push(Load(node))；

Endif

Endfor

loadp←D1内有效元素和的均值；

重置D1；

Returnloadp；

本文使用堆来处理TopK选择问题，使用了2个最大堆D1和D2。维持D1大小为|Tr|，维持D2大小为|fr|。显然，很容易得到函数1的时间复杂度为O(|p|·log2(|Tr|))，函数2的时间复杂度为O(|P′1|·log2(|f4|))，但由于函数1要运行|P′1|次，所以算法2的时间复杂度为O(|P′1|·|p|·log2(|Tr|)+|P′1|·log2(|fr|))。另一方面，由于算法2需要维护2个最大堆，所以该算法的空间复杂度为O(|Tr|+|fr|)。

4.4 网络功能部署算法

得到了将要部署多实例服务链的简单路径集合P2后，本节设计了一个基于贪心策略的启发式算法将多实例服务链的网络功能部署在这些路径上的边缘设备上。如算法3所示，对于每一条部署路径p∈P2，部署算法首先找到该路径的最小负载节点node，然后将服务链的第1个网络功能部署在该节点上,之后将部署路径p的起点设置为node。如此往复，直至服务链的全部网络功能部署完毕。

算法3网络功能部署算法

输入：部署路径集合P2，用户请求r，边缘环境模型。

输出：部署结果。

Foreachp∈P2do

ForeachTr,i∈Trdo

获取p内最小负载节点node；

更新边缘设备node的负载；

将p的起点设置为node；

Endfor

Endfor

算法3的时间复杂度为O(|P2|·|Tr|·|p|)，因为该算法包括2层循环，外层循环要进行|P2|次，内层循环要进行|Tr|次，内层循环中查找最小负载节点要对路径p遍历一次(时间复杂度为O(|p|))。该算法只使用常数个额外变量，空间复杂度为O(1)。

5 DS-PC-ND算法评估

对于多实例服务链在线部署算法DS-PC-ND，本文将从2个方面来评估其性能：一方面，由于服务链网络功能间存在通信开销，所以希望知道该算法能多大程度缓解负载失衡现象；另一方面，评估该算法与最优部署结果之间的差距。

5.1 仿真环境与仿真参数

仿真实验在Linux环境下进行，使用LEMON网络仿真库[18]随机生成2个网络拓扑。网络拓扑A包含30个节点和47条边，网络拓扑B包含6个节点和7条边。对于每个用户请求，本文随机从所有节点中选择源节点sr和目标节点dr，并保证sr和dr不会重复。同时，假定用户请求r的网络流均分初始流量br。仿真参数如表2所示。其中，[X′,Y′]表示仿真参数随机且均匀地从X′～Y′中生成，{I,J}表示仿真参数随机地从I～J中生成(取整数)。另外，本文将单位时间间隔设定为1 s，为了研究单位时间间隔内用户请求数N对设备负载的影响，本文将N设置成不同数值后进行仿真实验。为了避免设定固定数值的时延约束lr对算法评估的负面影响，本文将时延约束lr设定为sr到dr的最短路径时延和的2倍。

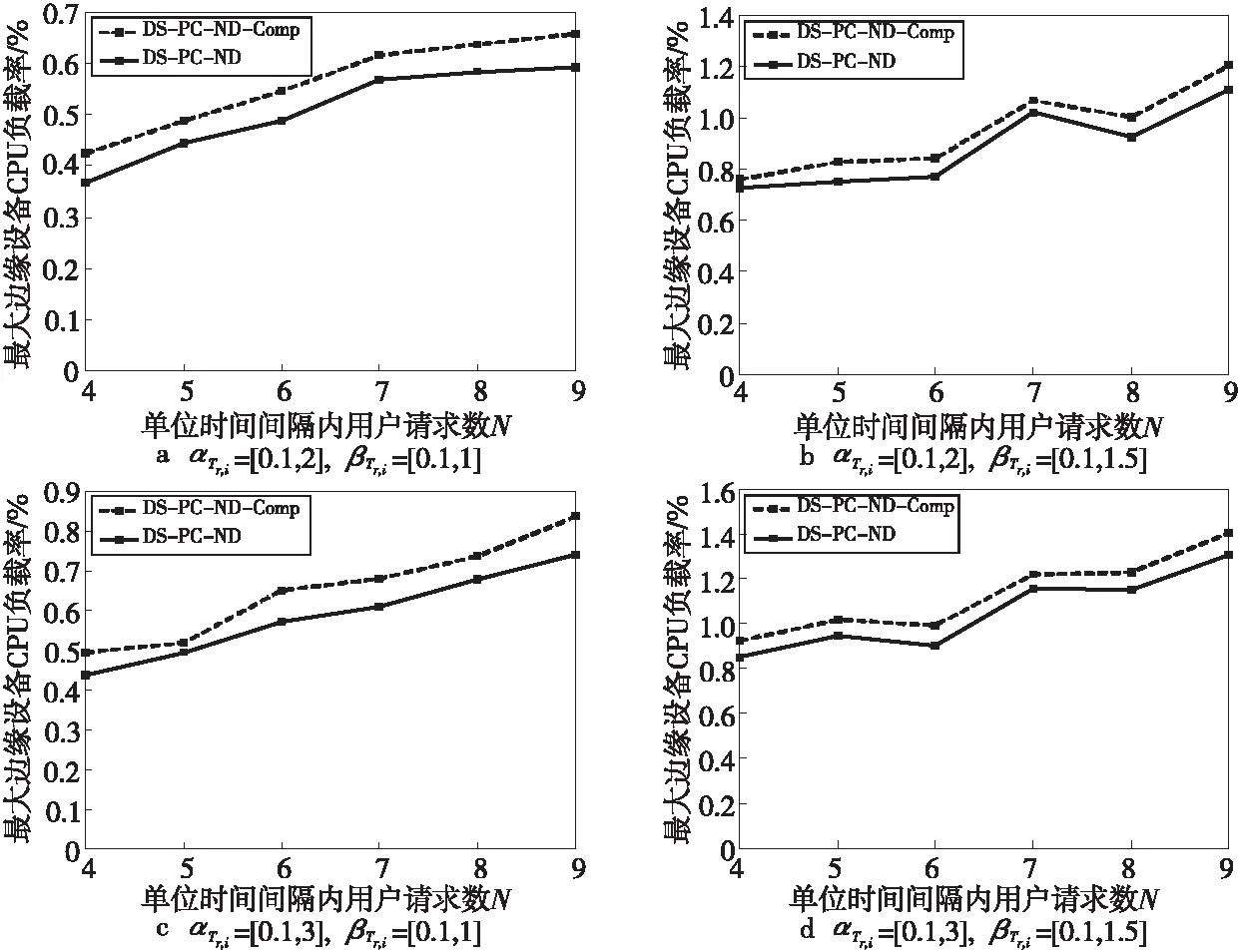
Figure 4 Comparison of DS-PC-ND and DS-PC-ND-Comp

5.2 评价指标

评估问题的目标函数为最大边缘设备CPU负载率，即对最大的边缘设备CPU负载进行归一化后的结果。显然，最大边缘设备CPU负载率值越低，说明算法性能越好。

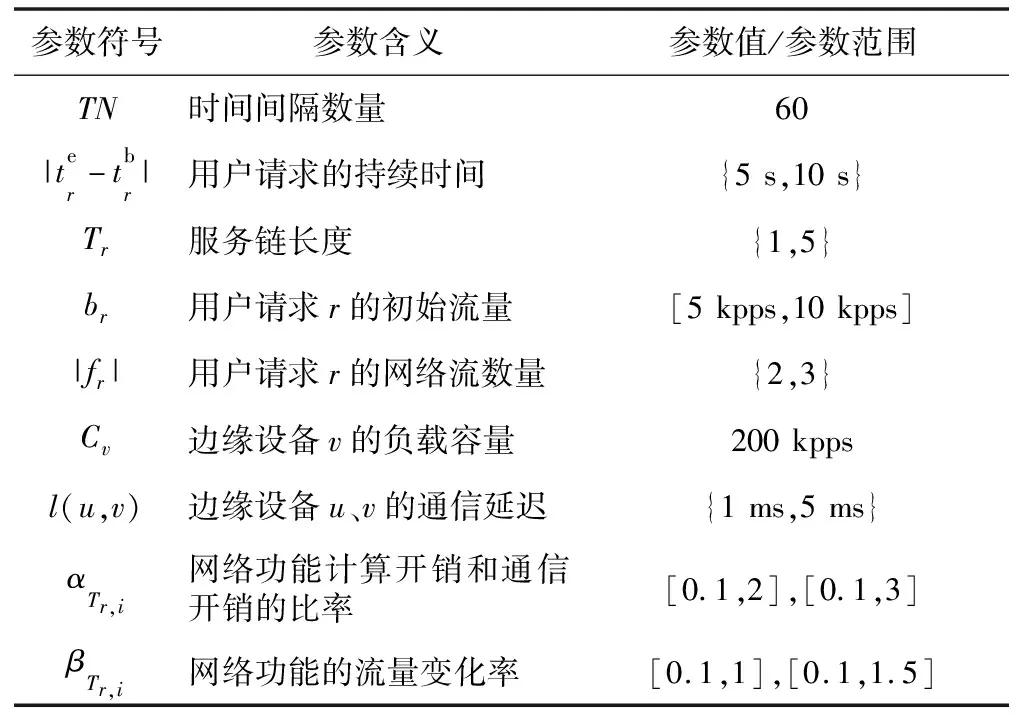
Table 2 Simulation parameter table

5.3 基准算法

基准算法DS-PC-ND-Comp是为验证服务链网络功能间通信开销对边缘设备负载均衡的影响而设计的。具体算法如下所示：保持DS-PC-ND算法框架不变，将服务链负载模型由服务链负载事实模型替换为服务链负载传统模型，即认为服务链网络功能间只存在计算开销，并基于该认识去运行部署路径选择算法和网络功能部署算法。

5.4 DS-PC-ND vs.DS-PC-ND-Comp

本节将评估DS-PC-ND算法相对于基准算法DS-PC-ND-Comp的优势，以验证忽略服务链网络功能间存在通信开销这一事实的不良影响，对比结果如图4所示。可以看出，DS-PC-ND算法优于基准算法DS-PC-ND-Comp 3%～10%个单位边缘设备CPU负载率。

更具体地说，图4a和图4b的βTr,i设置不同，这使得图4b中通过网络功能的流量可能变大，这增加了边缘环境的流量总量，使得最大边缘设备CPU负载率变大，同理可得图4c和图4d的结果对比；图4a和图4c的αTr,i设置不同，这增加了图4c中服务链的计算开销占比，使得最大边缘设备CPU负载负载率变大，同理可得图4b和图4d的结果对比。

5.5 DS-PC-ND vs.Optimal

本节将评估DS-PC-ND算法和基于最优化方程求解的最优部署结果Optimal(使用规划问题求解器Gurobi求解)的差距。为了降低求解最优部署结果的问题规模，本节将边缘环境网络拓扑修改为网络拓扑B。在多个时间维度(TN=10,TN=20)下进行了仿真实验，实验结果如图5所示。

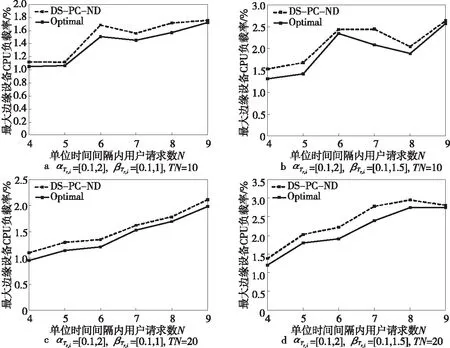
Figure 5 DS-PC-ND vs.Optimal

从图5可以看出，DS-PC-ND算法的部署结果接近最优部署结果，这是由于部署路径选择算法尽可能选择负载较小的部署路径，而且网络功能部署算法也尽可能地将网络功能部署在负载较小的边缘设备上，这些启发式策略能保证接近最优部署结果。

6 结束语

在基于服务链网络功能间存在通信开销以及服务链网络功能同时部署在多个虚拟实例内这2个事实基础上，本文对面向边缘环境的多实例服务链在线部署问题进行了建模，并提出了一个3阶段算法DS-PC-ND进行求解。仿真实验结果表明，该算法缓解了设备间的负载失衡现象，并且接近最优部署结果。由于该算法中包含启发式算法，因此未来还有比较大的改进空间。