基于3D视觉的散乱堆放工件机器人抓取技术研究*
2021-03-01崔旭东王平江余凌波陈吉红
崔旭东 谭 欢 王平江 余凌波 陈吉红
(①鞍山师范学院计算中心,辽宁 鞍山 114007;②华中科技大学机械科学与工程学院,湖北 武汉430074)
机器视觉因其具有适应性好、柔性强、非接触等特点,被广泛用于自动化生产线的工件尺寸检测、缺陷检测以及分拣中。使用机器视觉进行测量并配合多关节机器人进行工件的分拣,可以提高作业效率,降低工人作业的劳动强度。在自动化生产线中,零部件的抓取及安放,是一个非常重要的环节,也是目前自动化产线消耗人力最大的一个环节。有些类型的工件,若使用机械振动分拣装置,不仅可靠性低,而且振动噪声非常巨大,严重影响工人的身体健康[1]。
随着企业越来越重视柔性化、自动化制造技术的应用,采用基于三维视觉的机器人技术,对散乱堆放的工件进行自动、高效的分拣,其需求越来越迫切,应用也越来越受到重视。从散乱堆放的料框中分拣出单一工件并按照要求的姿态摆放到指定的上料工位,若使用人工的方式进行,枯燥乏味还浪费人工。使用机器视觉技术进行散乱堆放工件的位置姿态检测,再规划机器人抓取的轨迹及抓取的位姿,具有柔性化程度高、缓解企业用工压力、无环境影响、24小时作业的优点[2-3]。
本文针对散乱堆放工件的基于机器视觉的机器人分拣技术的难点,进行了有益探索,提出了切实可行的解决方案。
1 三维视觉测量原理简介
为了能够精确地重建料框中散乱堆放工件可视面的三维点云数据,本文采用双目立体视觉加结构光格雷码[4-5]、相位移的方式[6],进行三维点云数据的获取。双目测距的基本原理[7]如图1所示,依据图1中的相似三角形,可以得到公式:
(1)
(2)

图1中,OR、OT分别为左、右相机成像主光点。左、右相机成像感光平面到其各自光心的距离均为焦距f。若P为三维空间中某待测的目标点,P在两个相机成像平面中的成像点分别为p和p′;p和p′到各自成像平面左侧边缘距离分别为xR和xT;B为左右两个相机间的基线长度,则Z为P点到基线的距离即为双目3D视觉测量所得点的空间位置。
图2为整个三维视觉测量系统硬件构成,包括:两个工业相机1、数字激光投影的面结构光投影仪2、六轴机器人3以及存放工件的料框4。散乱堆放工件可视面三维测量过程为,首先用DLP投影仪依次将若干幅格雷码图像与4幅相位移图像,投影于散乱堆放的工件表面。同时用相机依次采集工件可视面成像图像,如图3所示,即可根据格雷码编码规则、相位移移相规则及立体视觉的极线约束原理,确定左右相机拍摄的空间同一点P在左右相机图像上点(p,p′)的对应关系。


根据文献[6-7]所述双目测量原理,计算视场中众多工件表面的三维点云数据。对散乱堆放的工件进行测量所重建的三维点云效果如图4所示。

2 目标工件分割及三维匹配方法
2.1 三维匹配用模型点云生成
要确定散乱堆放的某工件位姿,首先须获得用于进行三维匹配的模板点云Ω0,再将Ω0与料框中已测量且已经分割的目标工件三维重建点云Ωi进行三维匹配,最后得到散乱堆放在料框中的目标工件的位置以及姿态信息。
获得工件三维匹配的模板点云Ω0有两种方式。如图5所示为从生产单位获得的工件的CAD理论模型,经离散处理得到的整个工件外表面的点云数据;图6为通过本文研发的三维测量系统对单个工件实物进行现场测量、重建、拼接而形成的模板点云数据。虽然通过CAD模型生成的模板点云Ω0,具有更好的细节表现,但是通过现场测量得到模板三维点云Ω0的方法,具有使用简单、操作方便的优点。本文研究表明,两者在三维匹配中的匹配精度及使用效果基本相同。


2.2 目标工件分割算法
从一堆散乱堆放的工件的三维点云中进行目标工件的分割,目前还没有很好的方法。考虑到本测量系统采用的是双目视觉,并通过多幅序列图像而进行的重建,且投影仪的投光模式是可控的,因而可以通过投射一幅均匀的、强度可控的照明光源,获得散乱堆放状态下工件的二维图像。再通过对该二维图像的分割,将二维图像划分成不同的区域,那么在三维场景中也将对应二维图像区域的三维点云进行不同的划分,从而可以大致区分出属于不同工件个体的三维点云数据子集。从二维图像出发,对料框中的散乱工件进行分割,是减少三维空间分割算法复杂性、提高三维匹配效率的可行方法。
常见的二维图像分割算法有二值化法、分水岭法[8]、边缘法[9-10]等。图7所示为测试图像采用边缘法分割处理的结果。本文采用该方法对料框中散乱堆放的工件进行二维图像上的分割,以初步确定目标工件及其所属的三维点云子集。
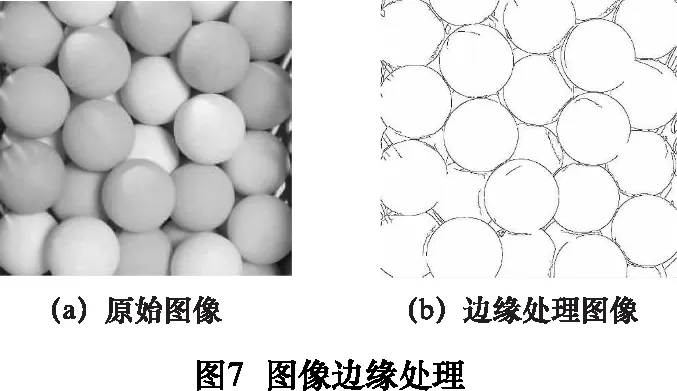
2.3 三维匹配算法
三维点云之间的匹配已有多种实现方法,如特征点匹配[11-12]、ICP(iterative closest point)匹配[13-14]等。
特征点法主要通过三维点云的局部点云分布情况,确定该子区域的特征子。比对目标以及模板的特征子,查找最接近的组合,进一步求解得到目标与模板点云之间的空间刚体变换矩阵。特征点匹配速度上较快,但是如果特征点较少或者特征点分布在无关区域(例如工件边界处),则容易产生匹配失效的情况[15]。
ICP匹配,是一种通过最近距离原则确立匹配点对,迭代计算出目标点云与模板点云之间的三维刚体空间变换矩阵的算法[16]。
使用ICP算法时,通常需要使用PCA(principal component analysis)方法[14],以获得良好的初始位姿,从而提高ICP配准的速度与准确度。PCA姿态变换过程如下:
若点云由m个点构成,设X是包含所有点坐标的3×m矩阵;点云的重心坐标为μ。首先,需要对点云进行平移,新坐标系的坐标原点为点云的重心μ,平移变换后得到点云新的3×m矩阵Xμ。通过构造协方差矩阵covX,并获得covX最大特征值对应的特征向量,进一步构造正交且满足右手系规则的旋转变换矩阵R;使用旋转变换R对Xμ进行旋转变换,得到Xout。Xout为先平移再旋转变换后包含所有点坐标的3×m矩阵。如图8所示,为PCA变换的概念及其结果,其中“·”为变换前的点云,“*”为变换后的点云。PCA变换后,点云的重心为新坐标系原点并且主成分方向与原坐标系X坐标轴方向一致。
Xμ=X-μ
(3)
(4)
Xout=R×Xμ
(5)

模板点云Ω0及目标点云Ω1,是都经过PCA变换后的点云(此时模板点云Ω0及目标点云Ω1都是在各自的重心坐标系下进行描述的),再进一步进行ICP匹配,即可得到最终的三维点云位姿匹配结果。ICP匹配过程如下:
(1)采用最近距离原则得到模板点集M= {qi}(i=1,2,3,…,L)与目标点集S= {pj}(j=1,2,3,…,K)中对应点关系,得到一一配对的点的集合{(q1,p1);(q2,p2);…;(qi,pi)…;(qN,pN)}。图9中“·”为目标点集S,“*”为模板点集M,连线表示点之间的配对关系。配对后N≤min(L,K)。R,T为目标点集与模型点集之间的旋转变换矩阵与平移变换矩阵。

(2)分别求配对后的模型点集M与目标点集S,点云的重心坐标CM、CS;pi经过R矩阵变换后的新的位置为pi′;令ICP所求变换匹配中的平均配对距离为E;ICP迭代的目的是求出R使得E最小。
(6)
(7)
(8)
(9)
(3)由数学推导[17]可知,求旋转变换矩阵R使得E最小,可转换为求旋转变换R使得R×G矩阵的迹最大;其中G=P×QT,P为第i列为pi-CS构造的矩阵,Q为第i列为qi-CT;
P=[p1-CSp2-CS…pN-CS]
(10)
Q=[q1-CMq2-CM…qN-CM]
(11)
G=P×QT
(12)
f(R)=Tr(R×G)
(13)
通过奇异值分解得到G矩阵的U,V,W;
[U,V,W]=svd(G)
(14)
(4)使得f(R)最大的旋转变换R为:
R=W×UT
(15)
(5)平移变换T为:
T=CM-R×CS
(16)
(6)通过上述所计算的旋转变换R以及平移变换T,变换更新目标点集S;
ρi′=R×pi+T
(17)
pi=ρi′
(18)
(7)判断(2)中E是否小于阈值以及迭代次数是否大于设定值,否则重复以上步骤。
3 实验结果与分析
本试验的抓取对象为如图10所示的白色包装瓶。该目标工件的二维图像有着良好的边缘特性。首先进行双目视觉系统中左相机采集图像并进行边缘分割,以便能够区分并标记单个个体。对如图10所示的图像进行边缘处理的结果如图11所示。


经过图像边缘处理后的图像,往往存在如图12所示的边缘断裂现象,对于采用连通域法来进行物体的分割是十分不利的,必须进行有效的边缘修补。


本文采用的方式为:对边缘图像,利用高斯模板进行滤波,对于靠近黑色像素的白色像素会计算一个高斯值,使得白色像素灰度值降低。边缘图像应用高斯模板后,再进行二值化,增大了边缘线的宽度,有效的填补了边缘算子计算时所导致的局部断裂。图13、图14为应用高斯滤波模板以及二值化处理后的局部以及整体边缘图像。由图14可以看出,经过处理后的图像已经能较好分割不同工件二维成像区域。


边缘分割只是将二维图像划分为不同的区域,并不能判定该区域是否为工件二维成像区域。在相机视野中,由于边框、灯光、工件边界交错均会产生局部分割区域。为了减少三维匹配运算量,应尽可能的删除面积过大或者过小的连通域。通过对面积筛选后的连通域进行标记,得到图15所示的图像。
通过图15的单个联通区域的二维图像,标记双目测量中的三维点云,如图16所示。将被标记区部分的点云数据单独取出,进行PCA变换操作。在图17中,PCA变换将任意姿态下的点云数据变换为点云主成分方向与测量坐标系方向一致。将PCA变换后的点云与模型点云进行ICP运算,得到ICP变换矩阵。图18为对单个目标工件进行ICP匹配的结果。通过PCA和ICP的计算步骤,即可得到目标相对于测量坐标系的变换矩阵。以此类推得到其他目标的姿态,将姿态显示在测量点云中,获得图19的结果。




4 结语
如图20所示,通过搭建依靠格雷码结构光和相位移结构光的双目三维测量系统,实现了对散乱堆放工件场景的三维重建。为了能够正确的将散乱件分割、并匹配目标工件的三维位姿,本文利用了散乱堆放工件的边缘特性,首先在二维图像上加以分割,得到目标工件的图像区域,再利用光学几何成像原理,以二维分割图像为基准,对三维点云进行分割。

在计算散乱堆放的目标工件的姿态时,采用了PCA变换与ICP匹配的方式。通过分割后的点云以及模型点云的PCA变换与ICP匹配运算,得到散乱工件堆中可抓取工件集的三维位姿。并应用位姿匹配的结果,控制机器人执行抓取动作,实现散乱堆放工件的分拣工作。图21为通过散乱工件三维视觉检测结果控制六轴机器人进行散乱工件抓取的效果。
