基于LabVIEW的一种柔性机械臂减振控制系统研究

李永超，任 豪，夏瑞强

（1.长安大学工程机械学院，西安 710064；2.长安大学高速公路施工机械陕西省重点实验室，西安 710064）

0 引言

在工业和航空等领域，机械臂应用范围不断扩大，常见的机械臂有刚性和柔性机械臂。柔性机械臂具有灵活性高、结构轻、响应快等优良的特点和性能[1]，但是由于柔性机械臂的弹性变形和残余振动，使得其无法实现精确定位[2]。因此，对于柔性机械臂的研究是机器人研究领域的热门话题。

LabVIEW是一种使用图形化语言的程序开发环境，其程序代码由框图组成。使用图标和连线，可以通过编程对前面板上的对象进行控制。同时Lab⁃VIEW 提供了很多硬件接口，实现不同的仪器仪表功能[3]。本文提出了一种基于LabVIEW 的柔性机械臂减振控制系统，采用欧拉—伯努利梁理论建立了单连杆柔性机械臂的数学模型，采用通过运动参数配置的减振方法来实现振动抑制，并进行了实验研究。

1 柔性机械臂动力学模型建立

本文将电机和机械臂简化为中心刚体和柔性梁，通过Lagrange 方程导出柔性机械臂的动力学模型。在水平面内作回转运动的柔性机械臂系统，如图1 所示，OXY 为固定坐标系，oxy 为固定在柔性臂上的浮动坐标系，根据振动力学[3]得到欧拉—伯努利梁的横向振动微分方程为：

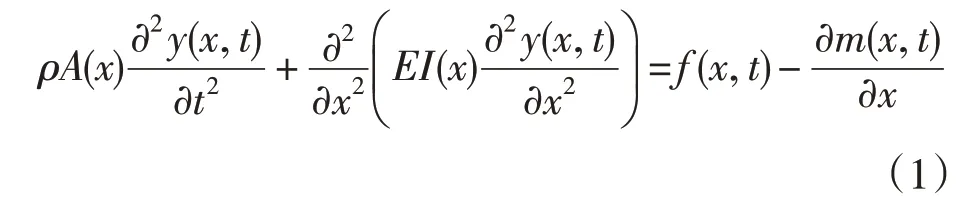
式中：A(x)为横截面积；ρ(x)为线密度；E为弹性模量；I(x)为转动惯量。

根据假设模态法，柔性机械臂是一个分布参数系统，弹性变形y(x,t)可以分解为各阶模态频率ωi对应的振型函数yi(x)与模态坐标函数qi(t)乘积的线性迭加，则柔性臂弹性变形可以近似表示为[4]：

图1 柔性机械臂物理模型

柔性臂上任意一点P变形后的坐标在惯性坐标系OXY中可表示为：

则系统的动能为：

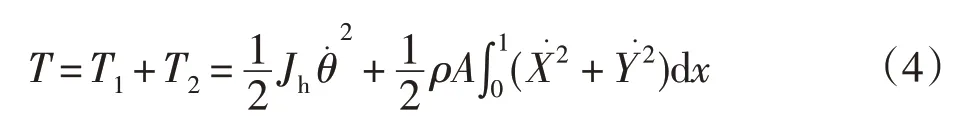
式中：Jh为刚体中心的转动惯量；ρ为柔性臂的密度；A为柔性臂的横截面积。

将柔性臂简化为Euler-Bernoulli 梁，只考虑正应变产生的变形能，则势能为：

选取q=［X Y θ q］，T为系统的广义坐标向量，应用拉格朗日方程：

得到柔性臂系统动力学方程[5-6]：

写成矩阵形式为：

在研究柔性臂振动的时候，将柔性机械臂的终端振动位移y作为系统的输出响应，所以将式（9）转化为状态空间表达式可得：

通过计算可得到柔性机械臂振动的状态空间表达式，进而得到其传递函数[7]：

2 实验模型和平台的搭建

2.1 实验模型参数

本文柔性机械臂实验模型如图2所示，研究对象是一个非均匀截面柔性机械臂，其特点是纵截面为矩形且高度是连续变化的。

图2 单连杆柔性机械臂实验模型

实验平台由4 部分构成，分别为电机、减速器、固定装置和柔性臂。电机带动柔性机械臂做回转运动，电机的输出速度和加速度参数可以通过控制电机的电流来控制，即将运动参数输入机械臂。实验中，研究对象柔性机械臂的材料选用镀锌薄钢板，其各参数统计如表1所示[8]。

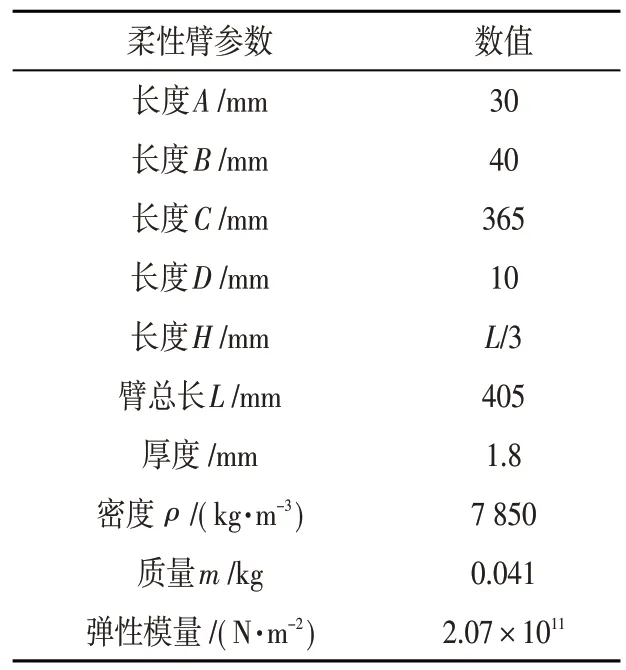
表1 实验模型柔性臂参数统计表

2.2 实验控制系统和平台

本文搭建的柔性机械臂振动控制系统研究实验平台，采用主机上的NI LabVIEW 模块和Compact RIO 测控系统实现[9]。如图3 所示，实验控制系统包括两大部分，第一部分为通过伺服驱动器实现直流电机的实时控制，确定机械臂的运动形式；第二部分为利用应变信号采集器进行控制系统的实时振动测试和数据收集，得到柔性臂振动响应曲线[8]。

本文实验平台中柔性机械臂材料为镀锌薄钢板，所选用的应变片为德国HBM 公司的型号为1-LY13-6/350 系列的应变片。实验中采用半桥连接的应变7 247 组桥方式，在距离固定端x=L/3 处黏贴应变片，实验应变片黏贴如图4所示，在柔性机械臂的两侧对称黏贴各一块应变片，一个受拉一个受压。

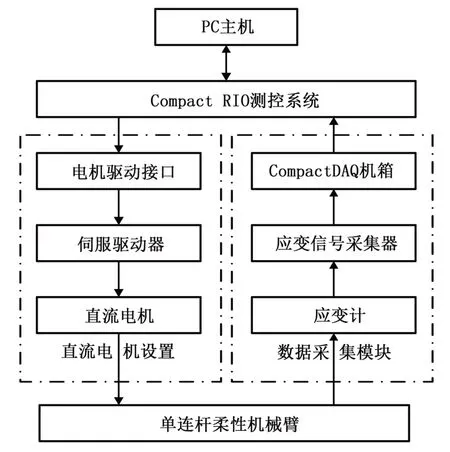
图3 实验控制系统框图

图4 实验应变片黏贴示意图

3 柔性机械臂减振控制思路

3.1 柔性机械臂的参数测定

为了方便研究柔性机械臂的振动现象，首先要获得系统被控对象的振动频率等特性参数，本文在实验测试中采用衰减法获取柔性臂的特性参数。

在自由振动的状态下，敲击镀锌薄钢板收集得到应变片电压信号数据，用Matlab 对数据进行处理得到其衰减振动波形[8]。图5 所示为柔性臂的自由振动曲线，图6所示为柔机械臂响应信号的傅里叶变换。

图5 自由振动响应曲线图

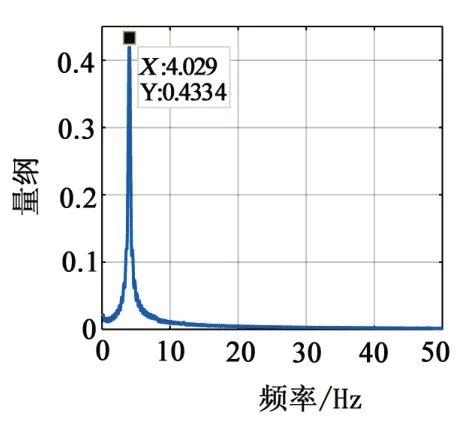
图6 响应信号的FFT变换

根据实验数据可以得到镀锌薄钢板的一阶振动周期T=250 ms=0.25 s，也即一阶固有频率为4 Hz。从图6所对应的傅里叶变换曲线可以看出柔性臂系统的一阶固有频率为4.03 Hz。

3.2 柔性机械臂运动参数配置

根据控制信息的来源可以将减振控制分为前馈控制和反馈控制，其中前馈控制是基于系统输入的一种控制策略，其优点是实现方法简单，可以预先改善系统的性能。在柔性机械臂减振方面，输入整形技术应用十分广泛，原理是在一定时刻施加方向相反、不同幅值的脉冲信号，使得两脉冲响应振幅之和为0。现将柔性臂的运动可分为“加速—匀速—减速”3个运动阶段，柔性臂在加速和减速期间受到电机的冲击而变形发生振动，合理地配制运动时间可以减少运动结束后的残余振动[8-10]。设柔性机械臂运动的角度为θ，角速度为ω，角加速度为α，当柔性臂运动角度确定后，可以根据等式（12）～（13）规划出角速度的梯形曲线。

为了方便计算，设置加减速运动阶段的角加速度数值相等，同时将加减速阶段的运动时间均设置为柔性臂一阶振动周期T。柔性臂运动过程先加速到角速度ω=ω0，然后以最大角速度ω0匀速运动，最后减速到0，所以运动的角度θ即是角速度的积分，可以表示为：

式中：ω0为最大角速度；t1为加减速段的时间，即柔性臂一阶振动周期；变量t为中间匀速段的时间。

4 实验结果与分析

根据运动参数配置的思路，将加速段和减速段设置为角加速度6.28 rad/s2，所以运动最高角速度设置为1.57 rad/s，使得加速段时间约等于柔性臂的一阶振动周期，设置目标运动角度为π/2=1.57 rad，得到如图7所示的角速度曲线、运动角度曲线、振动曲线以及速度—振动的整合曲线。本实验平台通过应变计采集柔性臂弯曲形变的电压信号，通过数据分析电压的幅值得到柔性臂的振动状态，单位mV。

通过图7可以得知，柔性臂在运动过程中的加速和减速段有较大的变形量，主要是因为电机驱动转矩突变；在中间匀速段，柔性臂基本恢复原来状态；在运动结束后，柔性臂残余振动抑制效果明显。

图7 柔性机械臂运动控制速度规划实验曲线

通过采集电压信号得知，机械臂运动过程中末端的最大振幅对应的电压分别为-1.50×10-3mV，机械臂完成加速、匀速和减速三段运动后的1 s 内，末端存在最大的残余振动振幅对应的电压为-1.037×10-4mV，应变电压相对减少了93.27%，其中应变电压的正负值表示振动方向。

实验研究的结果分析表明本文所提减振控制思路的有效性和正确性，合理地利用柔性臂的振动固有周期进行运动参数配制可以大幅减少系统残余振动。

5 结束语

本文针对所提出的通过运动参数配置的减振控制方法，基于LabVIEW和NI板卡搭建柔性机械臂减振控制系统实验平台，并以镀锌薄钢板为研究对象进行了实验研究。

（1）首先建立柔性机械臂的动力学模型，介绍实验平台的结构、镀锌薄钢板模型和参数、控制系统框图和应变片的测量电桥。

（2）通过信息采集系统对研究对象的固有周期和阻尼比进行测定和计算；根据机械臂的振动特点，合理地利用柔性臂的振动周期进行运动参数配制。

（3）进行实验研究，对得到的实验数据进行分析，结果表明当系统的加减速时间等于系统的一阶振动周期时，可以大幅减少系统残余振动，本文的柔性臂减振研究是正确且实用的。