桩- 锚支护在某临水泵站深基坑工程中的应用与分析

2021-03-01高程鹏

城市道桥与防洪 2021年2期

高程鹏

［上海市政工程设计研究总院（集团）有限公司，上海市200092］

0 引言

在现行的临水深基坑工程设计中，常采用的支护形式包括支撑式排桩围护、地下连续墙围护、桩锚式排桩围护等。其中，支撑式排桩围护与地下连续墙围护对于内部结构复杂的大型取水泵站等构筑物，需要进行繁琐的换撑，或将支撑埋入与支撑相交的池壁中再割断支撑，施工过程较为繁琐。而桩锚式排桩围护在土层条件适宜的情况下，可以不设置内支撑，方便施工；且场地标高不要求整平至同一标高，对场地标高起伏较大的基坑工程有很好的适用性[1-2]。

本文以国内西南部某城市取水工程中的泵站深基坑为例，介绍了桩- 锚支护在临水深基坑中的设计应用，并利用Midas GTX NX 软件建立了有限元分析模型。通过模拟基坑分步开挖的施工工况，分析了开挖过程中预应力锚索与围护桩的受力和位移变化及地表沉降的变化规律，并与现行规范中推荐的m 值计算方法和工程实际监测数据进行了对比。

m 值法为现行规范推荐方法[6]，在目前许多基坑设计软件中（如启明星frws、理正深基坑等）均广泛应用，采用了常规的摩尔库伦本构模型（MC 模型）。在实际工程设计中，工程师大多依赖于规范推荐的m 值法进行基坑围护设计。而m 值法的计算结果与各层岩土体的水平反力系数m 值的取值有关，在缺少实地经验与试验的条件下，仅依据规范推荐的经验公式计算得到的水平反力系数m 值，可能会导致计算结果与实际基坑变形产生一定偏差。

因此，本文借助于实际工程案例，对比分析了m值法、有限元法与基坑监测数据，其结果表明，针对本工程案例，m 值法不能真实反映拉锚系统的内力重分布过程；有限元法计算得到的地表沉降与实测沉降数据吻合较好，其桩身变形曲线规律与实测桩身变形数据较接近，但其计算得到的最大桩身位移小于实测数据。在实际工程设计中，可在采用m 值法的基础上辅以有限元分析，以对基坑围护变形有更加准确的判断。

1 工程概况

国内西南部某城市取水工程中，新建单体取水泵站基坑平面尺寸为83.05 m×71.80 m，最大开挖深度17.80 m，基坑安全等级为一级。取水泵站位于某已建干渠工程渠首部位，西侧临近水库（即取水水源），距离水库边仅20 m。因此，基坑开挖前，须在基坑西侧现状渠首部位先施工挡水围堰，并疏干工程范围内的地表水，然后再向下开挖基坑。基坑北侧与南侧为现状民居（距离在50 m 以外），西侧为现状水库，东侧为已建干渠工程中的闸门控制室（单层框架结构）。

泵站基坑平面布置见图1，图1 中的数字表示场地绝对标高。由图1 可知，现状场地标高起伏较大。若将场地标高整平至同一标高，则整平所须开挖（回填）的土方量较大，且对周围建筑及水库环境影响较大。在无法将场地标高整平至同一标高时，内支撑式围护方案适用性较差，而桩锚式排桩围护方案具有施工简单、经济性好、工期短等优点。因此，在经过方案比选后，本基坑采用了桩锚式排桩围护基坑方案。

图1 泵站基坑平面布置图（单位：m）

根据地勘报告，场地地貌属于侵蚀、剥蚀圆状低丘陵地貌。场地土性质自上而下见表1。场地的地表水为水库水，水库的常水位标高为75.5 m。场地的地下水为赋存于砂岩裂隙中的基岩裂隙水，与水库水位有紧密的水力联系，因此水量补给来源丰富，泵站基坑需施工止水帷幕。

2 支护结构设计方案

2.1 围堰

在清除河底淤泥后围堰采用袋装土回填的方式筑成。围堰筑成后再施工基坑围护结构。围堰回填区需行走钻孔灌注桩机的区域采用适当比例的灰土回填。

2.2 围护结构

围护结构采用荤素咬合桩+ 预应力锚索的支护形式。排桩为φ1 000@700 荤素咬合桩，咬合处补设φ100 二次注浆管，兼做基坑止水帷幕。施工时先施工A 桩(素混凝土桩)，后施工B 桩(钢筋混凝土桩)，A 桩与B 桩均采用水下C30 混凝土，A、B 桩长一致。荤素混凝土咬合桩示意见图2。

图2 荤素混凝土咬合桩示意图

预应力锚索为拉力分散型锚索，单根锚索体采用1×7 预应力钢绞线，公称直径15.2 mm，抗拉强度标准值1 860 MPa。锚索成孔倾角(和水平面夹角)采用20°～30°布置，成孔直径为150 mm。拉力分散型锚索结构大样见图3，其中第一段锚固长度与第二段、第三段锚固长度相等。注浆采取二次注浆工艺，注浆材料为水泥浆，水灰比0.5。水泥均采用42.5 级普通硅酸盐水泥，并掺早强剂。锚索的张拉与锁定采用循环单拉单锁法，即在进行锚索张拉时，先张拉并锁定长度最短的锚索组，然后按照由短到长的顺序依次张拉并锁定长度较长的锚索组。在所有锚索完成单次张拉锁定后，再同第一次顺序再进行一次单拉单锁，以此避免张拉锁定过程中的预应力损失。

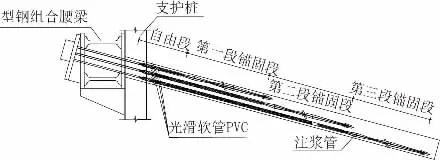
图3 拉力分散型锚索结构大样图

2.3 典型支护剖面

基坑典型支护剖面见图4、图5。

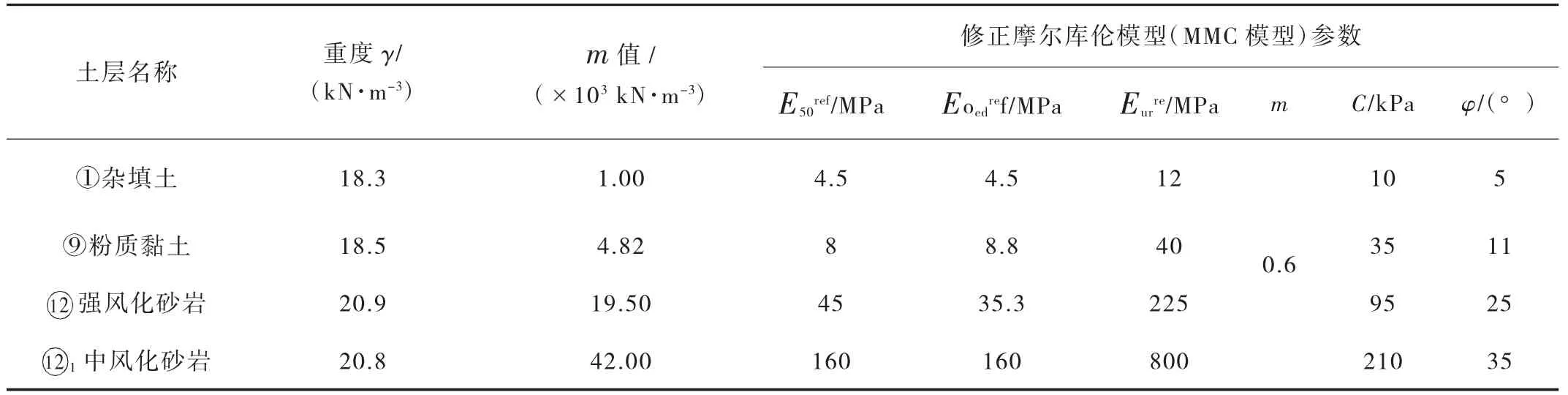
表1 土层分层及土层参

图4 基坑支护1-1 剖面

图5 基坑支护2-2 剖面

图4 所示为基坑围堰侧的剖面示意图。基坑剖面开挖深度13.8 m，基坑顶部5.5 m 范围为挡水围堰。基坑采用两排锚索，第一排锚索水平间距2.4 m，第二排锚索水平间距4.8 m，成孔倾角均为30°，第一排锚索预加拉力值为200 kN，第二排为250 kN。

由图4 可知，水库常水位高度为75.5 m，洪水位高度为80.5 m。如果按照最高洪水位设计围堰，则围堰的堰脚会进入水库航道线，来往船只可能会掏空侵蚀围堰堰脚，对围堰安全反而不利。因此，围堰顶设计标高为77.0 m，而基坑围护结构按照围堰顶标高为81.0 m 的堆土荷载进行设计。若施工过程中水库水位抬高至77.0 m 以上，围堰顶部可以进行临时堆土挡水。

基坑开挖深度最大侧的剖面示意见图5。图5中基坑剖面开挖深度17.8 m，基坑顶部4 m 范围内进行放坡。基坑采用三排锚索，第一排锚索水平间距2.4 m，第二、三排锚索水平间距4.8m，成孔倾角均为20°，各排锚索的预加拉力值均为350 kN。

3 数值计算模型

由于现场场地标高起伏较大，图5 所示的基坑支护剖面开挖深度最深，为本基坑工程中的最不利剖面。因此，本文采用Midas GTX NX 软件对图5 所示基坑支护剖面进行了数值模拟。模型尺寸为93 m×48 m×47.5 m（x×y×z），模型共划分19 895个节点，30 440 个单元，见图6。土体本构采用Midas GTX NX 中的修正摩尔库伦本构模型（MMC 模型），各土层的主要模型参数见表1，参数的取值源自于项目地质勘查报告，也参考了其他文献[3-4]。

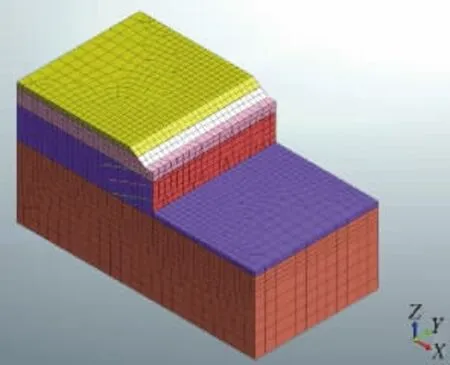
图6 基坑支护有限元模型

锚索采用植入式桁架单元进行模拟。实际工程中拉力分散型锚索张拉与锁定采用的是循环单拉单锁法。在数值模拟中为加快计算速度，假定各排锚索的预应力一次性加载完成。各排锚索的预应力均为350 kN。

基坑围护结构可按照刚度等效原则转化为有限元模型中的板单元进行等效模拟[5]。围护桩尺寸为φ1 000@700 荤素混凝土咬合桩，可用厚度为0.85 m的板单元进行等效模拟。桩锚体系的有限元模型见图7。

图7 桩锚体系有限元模型

基坑开挖遵循“先撑后挖”的原则分步分层开挖，共分为9 个工况，各工况模拟过程见表2。

表2 开挖工况表

4 数值计算结果分析

4.1 锚索轴力变化

图8 所示为有限元法与m 值法下三排锚索的轴力随开挖工况的变化曲线。m 值的取值与土的黏聚力、内摩擦角以及围护桩在坑底处的水平位移量有关，各土层的m 值取值见表1。

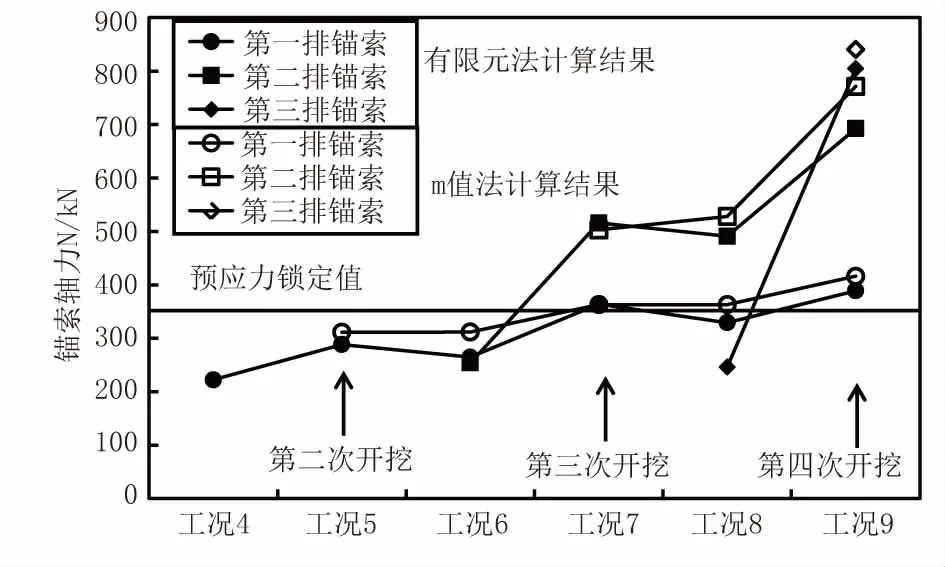
图8 锚索轴力随开挖工况的变化

从图8 中可以看出，在各排锚索张拉锁定后，由于施工过程中的预应力损失，锚索轴力均略小于预应力锁定值350 kN。在有限元法中，第一排锚索张拉完成（工况4）后，向下进行第二次开挖（工况5）时，第一排锚索轴力有所提高；之后再第二排锚索张拉（工况6）后，第一排锚索轴力又有所下降。对于第二排锚索也是如此，在第三排锚索张拉（工况8）时，第二排锚索轴力有所下降。即每次下一排的锚索的张拉都会使整个拉锚系统内力重分布，导致上一排锚索轴力有所下降，这与实际工程经验相符合，在以往研究中也得到过验证[7]，是较为合理的变化趋势。而在m 值法中，受土体本构模型与桩锚模型过于简化，锚索内力随着开挖的进行一直呈增大趋势，没有表现出下一排锚索张拉导致整个拉锚系统内力重分布的变化趋势。

4.2 地表沉降与基坑顶部位移

图9 所示为地表沉降随开挖工况变化的数值模拟结果。从中可以看出，地表沉降在距离基坑围护桩5 m 处达到最大值，最大沉降值为14.1 mm。从第一次开挖到第二次开挖，最大沉降值增量为0.8 mm；从第二次开挖到第三次开挖，最大沉降值增量为2.5 mm；从第三次开挖到第四次开挖，最大沉降值增量为4.8 mm。即随着开挖向下进行，地表沉降增量不断增大。

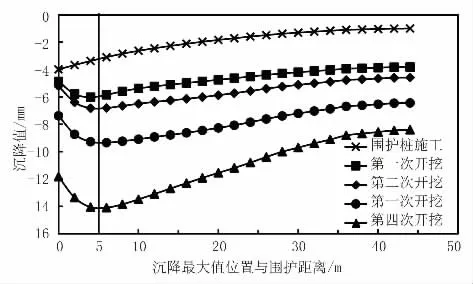
图9 地表沉降随开挖工况变化的有限元数值模拟结果

图10所示为基坑桩顶处及桩后5 m 处的沉降实测数据。从中可以看出，基坑桩顶处最大沉降为5.4 mm，与有限元计算结果有一定差异。桩后5 m 处最大沉降为18.5 mm，且随着基坑向下开挖，地表沉降量也在不断增大，与有限元计算结果吻合较好。即有限元法不能准确反映基坑桩顶处位移的变化，但是能较准确地反映桩后5 m 处的地表沉降发展趋势与最大沉降值。

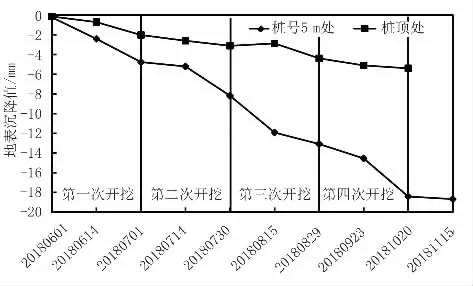
图10 地表沉降变化的实测数据

4.3 围护桩位移

图11所示为有限元法与m 值法下围护桩位移随开挖工况的变化结果对比。

图11 围护桩位移随开挖工况的变化

在有限元法与m 值法计算结果中，随着基坑向下开挖，围护桩位移最大值均不断增大，且位移增量也在不断增大。在第二次开挖完成并施工第一道锚索后，受锚索预应力的影响，围护桩顶均发生朝向基坑外侧的位移。

同时，对比图11（a）与（b）可知，m 值法计算结果中，在基坑开挖到底时桩顶与桩底的位移均接近0；最大位移为22 mm，发生于深度8 m 处。有限元法计算结果中，在基坑开挖到底时桩顶位移为9 mm，桩底位移为5.7 mm，最大位移为14 mm，发生于深度8.2 m 处。m 值法的最大位移为有限元法最大位移的1.57 倍。

图12 所示为基坑围护桩深层水平位移随开挖工况变化的实测数据。实测数据有一定的离散性，在基坑开挖到底时，桩顶与桩底位移均为7.5 mm 左右，最大位移为14～19 mm，最大位移发生于深度-12 m 附近。从中可以看出，m 值法计算得到的桩身最大位移与实测数据较接近，但其桩身变形曲线规律与实测数据相差较远；有限元法计算结构的桩身变形曲线规律与实测数据较接近，但其计算得到的最大位移小于实测数据。