考虑余热回收系统发电的船舶电力系统配置优化研究
2021-03-01高谦,商蕾,管聪
高 谦,商 蕾,管 聪
(武汉理工大学 能源与动力工程学院,湖北 武汉 430063)
电力系统供应船舶正常运营时所需的电能,其提供的能量应能够实时满足船舶的电力负载需求,如果电力系统的容量配置过小,则会对船舶运行时的可靠性及经济性造成消极影响,无法保障船舶的稳定运行;另一方面,如若电力系统的容量配置过大,则会造成能量系统的冗余,大幅度增加系统的初始配置成本,影响船舶的经济性[1]。目前,大多数船舶的电力系统采用的是多台同容量柴油发电机组的配置方案,该方案根据船舶电力负载的高低调整并网发电机组的数量,使发电机组维持较高的运行效率[2]。图1为配备有余热回收系统的船舶电力系统示意图,由于余热回收系统可以回收主机排气中的部分能量并转化为电力输出,现有的配置方案存在低电力负荷时发电机组功率过剩、运行效率较低的问题[3]。因此,本文将基于目标船舶的实际电力负载,考虑余热回收系统的回收电量,对船舶电力系统的配置优化方法展开研究。

图1 配备有余热回收系统的船舶电力系统示意图
1 余热回收系统仿真分析
余热回收系统的发电量随船舶主机负荷的变化而变化,建立余热回收系统仿真模型可帮助分析系统的工作特性。本文以某4 500 TEU集装箱船为研究对象,其配备的主机为MANB&W公司的7K98MC型二冲程废气涡轮增压式低速柴油机,额定转速为94 r/min,额定输出功率为40 055 kW,目标船余热回收系统示意图如图2所示。

图2 目标船余热回收系统示意图
余热回收系统由余热锅炉和汽轮发电机组成,余热锅炉又包括经济器、蒸发器及过热器3个部分。余热回收系统内包含有3套循环,分别是图2中点线所示的经济器循环,点划线所示的蒸发器循环以及虚线所示的过热器循环。其循环过程为:来自热井的锅炉给水经给水泵增压后,进入预热器中,同增压经济器循环水换热后流入汽包内,由循环水泵增压的蒸发器循环水在锅炉蒸发器中,同主机排气换热后部分变为饱和蒸汽并回到汽包中,随后饱和蒸汽从饱和水中分离,分离后的蒸汽一部分被供给蒸汽加热设备使用,另一部分饱和蒸汽则进入锅炉过热器中与主机排气换热变为过热蒸汽,过热蒸汽随后进入汽轮发电机中膨胀做功,汽轮发电机发电,之后蒸汽经冷凝器中的海水冷却,再经凝水泵增压后流回热井中,完成整个汽水循环过程。
1.1 余热回收系统数学模型
余热锅炉正常运行时,依据质量守恒定律可知,从热井中进入汽包的饱和水的质量应与从汽包中流出的饱和蒸汽的质量相等,而汽包内饱和蒸汽的唯一来源是蒸发器,故从汽包中流出的饱和蒸汽的质量也应与由蒸发器产生的蒸汽的质量相等,由此可得:
qmw=qms=qmse+qmss,
(1)
式中,qmw为热井给水的质量流量,qms为饱和蒸汽的质量流量,qmse为供给加热设备的蒸汽的质量流量,qmss为流向过热器的蒸汽的质量流量,单位均为kg/s。
流向过热器的蒸汽在过热器中吸热变为过热蒸汽,随后进入汽轮发电机中驱动汽轮发电机发电,将过热蒸汽在汽轮发电机中的膨胀过程假设为等熵过程,由此可得汽轮发电机的发电量pelec为:
pelec=qmss(hSTi-hSTo)ηSTGfbfTfL,
(2)
式中,hSTi、hSTo分别为汽轮机进、出口的蒸汽焓值,kJ/kg;ηSTG为汽轮机效率;fb、fT、fL分别为汽轮机背压、气体温度以及负载修正系数。
1.2 余热回收系统仿真模型
在MATLAB/Simulink环境中搭建的柴油机余热回收系统仿真模型如图3所示。仿真模型的输入为柴油机的设定转速Nord,PID调速器接收设定转速及柴油机本体反馈的实际转速Neng与扫气箱压力Pscav后,计算并输出柴油机油门位置FR,之后柴油机本体及余热回收系统经运算输出主机的排气温度TWHRS、质量流量qmWHRS,以及余热回收系统发电量Pelec等参数。
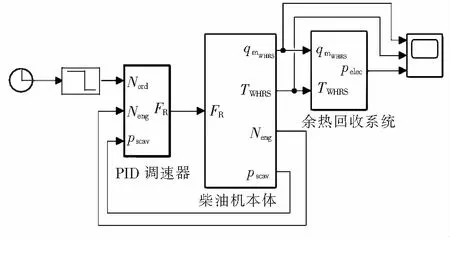
图3 柴油机余热回收系统仿真模型
将柴油机转速依次设定为74.61 r/min、85.40 r/min、89.04 r/min及94.00 r/min,分别对应的柴油机负荷为50%MCR、75%MCR、85%MCR及100%MCR(MCR为柴油机的最大输出功率),运行仿真模型,得到的仿真结果如图4所示。由图4可以看出,随着柴油机负荷的增大,系统回收电能也在增大,其中,柴油机负荷由85%MCR升高至100%MCR的过程中,增大趋势较为明显,由1 567 kW上升至2 397 kW,其原因是柴油机负荷为100%MCR时的废气温度要显著高于负荷为85%MCR时的废气温度。而经旁通后,柴油机负荷为50%MCR时的废气温度虽然近似等于负荷为100%MCR时的废气温度,但因50%MCR下的废气质量流量较小,故电能回收也较少。
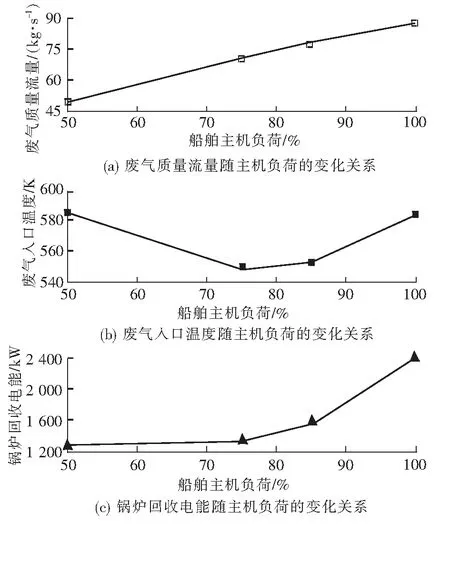
图4 余热回收系统模型仿真结果
2 电力系统容量配置优化数学模型
船舶不同状态下电力系统的负载大小不尽相同,本文目标船在香港—新加坡航线用作班轮运输,其整个生命周期可视作由在香港—新加坡航线上往返的各个航次组成。一个航次可分为在港装货、航行以及到港卸货3个阶段,假定装货时船舶的电力负载为A,停泊时长为tA;卸货时船舶的电力负载为B,停泊时长为tB;航行时船舶的电力负载为C,航行总时长为tC。由文献[4]可知,船舶航行时主机功率随时间t变化,因此可认为C是随时间t变化的函数C(t),C(t)min是航行时最小电子负载函数。对于目标船,这3种负载之间存在以下关系:
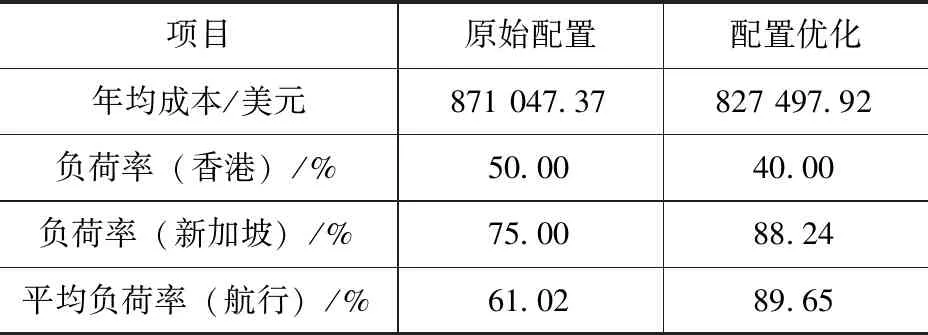
A (3) 由余热回收系统的仿真分析可知,系统发电量同样与主机负荷有关。因此,汽轮发电机的实际输出功率亦可看作是关于时间t的函数PSTG(t)。根据目标船的电力负载状况,即可以确定目标船的电力系统配置方案,目标船电力系统配置方案如表1所示。 表1 目标船电力系统配置方案 该方案采取设立1台功率较小的辅助柴油发电机组的做法,即配备1台容量为PDG1的辅助柴油发电机组,应小于A。船舶装货阶段由1台容量为PDG2的柴油发电机组单独在网运行,卸货阶段则由辅助柴油发电机组与其并网运行。航行阶段的船舶则由辅助柴油发电机组与汽轮发电机并网运行。 船舶电力系统容量配置优化的目的是提高系统设备的运行效率,提升船舶的经济性,因此,本文综合选取了电力系统初始布置成本Cc、运行成本Cf以及维护成本Cm作为优化目标,可表示如下[5]: Cc=cc·(PDGn/Pref)ic·PDGn, (4) (5) (6) 式中,cc=788.4美元/千瓦、ic= -0.6、Pref=1 000 kW,均为柴油发电机组初始布置成本的拟合系数;cf= 419.85美元/吨,为燃油平均价格;cm= 0.006 891 美元/千瓦时,为柴油发电机组维护成本拟合系数;PDGn、PDG分别为柴油发电机组的额定输出功率与实际输出功率,kW;ge为柴油发电机组的燃油消耗率[5],g/(kW·h)。 作为优化目标函数的系统年均成本CY,可表示为: CY=Nt·(Cf+Cm)+Cc/Y, (7) 式中,Nt=τ/(tA+tB+tC),为目标船一年的总航次数,τ= 8 760 h;Y为目标船工程周期年限,其值为20[4]。 为应对可能的突发状况,船舶电力系统至少需要留有10%的功率裕量,以保证船舶供电的安全性[6],据此给出的优化约束条件为: TA≥0.1,TB≥0.1,TC(t)≥0.1, (8) 式中,TA、TB及TC(t)为目标船处于装货、卸货及航行阶段的功率裕量,是船舶电力系统提供高于额定输出功率的后备能力,以百分比表示。 综合上述目标函数及约束条件,可得到船舶电力系统配置方案的优化数学模型为: minCY, (9) 目标船在香港—新加坡航线用作班轮运输,航线与船期要求相对固定,本文将采用目标船以恒定航速航行的一个航次作为优化算例。该航次中,目标船首先在香港停泊装载货物,电力负载为1 000 kW,耗时9 h;之后以恒定航速20 kn航向新加坡,航行耗时72 h,航行阶段主机每小时的平均功率为PDE,目标船主机每小时平均功率如图5所示,航行阶段的电力负载Pload=-3 451+540lnPDE[7],目标船抵达新加坡后靠港卸载货物,卸载耗时9 h,电力负载3 000 kW。 图5 目标船主机每小时平均功率 采用自适应权重粒子群算法对优化模型进行求解,设定算法的粒子数目为100;搜索空间维度为2,分别对应2台柴油发电机组的容量PDG1及PDG2;迭代次数取50次;惯性权重系数最大值为1.0,最小值为0.1。将算例信息代入配置优化数学模型中,配置优化模型求解流程如图6所示。 图6 配置优化模型求解流程 配置优化模型寻优关系如图7所示。由图7可知,算法在迭代21次后寻得最优解,之后保持不变,迭代得到的最优年均成本为827 161.4美元,该年均成本对应的算法求解结果为PDG1= 909.86 kW,PDG2=2 423.47kW,综合考虑目前市售柴油发电机组标准容量后,其修正结果为PDG1= 900 kW,PDG2=2 500 kW。 本文目标船的原始配置为2台2 000 kW的柴油发电机组,原始配置与配置优化的对比见表2。 对比表2中数据可知,配置优化方案相较原始配置方案年均节约成本43 549.45美元,成本减少约4.99%;同时,综合来看,采用配置优化方案时,柴油发电机组的负荷率也要高于采用原始配置方案时发电机组的负荷率,这验证了本文优化方法的正确性与有效性。 采用配置优化方案时,目标船航次内电力系统中各设备的功率输出如图8所示。由图8可知,目标船在香港停泊时,电力负载由2#发电机组承担,输出功率为1 000 kW;目标船在新加坡停泊时,电力负载由2台发电机组按等负荷率共同承担,1#发电机组输出功率为794.16 kW,2#发电机组输出功率为2 205.84 kW;船舶航行阶段,1#发电机组与汽轮发电机并网运行,承担电力负载超出汽轮发电机输出功率的部分,约占整体电力负载的30%,1#发电机组的负荷率基本维持在70%~80%之间。 图7 配置优化模型寻优关系 表2 原始配置与配置优化的对比 图8 目标船航次内电力系统中各设备的功率输出 本文基于目标船的实际电力负载,考虑余热回收系统的回收电量,建立了目标船余热回收系统的仿真模型以及船舶电力系统配置优化的数学模型,并采用自适应权重粒子群算法对优化数学模型进行了迭代求解;计算所得的配置优化方案相较原始配置方案,年均节约成本43 549.45美元,成本减少约4.99%,同时综合来看,采用配置优化方案时,柴油发电机组的负荷率也要高于采用原始配置方案时发电机组的负荷率;对比分析说明,本文提出的电力系统配置优化方法可以有效降低电力系统的年均成本,提高系统内设备的运行效率。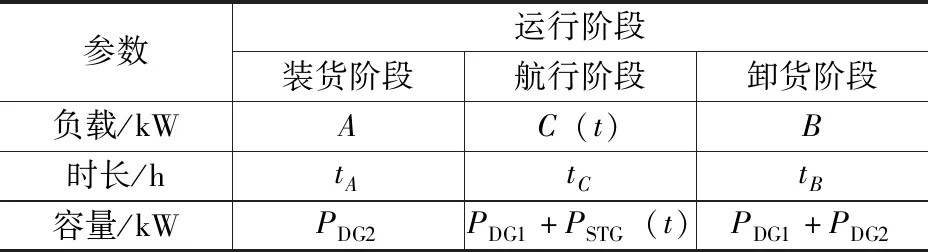
2.1 容量配置优化目标函数


2.2 容量配置优化约束条件
3 模型求解及结果分析
3.1 算例信息
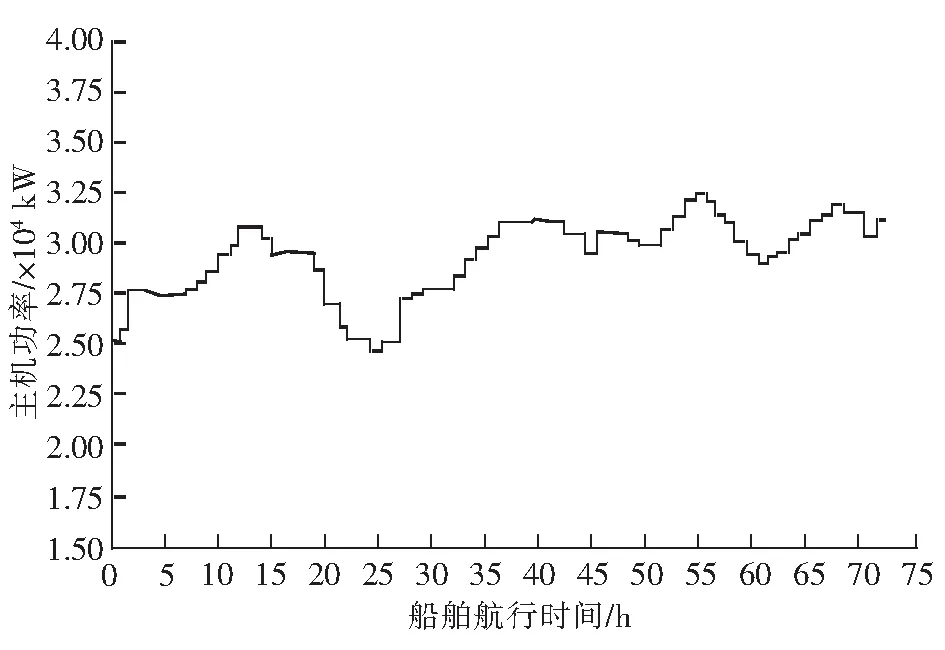
3.2 粒子群算法求解

3.3 结果验证及分析


4 结束语
