管道内检测的环形相控阵超声聚焦方法
2021-03-01杨理践李光辉高松巍王国庆
杨理践,李光辉,高松巍,王国庆,张 佳
(沈阳工业大学 信息科学与工程学院,沈阳 110870)
油气管道是石油和天然气的主要运输工具之一,由于多种原因会导致其产生腐蚀、裂纹等缺陷,严重影响其安全运行。在管道检测的众多无损检测方法中,相控阵超声检测因检测速度快、无辐射、精度高等特性受到诸多关注。
通过相控阵不同阵元产生的声场叠加,由延时法则可实现声束的偏转和聚焦[1-2]。郭忠存等[3]将延时算法应用于圆台形换能器的声场聚焦,分析了圆台形阵列在管材内的辐射位移场特性,实现了圆台形换能器在管材外对管材的聚焦检测;CHOE等[4-5]利用延时特性设计了外半径为1.27 mm,阵元总数为64的环形换能器阵列,分析了基于图形处理单元的图像重建过程。
文章基于相控阵延时法则,分析了管道中环形相控阵超声聚焦声束的传播原理,构建了聚焦数学模型,计算了奇、偶数阵列的延迟时间,验证了管道中环形相控阵超声的检测效果,得到阵元数量与回波幅值的关系。
1 环形相控阵超声检测原理
一维线阵相控阵超声换能器不适合曲率较大的管道内检测,应采用适合管道内检测的环形相控阵超声换能器。
1.1 环形相控阵超声阵列
环形相控阵超声阵列模型及扫描方式如图1所示。

图1 环形相控阵超声阵列模型及扫描方式示意
在图1(a)中,阵列包括矩形压电晶片结构的128个阵元,针对某一聚焦点,最大工作阵元数量为32个,n(1≤n≤32)个阵元按一定的延时法则发射声束,nR(nR≤n)个阵元按一定延时法则接收声束后合成,并在某一阵元的显示界面显示结果。图1(b)所示为阵列扫描方式,若工作阵元数量为n,则第①组按顺时针由第1个阵元开始工作,至第n个阵元结束工作;第②组由第2个阵元开始工作,至第n+1个阵元结束工作,依次按此模式,直至所有阵元依次工作,接收并合成回波信号。若n为奇数,显示合成回波信号的阵元为中间阵元;若n为偶数,显示合成回波信号的阵元为中间两个阵元中阵元号较小的一个。
环形相控阵超声以弧线形顺时针旋转扫描的方式进行管道内检测,得到管道的周向检测信息。在换能器沿管道轴向前进的过程中,即可实现管道的全覆盖检测。
1.2 环形相控阵超声检测方式
管道中环形相控阵超声检测方法如图2所示。

图2 管道环形相控阵超声检测示意
环形相控阵超声进行管道内检测的检测方式包括2种。一种是无聚焦检测方式(见图2),即阵列不施加延时法则,所有阵元激励一次后完成管道一周的检测,此时换能器阵列声束会按一定的分散状态向管道中辐射超声波;另一种是聚焦检测方式,该方式需要确定聚焦的工作阵元数量和焦距,针对声束扫描过程中的某一聚焦点,使同等数量阵元辐射的超声波形成聚焦区域。根据波的干涉原理,由所需阵元数量与焦点位置确定延时法则,在预设焦点位置形成聚焦区域,焦点处超声波能量得到增强,阵元接收到回波信号后对其进行逆向聚焦,获得焦点处的检测信息[6],多阵元信号叠加时,结果显示在距离焦点最近的阵元上。采用如图1(b)所示的扫描方式时,聚焦点紧密排列于管道一周,完成管道一周的检测。该检测方式使检测区域的超声波能量增强,检测效果优于无聚焦检测方式的。
2 环形相控阵超声聚焦延时法则
2.1 管道中声束的传播原理
超声波纵波以一定的角度由耦合剂倾斜入射至管道内壁,产生反射纵波,且由于波形转换,产生折射纵波与折射横波,该过程由折射定律表示为
c1sinθ2=c2sinθ1
(1)
式中:c1为耦合剂中的纵波声速;θ1为入射角;c2为管壁中(折射后)的纵波声速;θ2为折射角。
管道中环形相控阵聚焦声束时,根据焦距F0,换能器半径r,管壁内半径R内和外半径R外关系,存在如下3种聚焦情况:
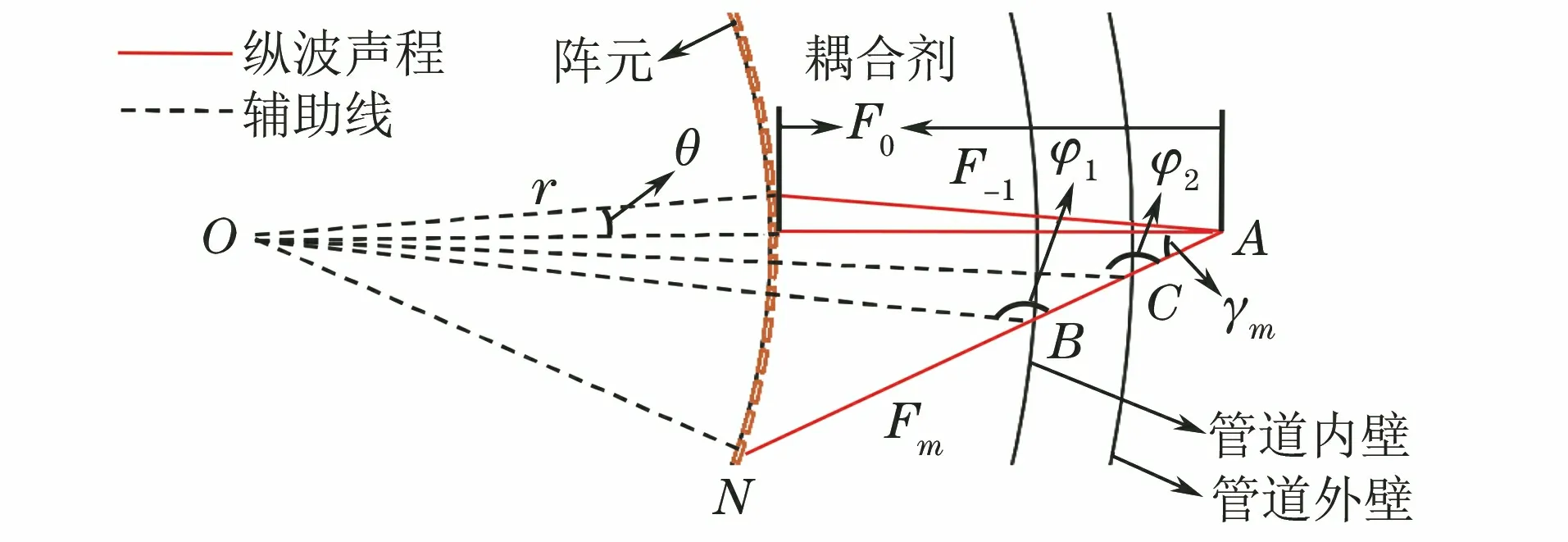
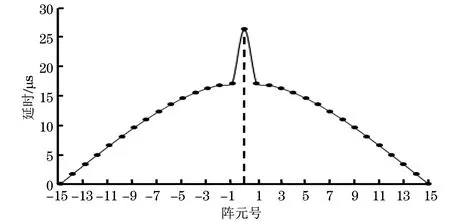
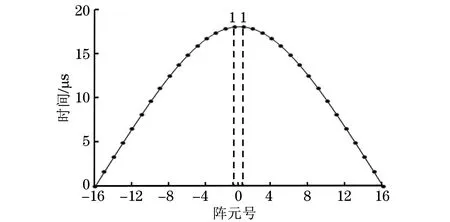
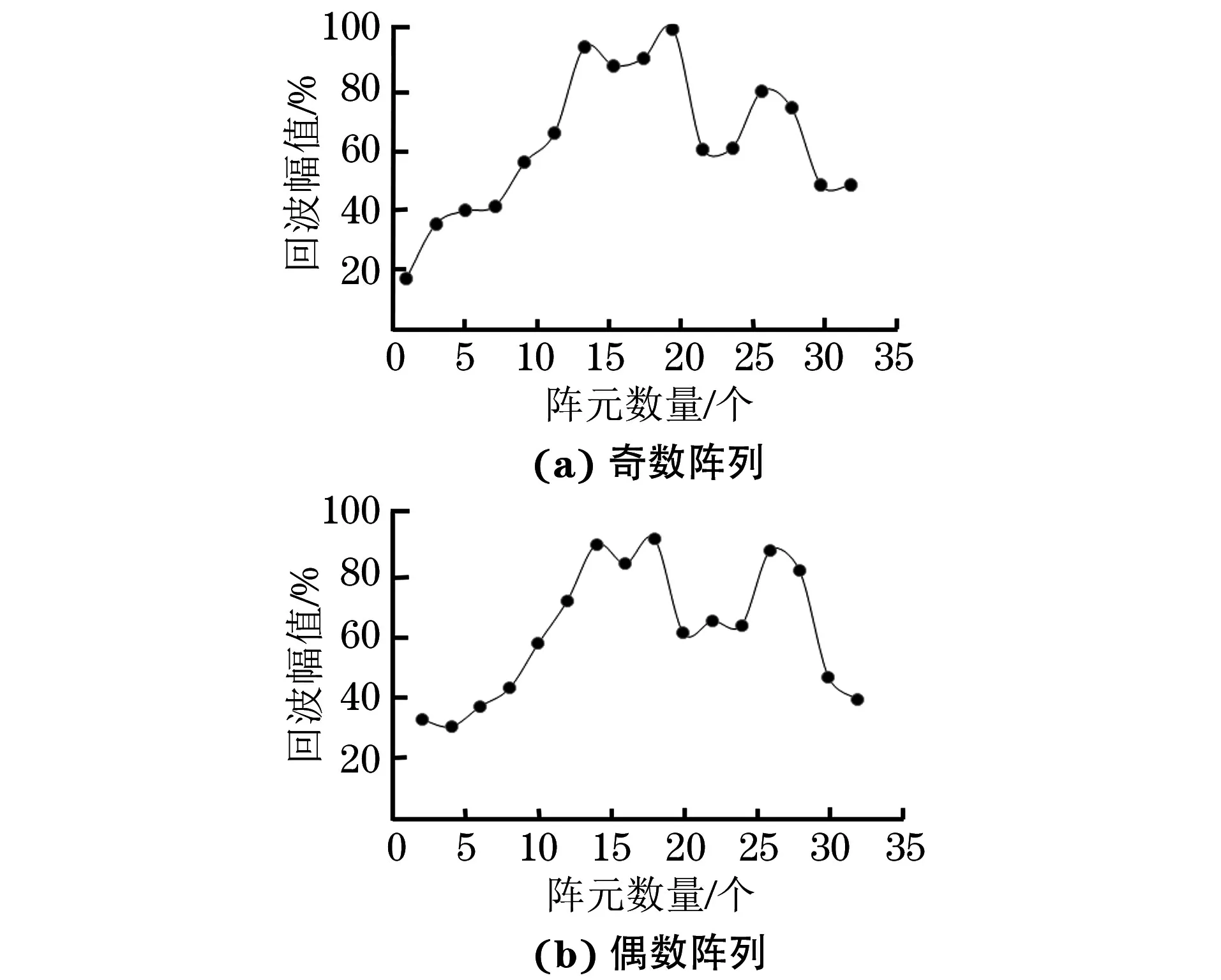
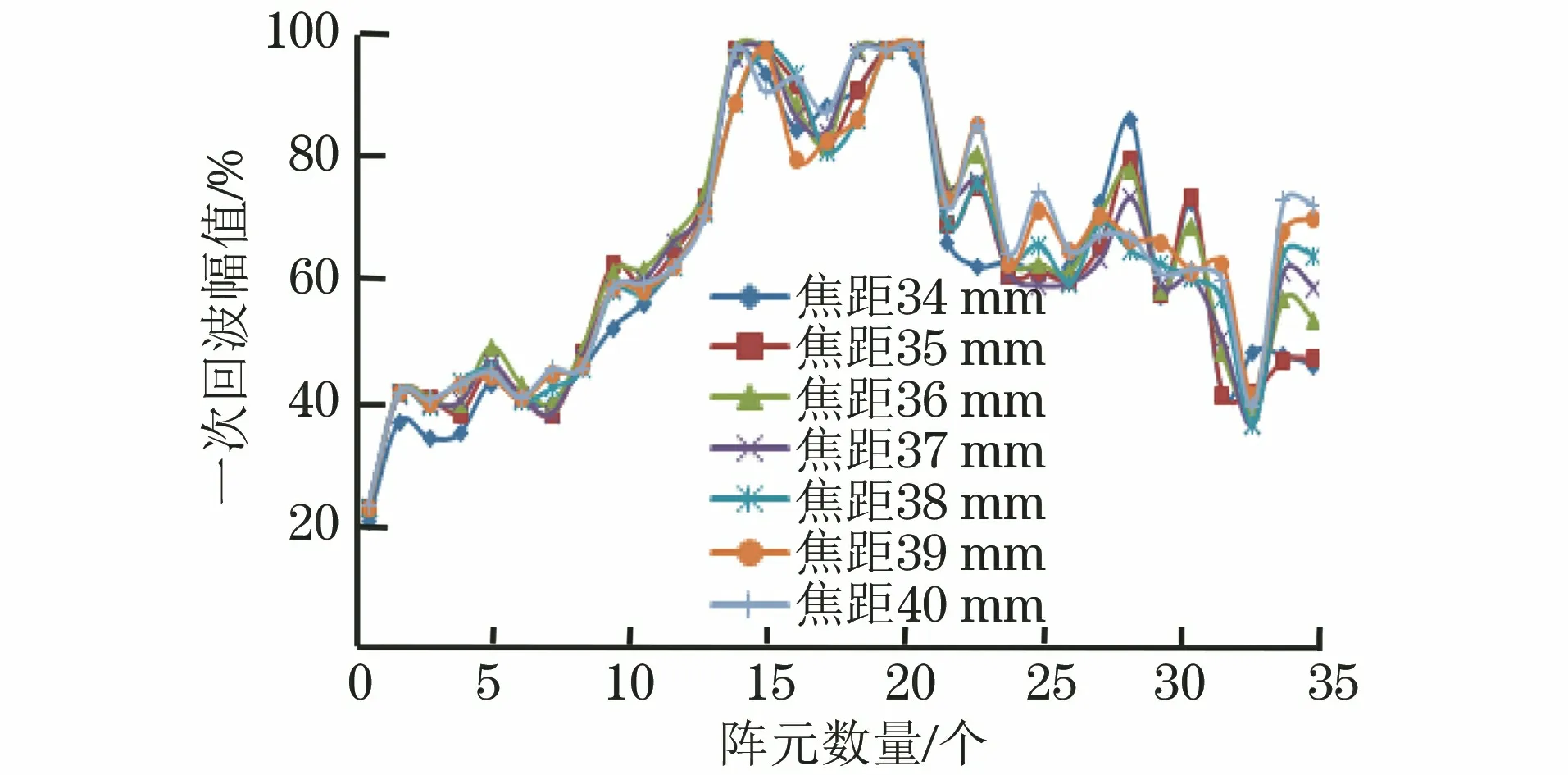
(1) 0 (2)R内-r≤F0 (3)F0≥R外-r,此时聚焦点位于管道外壁以外,声束传播方式如图3所示。由图3可知,预设聚焦点A位于管道外部,焦距大于管道外半径与换能器半径之差,聚焦区域在点A的前方位置,此时的检测方式最佳。 图3 聚焦点位于管道外壁以外时的声束传播示意 相比于超声横波,超声纵波在介质中的声速较快,上位机先接收超声纵波的回波信号,显示其检测结果。为避免其他超声回波信号的干扰,环形相控阵超声管道内检测的超声波类型选择为纵波。 环形相控阵超声阵元尺寸较小,声场覆盖范围较大,根据超声波的叠加和干涉原理,管道内超声波的能量得到增强。在环形相控阵超声聚焦延时法则的计算过程中,需确定阵元中心与聚焦点之间的距离。 2.2.1 奇数阵列聚焦延时法则 环形相控阵超声在管道内检测的声束扫描过程中,设置聚焦所需工作阵元数量为奇数,预设聚焦点A位于管壁以外时,即为奇数阵列聚焦检测方式,其聚焦数学模型如图4所示。 图4 管道内检测奇数阵列聚焦数学模型 在图4中,工作阵元数量为2m+1(0≤m≤15),阵元号以OA为对称轴,中间阵元号为0,第0号阵元上方由近及远为-1-m号,下方由近及远为1m号,聚焦声束成对称分布,相邻阵元圆心角θ为2.812 5°。在ΔONA中,根据余弦定理可知 (2) 式中:点O为环形相控阵超声换能器圆心;点N为第m号阵元的中心;点A为聚焦焦点;Fm为第m号阵元与焦点A之间的最短距离。 由正弦定理可得 (3) 在ΔOBA中,γm为NA与OA之间的夹角,可计算 (4) 式中:φ1为第m号阵元发射声束与内壁交点B的法线与BA连线之间的夹角。 可计算 (5) 在ΔOCA中,可计算 (6) (7) 点B与点C之间的距离为 (8) (9) 式(9)表示第m号阵元与第0号阵元之间的延时。环形相控阵超声奇数阵列聚焦检测时,最大工作阵元数量为31,阵元号与延时的关系曲线如图5所示。奇数阵列的中间阵元为第0号阵元,阵元间延时以第0号阵元为对称轴,呈对称分布。 图5 31阵列阵元号与延时关系曲线 中间第0号阵元与相邻第-1号和第1号两阵元相比,延时之差较大,由于第0号阵元与第-1号和第1号阵元中心到聚焦点之间的距离比其他各个阵元到聚焦点的距离大,故第0号阵元的延时较大,其他各个阵元的延时相对较小。 2.2.2 偶数阵列聚焦延时法则 若设置聚焦所需工作阵元数量为偶数,预设聚焦点A在管壁以外时,则为偶数阵列聚焦检测方式,工作阵元数量为2m(1≤m≤16),其聚焦数学模型如图6所示。 图6 管道内检测偶数阵列聚焦数学模型 在图6中,工作阵元中间两阵元的中点到聚焦点A的距离为焦距F0,工作阵元号以F0所在直线为对称轴,对称轴上方由近及远为-1-m号阵元,对称轴下方由近及远为1m号阵元,第m号阵元中心线与焦距所在直线夹角∠AON′为(m-1/2)θ,以相同的计算步骤对各个阵元中心到聚焦点的距离及相关角度进行计算可得 Fm={r2+(r+F0)2- 2r(r+F0)cos[(|m|-1/2)]θ}1/2 (10) (11) (12) 根据对称性,第-1-m号阵元延时与第1m号阵元延时相同。 为保证阵元中心到聚焦点的距离最短,选择由第1号阵元显示结果。式(12)表示环形相控阵超声偶数阵列聚焦检测时第m号阵元与第1号阵元之间的延时。 偶数阵列聚焦检测时,最大工作阵元数量为32,阵元号与延时的关系曲线如图7所示。在图7中,偶数阵列的中间两个阵元为第-1号阵元和第1号阵元,各个阵元的延时以第-1号阵元和第1号阵元连线的中垂线为对称轴,呈对称分布。 图7 32阵列阵元号与延时关系曲线 偶数阵列与奇数阵列延时法则的区别在于,偶数阵列中间两个阵元延时相同,且中间两个阵元中心到聚焦点的距离与其相邻阵元中心到聚焦点的距离相比,差距较小,中间两阵元与其相邻两阵元在延时上的差异没有奇数阵列明显。 增加工作阵元数量会增加聚焦效果,但环形相控阵换能器阵列表面为凸曲面,工作阵元数量超过某范围后,边缘阵元受偏转能力限制,辐射声场不能覆盖聚焦点位置,合成回波信号有较大误差,所以应将工作阵元数量控制在一定范围内。 设计相控阵超声在线检测试验系统进行管道检测,采用CTS-PA22S/P A16小型相控阵模块,128阵元环形相控阵超声换能器和上位机。被测管道尺寸为148 mm×168 mm×9 mm(长×外径×壁厚),发射与接收超声波的换能器直径为100 mm,厚度为31 mm,晶片长为10 mm,宽为2.45 mm。 环形相控阵超声奇数阵列聚焦和偶数阵列聚焦管道检测试验装置外观如图8所示。在图8中,相控阵换能器中心与管道中心重合,换能器激励电信号与接收回波信号的处理由相控阵模块完成,由上位机得到检测结果。 图8 环形相控阵超声检测试验装置外观 设定管道外壁无缺陷区域为被检区域,检测位置不变,令工作阵元数量从1逐渐增加到32,验证奇数阵列延时法则和偶数阵列延时法则的可行性。 工作阵元数量为奇数时,由距被检测点最近的阵元显示结果。增加工作阵元数量时,以接收合成回波信号的阵元为中心,阵元数向两侧递增;工作阵元数量为偶数时,由距被检测点最近且阵元号较小的阵元显示结果,增加工作阵元数量时,接收合成回波信号的阵元保持不变,以中间两阵元中心线为对称轴,逐渐向两侧递增。 设置数字增益为0 dB,模拟增益为19 dB,焦距为34 mm(聚焦点位于管壁外侧),选择水作为耦合剂,水中的声速为1 480 m·s-1,管道中的声速为5 900 m·s-1。 3.2.1 工作阵元数量 应用环形相控阵超声对管道实施聚焦检测时,需预先确定工作阵元的数量。试验通过调整工作阵元的数量,确定其与聚焦效果的关系。 保持其他参数不变,工作阵元数量由1逐渐增加到32,应用奇数阵列和偶数阵列延时法则,奇数和偶数阵列阵元数量与归一化一次回波幅值的关系曲线如图9所示。 图9 阵元数量与归一化一次回波幅值关系曲线 由图9(a)可见,工作阵元数量为1时,为无聚焦检测方式,回波幅值为17.6%;工作阵元数量大于1时,为聚焦检测方式,回波幅值明显增高。由图9(b)可见,最小回波幅值对应的工作阵元数量为4,幅值为最大值的33.2%,各回波幅值均明显高于无聚焦检测方式的回波幅值。试验中,A扫描结果的最大壁厚为9.7 mm,最小壁厚为8.3 mm,检测误差为-7.78%7.78%。一次回波幅值与回波能量存在正相关关系,回波能量强,即聚焦效果较好,说明奇数与偶数阵列的延时法则实现了环形相控阵超声的聚焦。 工作阵元数量增加至一定值后,回波幅值呈现不规则减弱的趋势,回波幅值高度在最大值50%以上的工作阵元数量为928或30;工作阵元数量为30时,回波幅值为50.8%,幅值有下降趋势,且工作阵元数量增多,检测速度降低,所以选择工作阵元数量为928较好。 由此可见,并非工作阵元数量越多聚焦效果越好,只有选取适当的工作阵元数量,才可得到较好的聚焦效果。 3.2.2 聚焦焦距 焦距与归一化一次回波幅值的关系曲线如图10所示。 图10 焦距与归一化一次回波幅值的关系曲线 在管壁上同一位置,保持其他条件不变,令焦距由34 mm逐渐增加到40 mm,步进为1 mm,工作阵元数量由1逐渐增加到32,接收阵元保持为0号阵元,对φ168 mm的管道进行聚焦检测。由图10可见,焦点在管壁以外时,焦距的变化对环形相控阵超声奇数阵列与偶数阵列聚焦检测的影响较小。 研究了管道中环形相控阵辐射超声波的特性,分析了奇、偶阵元数量的聚焦数学模型,推导了延时法则计算公式,结果表明,在奇数阵列工作模式与偶数阵列工作模式中,工作阵元数量与一次回波信号幅值变化趋势近似,信号幅值先增大后减小;一定数量阵元组合可获得良好的聚焦效果;焦点在管壁外侧时,焦距逐渐增大,对一次回波信号影响较小,具有较好的稳定性。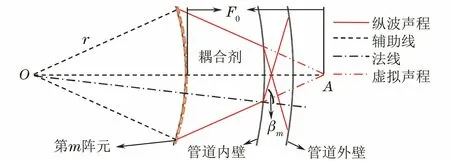
2.2 环形相控阵超声延时法则的计算
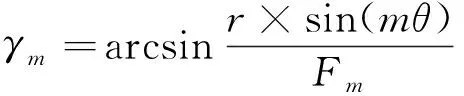


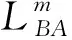
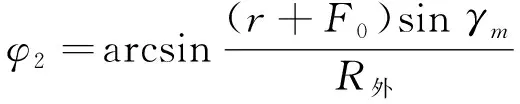
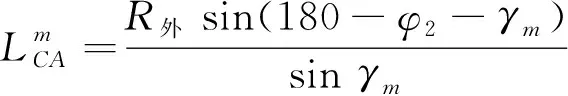

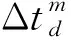
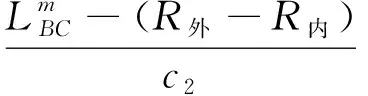


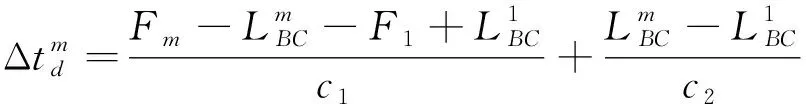
3 试验方法与结果分析
3.1 试验平台

3.2 管道聚焦检测试验
4 结语
