不同体型调压室的瞬态水力特性对比分析
2021-03-01何相慧杨建东杨桀彬胡金弘郑贵桥向正林
何相慧,杨建东,杨桀彬,胡金弘,郑贵桥,向正林
(1.武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2.南方电网调峰调频发电有限公司,广东 广州 510630)
1 研究背景
设置调压室是改善长输水管道水电站运行条件的可靠措施,既可以减少管道的水锤压力,又可以防止由于尾管真空度过高引起的水柱分离,从而提高水电站的运行安全性[1-2]。地形因素对调压室施工有制约作用,影响了调压室的形状和调压室断面积,如何在满足水电站安全运行的前提下,合理设计调压室体型,是每个水电站设计中关键技术问题之一[3-4]。
在数值模拟方面,赵志高等[5]建立了基于电路等效理论的有压管道系统数值仿真模型,有效协调了仿真精度与计算效率之间的矛盾。Harlow等[6]提出的特征线方法(MOC)被广泛用于有压管道系统的瞬态特性研究中,用于求解偏微分方程组[7-11]。陈玲等[9]对比了解析法、数值积分法和特征线法在求解调压室涌浪过程中的区别,结果显示特征线法考虑了水电站管路布置特性,理论精度较高,适用于大中型水电站。Yang等[10-11]将水轮机特性曲线方程改写为空间曲面方程,并提出了基于转速偏差函数机组边界条件的寻根方法。尽管MOC方法可得到调压室水位的数值解,但无法得到调压室水位波动过程中内部流态,该流态较为复杂多变,若产生旋涡、脱流、进气等有害现象,会影响水电站的安全稳定运行。于是,近年来国内外许多学者采用CFD方法对调压室水位波动过程及瞬变水力特性进行了研究。CAI F等[12]通过试验和CFD数值模拟研究了立轴旋涡的产生原因和优化方法,结果表明淹没水深是影响立轴旋涡产生的主要因素,通过减小弗劳德数Fr和速度环量可有效抑制立轴旋涡的产生;邓淞苡等[13]探讨了长廊式调压室不利流态的产生原因,并提出通过增加“消涡墩”的方式消除立轴旋涡;华富刚[14]讨论了长上室调压室的水面瞬态波动,发现CFD 计算值和测试值吻合良好,并通过特征线法与CFD方法结合进行了水电站过渡过程计算。刘飞等[15]探讨了不同湍流模型和边界条件对计算结果准确性的影响,结果表明RNGk-ε湍流模型和Realizablek-ε湍流模型对强旋流的适应性较好,预测精度能够满足工程要求。另外,多位学者的研究表明,CFD计算结果与试验结果具有良好的吻合性,采用CFD 方法进行调压室瞬变水力特性模拟具有良好的精度,可为工程实践提供参考[16-19]。
一维特征线法计算调压室涌浪水位已经得到了广泛的应用和证实,成功地应用于国内外多座水电站的设计中,随着CFD技术的发展和计算机运算能力的提升,利用CFD计算调压室涌浪及局部流态的准确性也得到了验证,但是很少有论文对一维与三维的计算结果进行对比,本文所研究的调压室体型也鲜有报道。因此,基于以上研究成果,本文采用一维数值仿真和三维CFD 对某水电站T型调压室和π型调压室两种体型进行了数值模拟,两种体型的调压室断面积相同。计算工况为双机甩负荷工况和一台机满载另一台机启动工况(以下简称甩负荷工况和启动工况),并通过对比其调压室涌浪和内部流态等得到较优的调压室断面形状,为工程实践提供参考。
2 一维MOC计算模型
2.1 有压管道的特征线法有压管道弹性水锤的基本方程由运动过程和连续性方程组成:

式中:V为管道中的流速,由上游流向下游为正;t为时间;x为距离管道最左端的距离;g为重力加速度;f为沿程损失系数;D为管道直径;H为水头;a为水锤波波速。
采用MOC方法将公式转换为两组特征线上的常微分方程,如下所示

式中:HP为测压水头;SA和SB为截面周长;QP为流量。
特征线法可以解决多种边界问题,不仅可以合理地反映水电站管路布置特点,也可以方便地考虑水流惯性、管壁弹性及摩阻的影响,便于编程实现计算机求解。
2.2 调压室计算模型Topsys-TP是武汉大学开发的水电站过渡过程一维计算软件[10-11],已成功应用于国内外近百座水电站的设计。本文采用Topsys进行一维计算,其计算模型如图1所示。T型调压室(图2)和π型调压室(图3)的算法相同,边界条件有所差异。下面以T型调压室为例,介绍其数学模型。
以国内某水电站的T 型阻抗式调压室为原型,可列出13个未知数HP1、HP2、HP3、HP4、QP1、QP2、QP3、QP4、HTP1、HTP2、QTP1、QTP2、Z,对应的边界条件是:

图1 Topsys计算简图
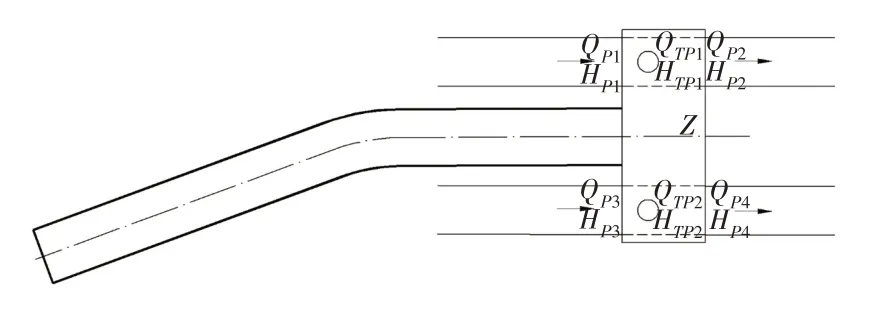
图2 T型截面调压室模型

图3 π型截面调压室模型
特征线方程:
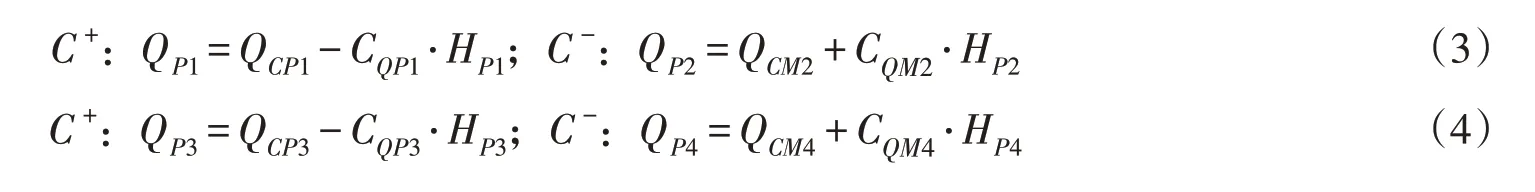
调压室水位方程:
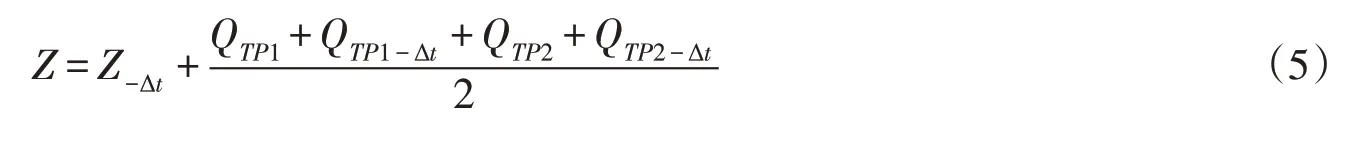
能量方程:
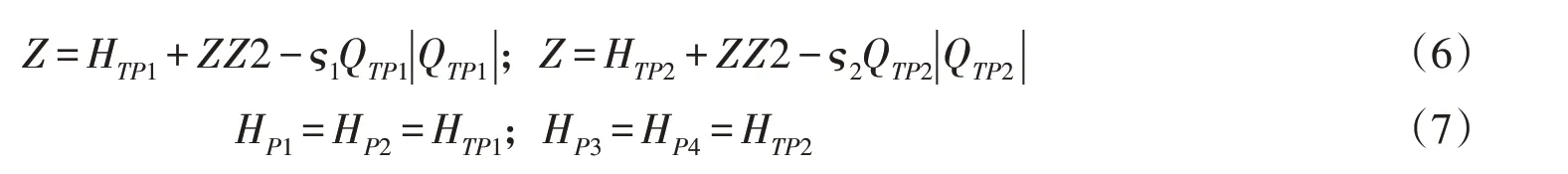
连续性方程:

式中:QP1、QP2、QP3、QP4、QTP1和QTP2为对应位置的流量;HP1、HP2、HP3、HP4和HTP1为压力水头;Z为调压室底板高程;QCP、CQP、QCM和CQM为上一时刻的已知量。
通过求解以上方程,可得到各个物理量的值。
而π型调压室中间设置隔板,隔板上设置4个连通孔,当水位低于94 m时,调压室分为2个独立的调压室,当水位高于94 m时,两侧通过连通孔实现水流交换,采用堰流公式进行计算。
3 CFD数值计算模型
3.1 有压管道的特征线法有压管道弹性水锤的基本方程由运动过程和连续性方程组成:
直角坐标系下质量守恒方程(连续性方程)的微分形式为:

若流体流速较小不考虑其可压缩性时,流体的密度为常数,上述微分方程可改为:

动量守恒方程即N-S方程,若在流动过程中流体密度和黏性保持不变,其动量守恒方程表达式为:

Realizablek-ε模型在模拟强逆压力梯度、射流扩散率、分离、回流、旋转上有较高精度,在水电站过渡过程计算中与试验数据吻合性较好[13-16]。其湍动能k及耗散率ε输运方程为:

其中:
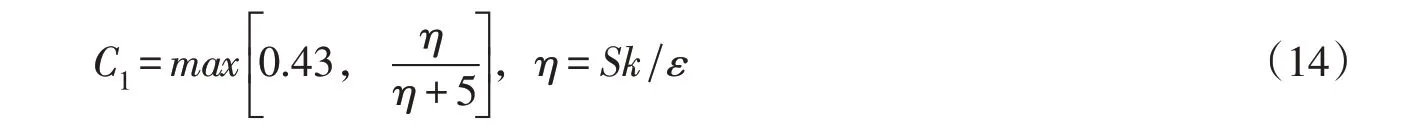
式中:ρ为密度;Gk和Gb为剪切产生项;ut为湍动黏度;YM为可压缩湍流脉动膨胀对总的耗散率的影响;C1ε、C2、σk、σε作为默认值常数,C1ε=1.44,C2=1.92,σk=1.0,σε=1.3。
3.2 计算模型与边界条件某水电站上游调压室为阻抗式调压室,水头低,调压室稳定断面积大,受地形限制无法设置双调压室,因此设置长上室补充调压室稳定断面积,长上室底面设置一定的坡度。在满足调压室稳定断面面积的前提下,考虑地形因素和水力条件,调压室横截面设计为T型和π型,如图4所示。该水电站调压室大井由开敞段和隧洞段组成,T型调压室大井由直方形开敞段及一条长隧洞组成,π型调压室大井由直方形开敞段和两条隧洞组成,开敞段中间设置隔墙分离,隔墙上设置4个连通孔。调压室底板高程87 m,总高度35 m,连接管直径7 m,长度31 m,计算管道长711.375 m。
采用Star-CCM+进行网格划分和数值计算,其可自动生成高质量的多面体网格,网格最大值设置为1.0 m,连接管及大井敞开段进行网格加密(图3),总网格数67.52万。根据上游水库水位将入口设置为压力入口。出口设置为质量流量出口,质量流量曲线由Topsys导出。调压室顶部设置为压力出口,相对压力为0 atm。湍流模型采用Realizablek-ε,固壁边界设置为无滑移壁面,近壁区采用标准壁面函数法处理。
调压室涌浪水位的监测点设置在距离阻抗孔一定距离的位置,左右对称各设置3个监测点,距底板3 m,监测其静压值P,并取其平均值计算调压室水位,两种体型监测点位置相同,监测量通过公式Z=P/9810+Z0转化为压力值,其中Z0位监测点高程。

图4 CFD模型图
4 计算结果与分析
4.1 两种体型一维大波动计算结果与分析导叶开启规律和导叶关闭规律如图5和图6所示,一维大波动计算结果如图7—13所示。由图7可以看出,甩负荷工况下,T型调压室和π型调压室的涌浪波动规律相同,均随时间做周期性衰减。由图8可以看出,启动工况下,由于水位低于100 m,π型调压室分为两个单独的调压室,Unit2机组正常运行,因此水位不变;Unit1机组由空载启动,受到调压室稳定断面积限制,Unit1 机组侧的最高涌浪比T 型调压室高0.34 m,最低涌浪低1.78 m,最小淹没水深为3.35 m,但其衰减速度较快。因此三维计算需重点关注π 型调压室在启动工况下调压室的流态。

图5 机组导叶开启规律示意

图6 机组导叶关闭规律示意

图7 甩负荷工况调压室涌浪波动
图9为甩负荷工况下调压室底板压差,从图中可以看出,两种体型的调压室底板压差随时间变化规律相同,向上最大为15 m 左右,向下最大为2 m 左右,且向上和向下最大压差出现的时间相近。启动工况下(图10),T型调压室Unit2机组侧在0.02 s出现向下最大压差为5.32 m。图11—13的调保参数波动图,两种体型相差较小,且均在调保参数控制范围以内。
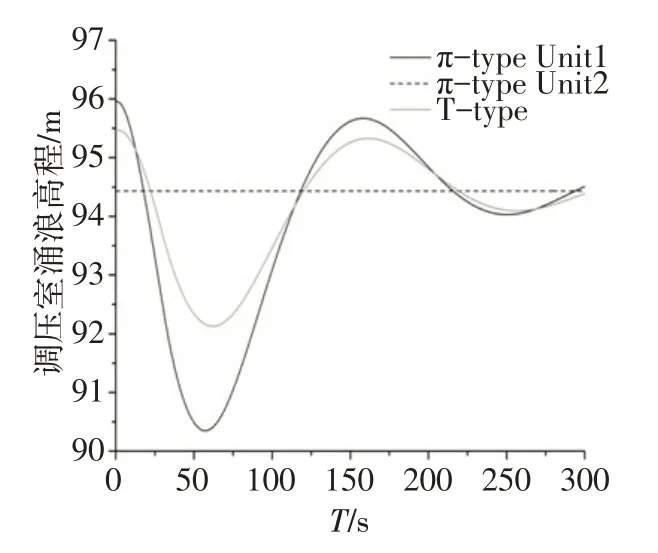
图8 启动工况调压室涌浪波动
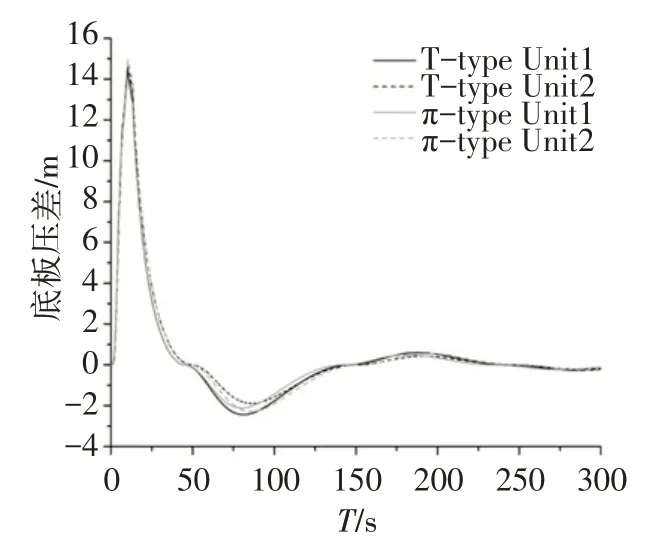
图9 甩负荷工况底板压差

图10 启动工况底板压差

图11 甩负荷工况蜗壳出口最大动水压力
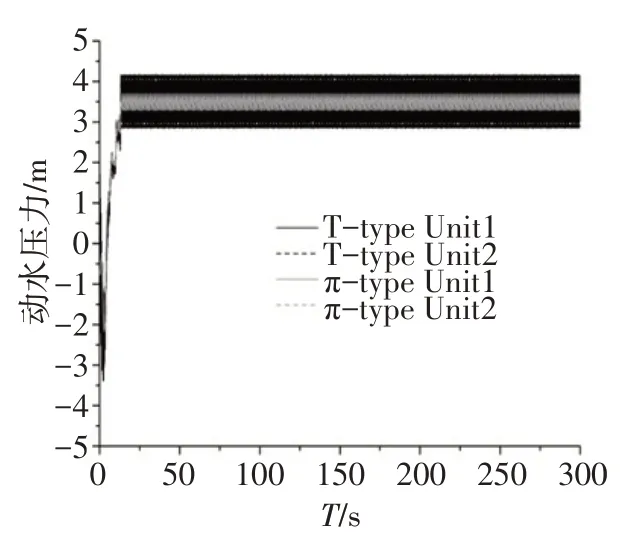
图12 甩负荷工况尾水管最小动水压力
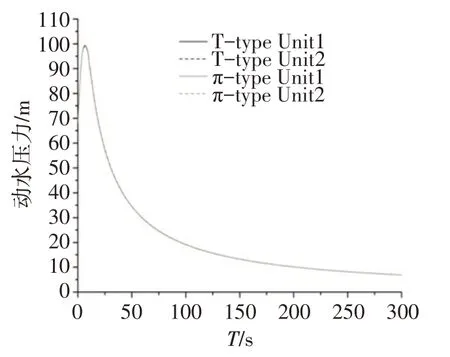
图13 甩负荷工况转速波动
4.2 一维与三维调压室涌浪对比分析表1为一维与三维调压室最高/最低涌浪及周期的对比图,图14和图15为一维与三维涌浪水位随时间波动的对比。从表1可以看出:由于三维计算调压室水面的不规则波动,曲线图出现了次波峰波谷,但一维和三维的曲线图整体波动趋势相同。由表1初始水位的对比可知,两种工况两种体型下,一维计算的初始水位比三维水位高,最大差值为0.22m,是由于一维三维计算的沿程损失差值造成的,可通过调整管道糙率减小两者差值,目前计算的差值在误差范围内。通过对比表1两种体型的一维和三维最高/最低涌浪以及周期可知:甩负荷工况下,一维和三维最高涌浪最大差值为1.41 m,最低涌浪差值最大为0.3 m;启动工况下,一维与三维的最高涌浪和最低涌浪的差值均在1 m以内。由于三维计算水面波动的不平稳性,一维与三维的周期差值无明显规律,但结合图14和图15可以看出,一维与三维的波动曲线变化趋势和衰减速度吻合程度较高。因此,一维计算和三维计算的计算方法是可靠的。
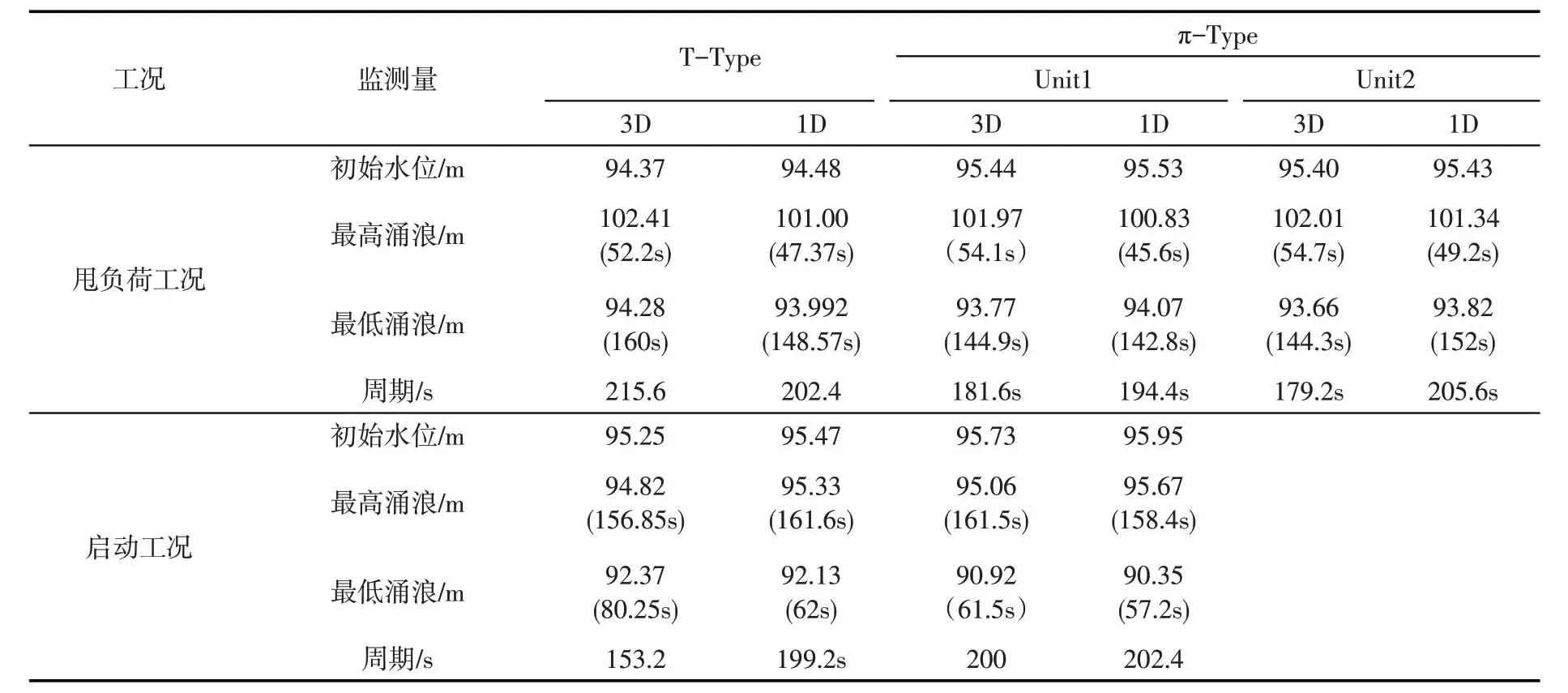
表1 调压室涌浪对比
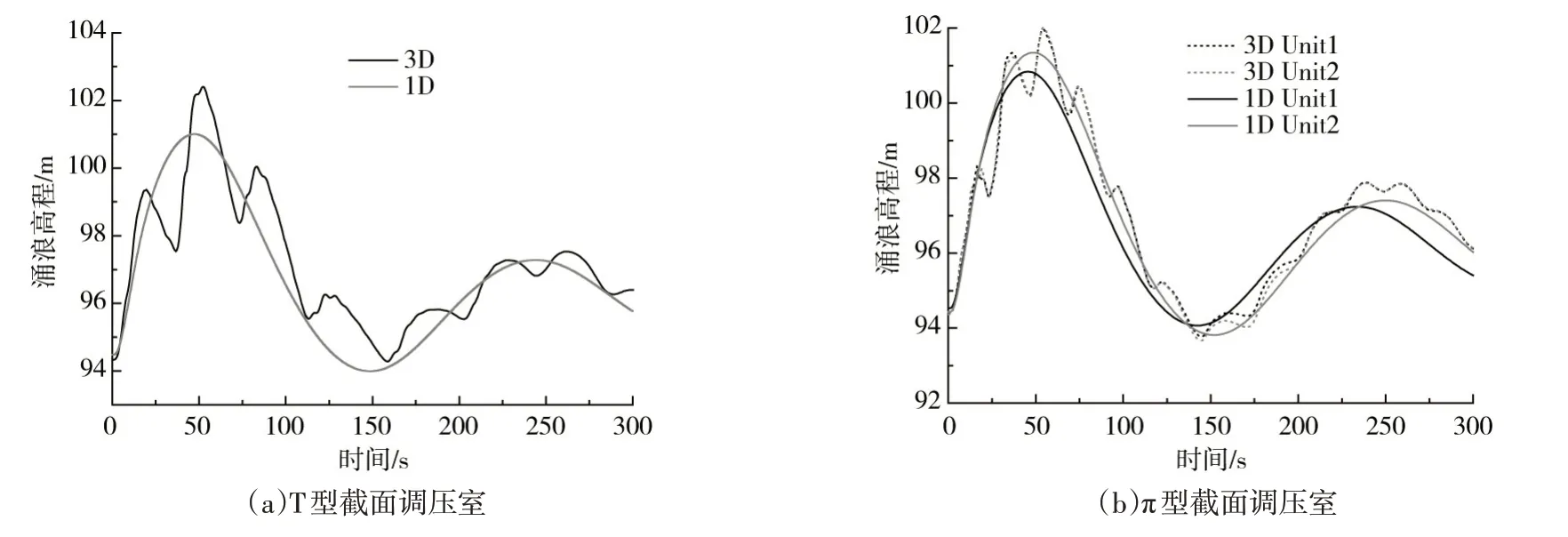
图14 甩负荷工况涌浪波动

图15 启动工况的涌浪波动
4.3 三维计算流态分析阻抗式调压室容易产生立轴旋涡[20],贯穿型立轴旋涡将会对机组及输水管道造成严重影响,破坏水体正常流态,引起空化和振动等。为了研究两种体型调压室的液面波动形态以及是否会产生立轴旋涡,对其波动水面进行监测,结果如图16—19所示。
图16和图17为甩负荷工况下调压室的液面波动情况。甩负荷开始时(即t=0 s时刻),T型调压室和π 型调压室水面稳定。甩负荷开始后,机组导叶迅速关闭并在13 s 时全部关闭,机组引用流量减少,有压隧洞中的水流涌向调压室,调压室大井阻抗孔上方出现鼓包形状,由于T型调压室上室较长,长上室内产生了较大的水面波动,π型调压室两个长上室内水流呈现梯度流动,未出现较大的波动。甩负荷工况下,仅在甩负荷初始阶段流入调压室流量较大时,调压室液面扰动剧烈,甩负荷结束后,调压室内平面趋于平稳。
两种体型启动工况下调压室的液面波动如图18和图19所示,初始时刻,Unit2 机组满负载运行,π型调压室Unit2侧水面较低,Unit1侧调压室通过下方两个连通孔向另一侧补充水流。Unit1机组启动后,Unit1机组引用流量增加,上游调压室补充隧洞中的水流,调压室液面下降。T型调压室的长上室位于两阻抗孔中间位置,Unit1 机组启动初始阶段,长上室的水流来不及补充Unit1 侧,而此时流出调压室流量较大,在阻抗孔上方形成了吸气旋涡,吸气旋涡迅速蔓延到升管内(图18(b))。对于π型调压室,由于长上室位于阻抗孔中心线上,流出调压室流量较大时,长上室内水流可迅速进行补充,水面下降较为平稳。

图16 甩负荷工况下T型调压室水面波动图

图17 甩负荷工况下π型调压室水面波动图
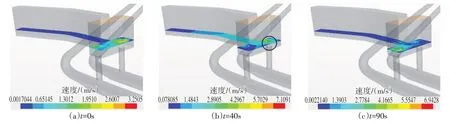
图18 启动工况下T型调压室水面波动图
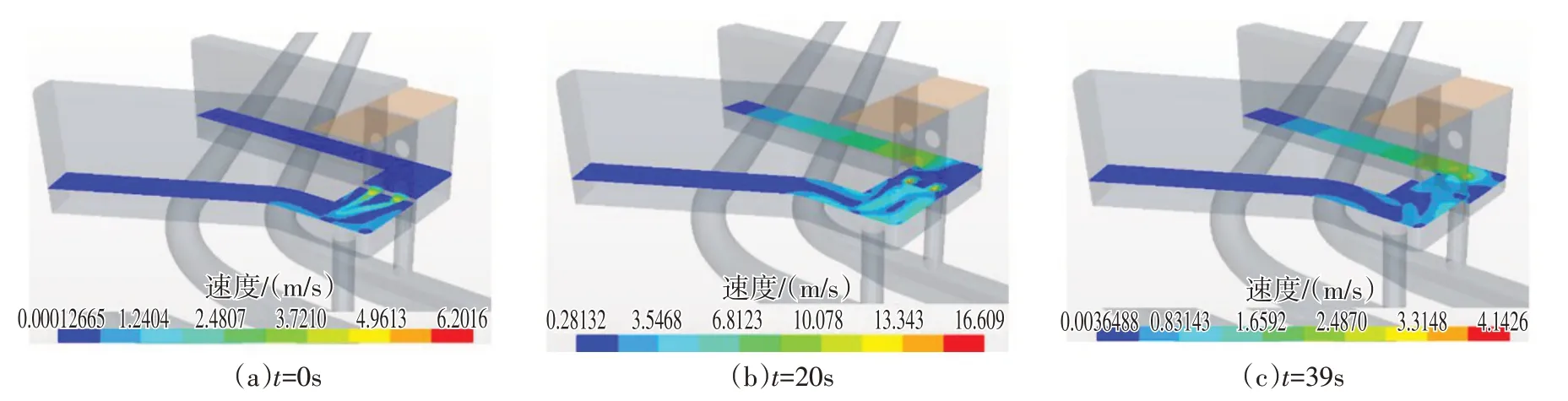
图19 启动工况下π型调压室水面波动图

图20 启动工况下T型调压室水平截面速度矢量图(t=20s)

图21 启动工况下π型调压室水平截面速度矢量图(t=20s)
为了进一步分析T型调压室吸气旋涡产生的原因,对两种体型调压室的水平截面速度矢量图进行了对比,如图20和图21所示,水平截面距离调压室底板3 m。由图20可知,Unit1机组启动后,T型调压室长上室中的水流流向Unit1 侧阻抗孔,并沿逆时针方向进入阻抗孔,由于上室较长,坡度较小,其尾部段水流基本为死水,在过渡过程后期会由于压差缓慢流向调压室大井。π型调压室在过渡过程的初始阶段,长上室中水流直线流向阻抗孔,调压室大井内水流也径直向阻抗孔位置汇聚,未形成明显的速度环量。
4.4 两种体型对比与分析通过以上对比分析得出,T型调压室在启动工况产生了吸气旋涡,而π型调压室水流状态较好,原因如下:(1)速度环量。T型调压室的阻抗孔位于长上室两侧,当流出调压室流量较大时,长上室中的水流会顺时针或逆时针流入阻抗孔中,在其上方形成速度环量。π型调压室两长上室位于阻抗孔中心位置,长上室中的水流可径直进行补充,无法形成速度环量。(2)流量变化。T型和π型调压室的长上室宽度比为0.58(如图22),其高度相同,因此在相同条件下,π 型调压室的过流面积远远大于T 型调压室,T 型调压室长上室的流量无法及时补充调压室大井的流量会导致阻抗孔上方出现短时间的液面塌陷。(3)淹没水深。启动条件下的最小淹没深度为3~4 m,较小的淹没水深也是形成吸气涡旋的重要原因。流量变化大,较强的速度环量,淹没水深较小,都是形成吸气漩涡的决定性因素。T 型调压室方案在水位下降时出现强烈的吸气漩涡并延伸至升管,而π型调压室则未出现吸气旋涡。因此从瞬态水力特性角度来看,π 型调压室方案优于T 型调压室方案。

图22 两种方案过流面积比
5 结论
本文采用一维和三维数值模拟对T型调压室和π型调压室的过渡过程进行了对比分析,并对三维计算的调压室局部流态进行了分析,结论如下:(1)甩负荷工况和一台机满载另一台机增负荷的过渡过程中,一维和三维计算的调压室涌浪波动曲线波动趋势相同,均随时间周期性衰减,涌浪极值的差值均在1.5 m以内,验证了CFD计算的可靠性。(2)T型截面调压室在启动工况水位下降时调压室的淹没水深较小,长上室中的水流补充阻抗孔上方的水流时呈顺时针或逆时针流入,导致吸气漩涡的产生;而π型调压室由于长上室内水流的即时补充,不具备产生吸气旋涡的条件,因此从水力学条件上,π型调压室方案优于T型调压室方案。
