神经网络的四旋翼无人机输出反馈控制器设计

大同煤炭职业技术学院 王 奇

本文提出了一种基于神经网络和输出反馈的四旋翼无人机非线性控制器设计方案。在该方案中仅使用四个控制输入就可以控制无人机的六个自由度。此外，还引入了神经网络观测器来预测无人机的平动速度和角速度，其中仅考虑无人机的位置和姿态是可测量的。利用李雅普诺夫理论证明，位置、方向和速度跟踪误差，虚拟控制和观测器估计误差，在存在有界扰动和神经网络函数重构误差的情况下，每个神经网络的权值估计误差都是半全局一致最终有界的。在存在未知非线性动力学和干扰的情况下，证明了所提出的输出反馈控制方案的有效性。

1 四旋翼无人机动力学

无人机的控制输入u1和u2分别为转子角速度产生的推力和扭矩，可以通过推力和阻力系数进行计算，表述如下：

在式(1)中d为正标量，表示从四转子中心到转子轴的距离，Ct表示推力因子的正标量，Cd是表示阻力因子的正标量。一旦确定了无人机的控制输入，可以使用式(1)中的关系来确定所需的转子转速，以获得所需的推力和旋转扭矩。根据式(1)可知，每个转子的状态与总推力和旋转扭矩有关。因此，在建模过程中中，每个转子处叶片拍动的影响将组合为四转子动力学的单一非线性扰动。对于平动速度，叶片拍打导致推力纵向重定向，同时提升力减小。因此，在x轴和y轴方向上的扰动被建模为TL x，y=TI sinα，在z轴方向上的推力减小被建模为TL z=TI(1-cosα)，角速度矢量的扰动被描述为MH=Kα。

2 控制器设计

无人机的总体控制目标是跟踪期望轨迹和期望偏航，同时保持稳定的飞行配置。完成控制目标需要具备无人机动力学和速度相关的完整信息，但是在这项工作中，横坐标和角速度是无法直接测量的，所以动力学的完整信息不可用。因此，神经网络的普适逼近特性被用于观测器、虚拟控制器和动态控制器的设计。动态控制律需要了解质量，而观测器需要了解质量和惯性矩。所提出的神经网络观测器估计控制回路所需的无人机速度矢量。控制回路由运动学控制器、神经网络虚拟控制器和神经网络动态控制器组成，利用观测器提供的信息生成相应的指令以完成控制目标。

首先需要推导出神经网络虚拟控制器使用的参数。即计算期望的平移速度，以确保无人机位置收敛到期望的轨迹。接下来找到所需的俯仰角和横滚角，以确保无人机平移速度的x轴和y轴分量跟踪各自的所需值。然后，给定所需的方向，然后计算所需的角速度，为了开始无人机跟踪控制器的开发，我们首先定义位置和平移速度的跟踪误差。对于无人机位置，由如下公式描述：

根据选择所需的速度以稳定位置误差和平动速度跟踪误差，如下式所示：

将参数ev代入到Vd中并观察v=Vd-ev的值，闭环位置误差动态可定义为：

现在根据期望的方向角θd定义Rd=R(θd)。最后可以得到三个方向的平动速度误差，其中v1是平移速度的观测器估计，如下式所示：

误差参数evx和evy无法直接通过使用控制输入u1进行控制。evx和evy必须在已经被控制输入u1或u2影响的状态来间接进行控制。俯仰和滚转分别用于控制无人机沿x轴和y轴方向的平移运动，因此，俯仰和滚转角度被视为式(5)中无人机误差动力学欠驱动部分的虚拟控制输入。

3 仿真结果

四旋翼无人机现在考虑存在未建模的动力学，如空气动力学阻尼和叶片拍动，并验证了本工作中开发的神经网络输出反馈控制律的有效性。此外，还添加了随机干扰，并在Matlab中进行了仿真。其中阻尼系数选择如下：

叶片拍动参数为K=0.75N-m/rad，仿真开始时转动角α=0°，在时间t=20s时从0°转动到20°。无人机跟踪所需的位置和偏航角如下式所示，无人机的质量设定为m=0.9kg，转动惯量J={0.32，0.42，0.63}kg·m2。

每个神经网络采用五个隐层神经元，并选择控制增益进行优化，取值如下：

Ko=[23，60，20]，KΩ=[24，80，20]，Kv=[10，10，30]，Kρ=[10，10，30]，Kθ=[30，30，30]，Kw=[25，25，25]。为了满足所提出的约束条件，神经网络的参数选择如下：Fo=10，FΩ=40，Fc=20。在仿真中，所有可调神经网络权重初始化为0，而位置和方向的初始观测器估计值设置为无人机的初始位置。

检查轨迹图期望轨迹从原点开始，而无人机从上述初始配置开始，无人机快速收敛到期望航向，并以较小的有界误差跟踪，在20s时，在误差图中观察到一个小峰值，对应于引入的外部干扰。神经网络控制器快速适应变化的条件，无人机返回到其所需路径并且成功跟踪所需轨迹，神经网络虚拟控制器生成的理论方向正确引导UAV沿所需路径飞行。图1显示了位置的跟踪误差，每个观测到的误差收敛到原点周围的一个小边界区域。在20s时外部干扰的影响是非常明显的，同时可以观察到即使干扰本身没有消失，每个跟踪误差也会迅速返回到零。并且神经网络会进行调整，以便恢复可接受的跟踪性能。平移速度的跟踪性能再次增强了虚拟控制器结构计算实现跟踪所需的适当俯仰角和滚转角的能力。

图1 跟踪误差

图2显示了位置的观测器估计误差，观测到这些误差收敛到原点附近的一个小有界区域。在剩下的模拟中，观察到图2中的最大观测器位置误差小于0.03。在引入有界干扰后，在y轴坐标估计中观察到最大误差为0.03。当引入未知非线性时，观测器估计误差最初增大，当神经网络观测器开始补偿非线性时，观测器估计误差减小。此外，通过仿真计算出的观测器位置估计误差的上界为0.0303。通过总结每个跟踪误差和观测器估计误差的均方误差和最大观测误差。在每种情况下的均方误差都很小。这一结果与图2中观察到的跟踪和估计性能一致。此外，跟踪和观测器估计误差的最大值出现在模拟开始时，或在引入外部干扰后直接出现。在图2的误差图中也观察到了这种现象。

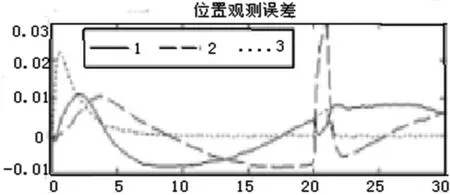
图2 观测器估计误差

结论：针对欠驱动四旋翼无人机，提出了一种新的神经网络输出反馈控制律，该控制律利用欠驱动系统的自然约束产生虚拟控制输入，保证无人机跟踪期望轨迹。利用自适应反推技术，在存在未建模动力学和有界干扰的情况下，仅使用四个控制输入即可成功跟踪所有六个自由度。提出了一种神经网络虚拟控制结构，该结构允许使用无人机的俯仰和横摇来控制期望的平动速度。并利用神经网络计算无人机动态系统的实际控制输入。利用李亚普洛夫理论，证明了每个神经网络、观测器、虚拟控制器以及位置、方向和速度跟踪误差的估计误差均为半全局一致最终有界。通过仿真结果证实了理论推测，以及无人机在未建模动力学和有界干扰情况下的跟踪能力。该控制器的性能优于传统的线性控制器。