变尺度随机共振理论在应答器信号检测中的仿真研究
2021-02-28湖南铁道职业技术学院蔡小成
湖南铁道职业技术学院 蔡小成
中国铁路兰州局集团公司嘉峪关电务段 黄正红
应答器作为高速铁路列车运行控制系统中的重要基础设备,向列车传递线路速度、坡度、过分相以及定位信息,保证着列车运行的高效性和安全性。应答器向车载设备发送的上行链路信号较弱,加之列车运行环境复杂,精确的检测应答器向列车发送的上行链路信号对于保证列车安全运行非常重要。
目前车载查询器对于接收到的上行链路信息大多采用传统的非相干正交解调法、相干解调法、差分解调法以及离散短时傅里叶变换等方法,传统的检测方法都立足于对噪声信号的抑制或滤除,这些方法在抑制噪声信号的同时也在一定程度上削弱了有用的特征信号;本文提出利用混沌振子系统实现应答器信号的检测,但是该种方法的检测精度受系统临界阈值所限定。基于随机共振理论对微弱信号检测是一种新方法,该方法不采取直接降噪的方式,而是通过信号、非线性系统、噪声三者之间的最佳匹配使系统输出达到最优,实现噪声能量向信号能量的转换,并且在故障诊断、图像处理以及信号处理等领域得到了良好应用。
本文根据应答器上行链路2FSK信号的特征,进行归一化变尺度处理,使其满足随机共振系统对微弱信号检测的要求,利用MATLAB进行仿真,准确的获得了检测信号的频谱曲线。
1 随机共振理论检测微弱信号
利用随机共振理论实现信号检测不采取直接降噪方式,而是通过信号、非线性系统、噪声三者之间的最佳匹配使系统输出达到最优,实现噪声能量向信号能量的转化,从而增强或识别噪声背景下的微弱特征信息。随机共振现象可基于统计力学模型进一步解释,单位质量布朗粒子同时受高斯白噪声和特征信号作用时的过阻尼运动,经典双稳态系统随机共振模型的数学表达式如式(1)所示。
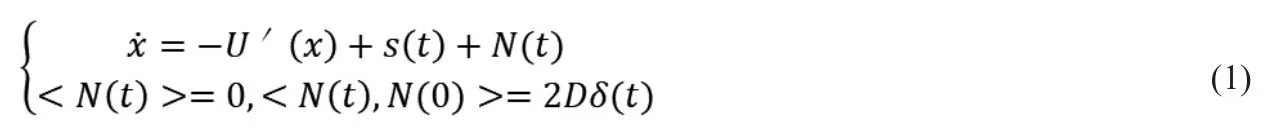
其中,U(x)为非线性的势函数;S(t)为微弱特征信号;N(t)为高斯白噪声;δ(t)表示狄拉克δ函数;D为噪声强度;x为系统输出。
典型的双稳态势函数如式(2)所示:


当式(1)中同时含有微弱外部周期信号和噪声激励且信号赋值A<Ac时,周期信号有道系统势阱做周期性切换。在噪声作用协助下,布朗粒子有可能跃过势垒逃逸到另一个势阱中。噪声强度太小时布朗粒子跃迁概率低,噪声强度太大时布朗粒子跃迁过于频繁。只有当噪声强度、信号和非线性系统达到协同作用时,才能发生周期性跃迁从而转化噪声能量为信号能量。
所以选择合适的系统参数,使噪声强度、信号和非线性系统达到协同时,利用噪声能量转化为信号能量这一规律,可以实现微弱信号的检测。
2 应答器信号的变尺度随机共振检测
2.1 应答器信号特征
应答器信号是一种相位连续、中心频率为4.234 MHz的调制信号,其调制频偏是282 kHz,调制速率为564 kb/s,其基本表达式如式(4)所示。

其中,As是2FSK信号的载波幅值;f0为载波中心频率;Δf是频偏;Vm(t)为取值为±1的二进制输入调制信号。即当传送码元“0”时,发送载频为3.948 MHz,当传送码元“1”时,发送载频为4.512 MHz,具体参数如表1所示。

表1 应答器上行链路信号参数
2.2 应答器信号归一化变尺度处理
经典随机共振理论只适用于处理弱噪声背景下的慢变特征信息,即特征信息的频谱远远小于1。然而,应答器信号2SFSK(t)属于快变特征信息,即,必须将该信号进行归一化变尺度处理,使其满足经典随机共振理论的要求。
因此将式(4)代入式(1)中,则受应答器信号激励的随机共振系统模型如式(5)所示。
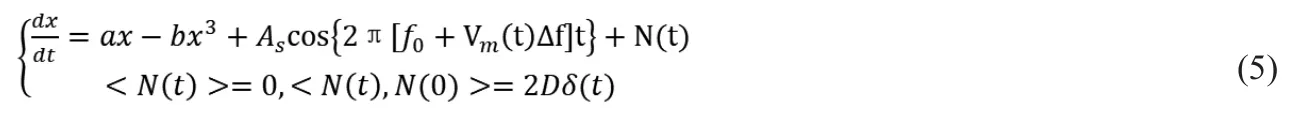
引入替换变量:

将替换变量(6)代入式(5)中,整理得到式(7)。

式(7)是式(5)的归一化标准形式,式(5)为高频激励信号对应的大参数随机共振系统,式(7)为高频信号转化为低频信号后对应的小参数系统。因此,较大的参数a可以将高频信号转化为低频信号,从而满足经典随机共振理论。然而,考虑到变尺度前后激励幅值的等价性,归一化变尺度以后需将信号和噪声同时乘上比例因子,则式(7)转化为式(8)。
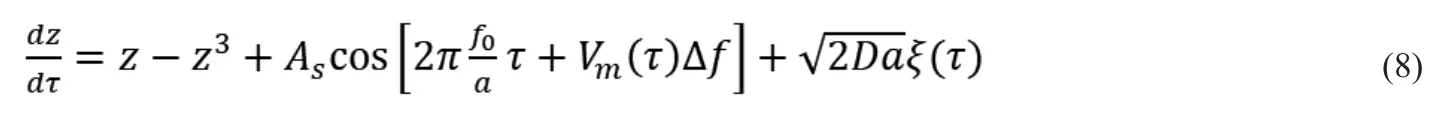
式(8)为经典随机共振模型,其由(5)中的系统参数a和b归一化得到,如果系统参数a=m,m取值足够大,则高频信号对应的低频信号就可利用式(8)中的小参数系统进行随机共振处理,因此选择合适的参数a(或m),利用归一化变尺度随机共振方法能够增强并检测任意高频信号。
3 信号检查仿真及结果分析
利用MATLAB平台,模拟应答器2FSK信号调制,根据应答器信号特征设置载波频率f0=4.243MHz,频偏Δf=282.24kHz,初始相位为0,赋值As= 1,采样频率fs= 2.4×109,调制生成2FSK信号时域波形如图1所示。
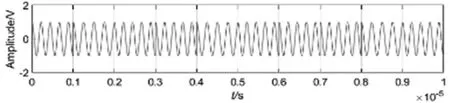
图1 2FSK信号时域波形图
在该信号中加入高斯白噪声模拟传输信道噪声,信噪比SNR=-20dB,混入噪声的信号时域波形如图2所示,频域图如图3所示。从图2和图3可以看出,调制后的2FSK信号完全淹没在噪声信号中。
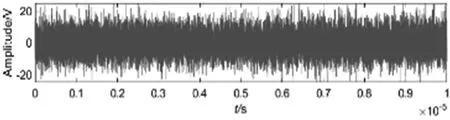
图2 带噪声的2FSK信号时域波形图
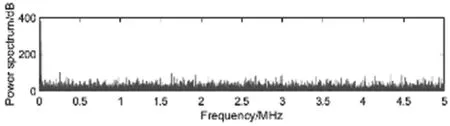
图3 带噪声的2FSK信号频域图
根据应答器信号变尺度处理理论分析可知,要是系统满足随机共振理论,要选择合适的a值,使,由于f0=4.243MHz已知,所以a应该选择远远大于f0。
本文中选择a=5×108。经双稳态系统输出的信号时域波形如图4所示,频域波形如图5所示。由图4和图5可以看出,应答器上行链路信号在时域中得到了较好的还原;在频域中噪声能量显著削弱,有用输入信号得到了增强,利用随机共振理论能够实现应答器信号的检测。
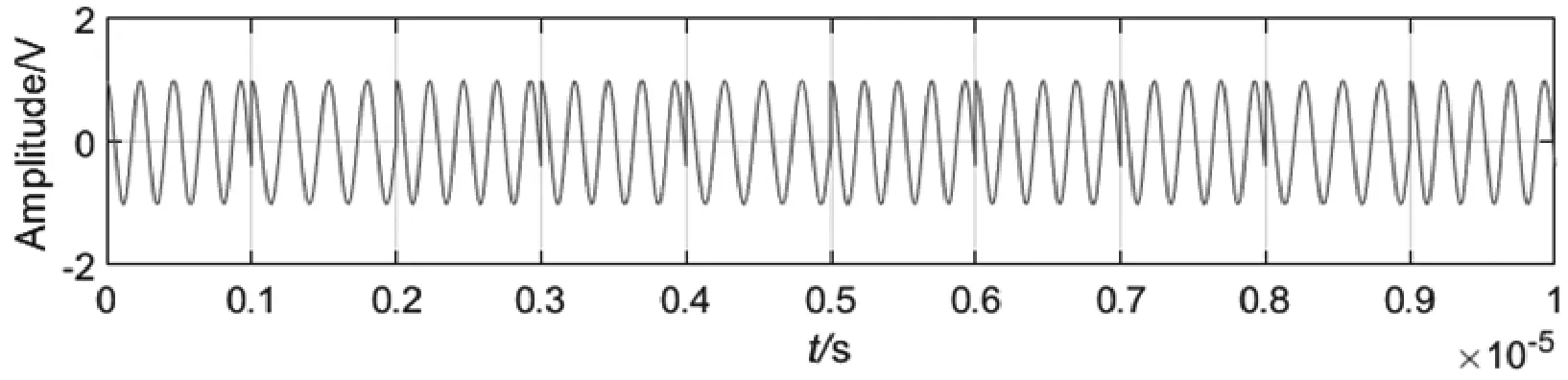
图4 输出信号时域波形图
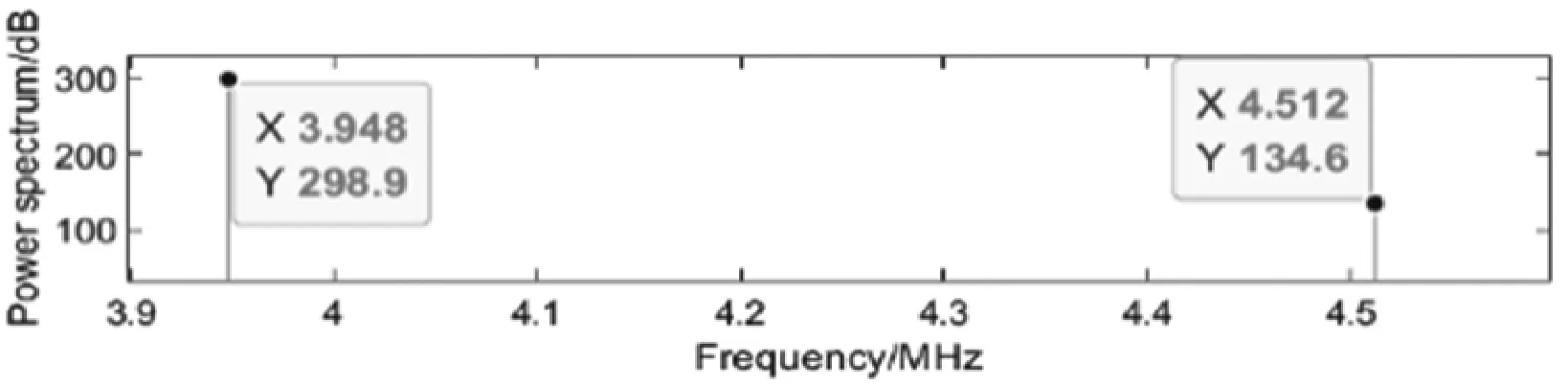
图5 输出信号频域波形图
结论:根据应答器上行链路2FSK载波信号的特征,将其进行归一化变尺度处理后,使满足经典随机共振理论。并选择合适的系统参数,使特征信号、噪声以及双稳态系统达到最佳匹配,可以使噪声能量转化为应答器载波信号能量,能够精确的检测出被淹没在噪声环境中的应答器上行链路信号。
