电缆故障点定位中小波分析应用的研究

沈阳工程学院 张家航 王存旭

电力电缆线路在供电过程中，尤其是在输电配电环节，一直起着无可替代的作用。如何在电缆发生故障时及时、准确地发现故障并检测出故障点的位置，是电缆发生故障时及时修复故障的关键。因此，为了满足电力系统和用户对供电可靠性的要求，及时修复电缆故障是非常必要的。对比于傅里叶变换，小波分析最大的优点在于它能同时解决小波信号在时域和频域中傅里叶无法解决的两个局部特征。因此，在电缆故障检测过程中，可以利用matlab建立模型，然后对故障行波进行小波分解、处理和重构，确定电缆故障的具体位置。本文主要归纳了小波分析的基本理论思想，分析了小波分析在电力线路故障诊断中的几种实际应用。通过理论分析，明确了应用小波进行电缆故障信号去噪理论的适用性。

1 小波分析基本理论

如果ψ∈L2(R)满足允许性条件：

2 小波分析在电缆故障诊断中的应用

2.1 基于小波分析的电缆故障选线

在大型输变电系统中，同一母线可能有多回出线。为了充分满足大型电力系统在供电运行过程中对于经济性的要求，安装的行波线路故障信号测距装置必须能够同时监测多回输电线路。当电力线路发生故障之后，每一回电力线路的行波启动元件都存在着启动的可能性，因此在发生电力电缆线路故障时，进行准确无误的故障选线是十分必要的。基于幅值考虑，一般来说，正常电力线路的行波信号只包含一个透射分量。在实际操作中进行电力系统故障线路选线的主要依据为：正常情况下电力系统的输电线路经过小波分析后，输电线路行波信号的模极大值会呈现出下降趋势，而输电线路一旦发生故障，这一回输电线路的行波信号经过小波变化的模极大值会变大，工作人员可通过对模极大值进行比较来对输电线路进行故障选线，模极大值最大的线路即为故障线路。

2.2 基于小波分析的电缆故障信号奇异性检测的研究

实验分析过程中获取一有明显拐点的信号，通过选用恰当的小波对这一阶跃信号进行多层分解可得到信号的突变点时刻，以此来验证小波变换在电缆故障情形中应用的适用性。细节信号如图1所示。

图1 细节信号

从图1中可以得出，在小波分解得到的细节信号波形中在t=100处有一个明显的阶跃变化，它是一个典型的阶跃信号。因此，电力线路故障信号经过小波的多尺度分析之后获得的结果可用来进行电力电缆故障信号奇异点的研究。电力电缆线路的故障信号经过多尺度小波分析后得到的结果具有模极大值。可根据模极大值推算出电力故障信号波形的奇异点。因此，将小波分析应用于电缆故障线路反射信号的奇异点检测可用来明确电力电缆的发生故障的初始时刻以及判断出故障点的位置所在。

2.3 基于传统小波阈值规则的电缆故障波形去噪研究

小波变换消除电缆故障信号噪声干扰的关键是阈值的选择，选择合适的阈值对消除典型电缆故障噪声具有重要意义。下面给出两种在分析中常见的阈值规则。

（1）Stein无偏似然估计阈值T1(rigrsure规则)

设一向量W=[w1,w2, ...,wn]，且w1≤w2≤ ... ≤wn,n的含义同上。再设风险向量R，其元素为：

将R中的最小元素rb设为风险值，通过b能够推算向量W对应的wb，阈值wb可表示为：

（2）最大最小准则阈值T2(minimax规则)：

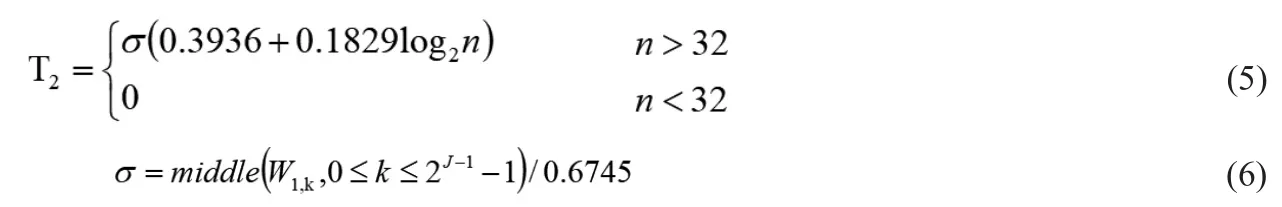
上述公式中，σ为噪声信号的标准差，n为噪声信号系数个数总和，W1,k为尺度等于1的小波系数。

含噪波形是原始波形加入白噪声获得，该原始信号具备较多的信号干扰，原始含噪波形经过最大最小准则阈值分析处理后可达到图2所示去噪效果，经过分析可知该方法对电缆故障反射波形的去噪效果良好，有明显的消噪效果。但如果想达到更高的精密度还需要在原有算法的基础上做进一步的改进研究。

图2 最大最小准则阈值去噪效果波形

3 结语

本文主要针对小波分析在电力电缆故障诊断中几种常见的应用情形，研究了小波变换在这几种电缆故障检测实例中应用的适用性，包括电力电缆故障线检测、电力电缆故障信号的奇异性检测和含噪声反射波形的噪声消除等。电力电缆故障行波信号经过小波分析处理后获得的奇异点往往携带着可用于电力线路故障检测的重要信息。精准定位电力电缆故障点位置所在的关键在于检测出电缆行波信号的奇异点与模极大值这两个主要特征，而小波变换所具有的时频局部化的特性刚好可用来检测这两个用来检测电力线路故障的特征值。因此，小波变换在电缆故障诊断方面得到了很好的应用，但任然存在一些不足之处。如何完善这些不足之处是未来工作的重点。