基于余弦相似度的改进ORB匹配算法

成 怡 ，朱伟康 ，徐国伟

（1.天津工业大学 电气工程与自动化学院，天津300387；2.天津工业大学天津市电工电能新技术重点实验室，天津300387）

目前，许多图像特征点匹配算法都在使用二进制特征描述符，例如 BRIEF[1]、ORB[2]和 DAISY[3]等算法，这是因为它们相比于SIFT[4]、ASIFT[5]和SURF[6]这类使用梯度描述符的算法，拥有计算量少、存储更紧凑的优点。二进制特征描述符通常采用汉明距离（Hamming distance）匹配方法进行特征匹配。

汉明距离[7]是通过将2个二进制特征描述符按位做异或操作求得，所求得的结果中1的数量越少，代表2个二进制描述符越相似。它相比于欧氏距离[8]、马氏距离[9]和信息熵[10]这些相似性算法，在计算效率上远远超过后者。但是在某些特殊情况下，例如原图像和目标图像有许多相似区域时，会呈现出较高的误匹配率。即使应用 RANSAC（Random Sample Consensus）算法消除误匹配点，误匹配率仍然很高，因为汉明距离只能证明两特征点所在的邻域信息相似，但是却很难描述两点的空间几何状态和位置信息。

目前改善这个问题的方法有许多，大致可以分为3类。第1类方法就是改善局部特征描述符，让其具备空间几何状态和位置信息。例如融合全局环境描述符（integrate Global Context descriptor）[11]、嵌套 SIFT 描述符（Nested-SIFT descriptor）[12]、兴趣点对描述符（pairs of interest point descriptor）[13]、空间几何信息描述符（spatial geometric information descriptor）[14]等。以上方法可以改善这一问题，但是其特征描述符的计算往往比较繁琐，导致匹配时间增加，从而降低匹配效率。第2类方法是改进匹配算法，例如Beis等[15]提出的NN算法，通过调整阈值（最近邻向量和下一个最近邻向量之比）来削减一些误匹配。虽然该方法比较巧妙，相比于改善局部特征描述符的方法降低了计算量，但是因为其匹配阈值的变化，容易丢失一些正确的匹配点，导致遗漏正确匹配点。第3类方法是利用对极几何的约束，例如Zeng[16]提出的RANSAC方法，首先使用文献[17]中提及的K近邻算法进行粗匹配，然后使用全局拓扑相似性约束条件筛选出精确匹配关系。该方法能从包含大量局外点的数据集中估计出高精度的参数。

近年来，国内外研究者针对此问题提出了一些改进方法。例如文献[18]中提出的一种模块分割算法，利用灰度变化率和子区域特征有效因子剔除低质量图像模块和关键点。其次,针对在两帧图像匹配过程中对过多无效特征点进行匹配产生误匹配的问题,提出利用相机前一时刻位姿剔除当前帧图像中不在前一帧图像视野中的特征点。该算法意在通过对图像进行模块分割以及剔除不在前一帧图像上的特征点的方法，来弥补特征描述子没有空间几何信息的缺陷，但该方法为保证剔除特征点的正确性上，使用了较多时间，且因为剔除低质量图像模块而丢失了图像信息完整性，不能满足算法实用性。文献[19]中提出的融合颜色不变量和形状信息的图像匹配方法是通过提取特征点的主曲率信息进行全局形状描述，最后将生成的描述子与二进制描述子融合，用于特征点匹配。该算法虽然一定程度上解决了多相似区域图像特征点匹配误匹配率高的问题，但因为其引入了SIFT算法的特征点提取算法，且计算特征点曲率耗时较高，不能满足算法的实时性要求。综上，要在保证实时性的基础上提升算法性能，成为了解决该问题的关键。

本文从降低误匹配率、保持正确匹配点数角度开展研究，提出一种融合汉明距离和角度余弦不变性[20]的方法。首先利用汉明距离来测量二进制特征值的相似度，然后计算匹配向量间的角度余弦，利用角度余弦的不变性，消除那些“良好”的误匹配，最后再使用RANSAC算法消除误匹配点。本方法以期在保证算法实时性的同时，提升算法性能。

1 ORB图像特征点匹配算法

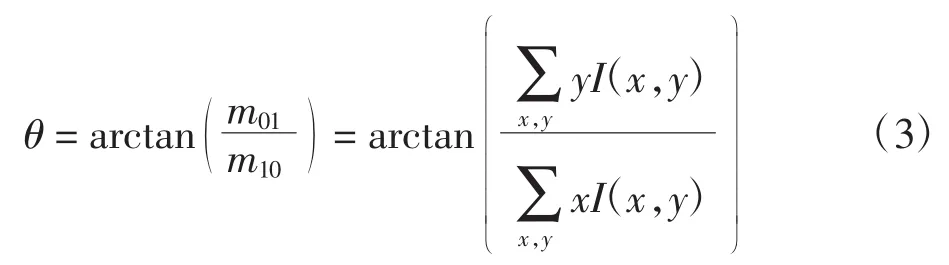
ORB图像特征点匹配算法可归纳为两个步骤：一是特征描述符的生成；二是对特征描述符进行匹配。ORB特征描述符，是将FAST特征检测和改进后的BRIEF描述符相结合的一种特征描述符。先通过FAST进行特征点检测，特征点的方向通过获取特征点附近的质心获得。文献[21]定义邻域的质心计算方法如公式（1）所示：

式中：x，y是FAST特征点的位置，邻域圆的半径为r，x，y的定义域为[-r，r]。圆形邻域内的质心计算公式如下：

FAST特征点的方向：

BRIEF描述符的主要思想是随机选择以特征点为中心，一定大小邻域内的几组点对，比较这些点对的像素的灰度值大小，并按位记录结果（前者小于后者的像素值记1，其他记0），组成一组二进制字符串作为特征点的特征描述符。但是，当图片旋转度数超过15°时，匹配的效果很差，为了增加描述符的抗旋转能力，ORB基于BRIEF描述符的生成方法进行了改进：

（1）先用oFAST算法，检测关键点的位置。oFAST是带有方向的FAST角点检测算法，增加了计算角点方向，方向角为θ。

（2）将上述计算出来的BRIEF描述符定义为一个2N的矩阵，将矩阵旋转角度θ，就得到了有方向的BRIEF描述符，也就是Steered BRIEF描述符。

（3）用一种贪婪学习算法筛选具有高方差和高不相关的Steered BRIEF描述符，结果称之为rBRIEF。

所以，ORB特征描述符，实际上是oFAST和rBRIEF的组合计算所产生的。

ORB通常采用汉明距离匹配方法进行特征描述符的匹配，首先设定阈值M（最小值为零，最大值为特征描述符的长度），然后将2个进行匹配的特征描述符STR1、STR2按位进行异或操作，并计算所得结果STR3中的1的数量存于整型变量SUM中，如果SUM小于等于阈值M的值，则将此对特征进行匹配，否则不进行匹配。

通过ORB特征描述符的生成过程可以看出，ORB比较明显的缺点有两点：

（1）ORB特征描述符是通过随机选择特征点为中心，半径为r的邻域圆内的几组点对比较大小，并按位记录结果，所以当图像出现尺度变化时，对应的邻域也会发生变化，导致特征描述符发生变化，从而导致失配。

（2）ORB特征描述符本身不具备邻域的位置和空间信息，它只能描述以特征点为圆心，半径为r的邻域圆的像素信息，如果图像内部出现较多相似区域，会导致相似区域内的特征点其邻域内的像素信息基本一致。这时如果使用汉明距离匹配算法进行匹配，结果会因为相似区域无法分辨而出现较多的误匹配。

2 改进的ORB算法

汉明距离的单一方法会导致较高误差的匹配率。为了保证匹配率以及匹配精度，本文提出汉明距离和余弦相似度相结合的方法，改进ORB算法，即用Hamming距离反映向量在数值特征上的差异，用余弦相似性反映向量在方向特征上的差异，再进行特征点匹配，然后采用RANSAC方法消除误匹配来提高匹配性能。

余弦相似度是用余弦值来度量向量空间中两个向量之间的差异大小，与距离度量相比，余弦相似度更关注两个向量在方向上的差异，而不是距离或长度上的差异。余弦相似性是最常用的相似函数之一，其计算公式[22]如公式（4）所示：

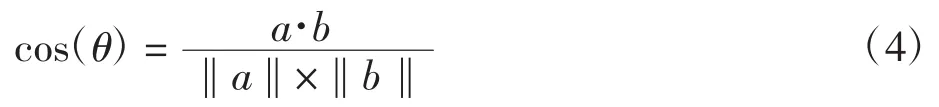
式中：a，b为要求取余弦相似度的 2个向量；cos（θ）为2个向量的余弦相似度；向量余弦的范围为[-1，1]。余弦值越大，表示2个向量之间的角度越小；余弦值越小，则2个向量之间的角度越大。

余弦可以用来评估几何中2个矢量之间的方向差。本文采用这一原理来度量特征向量之间的差异。改进ORB算法步骤如下：

（1）首先通过原始ORB算法用Hamming距离进行一次汉明距离阈值为P的特征点匹配，然后抽取其中N组特征点对，计算每组中2个特征向量之间的余弦相似度，记为数组C。

（2）将这N组点对的余弦相似度C两两作差，得到所有特征向量的余弦相似度之差存于数组A，之后将A数组内的数值两两作差，找出A数组中出现频率最高的一组数，将其余弦相似度赋值给θ，作为本次匹配过程的最优余弦相似度。简单的讲，θ是最接近这次匹配中，图像发生变化的角度B所计算的余弦值的值cos（B）。

（3）根据实验经验，考虑实际情况中机器误差等其他外界因素。用[θ-0.3，θ+0.3]作为阈值范围。

（4）应用Hamming距离特征匹配方法重新对图像进行自由度为m的特征点匹配（若阈值为P，则Hamming距离为[0，P+m]的均可先视为正确匹配），计算所有特征点对的余弦相似度存于数组D，如果余弦相似度在经验阈值范围内，则先视为正确匹配，若不在，则视为误匹配剔除。

（5）筛选后若仍然存在一个特征点有N组匹配都在阈值范围内的情况，则利用公式（5）进行筛选。

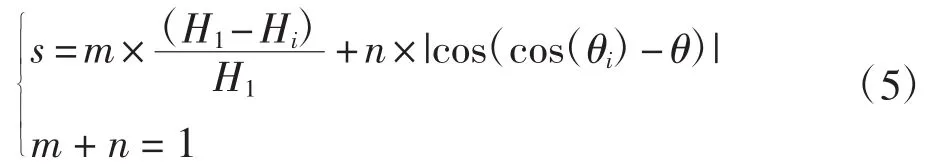
式中：Hi为第i个特征点与正在进行筛选的特征点之间的Hamming距离；H1为第1个特征点的二进制描述符的长度；cos（θi）为第i个特征向量与正在进行筛选的特征向量之间的余弦相似度；θ为最优余弦相似度；s为匹配相似度；m和n分别为距离权重和余弦相似度权重，代表二者在匹配过程中的重要程度。

（6）将N组匹配一次进行计算，保留s取得最大值的匹配视为最优匹配，其他的N-1个匹配消除。若N组的余弦角值都不在阈值范围内，则视为误匹配消除。

（7）应用RANSAC算法消除误匹配。

改进ORB算法流程图如图1所示。

改进ORB算法降低了距离相似度在特征匹配中的权重，重视图像之间存在的空间角度变化，该方法是以空间角度变化这一大方向为主导来进行特征点的匹配工作。

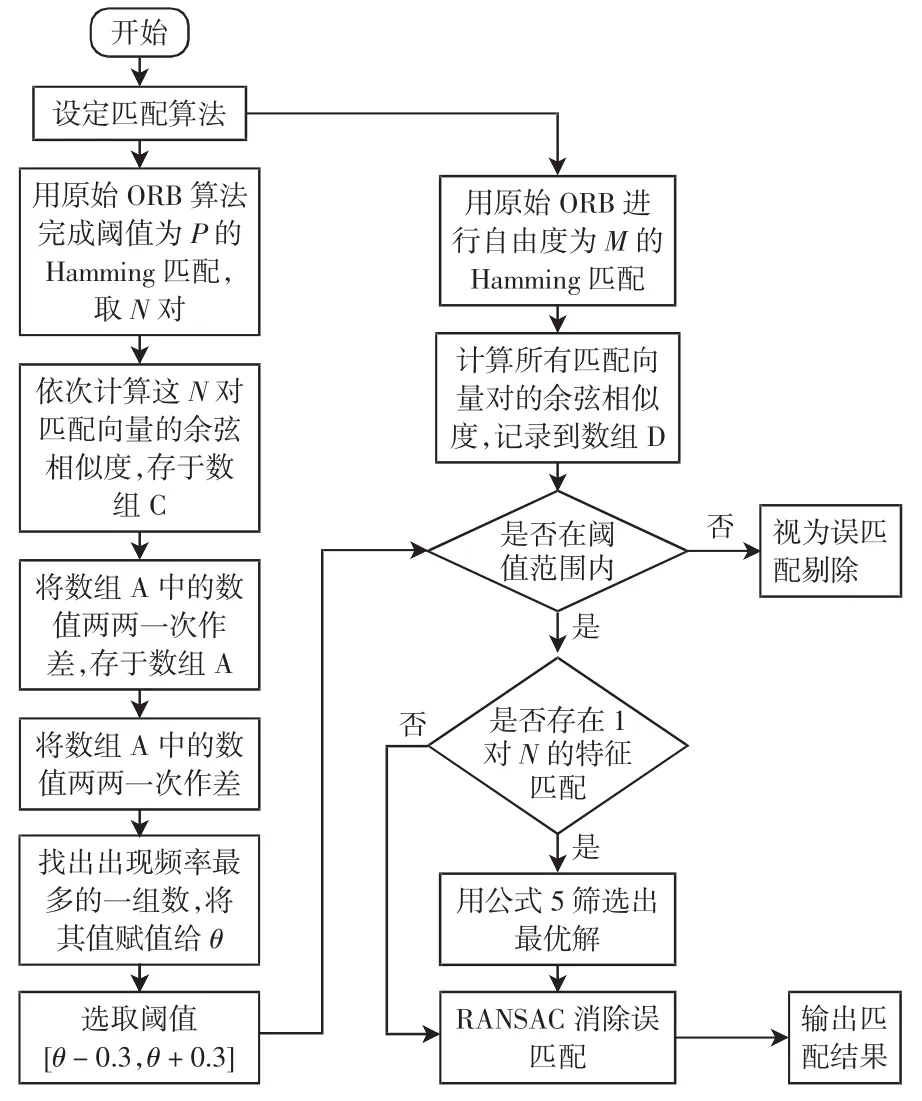
图1 改进ORB算法的流程图Fig.1 Flowchart for improving the ORB algorithm

3 改进ORB算法图像匹配实验

选择3组图片分别用原始ORB算法与改进后的ORB算法进行特征点匹配实验，并将结果用RANSAC算法消除误匹配。此实验应用系统环境是WIN7系统，CPU处理频率为3.7 GHz，软件使用的是VS2013软件，3组实验中图像匹配的参数设定如表1所示。

表1 3组实验图像匹配参数表Tab.1 Three groups of experimental images matching parameter table

改进ORB算法的参数设定如表2所示。

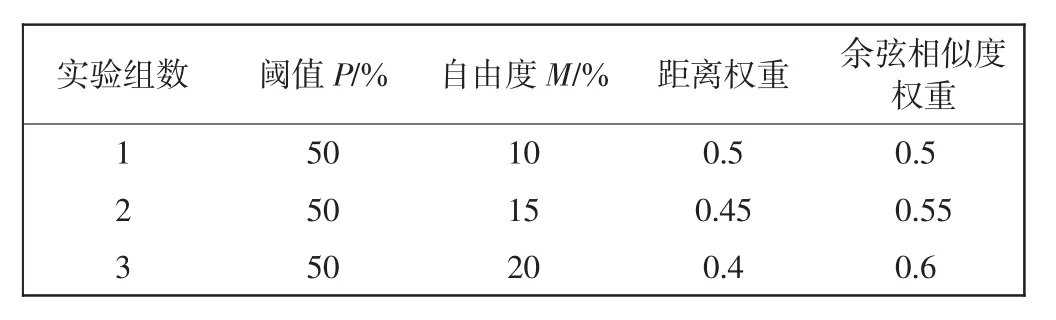
表2 改进ORB算法参数设定表Tab.2 Parameter setting for improving the ORB algorithm

3组图片匹配后的结果如图2所示。

图2 3组实验结果图Fig.2 Three groups of experimental results

从图2的3个图片的原始ORB算法与改进ORB算法匹配结果看，改进后的算法的特征点对多于原始算法，降低了RANSAC剔除误匹配后的特征，保持了匹配精度。实验结果数据对比如表3所示。

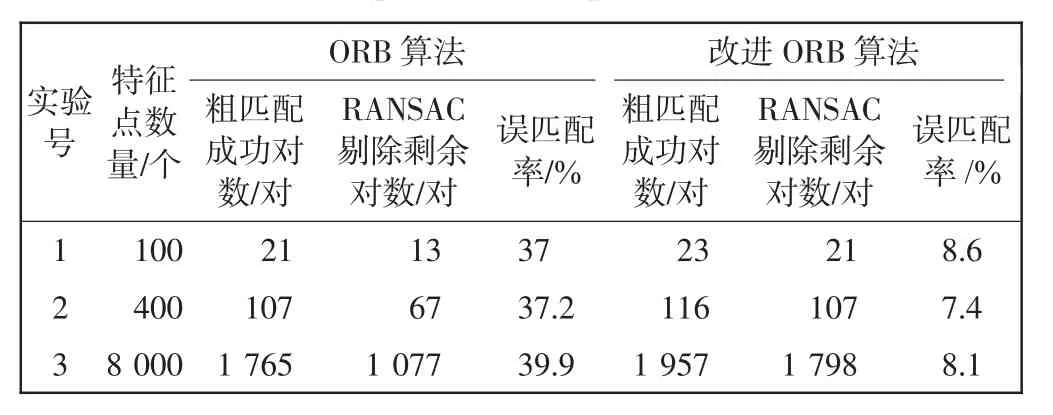
表3 综合实验结果Tab.3 Comprehensive experimental results

由表3可知，在第1组实验中，改进ORB算法的粗匹配成功率较原ORB算法提高了2%，误匹配率下降了28.4%；第2组实验中粗匹配成功率较原ORB算法提高了2.25%，误匹配率下降了29.8%；第3组实验中粗匹配成功率较原ORB算法提高了2.55%，误匹配率下降了31.8%。改进算法误匹配率仅为原算法的20%左右，降低了原算法误匹配率近80%。

上述3组实验证明了改进ORB算法在降低误匹配率上的可行性。而其中粗匹配率提高是因为降低了对汉明距离的阈值要求，更加注重两个特征向量的余弦相似度的相似性，使得有些原本应该被距离相似度剔除掉的特征点又有了成功匹配的机会。

4 改进ORB算法的对比分析

对一张拥有相似内部区域的图片进行尺度、旋转、平移变化，将变化后的图片与原图片分别用SIFT、SURF、ORB及改进的ORB算法进行特征点匹配实验，分析改进后的ORB算法的鲁棒性。匹配结果对比如图3所示，匹配结果数据统计分析如表4所示。

图3 4种算法匹配结果图Fig.3 Matching results of four algorithms

从图3和表4可以看出，SIFT算法获得最多的匹配点，但是时间耗时最久；SURF算法在效率方面是SIFT的近4倍；ORB算法特征点数量最少，但匹配速度却是SIFT的20多倍。本文提出的改进ORB算法，通过余弦相似度进行匹配，在抗旋转性能上效果显著，是原算法匹配点对数的2.39倍，匹配精度明显提高，而且匹配耗时相对较少。

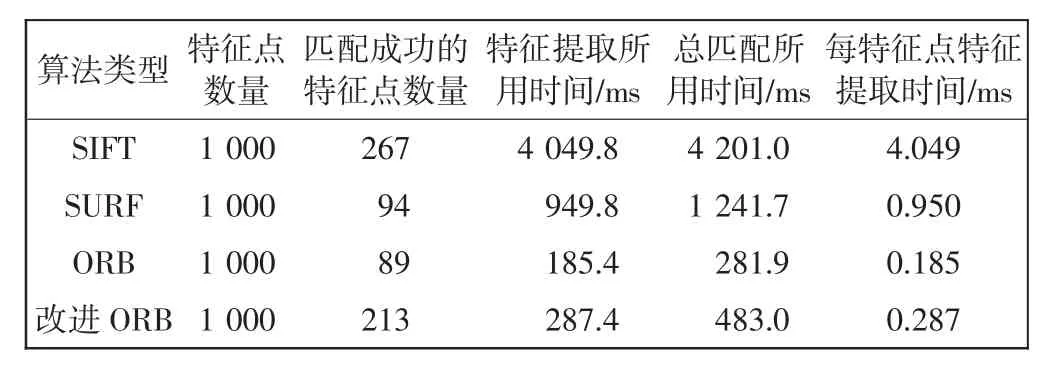
表4 4种算法匹配结果数据统计分析表Tab.4 Statistical analysis table of matching results of four algorithms

通过上述对比实验可以证明，本文提出的改进ORB算法，通过加入余弦相似度匹配与汉明距离匹配相结合，将图像存在多区域时原ORB算法的误匹配率降低，且随着匹配特征点数目的增加，降低的百分比也会随之增加。

5 标准数据集实验及分析

上述实验证明了本文改进的ORB算法相较于原ORB算法在多相似区域图像特征点匹配问题上误匹配率有明显的下降。本章节将原始ORB算法、本文改进的ORB算法、文献[15]提及的NN方法、文献[18]提及的融合描述子法在Mikolajczyk 05标准数据集中，通过视角变化（wall）、光照变化（leuven）、尺度和旋转变化（bark）、图像模糊（bikes）这4种图像变化，分析对比算法的性能。图4给出了4种变化的测试图像，每组图像都进行了不同强度的变化。

本实验通过改进最近邻匹配阈值K，重复10次匹配，并画出各算法错误率（1-precision）-查全率（recall）对比曲线。该曲线是图像匹配算法的常用评价指标，其中查全率是正确匹配点数与图像间一致区域数目比值，错误率是误匹配点数与总匹配点数的比值，在查全率相同时，错误率越小匹配效果越好，在错误率相同的情况下，查全率越大越好。对于整体曲线，曲线位置越高效果越好。

查全率和错误率的计算方法如公式（6）与公式（7）所示：

正确匹配点数以及图像间区域一致的区域，可通过公式（8）[23]进行计算：

图4 4种变化的图像序列Fig.4 Four variations of the image sequence

其中：ua和ub是2个特征区域；A为单应区域，与单应矩阵H对应；ε0为区域的交叠误差，实验中取20%。

实验结果如图5所示。

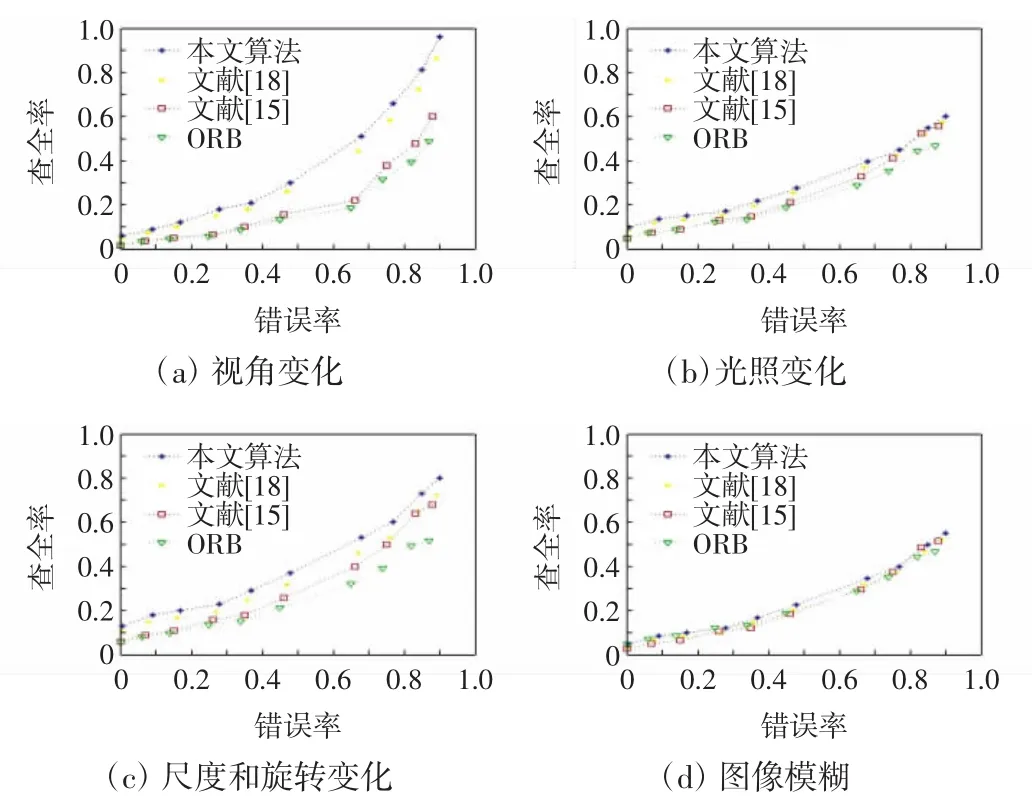
图5 错误率（1-precision）-查全率（recall）曲线Fig.5 Error rate(1-precision)-recall curve

根据实验结果分析，视角变化下，本文改进算法曲线位置相较于其他算法更高。由于视角变化图像序列的纹理结构有很强的局部相似性，因此也证明了本文改进算法在处理多相似区域图像特征点匹配时能力更为出色；尺度和旋转变化下，本文改进算法也表现出了超过其他3种算法的能力。而光照变化和图像模糊变化下，4种算法的性能基本相同，本文改进算法只是稍有优势。

6 结论

本文提出了一种改进ORB算法，将汉明距离相似性度量与余弦相似性度量相结合，首先通过汉明距离低自由度粗匹配，计算特征向量的余弦相似度，其次通过梯度计算法计算余弦相似度的最优阈值范围，然后在汉明距离高自由度粗匹配的基础上，利用余弦相似度不变性剔除误匹配点，最后用RANSAC算法再次精确匹配，解决了原ORB算法在匹配多相似区域图像时误匹配率高的问题。实验表明，该算法降低了原算法相似区域失配率80%左右。并且超越了ORB算法原有的对于图像变化的适应性（包括图像尺度变化、旋转变化、视角变化、图像模糊、光照变化），同时仍然保持着其运算的实时性。