等距变距混合曲线编程在数控加工中的应用

王永军，张青才

山西平阳重工机械有限责任公司 山西侯马 043000

1 序言

某零件如图1所示，其内腔曲线以基准轮廓线标注。内腔曲线为相对基准曲线呈等距变距混合分布的曲线。现有CAM图形软件对于如图1所示的零件，只能用如下公式生成基准轮廓线的样条图形。

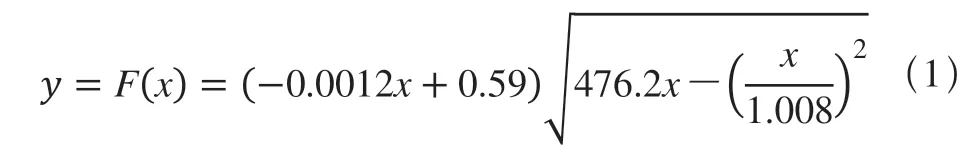
但由于内腔轮廓图形无法直接绘出，所以需借助专门的算法语言进行编程。本文针对类似混合等距变距曲线编程，给出了将距离引入参数方程及复合导函数表达变距曲线的数学建模法，并在程序计算中采用导数简化计算公式，解决了等距变距混合分布曲线的编程难题。

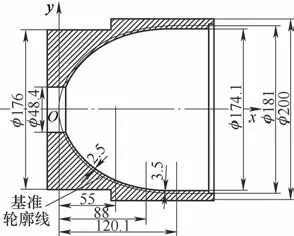
图1 零件示意

2 数学建模

图1中曲线建模示意如图2所示，F（x）为基准曲线，G（x）为等距变距混合曲线，r（x）为距离参数。G（x）的自变量方程用X表示。

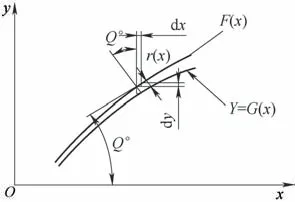
图2 曲线建模示意

设P（X，Y）为等距变距混合曲线上一点，则等距变距混合曲线Y参数方程，即基准曲线F（x）与变距曲线G（x）、距离参数R（x）间关系函数为：

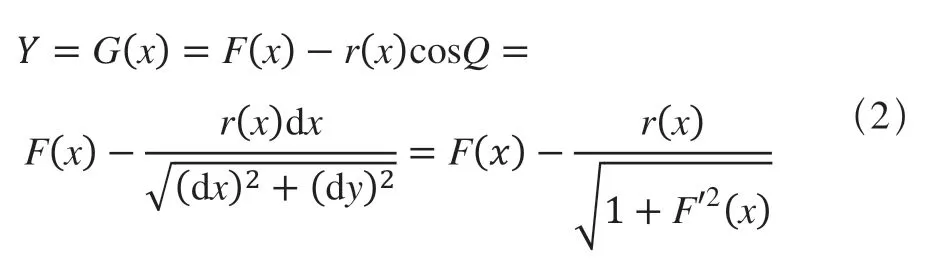
等距变距混合曲线自变量X参数方程为：

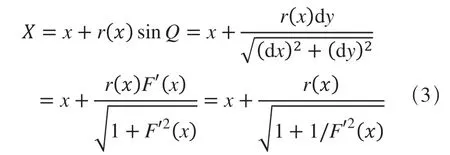
基准曲线与等距变距混合曲线间距离函数为：

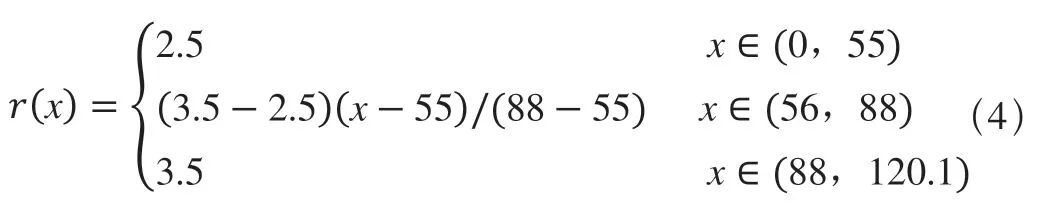
因F（x）式子复杂，其导数F'（x）公式计算困难，利用微分近似计算法，F'（x）采用如下公式计算：

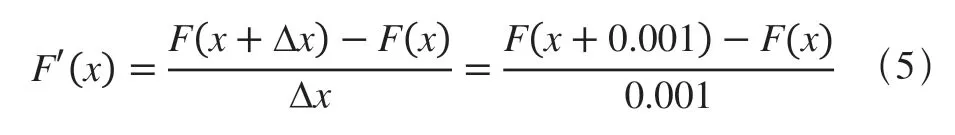
采用该公式在用算法语言求导计算编程时，编程更为简洁。

3 程序编制

3.1 算法语言程序编制

利用式2～式5，结合适当算法语言可以编制出图1中等距变距混合曲线的点位求解算法程序。以下为用QBASIC语言编制的算法程序。

a = .001

P = 0

DEF fnquy (x) = (-.0012 * x + .5808) * SQR(476.2 * x -(x * x) / (1.008 * 1.008))；（定义基准曲线函数）

DEF fndao (x, a) = (fnquy(x + a) - fnquy(x)) / a；（定义基准曲线导函数简化算式）

FOR Q = 0 TO 121 STEP .1；（重复计算点位）

x = Q

P = P + 1

IF x <= 55 THEN r = 2.5 ELSE IF x <= 88 THEN r = (3.5 -2.5) * (x - 55) / 33 + 2.5 ELSE r = 3.5；（距离函数赋值）

quxdao = x + r * fndao(x, a) / SQR(1 + fndao(x, a) ^ 2)；（计算等距变距混合曲线X自变量值）

quydao = fnquy(x) - r / SQR(1 + fndao(x, a) ^ 2)；（计算等距变距混合曲线Y值）

X1 = Q

y1 = fnquy(Q)

x2 = quxdao

y2 = quydao

OPEN “e:quxian.dat” FOR APPEND AS #1；（建立基准曲线点位文件）

WRITE #1, X1, y1, 0；（输出基准曲线点位到文件）

CLOSE #1

OPEN “e:pianxian.dat” FOR APPEND AS #2；（建立等距变距混合曲线点位文件）

WRITE #2, x2, y2, 0；（输出等距变距混合曲线点位）

CLOSE #2

NEXT

OPEN “e:quxian.dat” FOR APPEND AS #1

WRITE #1, P, 0

CLOSE #1

OPEN “e:pianxian.dat” FOR APPEND AS #2

WRITE #2, P, 0

CLOSE #2

END

3.2 程序结果图形检查

利用以上程序生成基准曲线的点位文件quxian.dat及等距变距混合曲线的点位文件pianxian.dat，将其导入CAXA电子图板，生成样条曲线如图3所示。

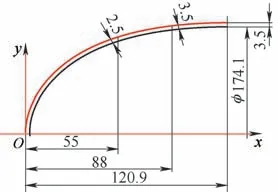
图3 样条曲线

经在CAXA电子图板下1∶1尺寸标注检查，生成的图样曲线完全符合图1要求，表明建模及算法程序是正确的。

利用生成的图形导出I G S文件，可导入任何CAM软件，编制图1零件的曲线车削数控程序，在此不再详述。

4 结束语

工程图样中以基准曲线为基准标注的等距变距混合距离的曲线，只要其等距及变距可以用式4类似的函数表达，且基准曲线可导，则利用式2及式3的推导方法，即可得出等距变距混合曲线函数的Y及X表达式。需要注意的是，式2及式3中的“＋”与“－”，应根椐零件图样的曲线凸凹及偏移方向结合而定，而非固定。同时，结合式4的简化求导计算式，即可编制出等距变距混合距离曲线的算法程序，进一步求出点位文件，并结合绘图软件及CAM软件，较为方便地编制零件数控加工程序。