基于ESP透视投影的FPS自动瞄准原理应用研究

◆唐逸帆 王皓宇 张仕斌

基于ESP透视投影的FPS自动瞄准原理应用研究

◆唐逸帆 王皓宇 张仕斌

（成都信息工程大学网络空间安全学院 四川 610103）

AimBot向来是FPS游戏安全最大的威胁，破坏了竞技的公平性与游戏程序的完整性，对游戏产业造成了巨大的经济损失，是安全人员不容忽视的问题，需要不断改进与完善游戏安全方案，为用户营造一个安全、公平的游戏环境。结合计算机图形学中的投影转换知识与在Unity3D中的具体实现，对FPS游戏中自动瞄准原理进行了简要论述与分析。

FPS游戏安全；计算机图形学；透视投影；Anti-cheat

自从1993年的FPS神作——毁灭战士发行以来至今，FPS（第一人称射击）游戏的热度从未衰减。随着网络游戏的飞速发展，FPS多人在线游戏的代表——绝地求生、Apex等大逃杀类游戏在吸引到越来越多玩家。由于FPS游戏的安全性问题，这类游戏也受到了黑色产业的“青睐”，Extra Sensual Perception（简称ESP，意为透视）与AimBot（自动瞄准）便是这其中的产物。

ESP和AimBot两种功能从实现细节上有很大差别，前者是3D坐标与2D坐标的变换问题，后者只涉及简单的角度计算。当然，这些知识对于游戏相关专业的同学来说，应该早已驾轻就熟了，笔者就不费太多篇幅来论述了。本文完全以初等数学的知识为基础，向读者阐述ESP和AimBot的原理。

1 AimBot（自动瞄准）原理及实现

AimBot，通俗来讲，就是使发射器（通常为枪械）精确地瞄准要射击的目标（通常为人类，载具等可攻击对象）。即，使弹道穿过要射击的目标（在忽略重力等因素的理想情况下）。

所以，要使发射器精确地瞄准要射击的目标，就需要修改游戏内存中的弹道数据。

要达到目的，需要解决两个问题：

（1）弹道在游戏内存中的表现形式是怎样的？

（2）如何计算正确的弹道？

2 FPS射击弹道的表现形式

弹道，即子弹飞行的轨迹，在早期的FPS游戏中弹道就是一条直线。但是，在一些追求真实感的军事模拟游戏中，弹道受到重力影响从而由直线变成弧线。在目前大多数网游FPS中，弹道仍然是一条直线。

在一些经典的游戏引擎中，如Source引擎，用欧拉角（Euler Angles）来表示弹道。许多新一代游戏引擎，如Unity，用四元数（Quarternion）来表示弹道。在某些游戏公司自主研发的游戏引擎中，弹道用弧度或向量来表示。

欧拉角和四元数在游戏中是用来表示角度或向量等信息，四元数可以通过欧拉角计算而得。四元数弥补了欧拉角的局限性，解决万向节死锁（Gimbal Lock）的问题。相比四元数，欧拉角在表示和运算上更为直观。

3 计算正确的弹道

观察图1，假设这样一个场景，你将要使用一把7.62mm口径的AKM自动步枪去射击一个僵尸，蓝色箭头Z代表AKM的弹道。

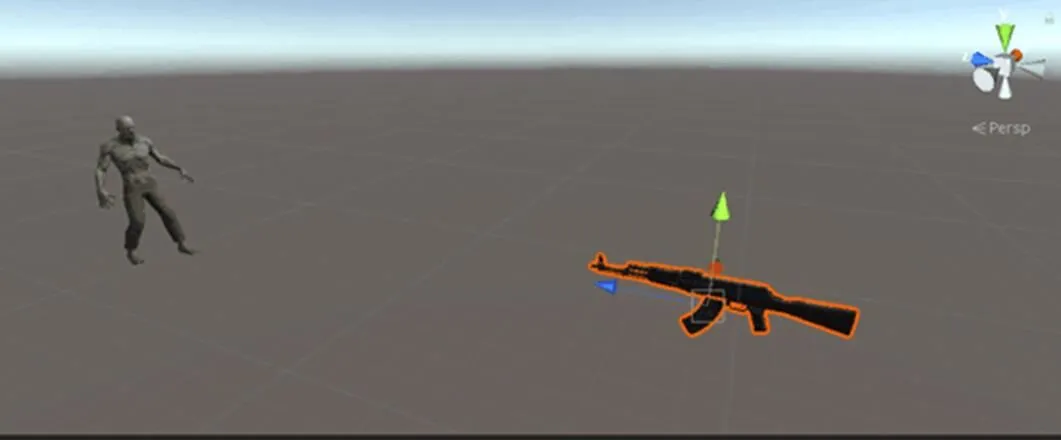
图1 射击场景图

假设AKM的位置固定，忽略重力等因素，要使AKM的弹道穿过僵尸，需要以下两个步骤：

（1）调整AKM在水平面XOY上的角度。

（2）调整AKM在垂直平面ZOX上的角度。

（备注：步骤的先后会影响四元数的表示）

图2 初始水平弹道（俯视图）

图3 调整后的水平弹道

图4 初始垂直弹道

图5 调整后的垂直弹道

在AKM和僵尸的坐标已知的情况下，很容易计算出弹道的欧拉角，将计算出的欧拉角写入游戏内存的对应位置即可。四元数也可以由相应的欧拉角计算而得。

欧拉角的计算过程属于初等数学的知识，在这里不再赘述。

4 Extra Sensual Perception（透视）原理及实现

4.1 游戏世界的表现形式

Extra Sensual Perception——ESP目前有两种主流的实现方式：

（1）禁用Z-buffer缓冲；

（2）透视投影的相关应用。

第一种方法容易被检测，透视效果不够灵活，目前第二种实现方式是主流，对FPS游戏威胁较大。ESP的功能是标识游戏中对象（敌人、物资），让使用者可以轻易发现掩体后的敌人或者物资。

计算机中的游戏场景以三维立体的形式进行渲染、存储等操作。但是，这样一个三维的场景却是通过电脑显示屏，以平面（就像一块布，一张照片）的形式展示出来。我们仅仅是通过一块平面来理解计算机中的立体游戏场景，就像是透过一个窗户，来观测另一侧的世界，这个窗户，就是FPS游戏中的相机。

具体来说，ESP是在2D屏幕标识游戏场景中的一个或多个3D坐标，比如笔者在2D的图片上标识了僵尸的位置。这就涉及3D坐标到2D坐标的转换。

图6 僵尸标记位置

计算机显示屏用2D坐标（XY）来表示一个点，而FPS游戏中的点是用3D坐标（XYZ）来表示一个点的。那么要实现ESP功能，我们就产生了第一个问题：如何将3D的坐标表示为2D坐标？

3D的坐标到2D坐标的变换过程需要许多复杂严谨的推导，为了减少篇幅，下面的论述剔除了一些非重点细节，省略了一些学术性的推理步骤，用相对简单的方法阐述ESP的原理与实现。

4.2 透视投影——3D坐标到2D坐标的转换

如何将计算机中3D的坐标表示为2D坐标？我们将这一个问题实例化一下。

假设，你正在透过窗户观测僵尸，并试图在窗户的玻璃上用笔勾勒出僵尸的肖像。注意，你的眼睛与窗户的相对位置不能改变，因为你可不想因为视角改变而重新画一遍。僵尸在现实世界中的坐标是3D的，它的肖像以2D的形式被你画在了玻璃上，这就是3D坐标到2D坐标的转换。肖像绘制的过程就叫作透视投影，玻璃上的僵尸肖像就是投影。

随后，将画有僵尸肖像的玻璃拆了下来，放进打印机里进行1:1扫描并上传到你的PC，打算作为电脑壁纸。但是，你发现肖像的大小和位置都不尽如人意，于是通过拉伸调整到了一个合适的大小。原本存在于现实世界中的僵尸肖像，通过无数个像素点呈现在了屏幕上，这便是光栅化。

在这个过程中，你的眼睛就可以称为FPS相机。至此，一个简单的ESP实现完毕。

4.3 用简单的数学来推导透视投影变换

目前我们只涉及了两个步骤，透视投影和光栅化。但是，FPS相机的完整投影还需要进行裁剪、转换到NDC坐标、将世界坐标转换为相机坐标等操作。裁剪就是把视野以外的物体排除掉，减轻计算机的渲染负担，但是实现ESP功能不需要进行太多渲染，可以忽略掉裁剪操作；NDC坐标的转换也是为了方便裁剪和计算屏幕坐标，裁剪操作可以忽略，屏幕坐标可以通过比例关系得到；将世界坐标转换为相机坐标，即将所有运算转换为以相机为坐标系原点来简化运算，这一操作很重要，但是相关矩阵构建过程并不复杂。

我们已经可以通过感官经验大致判断出僵尸最终在屏幕上的位置，但是，为了实现ESP我们需要更精确坐标。我们需要通过数学来计算一个精确的坐标。

计算步骤：

（1）利用相似三角形原理，计算出僵尸身上其中一个点的坐标中Xe投影到窗户上的Xp，计算Yp同理。

回到给僵尸画肖像的例子：

假设僵尸的鼻子坐标为（Xe，Ye，Ze），下标e代表Eye Space，即所看到的最直观最原始视觉空间。我们透过窗户玻璃用AKM瞄准僵尸（假设AKM上有用来辅助瞄准的红点激光），然后在激光与玻璃平面交汇地方上画一个点，这个点就是（Xp，Yp，Zp），下标p代表Project，即投影。此时玻璃相当于一个投影平面。

图7 屏幕投影坐标

设AKM为原点（0，0，0）建立坐标系，注意，轴正方向与红点发射的方向相反。我们此时建立的是右手坐标系。

先看俯视图：

图8 俯视图

图中=-的地方就是窗口的位置，称为近裁面（near plane）。=-的平面是远裁面，本文不作讨论。

根据相似三角形定理，求得：

同理可以得到：

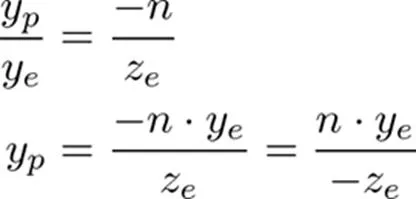
等于窗户轴坐标：=-=

得到最终结果：

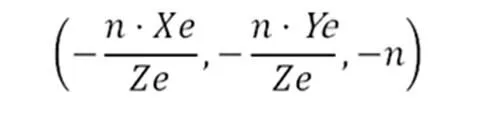
坐标是没有作用的，因为我们只求X，Y映射到游戏窗口上的像素坐标。

（2）测量窗户的实际高宽，通过比例关系得出X，Y在电脑屏幕上的像素坐标X，Y。

窗户的长宽是由你与窗户的距离还有视场角（Fov）决定。

Fov是一个角度，即站在窗户后面用AKM向外射击，所能达到水平方向上的极限。也可以说是你的视野的极限。垂直的极限可以由窗口高宽比推得，因为游戏窗口的分辨率和比例一般都可以在设置里面轻易取得。

图10 视场角

已知直角三角形的一边和一个角，即可通过三角函数求得所有的角和边。

最终得到窗户的宽：

窗户的高（Height）可以通过窗口比例（Aspect）求得。

接下来的运算就很简单了，通过窗户的实际高宽，可以很容易得到（Z，Y，-）像素坐标。

推导过程十分简单，就是通过简单的比例关系就可以求得像素坐标了。像素坐标是二维坐标系，假设游戏窗口大小为1024x768，在Unity里面是左上角为（0，0），右下角为（1024，768）。

最终公式：

（3）通过1、2步得到的线性变换，构造线性函数，带入僵尸身上所有的点，全部转换为像素坐标，即可在显示屏上得到完整图像。

5 代码

本文仅仅是构造一个简单的线性函数来描述3D到2D的投影变换，而游戏引擎中的投影运算往往要复杂得多，为了保证运算效率和封装性，往往要用到矩阵运算。矩阵可以说是多个线性运算的统一体，比如上面的ESP透视函数，也可以用一个矩阵来表示，也就是我们俗称的投影矩阵。

void LookAtEx（Vector3 CamPos， Vector3 Target）

{

Vector3 OrgZ = new Vector3（0， 0， 1）;

Vector3 LookV = Target - CamPos;

print（"LookV"+LookV）;

Vector3 tmp = LookV;

tmp.y = 0;

float Y = Vector3.Angle（OrgZ， tmp） * Mathf.Deg2Rad;

if （LookV.x < 0）

Y = -Y;

print（"Vector3.Angle（OrgZ， tmp）"+Y）;

float X = Vector3.Angle（tmp， LookV） * Mathf.Deg2Rad;

if （LookV.y > 0）

X = -X;

print（"Vector3.Angle（tmp， tmp2）" + X）;

print（"OrgZ"+OrgZ+"tmp"+tmp）;

// Y = aY*Mathf.Deg2Rad;

// X = aX*Mathf.Deg2Rad;

float Z = 0.0f;

float sinY， cosY， sinX， cosX;

Quaternion q;

sinY = Mathf.Sin（Y / 2）;

cosY = Mathf.Cos（Y / 2）;

sinX = Mathf.Sin（X / 2）;

cosX = Mathf.Cos（X / 2）;

q.w = cosX*cosY;

q.x = sinX*cosY;

q.y = cosX*sinY;

q.z = -sinX*sinY;

print（q.w）;

print（q.x）;

print（q.y）;

print（q.z）;

cam.transform.SetPositionAndRotation（cam.transform.position，q）;

float c1，c2，c3，s1，s2，s3;

s1 = Mathf.Sin（Y / 2）;

c1 = Mathf.Cos（Y / 2）;

s2 = Mathf.Sin（Z / 2）;

c2 = Mathf.Cos（Z / 2）;

s3 = Mathf.Sin（X / 2）;

c3 = Mathf.Cos（X / 2）;

q.w = c1 * c2 * c3 + s1 * s2 * s3;

q.x = s1 * s2 * c3 + c1 * c2 * s3;

q.y = s1 * c2 * c3 - c1 * s2 * s3;

q.z = c1 * s2 * c3 - s1 * c2 * s3;

}

void LookAt（Vector3 CamPos， Vector3 Target）

{

//Cam Org Forward

Vector3 OrgZ = new Vector3（0，0，1）;

//print（cam.transform.forward + "OrgZ"）;

//Cam to target

Vector3 LookV = Target - CamPos;

// print（LookV + "LookV"）;

//θ 点乘

float Cta = Vector3.Angle（OrgZ， LookV） * Mathf.Deg2Rad;

//print（Cta + "Cta" + Mathf.PI / 4）;

//n 叉乘

Vector3 n = Vector3.Cross（OrgZ， LookV）.normalized;

// print（n + "n"）;

//n =new Vector3（-5，0，0）;

//Cta = Mathf.PI/4;

Quaternion q = new Quaternion

{

w = Mathf.Cos（Cta / 2），

x = n.x * Mathf.Sin（Cta / 2），

y = n.y * Mathf.Sin（Cta / 2），

z = n.z * Mathf.Sin（Cta / 2）

};

cam.transform.SetPositionAndRotation（cam.transform.position，q）;

//print（cam.transform.forward + "forward"）;

}

6 结语

理想情况下，我们可以得到FPS相机坐标、FOV、敌人坐标、构建好的世界矩阵和投影矩阵，只需要调用几个Directx相关的API即可实现AimBot和ESP，当然，那只是理想情况。更多的情况下，我们需要解密游戏中加密的数据，通过矩阵的各种运算得出我们想要的数据，甚至需要构建游戏引擎不存在的矩阵并封装专门的函数。由此可见，理解ESP与AimBot的原理是十分重要的。

本文还有一个重要的知识点没有讨论，那就是相机矩阵（View Matrix），其作用是将世界坐标转换为以相机为原点的坐标。笔者认为相机矩阵的构建和推导比较简单，只需要用到一部分仿射变换和初中几何知识。

了解矩阵中每一行每一列的含义、构造方式以及矩阵在内存中的表现形式，在面对游戏中海量的数据时，才不会像大海捞针一般。

[1]许社教.三维图形系统中两种坐标系之间的坐标变换[J].西安电子科技大学学报，1996（03）：137-140.

[2]蒋亚军.世界场景中三维观察变换的实现[J].吉首大学学报（自然科学版），2006（05）：31-33.

[3]Fletcher Dunn，Ian Parberry. 3D Math Primer for Graphics and Game Development. 2015.

[4]백낙훈.Interactive Computer Graphics：A top-down approach with OpenGL. 1999，17（7）：69-71.

国家自然科学基金（62076042，61572086）；四川省重点研发计划项目（No. 2020YFG0307，No. 2018TJPT0012）；成都市重点研发计划项目（No. 2019-YF05-02028-GX）；四川省高校科研创新团队项目（No.17TD0009）；四川省学术和技术带头人培养支持经费资助项目（No. 2016120080102643）