电机-减速一体化壳体有限元分析

2021-02-27马银生冯圣国焦学健苏尚彬

农业装备与车辆工程 2021年2期

关键词：轴承座减速器壳体

马银生，冯圣国，焦学健，苏尚彬

（1.255049 山东省淄博市山东理工大学交通与车辆工程学院；2.266071 山东省青岛市青岛天赢智能工业股份有限公司；3.256414 山东省淄博市山东工业职业学院冶金与汽车工程系）

0 引言

随着社会经济的快速发展，世界范围内汽车保有量不断攀升，对石油的需求也在日益增加，由此引发的环境污染问题愈发严重。另外，石油等不可再生资源日益减少。在此背景下，新能源汽车因节能环保等优点获得迅速发展，纯电动汽车成为各国的研究热点。

纯电动汽车减速器是传动系统的重要部件，减速器壳体对支撑和保护壳体内部齿轮轴系起到重要作用。减速器壳体的强度会直接影响减速器的传动性能[1]，应有足够的强度才能保证汽车安全行驶，因此有必要对减速器壳体结构进行强度校核计算。

本文以纯电动汽车电机-减速一体化壳体为研究对象，应用有限元法对壳体的强度进行计算，通过力的平衡关系求解各个轴承座承受的载荷大小，建立壳体有限元模型，求解计算后得到壳体的应力及位移分布云图，并通过查看壳体的最大应力及最大位移来判断壳体是否满足强度和刚度要求。

1 壳体强度校核理论

电机-减速一体化壳体采用塑性材料铝合金，当壳体承受一定程度的载荷后将发生塑性屈服，常用第四强度理论，即畸变能密度理论（Von Mises 理论）作为壳体静力分析的强度准则。通过该理论可知，若结构上的某一部位的最大应力超过了结构材料的屈服极限，该点就会发生塑性屈服。通过式（1）计算畸变能密度：

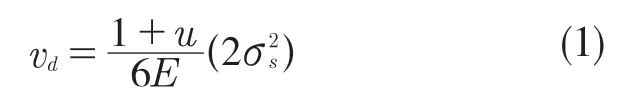
式中：vd——畸变能密度；u——材料的泊松比；E——材料的弹性模量；σs——材料的屈服强度。

通过式（2）对畸变能密度进行计算：

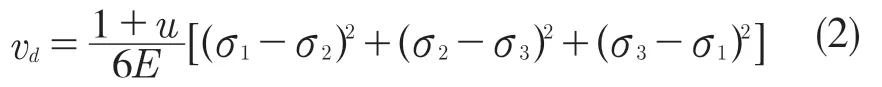
式中：σ1，σ2，σ3——单元的主应力。

由式（1）、式（2）可得屈服准则：

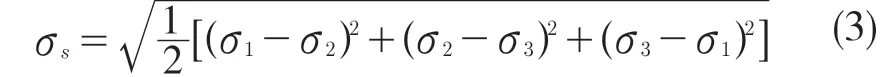
畸变能密度理论的强度应满足：

式中：σi——结构上某一点的应力；[σ]——许用应力，可通过式（5）求得：

式中：ns——选取的材料安全系数。

1.3疗效标准和评价标准参照《中医病症诊断疗效标准》,疗效标准:有效:治疗后症状和体征得到有效缓解甚至消失;无效:症状和体征无变化,腰痛情况持续存在或12个月内复发持续性疼痛。评价标准:VAS评定疼痛程度:0表示无痛;1-3分表示轻微疼痛,能忍受;4-6分表示疼痛已经困扰患者的生活,睡眠,但尚可忍受;7-10分表示无法忍受的疼痛。

由于电机-减速一体化壳体的结构比较复杂，并且在减速器工作过程中，壳体承受的载荷也比较复杂，因此不能使用传统的理论力学计算壳体的强度。本文应用有限元法对壳体强度进行计算求解，首先建立壳体有限元模型，然后对模型准确施加载荷及位移约束等边界条件，最后可通过分析后的应力云图得到壳体应力分布情况。

2 壳体结构及受力分析

2.1 壳体结构

电机-减速一体化壳体共由2 部分组成：前壳体及后壳体。前壳体与后壳体、后壳体与电机之间均采用螺纹连接，前壳体与后壳体上均设有轴承孔、加强筋及螺纹孔等结构。在前处理软件HyperMesh 中虽然有三维实体建模功能，但只能创建简单模型，并不能建立空间结构较复杂的模型。本文使用三维建模软件CATIA 建立的电机-减速一体化壳体几何模型如图1 所示。

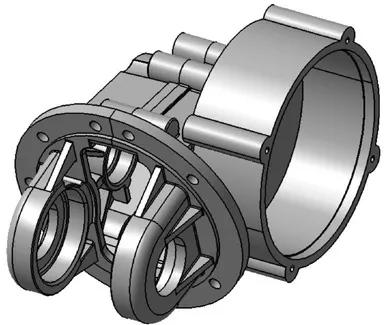
图1 电机-减速一体化壳体模型Fig.1 Motor-reducer integrated housing model

纯电动汽车减速器的传动原理如图2 所示。纯电动汽车以驱动电机作为动力输入的来源，电机轴与输入轴为一体轴，电机带动一体轴上的齿轮Z1 转动，齿轮Z1 与中间轴上的齿轮Z2 相啮合带动中间轴转动，然后中间轴上的齿轮Z3 与减速齿轮相啮合，最终带动半轴的转动，驱动汽车能够正常行驶。

图2 减速器传动原理图Fig.2 Schematic diagram of reducer drive

2.2 受力分析

由于减速器内部的齿轮、轴系及轴承等结构部件的重力对壳体的性能影响很小，所以在分析过程中忽略其重力的影响。

在对壳体进行静力分析前，需要先计算壳体所承受的载荷。减速器的传动系采用斜齿轮，斜齿轮在传动过程中啮合产生的轴向力Fa、径向力Fr以及周向力Ft通过齿轮轴传递给轴承，进而作用在壳体上，因此先计算各齿轮轴的受力情况，进而计算出壳体所承受的载荷。

斜齿轮间产生的啮合力可分解成沿齿轮的轴向力Fa、径向力Fr以及周向力Ft三个相互垂直的分力，各力的计算公式为[2]

式中：Ft——周向力；Td——齿轮传递的扭矩；d——齿轮分度圆直径；Fr——齿轮径向力；αn——齿轮法向压力角；β——齿轮分度圆螺旋角；Fa——齿轮轴向力。

建立峰值转矩工况下输入轴的受力分析简图如图3 所示。

轴的两端支撑点处的受力大小由力学平衡关系式（7）可得：

同样，根据力学平衡关系式可计算得到中间轴及差速器总成两端轴承支撑点的载荷大小，最终得到各轴承座所受支反力的大小。各个轴承座所承受的载荷如表1 所示。

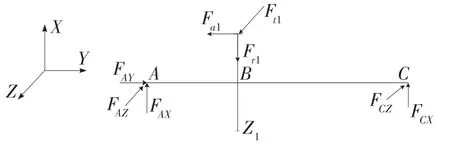
图3 输入轴受力分析简图Fig.3 Simple diagram of input shaft force analysis

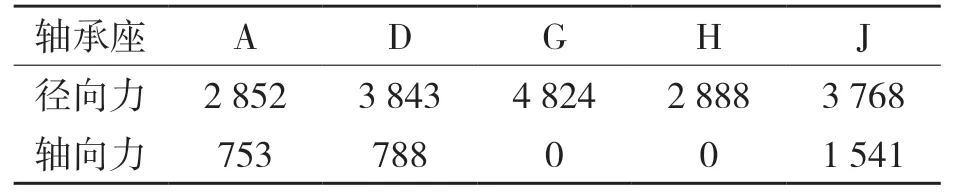
表1 各轴承座支反力载荷(N)Tab.1 Reaction force load of each bearing block (N)

通过上述对各个传动轴所受载荷大小的计算，得到各轴承座所承受的载荷，轴承座处承受一个径向合力FR和一个轴向力。径向合力作用在轴承上，通过轴承以分布压力载荷的形式作用在轴承座上，在以下分析过程中，作用于轴承座上的径向载荷按照余弦函数分布在以竖直方向为中心的两侧各60°范围内[3]。作用在轴承座上的余弦规律载荷分布如图4 所示。

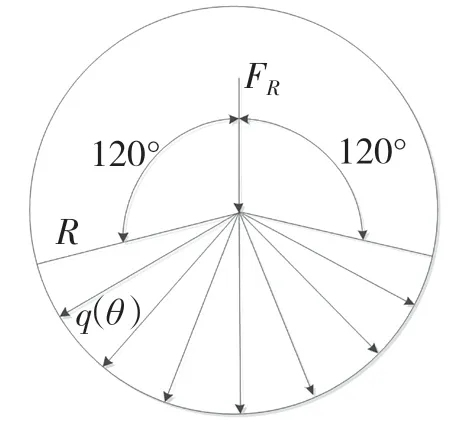
图4 轴承座径向压力载荷余弦函数分布Fig.4 Distribution of cosine function of radial pressure load of bearing block

图4 中：θ——弧度；FR——在轴承孔处施加的径向载荷；R——轴承孔处的圆弧半径。

假设在α 弧度范围内，在轴承孔宽度为W的圆弧范围上施加余弦载荷[3]。分布载荷公式为

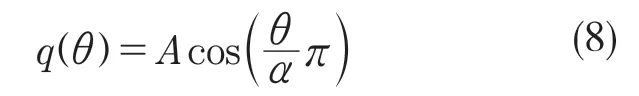
最后可得轴承孔余弦载荷分布形式为

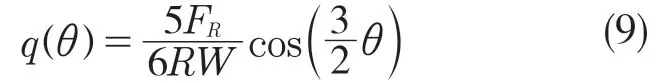
3 有限元建模

3.1 简化模型

在建立壳体的有限元模型时，应该简化对壳体强度影响较小的部位，如去除非关键部位的过渡圆角，只保留受力较大的轴承座附近的圆角特征，并去掉螺栓孔上的螺纹及倒角。

3.2 设置材料属性

电机-减速一体化壳体采用6061-T6 铝合金材料，其弹性模量为70 MPa，泊松比为0.33，密度为2 700 kg/m3，屈服强度为240 MPa[4]。

3.3 划分网格

由于电机-减速一体化壳体结构较复杂，六面体网格不容易划分，因此选用四面体进行划分网格。为得到比较精确的计算结果，本文选用二阶四面体CTETRA 单元对模型进行网格划分。单元尺寸确定为3 mm，对于承受较大载荷的轴承座及附近区域进行细网格的划分。检查网格的质量并改进不合格的单元，网格质量的良好与否将直接影响计算过程能否顺利完成，并且也会影响分析结果的精度[5]，因此在网格划分过程中必须检查网格的质量，通过改进网格质量使得所有网格符合长宽比（Aspect）、翘曲度（Warpage）、偏斜度（Skew）、雅克比（Jacobian）、内角等标准。本文检查标准如图5 所示。

图5 网格质量检查标准Fig.5 Grid quality inspection standard

4 边界条件

电机-减速一体化壳体通过法兰与驱动桥壳连接，后壳体与电机相连接。因此约束壳体上与驱动桥壳相连接的9 个螺栓孔的所有自由度，考虑到电机刚性较大，约束后壳体与电机连接部位的所有自由度。

在壳体轴承座位置施加分布载荷及相应位置施加位移约束后，最终的有限元模型如图6 所示。

图6 壳体有限元模型Fig.6 Shell finite element model

5 结果分析

应用OptiStruct 求解器对有限元模型分析计算，壳体的应力及位移云图分别如图7、图8 所示。

图7 壳体应力云图Fig.7 Shell stress cloud diagram

图8 壳体位移云图Fig.8 Shell displacement cloud diagram

由应力分布云图可知，壳体的最大应力为63.3 MPa，位于轴承座J 处。壳体其他区域的应力较小，均在35MPa 以下。

进行静力分析时，通常取塑性材料的安全系数为1.2～2.5[6]。本文是在电机峰值转矩下对壳体进行校核，取安全系数为1.5，通过材料许用应力计算公式可知许用应力[σ]=160 MPa。壳体上的最大应力值为63.3 MPa，小于材料的许用应力160 MPa，因此壳体在峰值转矩工况下满足强度要求，不会发生屈服失效。

从位移分布云图可以看出，壳体的最大位移为0.112 mm，根据QC/T 534-1999《汽车驱动桥台架试验评价指标》可知，驱动壳体的最大变形必须小于1.5 mm/m。本文中的减速器搭载的样车的轮距为1 360 mm，计算出壳体的最大变形为0.015 mm/m，满足性能要求。