基于自适应阈值的小波BP 神经网络风电变桨系统故障预测

肖 成， 刘作军， 张 磊

（1.河北工业大学 人工智能与数据科学学院， 天津 300130； 2.北华航天工业学院 电子与控制工程学院， 河北廊坊 065000）

0 引言

由于环境污染严重和相关政策的扶持，风电机组装机容量不断增大[1]。 由于风电机组长期运行在复杂多变的恶劣环境中，很容易造成风机故障，导致长时间停机[2]，[3]。 故障预测可以有效地提高机组运行的可靠性，及时发现异常状态，提前实 施 预 防 性 维 修[4]，[5]。

风电变桨系统是当今大型风电机组中重要的组成部分， 直接决定了机组吸收风能的大小。由于该系统的执行机构很容易产生一定的机械故障，造成变桨系统故障发生的频率很高。 BP 神经网络算法采用误差反传的方式，具有更加良好的非线性映射能力， 被广泛应用于故障诊断、故障预测等领域。 本文利用小波对提取的机械信号特征敏感的特点，将小波分析引入到风电机组变桨系统故障预测中。

小波变换方法和神经网络算法用于故障的识别和诊断已经取得了一些成果。 文献[6]以谱峭度作为指标求取信号时间-小波能量谱， 实现了滚动轴承早期微弱故障信号的特征提取。 文献[7]利用小波分解描述了风力发电机齿轮箱的故障信息，成功地进行了故障识别。 文献[8]研究了基于人工神经网络和离散小波变换的智能诊断方法。 文献[9]通过采用Apriori 关联规则和Relief F算法进行了故障特征选择， 并建立了BP 神经网络模型，验证了故障预测的可行性。

针对小波阈值处理函数中硬阈值会使重构信号在阈值区间内不连续， 而软阈值造成重构信号与真实信号存在一定误差的问题， 本文引入了一种自适应阈值的小波去噪方法， 并将自适应阈值的小波BP 神经网络算法应用于风电机组变桨系统的故障预测中。

1 自适应阈值的小波原理分析

1.1 小波分析

小波分析是一种有效的时域和频域分析方法，实现了在不同的尺度上观察信号[10]。

式中：a 为伸缩因子，决定了波动幅度；b 为平移因子，决定了波动时间。

任意信号f（t）∈L2（R）的连续小波变换为

从风力发电SCADA（监控与数据采集）系统采集到的数据多为离散数据，须要进行离散小波变换。 于是，将连续小波ψa，b（t）和连续小波变换Wf（a，b）离散化。 对应的离散小波函数表示为

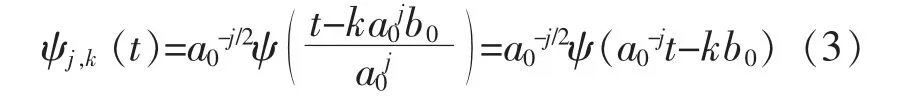
式中：j，k∈Z。

离散小波变换系数为

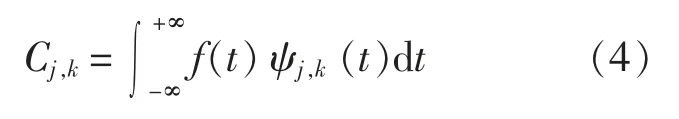
重构公式如下所示：

本文采用小波三层分解，如图1 所示。

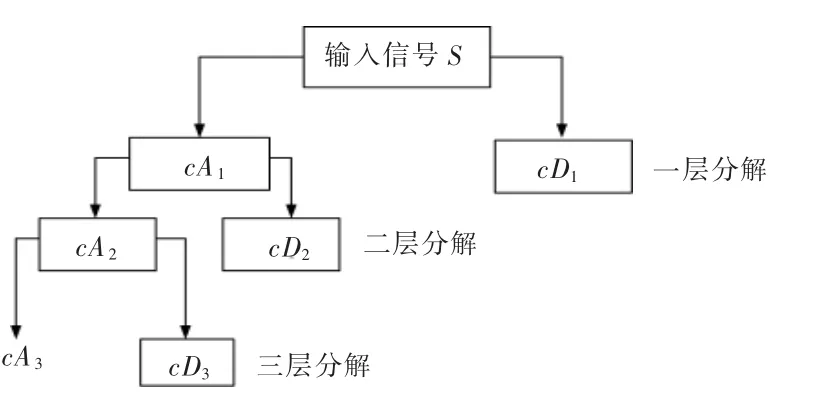
图1 小波三层分解图Fig.1 Wavelet three-layer decomposition graph

每进行一次小波分解，都把输入信号分解为高频和低频两个部分。 小波分解中cA 为低频近似系数，cD 为高频细节系数。 小波分解满足如下关系：

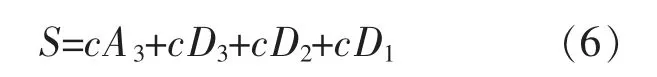
1.2 自适应阈值的小波去噪

小波阈值去噪法实现简单、计算量小，是目前应用最为广泛的一种滤波算法。 阈值函数实现了对模大于或小于设定阈值的小波系数处理，比较常见的有硬阈值函数和软阈值函数[11]。

硬阈值函数为

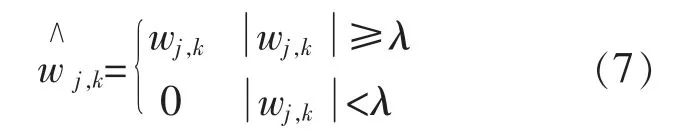
软阈值函数为

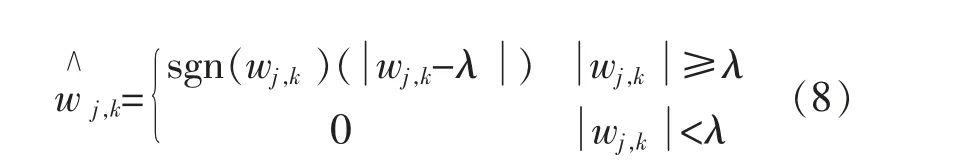
式中：wj，k为原始小波系数；λ 为阈值；为经阈值处理函数处理后得到的小波系数；sgn （·）为符号函数。

硬阈值在[-λ，λ]区间内不连续，则重构函数会出现振铃、伪吉布斯等现象；软阈值相比硬阈值在[-λ，λ]区间内是连续的，去噪效果较平滑，但是当模大于阈值λ 时，wj，k和w∧j，k总会存在恒定的偏差，造成重构信号与真实信号存在一定的误差。总体来说，软阈值处理效果优于硬阈值，后续采用软阈值方法作为对比算法。

为了合理地选取阈值函数， 本文通过构造一种介于硬阈值和软阈值之间的阈值函数， 实现调整软、硬阈值的程度。 该自适应阈值处理函数为

式中：mj为可变换取值。

mj可以取大于1 的连续实数，当mj=1 时，可变阈值函数非常接近软阈值函数；当mj＞10 时，该函数则非常接近于硬阈值函数。 自适应阈值处理函数通过自适应地调整mj得到不同尺度上小波系数适用的阈值函数，mj与小波分解尺度上的能量有关。

1.3 基于自适应阈值的小波去噪效果验证

以风速为例进行说明，先进行小波三层分解，分解成一个低频近似系数和三个高频细节系数。原始风速、 软阈值消噪和自适应阈值函数消噪后的风速如图2 所示。

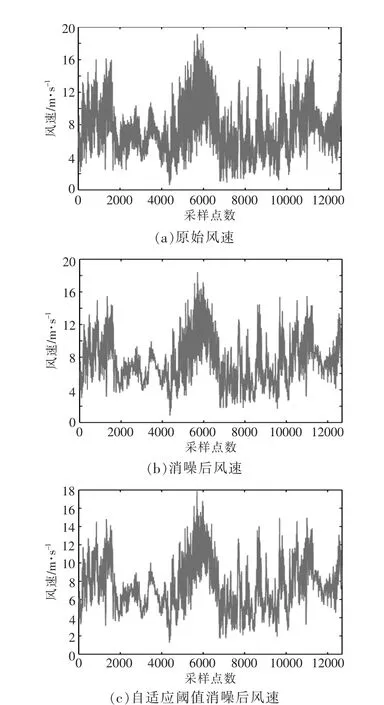
图2 风速对比图Fig.2 Wind compared chart

由图2 可知， 小波消噪可以有效地降低风速信号中的干扰量， 采用自适应阈值函数对小波消噪的效果最好。对风速、软阈值消噪和自适应阈值函数消噪后的风速低频、高频分量进行小波重构，结果如图3 所示。

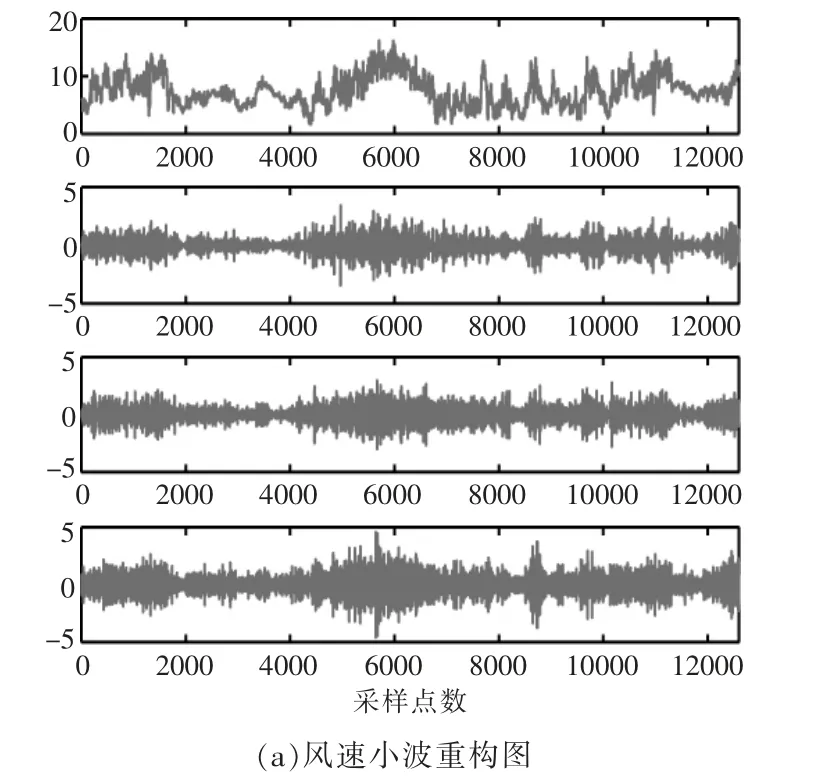
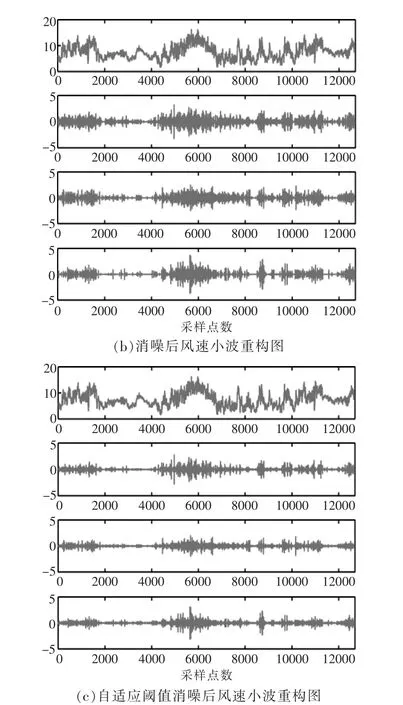
图3 风速小波重构图Fig.3 Wind wavelet reconstruction graph

由图3 可知， 经消噪后的风速低频和高频分量小波重构，受噪声干扰影响较小，且采用自适应阈值消噪后重构的效果优于软阈值消噪效果。

综上， 将风电SCADA 数据提取的故障特征经小波三层分解后， 对3 个高频细节系数cD1，cD2，cD3进行自适应阈值函数处理，实现了故障特征的小波消噪。

2 自适应阈值的小波BP 神经网络算法

2.1 BP 神经网络算法分析

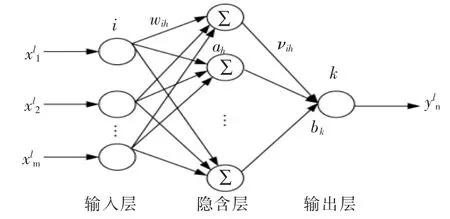
图4 三层BP 神经网络模型Fig.4 Three-level BP neural network model

BP 神经网络结构图如图4 所示。图中： Xl=（xl1，xi2，…，xlm）为输入变量；Yl=ynl为输出的期望变量；wih为输入层第i 个神经元和隐含层第h 个神经元之间的连接权值；νhk为隐含层第h 个神经元和输出层第k 个神经元之间的连接权值；ah为第h 个神经元的阈值；bk为输出层第k个神经元的阈值。

2.2 自适应阈值的小波BP 神经网络算法分析

本文采取嵌套式结合的方式，将小波分析融入到BP 神经网络中， 包括小波分析预处理模块和基于BP 神经网络的故障预测模块。

首先，将信号送入算法中，先进入预处理模块，实现对信号的离散小波分解，得到4 个小波系数：cA3，cD3，cD2和cD1。

其次，对高频细节系数进行自适应阈值函数处理，实现了系数消噪。

随后， 将处理好的系数送入到4 个BP 神经网络中，进行故障预测模型训练。

最后，对训练网络得到的输出信号小波重构，比较网络训练的重构信号和实际输出信号，进行故障预测结果分析。

自适应阈值的小波BP 神经网络故障预测模型结构如图5 所示。

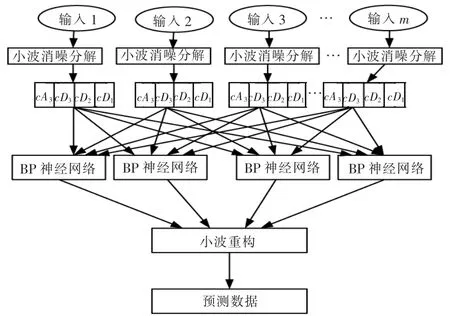
图5 自适应阈值小波消噪BP 神经网络预测模型结构Fig.5 Adaptive threshold wavelet denoising BP neural network prediction model

故障预测网络以桨距角、无功功率、电网频率、风向、风速和有功功率作为输入，转子位置作为输出。 因此，BP 神经网络输入层节点数为6、输出层节点数为1、隐含层节点数为13。

3 实验结果分析

3.1 实验数据构成

为了保证训练集和测试集的样本多样性，对于故障运行数据，分别提取变桨系统故障发生前15 d 的数据，每个故障时间段内采集数据100 组。提取的正常运行数据与故障数据相同。 提取到的每组数据中， 正常运行数据维数为18 100×7，故障运行数据维数为18 100×7。 其中，训练数据维数为12 600×7，测试数据维数为5 430×7。

3.2 性能评估指标

本节选取两类指标作为故障预测的性能评估指标，分别为性能指标和误差指标。

选取准确率（ACC）、精确率（Precision）、召回率（Recall）、诊断能力评价（Specificity）和可信率（Negative Prediction）作为性能指标。

式中：TP 为检测正确， 风电机组正常运行；FN 为检测错误，风电机组故障运行；FP 为检测错误，风电机组正常运行；TN 为检测正确， 风电机组故障运行。

以误差积分IE、绝对误差积分IAE 和平方误差积分ISE作为误差指标。

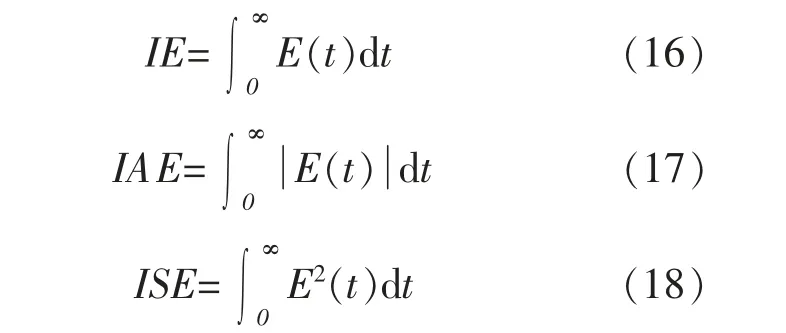
式中：E（t）为误差。

3.3 实验结果分析

（1）预测性能指标分析

比较故障预测的网络输出与实际输出， 得到故障预测结果如表1 所示。

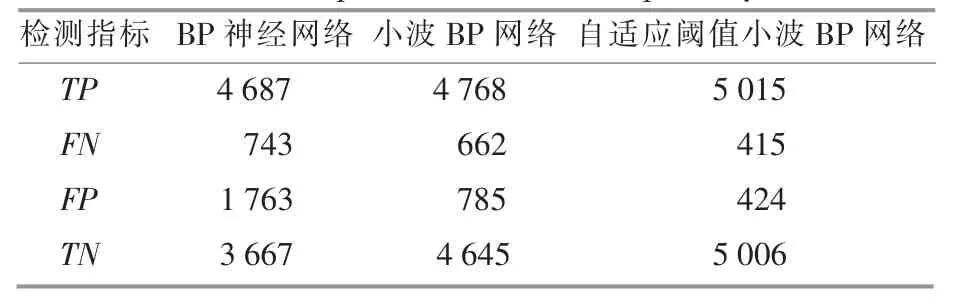
表1 变桨系统故障预测结果Table 1 Fault prediction results of pitch system

对比以上两种训练模型， 得到的故障预测性能指标如表2 所示。

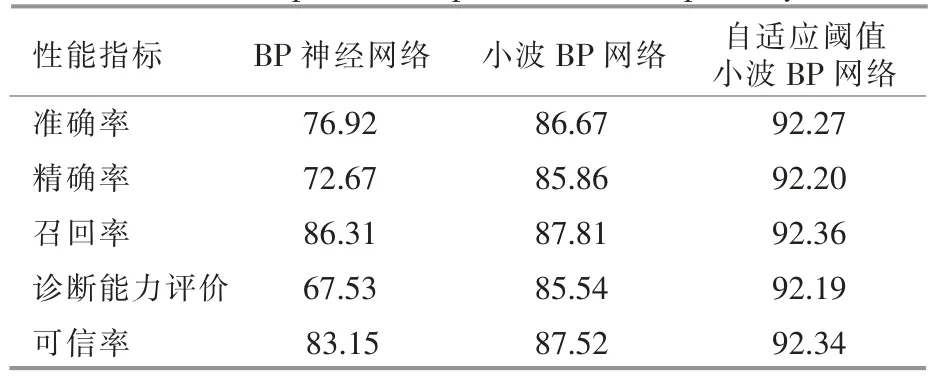
表2 变桨系统故障预测性能指标Table 2 Fault prediction performance of pitch system %

通过对预测结果和预测性能指标进行分析，发现自适应阈值的小波BP 神经网络预测效果优于小波BP 神经网络和BP 神经网络，准确率分别提高了5.6%和15.35%，而且在精确率、召回率、诊断能力评价和可信率方面均有显著提升。

（2）预测输出与实际输出

比较BP 神经网络和自适应阈值的小波BP神经网络算法的变桨系统故障预测网络输出与实际输出，结果如图6～9 所示。

图6 正常训练网络输出与实际输出Fig.6 Comparison of normal training network output with actual output

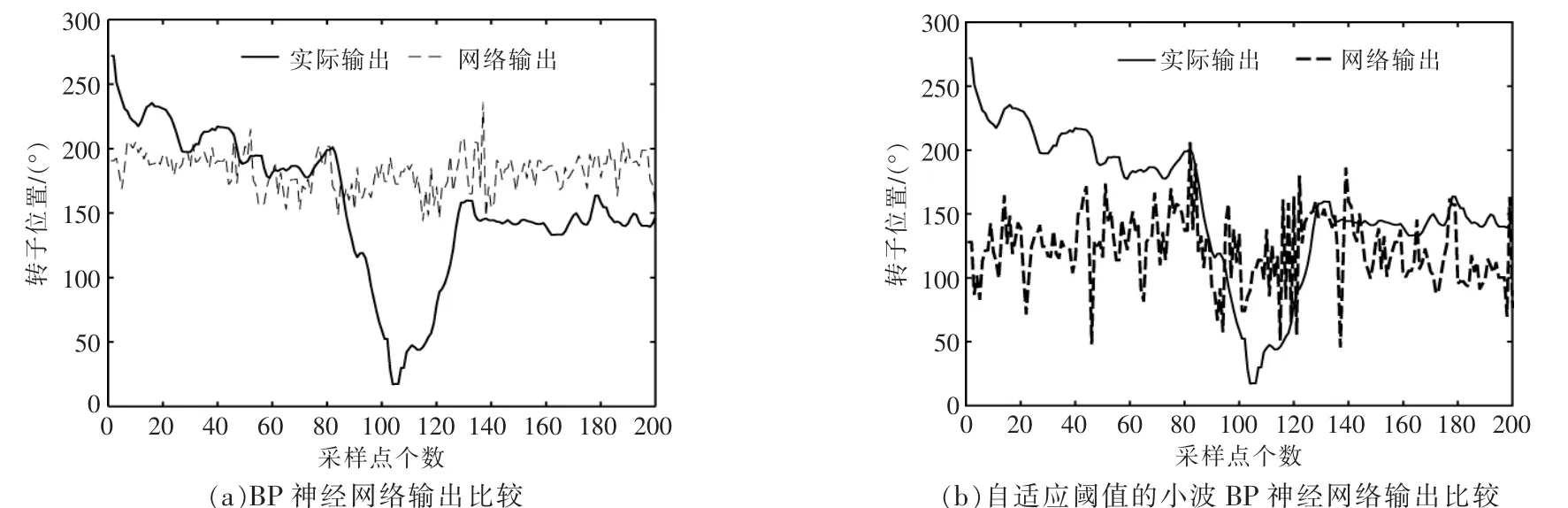
图7 故障训练网络输出与实际输出Fig.7 Comparison of fault training network output with actual output

图8 正常测试网络输出与实际输出Fig.8 Comparison of normal test network output with actual output

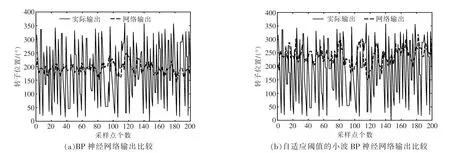
图9 故障测试网络输出与实际输出Fig.9 Comparison of fault test network output with actual output

由图6～9 可知， 自适应阈值的小波BP 神经网络的网络输出拟合实际输出的效果优于BP 神经网络。

（3）预测误差指标对比

本文用IE，IAE 和ISE 对以上4 组实验进行分析，将转子位置作为训练模型的观测指标，对比结果如表3～6 所示。

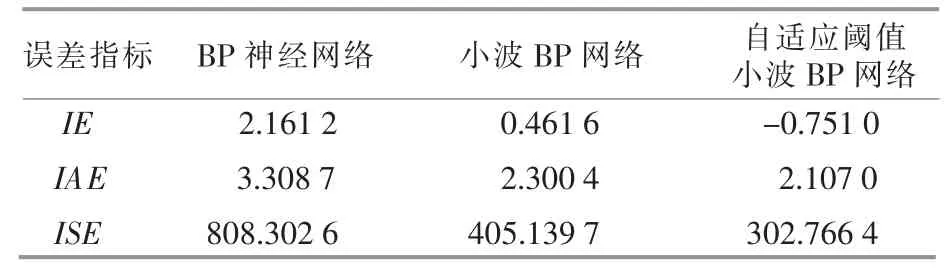
表3 正常训练数据误差指标对比Table 3 Comparison of normal training data error index

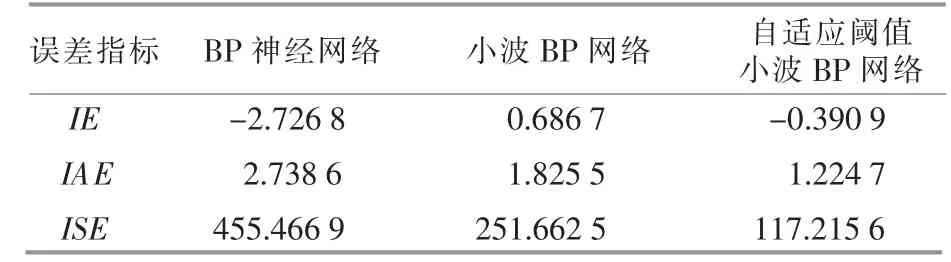
表4 故障训练数据误差指标对比Table 4 Comparison of fault training data error index

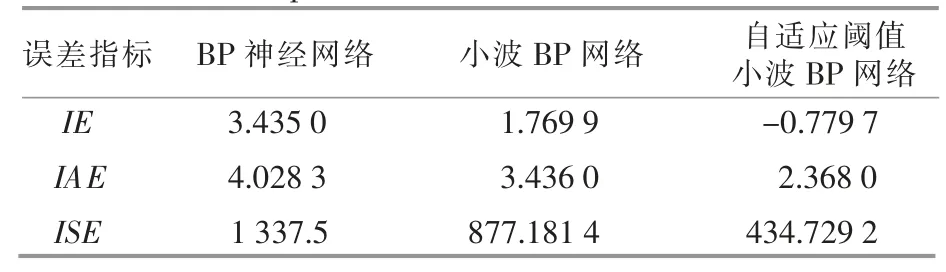
表5 正常测试数据误差指标对比Table 5 Comparison of normal test data error index

表6 故障测试数据误差指标对比Table 6 Comparison of fault test data error index

由表3～6 可知，在两种算法下，自适应阈值小波BP 神经网络得到的在正常训练、故障训练、正常测试和故障测试下的误差指标均最小。

综上， 自适应阈值小波BP 神经网络算法更适用于风电机组变桨系统的故障预测。

4 结论

本文从风电机组变桨系统故障预测入手，利用小波对提取的机械信号特征敏感的特点， 将小波分析引入到风电机组的故障预测中。 结合BP神经网络算法具有泛化能力强、 容错能力好的特点，将小波分解应用到BP 神经网络中。 针对小波消噪中阈值选取的不同对消噪效果影响较大的问题，引入一种自适应阈值小波去噪方法，通过调整自适应阈值函数，根据实际信号实现不同软、硬阈值的控制。 通过对比BP 神经网络算法、小波BP神经网络算法和自适应阈值小波BP 神经网络算法的试验结果， 发现自适应阈值小波BP 神经网络算法对风电机组变桨系统的故障预测具有更高的准确率。