基于强化学习和角度惩罚距离的冰晶连续优化算法
2021-02-27虞慧群
许 毅,冯 翔,2,虞慧群,2
(1.华东理工大学信息科学与工程学院,上海200237;2.上海智慧能源工程技术研究中心,上海200237)
全局优化问题广泛存在于工程、经济、生物、网络交通等领域,目前主要有两大类优化算法用于解决全局优化问题,一类是基于梯度的算法,一类是元启发式优化算法。然而许多基于梯度的算法,如拉格朗日乘子法、共轭方向法、投影罚函数法以及黄金分割法等,主要依赖于目标函数的梯度信息,而实际问题中的目标函数往往是不可导的,所以该类算法在解决实际问题时会受到很大的限制。
元启发式算法的优势在于它的灵活性,由于它仅需要通过观察输入和输出来解决优化问题,而无需考虑搜索空间的梯度,所以在解决各式各样的问题上具有高度的灵活性,同时,在算法中加入的随机因子也有助于避免陷入局部最优。基于这些优势,元启发式算法可应用于更广泛的领域中。
元启发式算法分为两大类:群体智能算法[1]和进化算法[2]。群体智能算法的基础主要来源于一些群体生物的集体智慧,将这些群体行为构建而成的模型作为解决复杂现实问题的框架,其中最常用的算法是粒子群算法(PSO)[3-4]和蚁群算法(ACO)[5]。此外,还有其他群体智能算法,如:灰狼群算法(GWO)[6-8]、人工蜜蜂群算法(ABC)[9]、樽海鞘群算法(SSA)[10]等。进化算法模拟了自然进化的过程,最著名的是遗传算法(GA)[11],其他的进化算法有差分演化算法(DE)[12]、生物地理优化算法(BBO)[13]等。
冬季湖水结冰是一种常见的自然现象。当湖水温度低至凝固点时,水分子就会凝结成冰晶。通常,影响湖水温度的因素有湖水的深度、大气的温度、湖面风的大小等。本文以找出湖水中心为目标,通过模拟湖水结冰的过程实现对连续极值问题的求解,提出了冰晶连续优化算法来解决全局优化问题。
冰晶连续优化算法在解决极值问题时会极度依赖于每次迭代时中心点的选取,这样算法容易陷入局部最优。受文献[14]中参考向量的启发,本文引入了角度惩罚距离策略来综合考虑中心点位置的选取,以达到平衡收敛性和分布性的目的。同时在新生冰晶的位置选择上,为了加速算法的收敛速度,受文献[15]中组选择策略的影响,引入了基于强化学习的概率更新策略,利用已有的先验知识对新生冰晶的位置作出指导,有效地提高了收敛速度。
1 基于强化学习和角度惩罚距离的冰晶连续优化算法
1.1 冰晶连续优化算法
1.1.1 初始化 算法开始时,湖水中会分布S个维度为n的晶体,即c i=(ci1,ci2,···,cin)∈Rn,初始化每个晶体的能量值Ei0=f(x),其中f(x) 为目标函数。
1.1.2 冰晶壳的生成 第一次初始化后,能量值最低的NS个晶体将会链接在一起,形成一层冰晶壳,形成冰晶壳的晶体不再加入到沉淀过程中。同时为了保证湖水中未析出晶体个数不变,将会重新生成NS个晶体,以替代形成冰晶壳的晶体。
1.1.3 湖水晶体的能量变化 未形成冰晶壳的晶体会发生能量变化,其能量随时间的变化公式为

1.1.4 冰晶壳的再生长 未结成冰晶壳的晶体在能量变化后,能量值最低的Np个晶体开始沉淀,沉淀过程中会被已结成冰晶壳的晶体吸收能量,从而加速沉淀并加入到已结成的冰晶壳中,这样扩大了冰晶壳的范围,而未沉淀的晶体将会参与到下次的能量变化和沉淀过程中。
图1为冰晶连续优化模型收敛示意图,其伪代码如下:


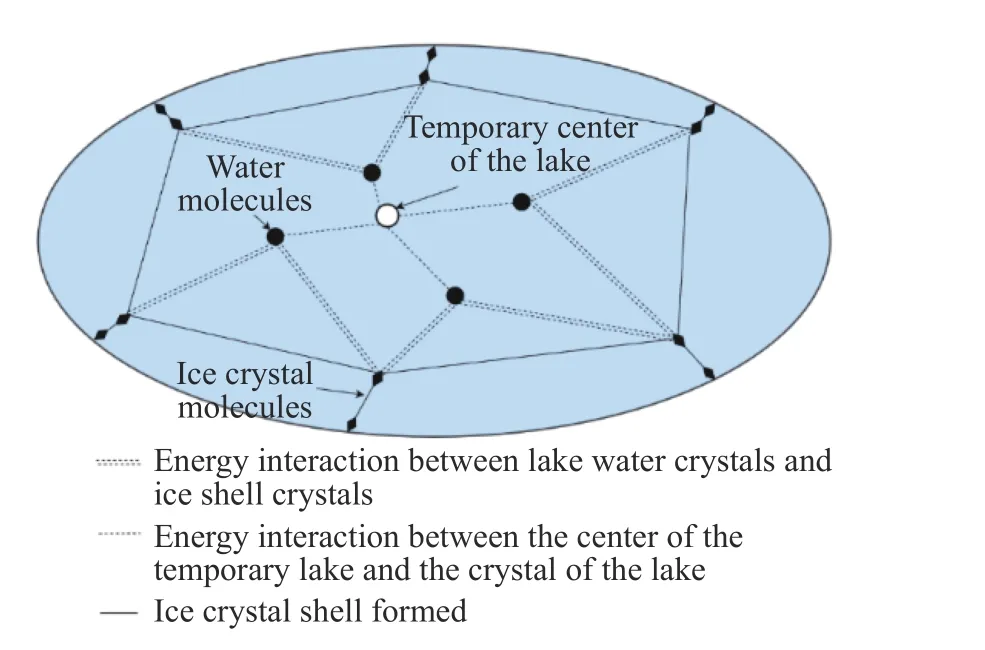
图1 冰晶连续优化模型收敛示意图Fig.1 Convergence diagram of ice crystal continuous optimization model
1.2 基于角度惩罚距离的偏差策略
由于湖水中心位置的不确定性,所以选择当前位置最好的点作为临时湖水中心,但这势必会导致晶体能量的变化产生偏差,即不能准确地计算出晶体从湖水中心获得的能量值。本文采用角度惩罚距离策略来消除临时湖水中心带来的偏差值。
1.2.1 多样性度量 受临时湖水中心影响,晶体的沉淀过程和结冰结果易陷入局部最优。本文采用角度信息来评价晶体的位置分布,从而消除临时湖水中心带来的收敛程度的影响。
对于晶体c i,多样性度量是指其与未结冰晶体中其他晶体的最小夹角,计算公式为
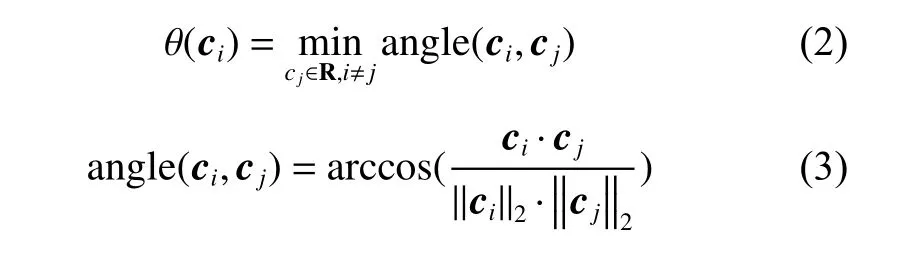

1.2.2 角度惩罚距离 在算法前期,应该使晶体的分布更为分散,即让冰晶壳的形成总是从外围向内部扩展,使之与实际湖水中心带来的能量变化的影响相符;而到了算法后期,在结冰范围越来越靠近湖水中心时,减少晶体的多样性,以期在较小的区域中更快地逼近湖水中心。为了消除湖水中心带来的偏差以及满足以上要求,针对1.1.3 节中晶体的能量变化公式,本文引入了角度惩罚距离策略。随着晶体结冰的进程,动态地调整算法在前后期晶体的分布和消除临时湖水中心带来的能量偏差。角度惩罚距离公式为

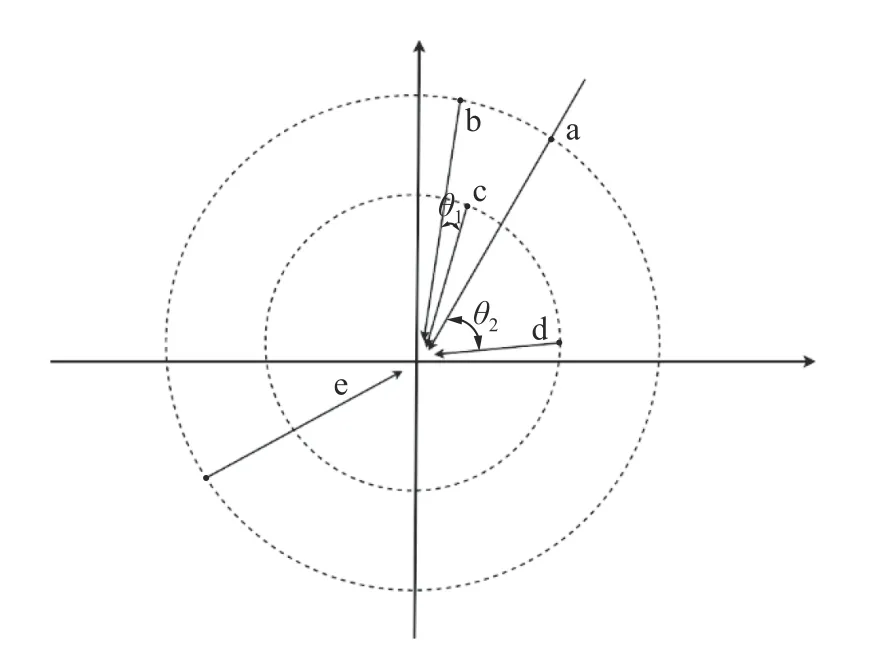
图2 基于角度惩罚距离的偏差策略示意图Fig.2 Deviation strategy based on angle penalty distance
通过角度惩罚距离选择出迭代过程中的临时湖水中心,与原本从目标函数得出的湖水中心相比,角度惩罚距离会考虑到多样性的影响,且是一个随迭代过程动态变化的值,能更好地体现实际湖水中心的位置。
1.3 基于强化学习的概率更新
经过能量交互后,能量较低的晶体将会沉淀并析出,析出的晶体则会链接在一起形成冰晶壳,冰晶壳的结冰范围为


为了保证湖水中的未析出晶体总数不变,在冰晶壳的范围内会生成新的晶体分子,以参与到下一次的迭代沉淀中。在[c j_min,c j_max] 范围内随机生成新的晶体,旨在后续迭代中不断形成冰晶壳,从而不断地逼近湖水中心。对于整个湖水能量体系来说,冰晶壳总是位于远离湖水中心的位置,随机生成的晶体极有可能会同样被分布到远离湖水中心的位置,很大程度地降低了湖面结冰的速度。为了让湖面尽快结冰,即加快冰晶算法的寻优速度,本文提出了基于强化学习的概率更新来加快晶体的沉淀过程。
强化学习[16-17]被定义为一个智能体在未知环境中如何采取动作以期获得最大的累计收益,每一步的选择都不仅仅只是影响到当前的收益。强化学习潜在的思想就是那些能使累计收益最大的动作有更大的可能被选择。
晶体的生成依赖于未沉淀晶体的位置。每次沉淀后,会保留有S−Ns个晶体继续参与下次迭代,新生的晶体会依概率Gt从保留的S−Ns个晶体中选择一个,出现在其附近。初始时,保留的晶体被选择的概率是相同的,但随着迭代,上一次保留的晶体可能会在这一次迭代中依旧存在,这时将会奖励这个晶体,并通过式(9)更新概率:

1.4 算法流程
为了尽量消除由于临时湖水中心的位置引起的能量变化误差和加快湖面结冰的速度,本文分别对临时湖水中心的选择和晶体的生成进行了改进,提出了基于强化学习和角度惩罚距离的冰晶优化算法(APD-CEO)。算法的伪代码如下:
输入:冰晶群大小S,最大迭代次数Tmax输出:湖水中心的位置
begin
(1)初始化S个冰晶,T= 0
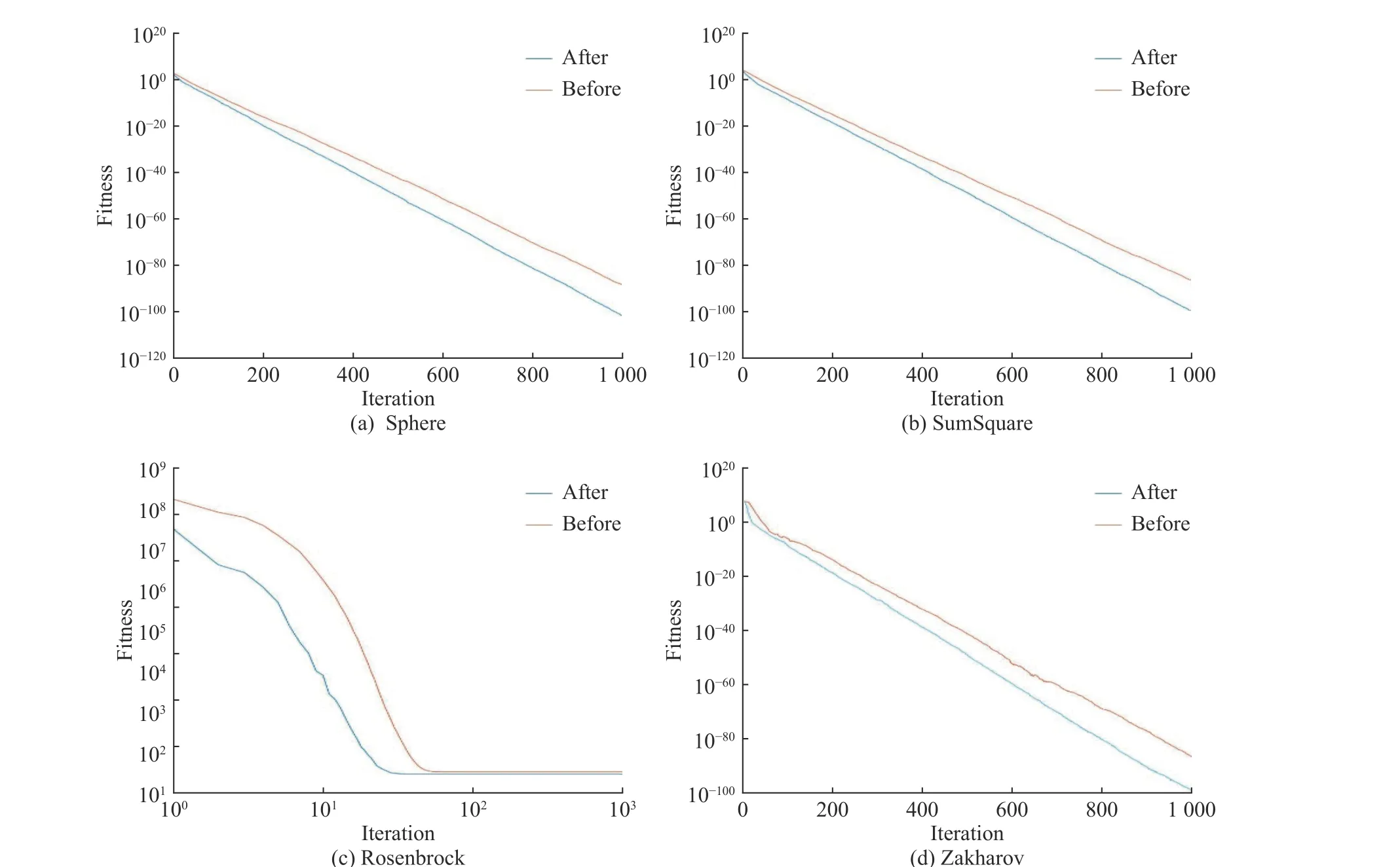
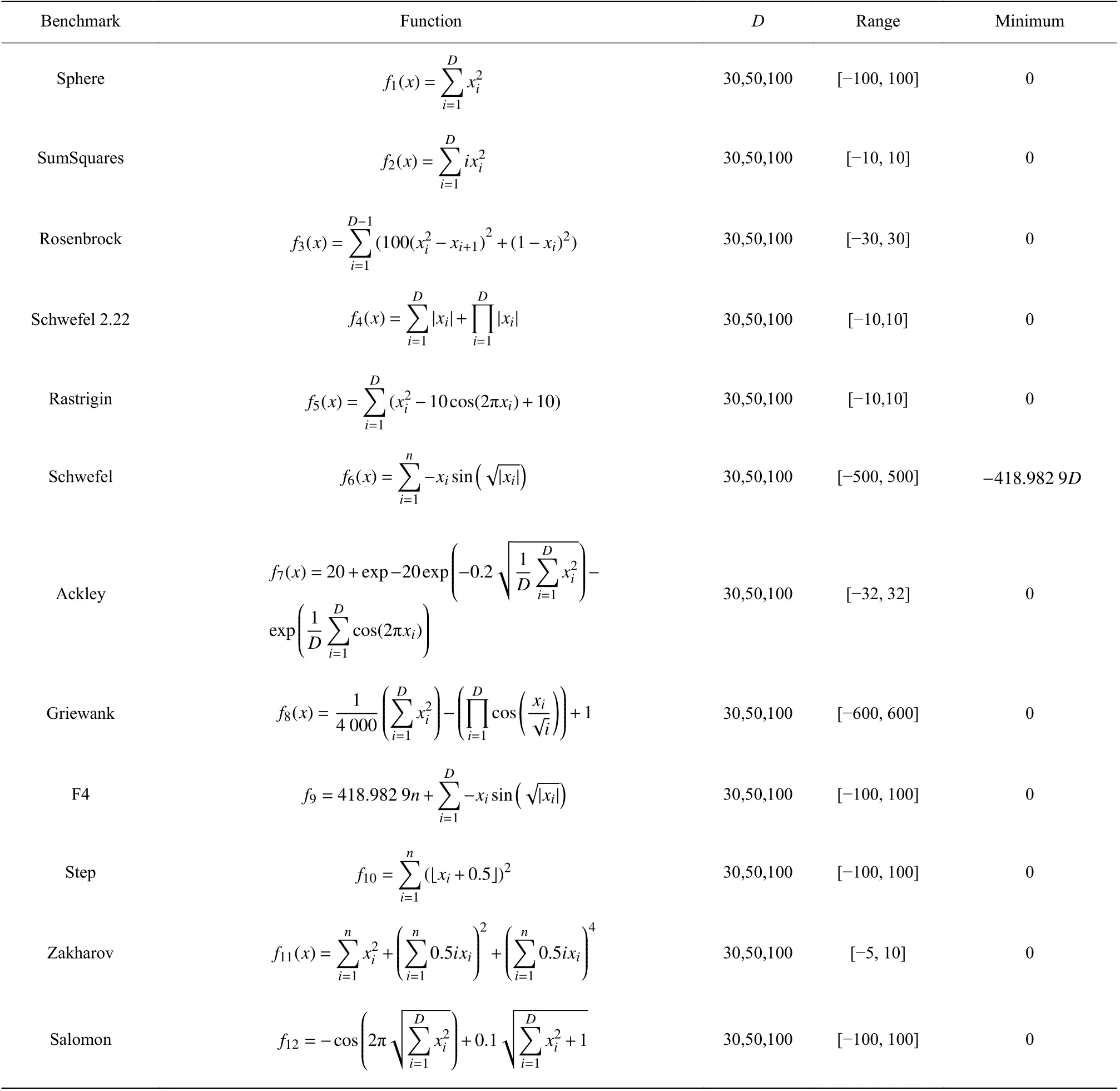
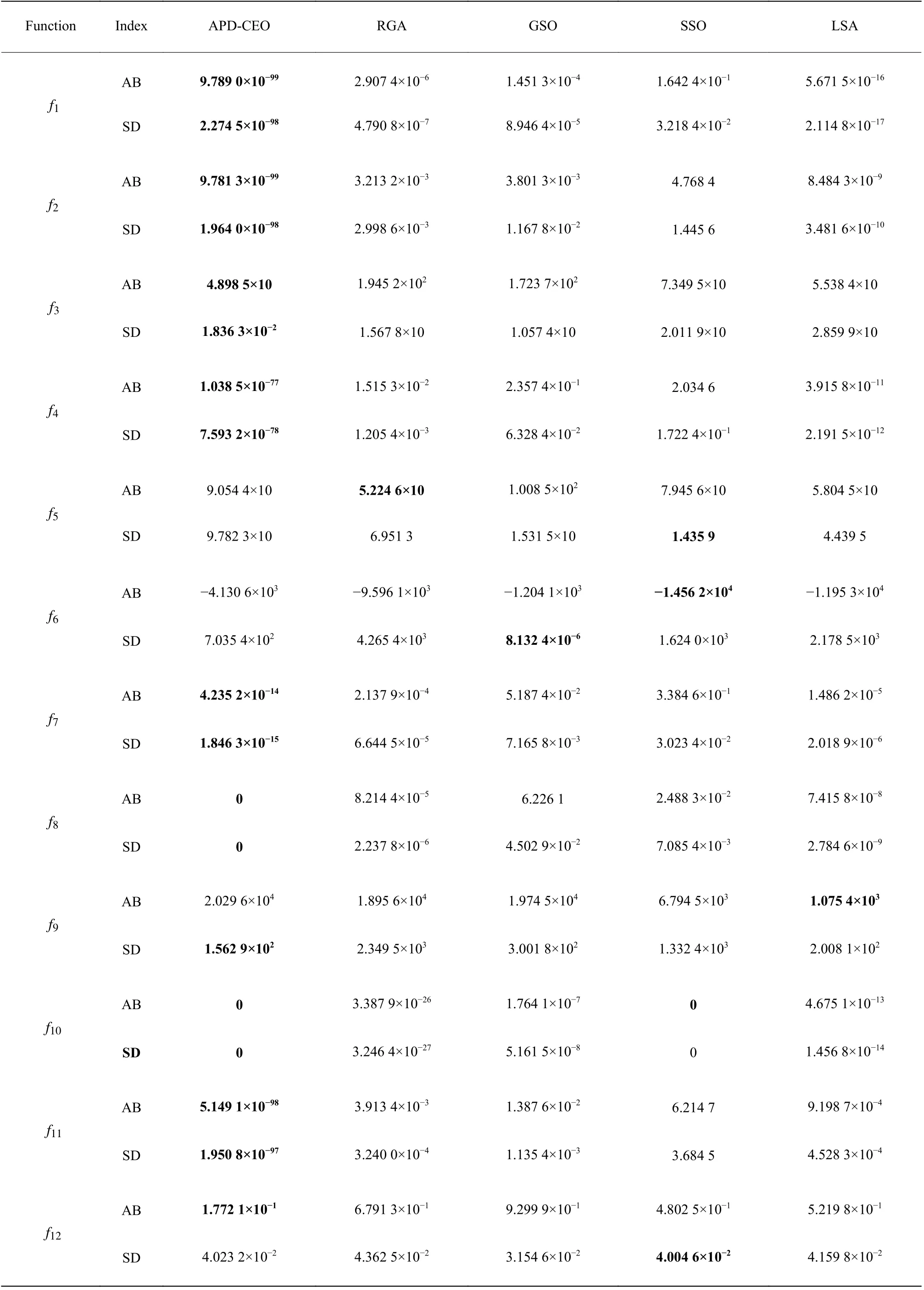
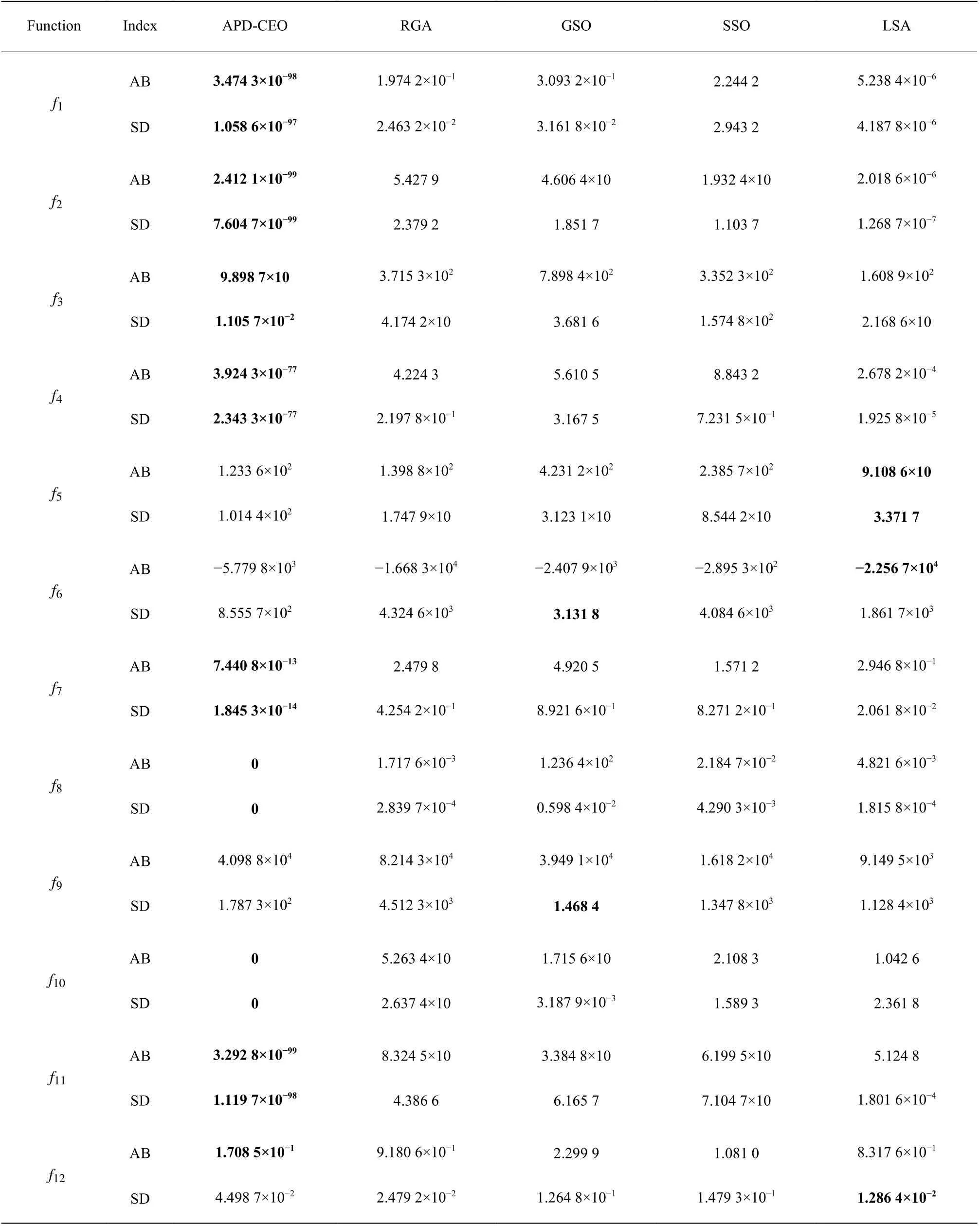
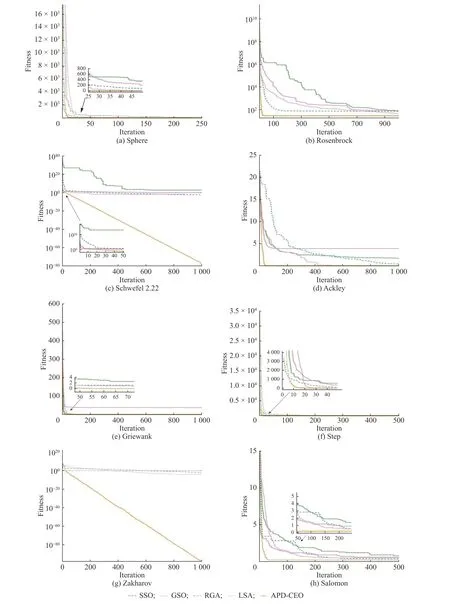
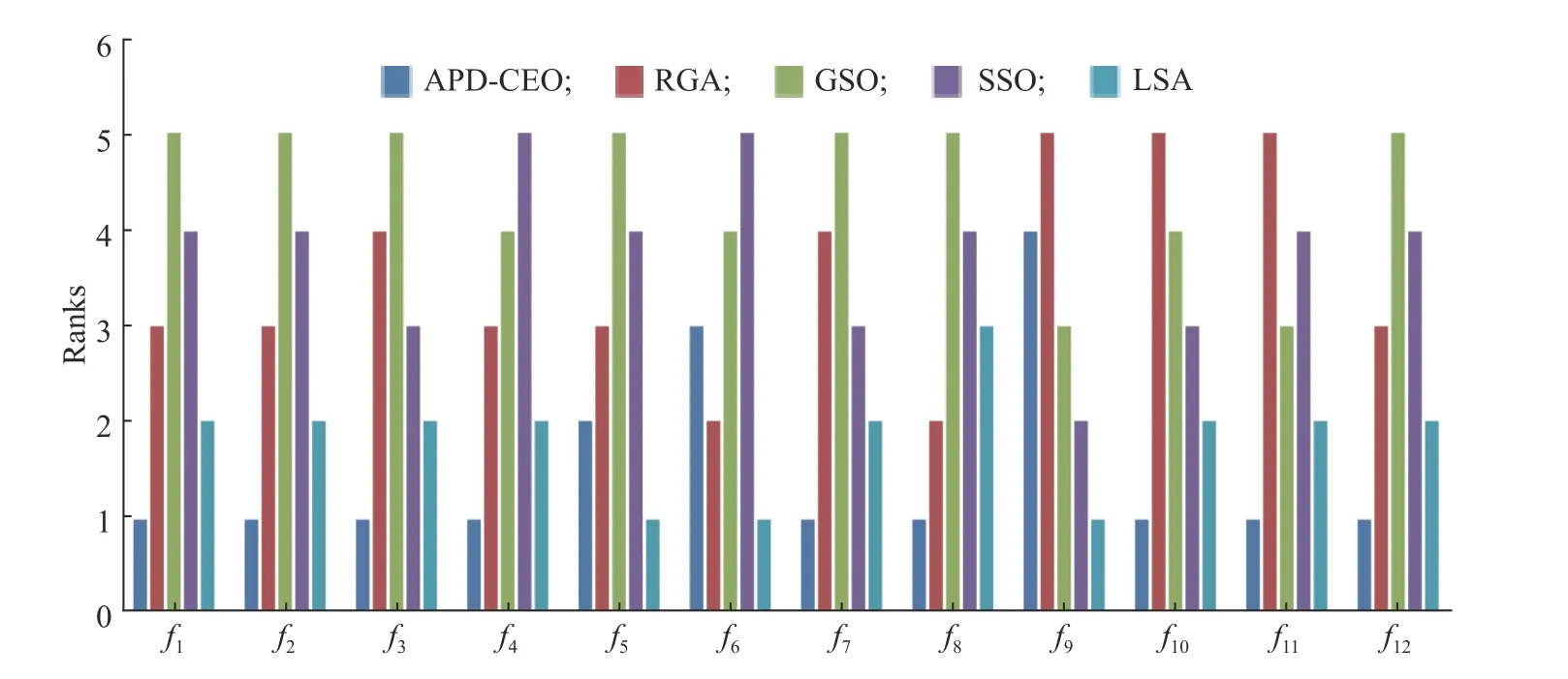
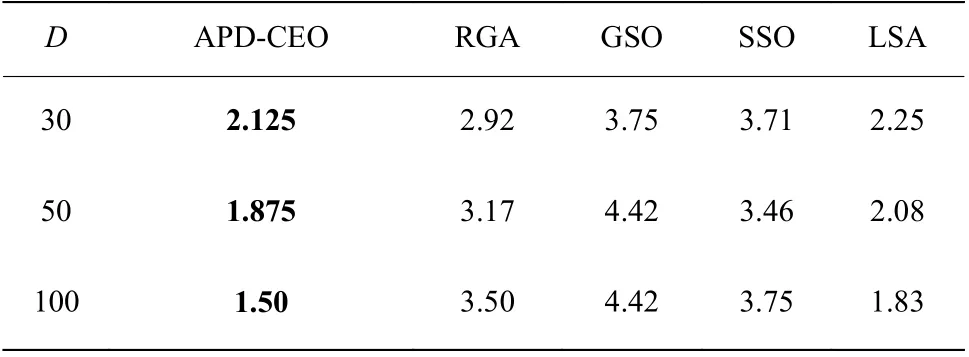
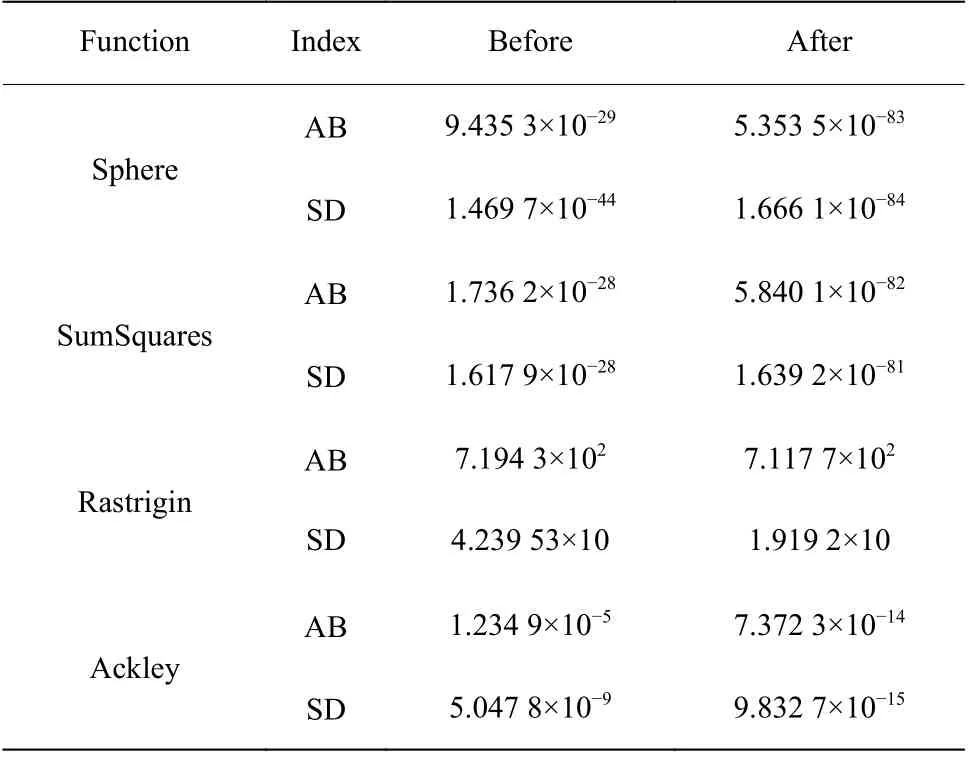
(2)whileT (3) 根据式(2)~式(5)计算角度惩罚距离,得出临时湖水中心 (4) 根据式(1),晶体能量发生变化 (5) 对于每个晶体: (6)if 晶体能量达到阈值 (7) 晶体开始沉淀,形成冰晶壳 (8) 根据式(9)计算晶体被选择的概率Gt (9) 根据式10 计算出新生晶体的位置 (10)输出湖水中心的位置 end 湖水能量体系可以看作是一个能量消耗系统,其整体的能量会随着时间而减少。APD-CEO 算法中的每个晶体都会在空气中散发能量,并且有可能会被冰晶吸收能量,因此构成了一个能量衰减的动态系统。本文通过定义一个正定的Lyapunov 函数来判定该动态系统的稳定性。 证明 对于APD-CEO 算法,会存在3种状态的晶体,即湖水中心的晶体、处于湖水边沿的晶体和已经析出的晶体。对于已经析出的晶体,其能量稳定,状态不再变化,已变为稳定的状态。 代入相应的计算公式,有 湖水中心晶体通过式(4)来判断,湖水中心Lcenter由角度惩罚距离和初始能量共同决定。当算法步入迭代后期,式(5)中Z(θ)的值趋近于0,此时的湖水中心总是选取当前能量最大的湖水晶体,即湖水中心分子总是选取每次迭代中的最大值。而湖水体系是一个能量衰减的系统,所以湖水中心分子最终会收敛到一个稳定的值。 由上述可知,基于Lyapunov 稳定性定理,APDCEO算法将会收敛到一个平衡的状态。 实验环境:Matlab R2014b on the HPCCof Lenovo Shenteng 6800,该集群拥有8 个计算节点和1 个总控节点。每一个计算节点是一台高性能服务器,内存为24 GB,四核2.4 GHz 中央处理器。 12个基准函数的描述如表1所示。将APD-CEO算法与RGA[18]、GSO[19]、SSO[20]和LAS[21]算法进行对比来验证算法的性能。在所有的比较示例中,群体规模均为100,最大迭代次数均为1 000。每个算法的参数设置如表2所示。 表3示出了本文算法与其他4种算法在函数维度D为30维的比较结果,实验运行次数为30次。性能评价指标为平均最佳解(AB)、最佳解的标准差(SD)。从表中可以看出本文算法只有在f5、f6和f9函数上的AB指标不理想;在f2和f3函数上,算法性能排第二;在其余的7个函数中都能取得最优的AB和SD指标。表4示出了算法在50维基准函数下的实验结果,与30维基准函数相比,本文算法表现得更好,除了上述的7 个函数外,还在f2和f3函数上取得了最好的结果。 表1 基准测试函数Table 1 Benchmark functions 表2 各个算法的参数设置Table2 Parameter settings of each algorithms 表3 APD-CEO、RGA、GSO、SSO和LSA 在基准函数上的实验结果(D=30)Table 3 Experimental resultsof APD-CEO,RGA,GSO,SSO and LSA on benchmark functions (D=30) 表4 APD-CEO、RGA、GSO、SSO和LSA 在基准函数上的实验结果(D=50)Table 4 Experimental resultsof APD-CEO,RGA,GSO,SSO and LSA on benchmark functions (D=50) 为了测试本文算法在高维度上的性能表现,提升基准函数的维度到100维,实验结果如表5所示。与50维的结果类似,本文算法在9个基准函数上取得了最好的效果,同时在f8和f10函数中依旧取得了标准最小值0。 图3为不同优化算法在30维的基准函数上的搜索演化曲线图,可以更直观地看出算法的优劣性。基准函数分别为f1、f3、f4、f7、f8、f10、f11、f12,从图中可以看出,APD-CEO的收敛速度最快。 表5 APD-CEO、RGA、GSO、SSO和LSA 在基准函数上的实验结果(D=100)Table 5 Experimental resultsof APD-CEO,RGA, GSO,SSOand LSA on benchmark functions (D=100) 图3 5种算法在8个30维基准函数上的演化曲线Fig.3 Evolution curves of the five algorithms on eight benchmark functions with 30 dimensions 为了更进一步分析算法的有效性,以Friedman排名来进一步说明。图4示出了不同算法100维下在12个基准函数上的排名,可以看出,除了函数f5、f6和f9之外,APD-CEO在5种算法中表现最好。表6列出了不同维度下算法在基准函数上的Friedman 平均排名。可以看出5种算法的优化性能表现排名为APD-CEO、LSA、RGA、SSO和GSO。 为了验证角度惩罚距离在冰晶连续优化算法中的有效性,将加入角度惩罚距离策略后的冰晶连续优化算法与未加入任何策略的冰晶连续优化算法进行了性能比较。实验结果如表7所示。 图4 各算法的Friedman 排名Fig.4 Friedman ranksof each optimization algorithms 表6 各优化算法在30、50 和100维下的平均排名Table 6 Average ranking of each optimization algorithms 表7 角度惩罚距离策略的有效性Table7 Effectiveness of angle penalty distancestrategy 本文对加入基于强化学习的概率更新策略前后的算法进行了比较,实验结果如图5所示。After 表示加入概率更新后的优化曲线,Before表示加入之前的优化曲线。可以看出,加入概率更新后,曲线下降得更快,优化算法能更快地收敛,并且保持在1 000次迭代后拥有更好的结果。实验表明基于强化学习的概率更新能给算法带来优势。 通过模拟湖水结冰的过程来实现对连续极值问题的求解,提出了冰晶连续优化算法以解决全局优化问题,并在其基础上加入了角度惩罚距离策略和基于强化学习的概率更新策略,使得中心点的选择能同时考虑到收敛性和分布性,以及晶体的生成能借鉴已有的先验知识,加速了算法的收敛速度和准确度。将本文算法与其他4种对比算法在12个基准函数上进行测试,并分别在30维、50维和100维上检验了算法性能。实验结果表明,与其他4种算法相比,APD-CEO能表现出良好的性能,且在高维度上能表现得更好。为了更进一步测试算法性能,使用Friedman Test 非参数统计方法分析了本文算法的表现。本文主要探讨的是算法在单目标极值优化问题上的性能表现,在接下来的工作中,我们将更多地研究算法在多目标优化问题中的表现。 图5 加入概率更新策略前后算法的演化曲线Fig.5 Evolution curvesof thealgorithms before and after joining probabilistic update atrategy2 算法收敛性证明


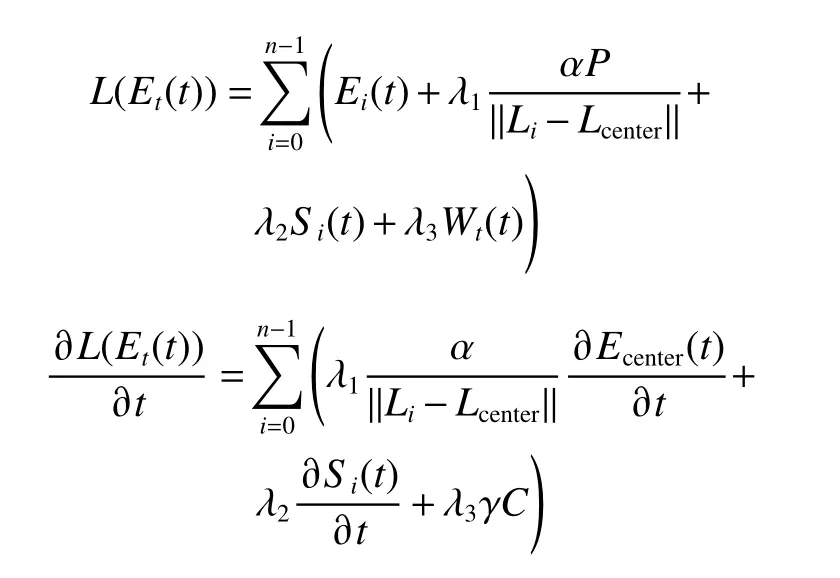

3 实验与分析
3.1 算法的有效性比较


3.2 角度惩罚距离的有效性
3.3 基于强化学习的概率更新策略的有效性
4 结束语