以生为本，让计算教学彰显活力

2021-02-27范海荣

名师在线 2021年5期

关键词：小数点加减法整数

范海荣

（江苏省启东实验小学，江苏启东 226200）

引言

教师容易按照成人的思维习惯来看待儿童的学习，往往会造成一定的冲突，其主要原因是成人没有真正认识儿童和理解儿童，没有站在儿童的视角指导儿童。笔者试图结合计算教学中的点点滴滴，谈些粗浅的认识，以求教同行。

一、把握儿童的已学知识

学习是儿童基于原有知识经验的自我建构，其原有的知识结构对新知的学习具有很重要的作用。儿童头脑中的知识结构组织得越好，就越有利于保存和应用，特别是面对新的学习情境时，其就越容易提取出来，以帮助幼儿适应新知的学习[1]。

以苏教版五年级上册“小数加减法”计算“4.75+3.4”一课为例，在学习本课前，学生已经学习了整数加减法，知道了数位对齐、个位加起、满十进一等法则，并在三年级时学习了一位小数加减法，知道了要小数点对齐。因此，多数教师臆定本节课的重点为小数点对齐。然而实际情况并非如此。笔者在听课中发现，在尝试列竖式中，有三分之一以上的学生出现了意想不到的情况（见图1）。

图1

细细思考，这样的列式又是如此的“合情合理”，因为整数加减法十分强调数位对齐，当两个整数加数位数不同时，更为直观和现实的是末位对齐。可见，末位对齐在学生头脑中已根深蒂固。而在教学“一位小数加减法”中，教师又十分强调小数点对齐。于是，学生创造出了既遵循末位对齐，又遵循小数点对齐的“怪”式，暴露出学生的真实思维。所以，教师应多从儿童的视角关注儿童的已有，把握真实的教学起点。

二、丰盈儿童的体验

数学教学要引领儿童用自己的方式经历、体验、复演人类创造知识的生动历程，让他们在数学知识的创造活动中与生产知识的人和历史进行对话。

例如，在教学苏教版四年级上册“乘法和加、减法的两步混合运算”一课时，一位教师大胆地放弃了书本创设的情境，防止学生产生计算顺序来源于具体实际问题这一错误认识。课的伊始，教师便出示了口算题“12+7+5”，让学生知道是这道题要从左往右依次计算，再把5 变为7，得到算式“12+7+7”。然后，教师让学生说说是如何口算的。大部分学生依然选择依次连加，也有少数学生说出先算“2×7=14”，再算“12+14=26”。接着，教师在此算式的后面再加上3个7，得到“12+7+7+7+7+7”。学生不约而同地发出了惊讶的声音。一会儿，有学生大声说出答案是47。教师连忙问：“你是怎么算的？”学生说：“算式里有5 个7，可以先算5×7=35，再算12+35=47。”教师进一步追问：“为什么不用从左往右的方法呢？如果用从左往右的方法会怎样呢？”在师生一齐验证的过程中，学生真真切切地感受到计算方法的优劣。计算效率的极大反差所带来的强烈冲击强化了学生的学习体验。在两种算法的直接对比中，学生真切地体验到先算乘法的便捷与合理性，从而顺利地将头脑中根深蒂固的运算顺序由原来的从左往右扭转成先乘法。

三、等待儿童的发现

知识的获得常常是一个困难、缓慢的过程。只有从容地、缓缓地让儿童说一说、议一议，儿童才能自由地发展自己的心智。

例如，在教学苏教版五年级上册“小数乘法和除法”例5 一课时，笔者听取青年教师同课异构时发现，不少学生在尝试计算“7.98÷4.2”时，出现了与预设不一致的情况（见图2）。

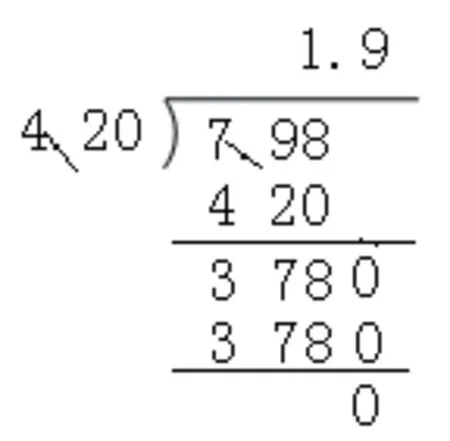
图2

对此，教师做出了两种不同的教学安排。一位教师提出明显带有倾向性的问题：“这样计算，简便吗？”于是，一些学优生心领神会，围绕简便这一思路展开讨论，发现根据商不变的性质，“798÷420”和“79.8÷42”的结果相同，但显然“79.8÷42”要简便些。但课后练习令人大跌眼镜，仍有学生顽固地采用把被除数和除数都转化成整数的计算方法。

吸取了上一位教师的教训，在学生做出上面的算法后，教师没有急于求成，而是让全体学生用两种方法笔算“0.024÷4.8”。一些学生有所感悟，跃跃欲试地要表达观点。教师不慌不忙，又让学生口算练习了一定数量的习题。通过对比，学生体会到两种方法的共同点和不同点，课后练习也十分理想。由此看来，教师要舍得时间让学生体会，等待学生慢慢感悟。

四、催生儿童的创造

著名教育家陶行知先生认为，儿童是天生的创造家；儿童是积极的探索家；儿童是自主的管理者。因此，教师要充分关注儿童的创造潜能，为他们搭建展示的舞台，疏通“再创造”的通道。

例如，对于苏教版六年级上册中“分数除法”的知识，教材依次安排了“分数除以整数”“整数除以分数”“同分母分数除法”，并在此过程中逐步引导学生总结计算法则。而异分母分数除法安排在随后的练习中，由学生根据得出的计算法则“照章办事”。这样的安排显然降低了学生的学习难度，可谓用心良苦，同时也有回避“异分母分数除法”难点之嫌。事实上，我们远远低估了学生发现和创造的能力。笔者在完成教材的预设后，抛出问题：“除了刚才学的方法，还有其他方法能解决9 3 10 10÷吗？可以结合书本的直观图来思考。”教室里一开始十分安静。终于，有学生怯怯地举手起来，说：“能倒满3 杯，我是在图上画，用9÷3 得到的。”说着，这位学生展示了自己的思考过程（见图3）。