基于微分几何法的非线性分数阶悬架主动控制
2021-02-26常宇健田沃沃陈恩利李韶华
常宇健, 田沃沃, 金 格, 陈恩利, 李韶华
(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;2.石家庄铁道大学 电气与电子工程学院,石家庄 050043)
目前对于油气悬架、空气悬架和磁流变悬架的研究主要考虑其部分弹性或是阻尼特性,并没有反映实际悬架阻尼材料的记忆特性。因此国内外学者基于分数阶模型具有良好的记忆功能,提出采用分数阶微积分理论建立黏弹性悬架的动力学模型。Oustaloup等[1]首次提出CRONE悬架,该悬架采用分数阶阻尼的机械系统代替传统被动悬架中的弹簧和阻尼器。文献[2-4]针对油气悬架的整数阶模型不能准确描述其多相介质力学特点,提出采用分数阶微积分理论建立其Bagley-Torvik方程,并验证了该模型的可行性。文献[5]将分数阶微分引入液压气动悬架建模中,并通过仿真和实验证明了分数阶液压气动悬架模型的有效性。文献[6]提出一种能够准确描述空气弹簧记忆特性的分数阶模型。文献[7]利用分数阶模型描述磁流变阻尼器的阻尼特性,该模型比整数阶模型具有更高的拟合精度。文献[8]建立了MR阻尼器的分数阶模型,并且分析了该模型的动力学特性。上述研究都验证了分数阶微积分理论在汽车悬架系统建模中的适用性及有效性,为今后分数阶悬架模型的研究奠定了基础。
为改善分数阶悬架系统垂向动力学性能,文献[9]利用粒子群算法研究了被动分数阶汽车悬架参数的优化设计,研究结果表明参数优化后的分数阶悬架的乘坐舒适性得到明显改善。然而该被动分数阶悬架模型忽略了非线性刚度对系统的影响,因此并不能准确反映实际悬架性能。虽然文献[10-11]对汽车悬架系统中的线性阻尼成分进行改进,建立由分数阶阻尼和非线性弹簧组成的悬架系统,并采用整数阶PID控制和分数阶PIλDμ控制改善汽车的行驶性能。但是,这些研究仅仅针对磁流变悬架,而且忽略了分数阶磁流变Bingham模型中补偿器产生的力和库伦阻尼力,这就造成了分数阶悬架模型的研究具有特定的适用范围。因此本文在传统线性刚度和线性阻尼的悬架模型基础上进行改进,增加了非线性刚度和分数阶阻尼,使分数阶悬架模型具有更广的适用范围。另外,PID控制针对非线性系统通常控制效果并不理想,因此对于非线性分数阶悬架系统控制仍需进一步深入研究。
对于传统非线性主动悬架系统的研究,文献[12-14]分别针对特种车辆主动油气悬架、矿用汽车主动油气悬架和导弹发射车主动油气悬架进行非线性系统建模,然后基于微分几何法将非线性系统反馈线性化,并利用PID控制和最优控制进行控制研究。结果表明该非线性系统的控制策略具有算法设计简单、控制效果良好等特点。基于上述研究成果,本文基于微分几何法对含分数阶微分的非线性系统进行反馈线性化,从而将低了原系统的复杂性。
本文基于分数阶微积分理论对传统非线性悬架系统模型进行改进,建立了相比传统整数阶模型更为精确的1/4车二自由度非线性分数阶悬架模型。为提高汽车的行驶过程中的动态性能,分别设计PID控制器和基于微分几何法反馈线性化LQR控制器对该悬架系统进行主动控制,对两种主动悬架在随机路面输入和脉冲路面输入两种激励下三种性能时域响应结果以及两种主动控制力进行对比分析。
1 非线性分数阶主动悬架系统建模
1.1 1/4车二自由度主动悬架模型
图1为1/4车二自由度非线性分数阶主动悬架系统。
如图1所示,非线性分数阶主动悬架系统中弹性力包括一次线性恢复力和三次非线性恢复力,主动悬架弹性力为
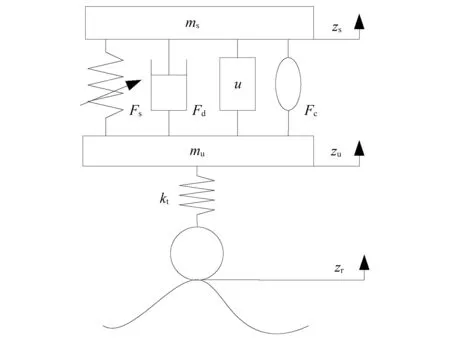
图1 1/4车二自由度主动悬架系统结构图Fig.1 Structural diagram of 2-DOF active suspension system for 1/4 vehicle
Fs=ks(zs-zu)+εks(zs-zu)3
(1)
式中:zs为簧载质量位移;zu为非簧载质量位移;ks为弹簧刚度;ε为非线性系数。
主动悬架系统中线性阻尼力为
(2)
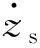
分数阶微积分主要有3种定义方式[15], Riemann-Liouville定义、Grunwald-Letnikov定义和Caputo定义。本文利用Caputo分数阶微分描述悬架系统中的分数阶阻尼力,Caputo定义式为
(3)
式中:0,t为分数阶微分上下限;α为分数阶微分阶次;Γ(·)为Gamma函数。
分数阶阻尼力为
Fc=hDp(zs-zu)
(4)
式中:h为分数阶微分系数;p为分数阶微分阶次,且满足0≤p≤1。
根据牛顿第二定律建立该系统的微分方程为
(5)

1/4车二自由度非线性分数阶悬架系统参数选取为ms=240 kg,mu=36 kg,ks=16 000 N/m,ε=0.1,c=1 650 N·s/m,kt=160 000 N/m,h=1 000,p=0.5。
1.2 分数阶微分的Oustaloup滤波器近似算法
由于非线性分数阶悬架系统较为复杂,为方便利用Matlab/Simulink进行仿真分析,本文利用Oustaloup滤波器算法[16]对分数阶微分项进行近似计算。即在选定的频率段(ωb,ωh)内做分数阶算子sp的近似替代,根据该思想构造的Oustaloup滤波器为
(6)
式中:M为滤波器阶次,滤波器的零点为
极点为
根据Oustaloup滤波器近似算法,构造一个频率段为(0.001 rad/s,1 000 rad/s),阶次为M=5的滤波器近似代替非线性分数阶悬架系统中的Caputo分数阶。
1.3 路面输入模型的建立
1.3.1路面随机输入建模
为了能够真实反映汽车在实际路面的行驶性能,本文利用Matlab/Simulink建立滤波白噪声随机路面作为1/4车二自由度非线性分数阶悬架系统的输入模型,即
(7)
式中:q(t)=zr(t)为路面位移;η1为下截止空间频率,η1=0.011 m-1;v0为车速,v0=10 m/s;η0为参考空间频率,η0=0.1 m-1;Gq(η0)为路面不平度系数,Gq(η0)=256×10-6m3;w1(t)是均值为0、方差为1的Gauss白噪声。
1.3.2 路面脉冲输入建模
根据GB/T 4970—2009《汽车平顺性试验方法》规定[17],采用三角形凸块描述路面脉冲输入,如图2所示。

图2 三角形凸块Fig.2 Triangle bump
三角形凸块的长度l=0.4 m,高度H=0.04 m,在离凸块L处汽车以v0直线匀速驶向凸块[18],如图3所示。

图3 汽车驶过三角形凸块的力学模型Fig.3 Mechanics model of a automobile running triangle bump
路面脉冲输入时域模型为
(8)

2 基于PID控制器的分数阶主动悬架
为提高汽车的乘坐舒适性和行驶安全性,需要对非线性分数阶悬架系统车身加速度、悬架动挠度和轮胎动载荷进行协同控制。本文设计三个PID控制器分别以上述三个性能指标为控制量进行控制,并将控制量期望值均设置为0,构造控制器参数优化目标函数为
(9)
PID控制器的输入信号为
(10)
PID控制器的输出信号为
(11)
式中,KPi,KIi,KDi(i=1,2,3)分别为PID控制器的比例、积分、微分系数。
基于PID控制器的非线性分数阶主动悬架的控制力为

u3(0-(zu-zr))
(12)
通过经验法并不断分析响应曲线,多次调节后可得到满足需求的整定参数如表1所示。

表1 PID控制器整定参数Tab.1 PID controller setting parameters
3 基于反馈线性化LQR控制器分数阶主动悬架
为改善汽车行驶过程中悬架系统的动态性能,本文利用微分几何法[19]将非线性分数阶悬架系统反馈线性化,针对线性系统利用LQR控制获得最优控制律,通过非线性状态反馈获得悬架系统的控制律。
3.1 非线性分数阶悬架系统状态空间表示


[x1x2x3x4]T
(13)

[y1y2y3y4]T
(14)


(15)
式中:

其中,

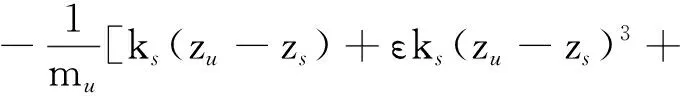
3.2 输出函数各阶李导数对x偏导计算
令h1(x)=x1,当k=0时,有
(16)
当k=1时,有
(17)
由此可得相对阶r=2,则有

(18)
η=[0 0 -1 0]T
(19)

(20)
则

(21)
同理可知:
令h2(x)=x2,相对阶r=1
u2=-[ks(zs-zu)+εks(zs-zu)3+
(22)
令h3(x)=x3,相对阶r=2
u3=-[ks(zs-zu)+εks(zs-zu)3+
(23)
令h4(x)=x4,相对阶r=1
u4=ks(zs-zu)+εks(zs-zu)3+
(24)
3.3 非线性分数阶悬架系统反馈线性化
通过对式(21)、式(22)、式(23)和式(24)进行比较和分析,选取非线性分数阶悬架系统的控制律为
u=ks(zs-zu)+εks(zs-zu)3+
(25)
将式(25)代入式(15)中可得
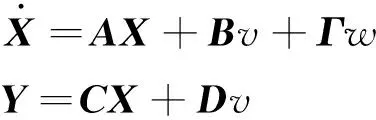
(26)
其中,
3.4 LQR控制器设计
为提高乘坐舒适性和操纵稳定性,针对非线性分数阶悬架系统设计了LQR控制器,该控制器性能指标函数的矩阵形式为
(27)
其中:
Q=CTMC
R=DTMD+ρ
M=diag[q1q2q3q4]
式中,q1,q2,q3,q4分别为车身加速度、悬架动挠度、轮胎动载荷和减震器能耗加权系数;ρ为加权系数;各个系数取值分别为q1=636,q2=3 030,q3=1 012,q4=1,ρ=1×10-7。
LQR控制律为
v=-R-1(BTP+WT)X=KX
(28)
式中,P为黎卡提矩阵方程式(29)的解,W=CTMD。
ATP+PA-(PB+W)R-1(PTB+W)+Q=0
(29)
计算可得LQR最优控制律为
v=16 970x1+30x2-25 861x3-1 346x4
(30)
将式(30)代入式(25)可得基于微分几何法反馈线性化LQR非线性分数阶主动悬架的最优控制力为

hDp(zs-zu)-(16 970x1+3 076x2-2 5861x3-1 346x4)
(31)
由此可得到非线性分数阶悬架系统反馈线性化模型的LQR控制系统框图如图4所示。

图4 LQR控制系统框图Fig.4 Diagram of LQR control system
4 仿真分析
利用Matlab/Simulink建立1/4车二自由度非线性分数阶被动悬架、基于PID控制的主动悬架以及基于微分几何法反馈线性化LQR控制的主动悬架的仿真模型。Simulink主动悬架仿真图如图5所示。经过仿真,三种悬架在随机路面激励下三个性能指标时域响应结果对比如图6、图7和图8所示;在脉冲路面激励下三个性能指标时域响应结果对比如图9、图10和图11所示。

图5 Simulink主动悬架仿真图Fig.5 Simulink active suspension simulation diagram

图6 车身加速度时域响应对比Fig.6 Time domain response comparison of vehicle body acceleration
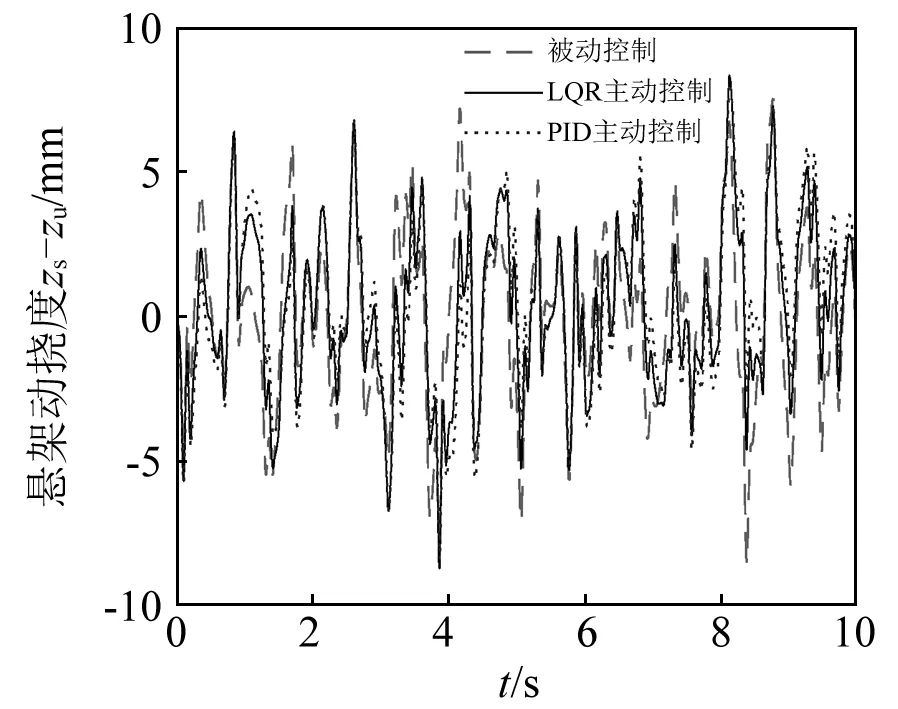
图7 悬架动挠度时域响应对比Fig.7 Time domain response comparison of suspension dynamic deflection
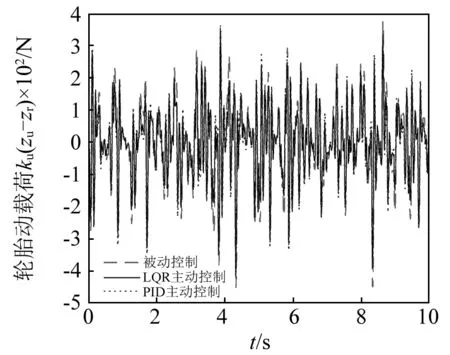
图8 轮胎动载荷时域响应对比Fig.8 Time domain response comparison of tyre dynamic load

图9 车身加速度时域响应对比Fig.9 Time domain response comparison of vehicle body acceleration

图10 悬架动挠度时域响应对比Fig.10 Time domain response comparison of suspension dynamic deflection

图11 轮胎动载荷时域响应对比Fig.11 Time domain response comparison of tyre dynamic load
基于PID控制的主动悬架和基于微分几何法反馈线性化LQR控制的主动悬架在随机路面激励和脉冲路面激励下的主动控制力对比如图12和图13所示。

图12 主动悬架控制力对比Fig.12 Active suspension control force comparison

图13 主动悬架控制力对比Fig.13 Active suspension control force comparison
含分数阶非线性的被动悬架、基于PID控制器的主动悬架和基于微分几何法反馈线性化LQR控制器的主动悬架在随机路面输入和脉冲路面输入激励下,车身加速度、悬架动挠度和轮胎动载荷的均方根值分别如表2和表3。

表2 性能指标均方根值数值表Tab.2 Root mean square value number table of performance indicators

表3 性能指标均方根值数值表Tab.3 Root mean square value number table of performance indicators
通过对比非线性分数阶被动悬架、基于PID控制器的主动悬架和基于反馈线性化LQR控制器的主动悬架的时域响应性能指标均方根值数值表可知,在随机路面输入激励下,两种主动悬架车身加速度分别降低到77.38%和74.94%,悬架动挠度分别降低到96.70%和94.61%,轮胎动载荷分别降低到91.46%和86.51%;在脉冲路面输入激励下,两种主动悬架车身加速度分别降低到80.73%和75.21%,悬架动挠度分别降低到95.10%和98.99%,轮胎动载荷分别降低到70.78%和56.36%。
通过对时域响应及相关数据进行分析可知,两种控制方式都能有效改善汽车悬架的动力学性能。虽然在脉冲路面输入激励下,PID主动控制比反馈线性化LQR主动控制能更有效减小悬架动挠度,但是对车身加速度和轮胎动载荷控制效果不如反馈线性化LQR主动控制。这是因为利用微分几何法可以将非线性分数阶悬架系统精确线性化,即利用反馈抵消系统中非线性项和分数阶项。线性化后的悬架系统采用LQR控制能够更好的抑制悬架的振动、降低悬架的动变形和减少路面对悬架的冲击。
5 结 论
本文针对比整数阶模型更加能够准确描述实际悬架系统的非线性分数阶悬架模型,用Oustaloup滤波器算法对分数阶项进行处理,采用微分几何法将系统进行反馈线性化,并设计了LQR控制器对系统进行主动控制,分别在路面随机激励和脉冲激励下进行研究,仿真结果表明,该方法相对于PID主动控制算法和被动控制,控制效果明显提高。本文为含分数阶微分项非线性汽车悬架的控制提供了简单有效的思路。
