空心圆柱形金属橡胶非成型向阻尼特性理论研究及参数识别

张 彬， 任志英， 白鸿柏， 陈其胜， 路纯红

(1.福州大学 机械工程及自动化学院 金属橡胶工程研究中心， 福州 350108;2.河北工业职业技术学院 汽车工程系，石家庄 050001)

金属橡胶是一种弹性多孔材料，由金属丝加工成螺旋卷，再经过特殊的缠绕编织工艺制成毛坯，通过冷冲压成型。因其具备类似橡胶的弹性和阻尼性能而被称为金属橡胶。由于金属橡胶原材料是金属丝，与橡胶相比，金属橡胶具有真空中不挥发，耐高/低温，耐腐蚀，不惧怕辐射，疲劳老化寿命长，可长期保存等特点[1-2]，故近年来金属橡胶被广泛应用于减振领域。经研究，金属橡胶的刚度特性和阻尼特性均具有较大的历史依赖性，随着变形的增加，其性能不断变化，具有强烈的非线性特征[3-7]，这导致对金属橡胶的动力学分析过程十分复杂。目前来看，对金属橡胶类隔振系统的方法大多是将非线性恢复力进行分解，而后对各个分解力分别进行表示，最后通过不同算法对模型进行参数识别。张玲凌等[8]用参数分离法建立了金属橡胶阻尼器力学模型，利用二维拉格朗日插值法和人工神经网络法对模型参数进行了识别，取得了良好的识别精度；闫辉等[9]将利用双折线模型来描述金属橡胶隔振器模型，用能量法和最小二乘法对模型进行参数识别，最终取得了较好的精度；李冬伟等[10]根据金属橡胶材料的作用机理提出了一种非对称弹性黏性阻尼双折线恢复力模型，经傅里叶级数展开后设计了一种分离参数算法对模型进行识别；路纯红等[11]设计了金属橡胶/橡胶叠层耗能装置，在试验结果基础上建立动力学模型，并利用迟滞回线分解识别算法对模型进行识别；李玉龙等[12]设计了串联金属橡胶减振系统，借鉴双折线模型建立了系统动力学模型，利用小生境遗传算法进行了参数识别。以上成果对金属橡胶减振设计具有一定的参考意义，不过现有的研究都是局限于金属橡胶的成型方向。

由金属橡胶特殊的成型工艺可知金属橡胶非成型方向的减振特性必然不同于其成型方向。而目前，对于金属橡胶非成型方向的研究成果可以说凤毛麟角。笔者所了解到的关于非成型方向的研究成果由曹凤利等[13]从微观角度着手，研究了金属橡胶非成型方向的变形机制，最终结合螺旋卷弹性变形特征和金属橡胶内部摩擦力接触点分布规律建立了非成型方向的力学模型；吴荣平等[14]通过实验对比了部分金属橡胶参数对其径向力学性能的影响，从宏观角度建立了金属橡胶力学模型，该模型同样较好地描述金属橡胶的载荷-变形关系。已有的研究成果都局限于静力学方面，对金属橡胶非成型方向动态阻尼性能方面的研究较少。事实上，工程实际中，金属橡胶更多是作为减振材料，需要发挥其阻尼耗能特性。对其各个方向的阻尼性能进行全面的研究是必要的。

本文以空心圆柱形金属橡胶为研究对象，深入研究了金属橡胶非成型方向的阻尼特性。先通过实验对比了成型方向和非成型方向的压缩机理，进一步研究了金属橡胶密度和加载频率变化时，对应的非成型方向的阻尼特性的变化规律。基于试验结果利用参数分离法建立了阻尼特性模型，用最小二乘法对模型参数进行了识别。经验证，所建立模型具有良好的精度。本文研究内容对推广金属橡胶减振应用设计有重要意义。

1 制备及试验方法

1.1 金属橡胶制备

通过传统的制备工艺制备的四种密度的金属橡胶如图1所示。金属橡胶外径30 mm，内径10 mm，高30 mm。试件原材料选用了牌号为304(06Cr19Ni10)的奥氏体不锈钢丝，丝径为0.3 mm。

图1 不同密度的金属橡胶Fig.1 Metal rubber of different densities

1.2 试验设备及试验方法

试验采用长春机械科学研究所SDS-200高低温动静材料试验机对金属橡胶进行正弦加载以及响应数据采集。试验机最大工作载荷200 kN，试验频率为0.01～40 Hz。试验设备及原理如图2所示。

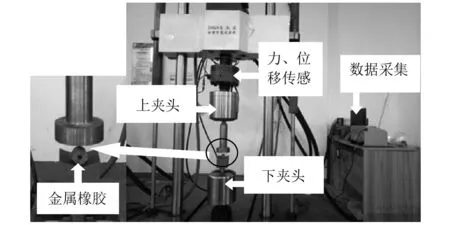
图2 动静材料试验机Fig.2 Dynamic and static material testing machine

2 金属橡胶非成型向压缩机理

为比较非成型方向与成型方向的动态特性，首先对ρ=2.5 g/cm3的金属橡胶进行加载试验，得到成型方向和非成型方向的迟滞回线如图3所示。从图中可以看出金属橡胶非成型方向和成型方向的迟滞回线走向不同，说明两个方向的力学特性并不一致。非成型方向的迟滞回线整体斜率明显大于成型方向，即动态平均刚度更大，说明金属橡胶是一种各向异性材料。

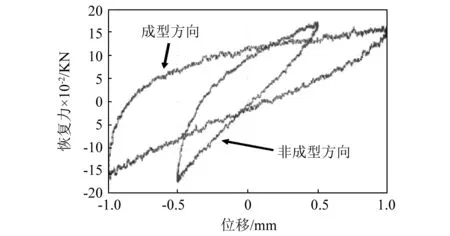
图3 金属橡胶不同加载方向的迟滞回线Fig.3 Hysteresis loop of metal rubber in different loading direction

出现这种现象是因为成型后的金属橡胶内部结构可视为众多的金属丝螺旋卷相互勾连叠加堆砌在一起，其中大部分的螺旋卷平行于与压力成型方向相垂直的法向面。在外力载荷的作用下，金属丝产生类似曲梁的弯曲变形。在金属橡胶成型方向上产生的变形类似于螺旋弹簧受到轴向力时产生的变形，在成型方向上层叠的金属丝可视为相互串联累加；而在非成型方向上，产生的变形类似螺旋弹簧非承载方向上承受径向载荷时产生的变形，此时金属丝的弯曲变形所产生的反力更大，且相互层叠、串联的金属丝可视为并联形式，故其非成型方向上所产生的弹性力更大。下面进一步研究非成型方向的动态特性。

3 试验过程及结果分析

3.1 阻尼特性评价指标

阻尼是用来表征系统受激后快速恢复到受激前状态的一种能力。阻尼越大，系统所需的恢复时间越短。表征材料阻尼性能的参量有很多，最常用的度量参量有阻尼比ψ、相位差角正切值tanφ、损耗因子η、对数衰减率δ和品质因子的倒数Q-1。由于金属橡胶的非线性迟滞特性，故无法使用一些基于线性原理的测试方法。

迟滞回线体现了材料的阻尼特性，其包围的面积与阻尼耗能有直接关系。本文对金属橡胶施加正弦位移，利用实测恢复力响应信号，直接计算一个周期内的耗能与最大弹性势能，进而得到金属橡胶的等效耗能因子。

试验机对金属橡胶施加位移可表示为

X=X0cos(ωt+α)

(1)

式中:α为初始相位;X0为试验输入的振幅；ω为加载频率。

一个周期内，金属橡胶试件所耗损的能量ΔW可离散化[15]表示为

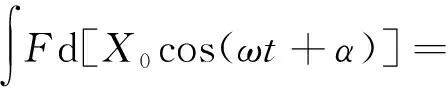
(2)

式中：N为一个周期内的离散点数量，N=f0/f,f0为系统采样频率，f0=2 500 Hz;f为加载频率。

材料所储存的最大弹性势能W可表示为

(3)

式中：Fmax,Fmin为采样系统中采集的恢复力的最大值与最小值；K为动态平均刚度，其表达式为

(4)

损耗因子η为系统中损耗的能量与最大弹性能的比值。通过式(5)可以计算得出等效损耗因子

(5)

3.2 试验过程

为了避免加载过程中工件脱离工装的情况，试验前对工件进行预紧。假定预紧后的位置为正弦位移加载的平衡位置，对试件施加正弦激励。应用数据采集装置对力、位移信号进行采样，其中采样频率f0=2 500 Hz。试验数据处理中，考虑将正弦位移中点作为坐标原点，恢复力为上下位移加载过程中的实测值，未加入预紧力的影响。本文研究了加载频率和金属橡胶密度对金属橡胶非成型向阻尼特性的影响。具体试验参数如表1所示。

表1 单因素控制试验参数Tab.1 Single factor control test parameters

3.3 试验结果分析

3.3.1 不同加载频率对阻尼特性的影响

图4可知不同加载频率所形成的金属橡胶迟滞回线变化较小，说明在不同频率的激励下，金属橡胶元件的阻尼性能相差较小,金属橡胶的非成型向具有相对稳定阻尼性能。

图4 不同加载频率下迟滞回线Fig.4 Hysteresis loop at different loading frequencies

图5可以反映材料的实际变化情况。密度为2.5 g/cm3的金属橡胶的动态耗能变化较小，动态平均刚度有下降的趋势。最大弹性势能与动态平均刚度正相关。结合式(5)，动态平均刚度的变化幅度较大导致损耗因子呈现上升趋势。密度为3.5 g/cm3的金属橡胶耗能与动态平均刚度都略微提高，其中动态平均刚度的变化幅度相对较大，也即最大弹性势能变化幅度较大，这导致损耗因子呈现一个微小的下降趋势。

图5 不同频率下参数变化曲线Fig.5 Parameter change curves at different frequencies

3.3.2 不同密度对阻尼特性的影响

由图6可知滞环面积随试件密度增大而增大，即密度大的金属橡胶绝对耗能能力越强。

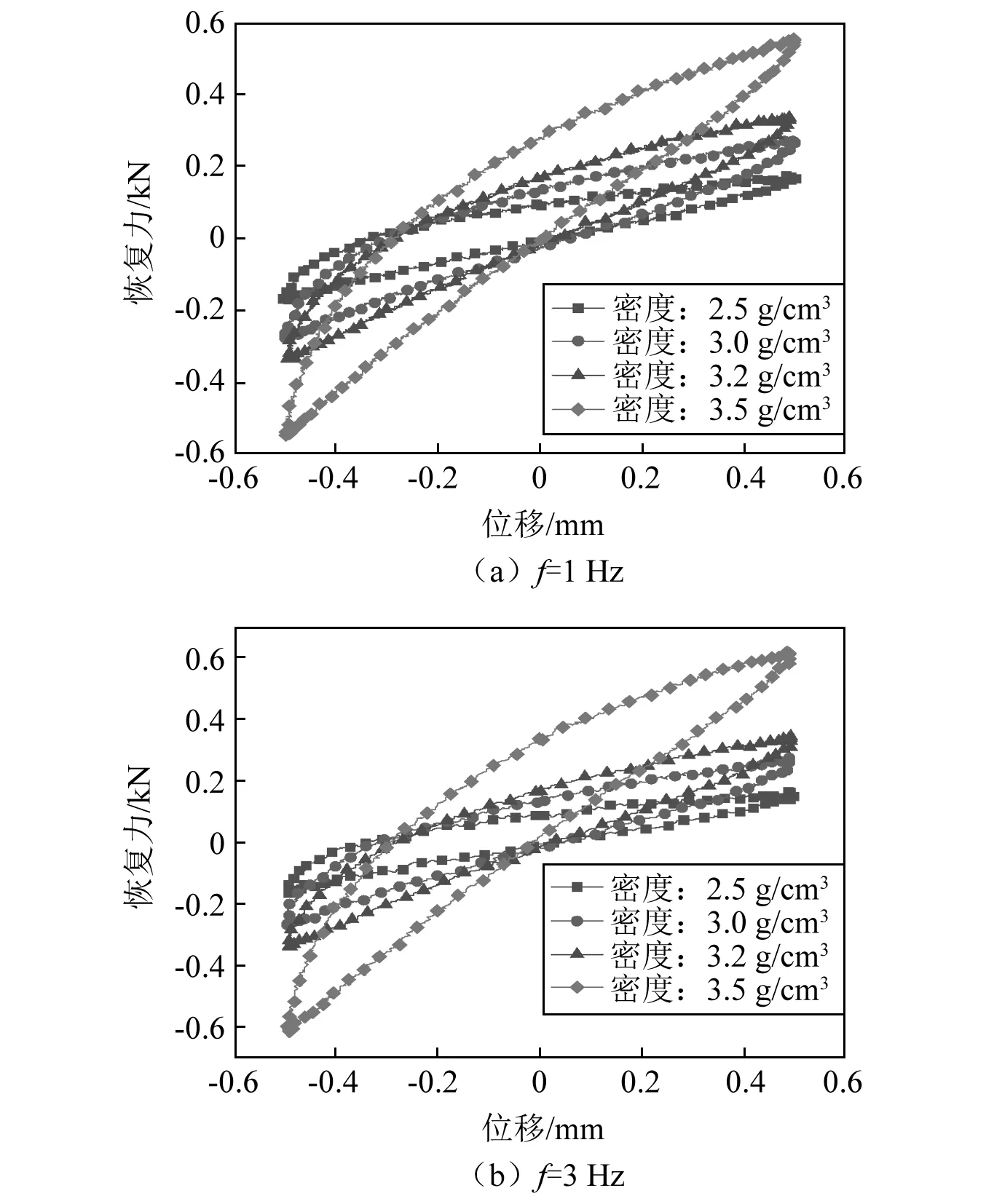
图6 不同密度下迟滞曲线Fig.6 Hysteresis loop at different densities

由图7可看出损耗因子的变化随试件密度增加呈下降趋势。随着密度增加，动态平均刚度增大，导致最大弹性势能的增大。同时绝对耗能也随着密度的增大而增大。但最大弹性势能的增加速度相较于绝对耗能的增加速度更快，由式(5)得损耗因子呈下降趋势。

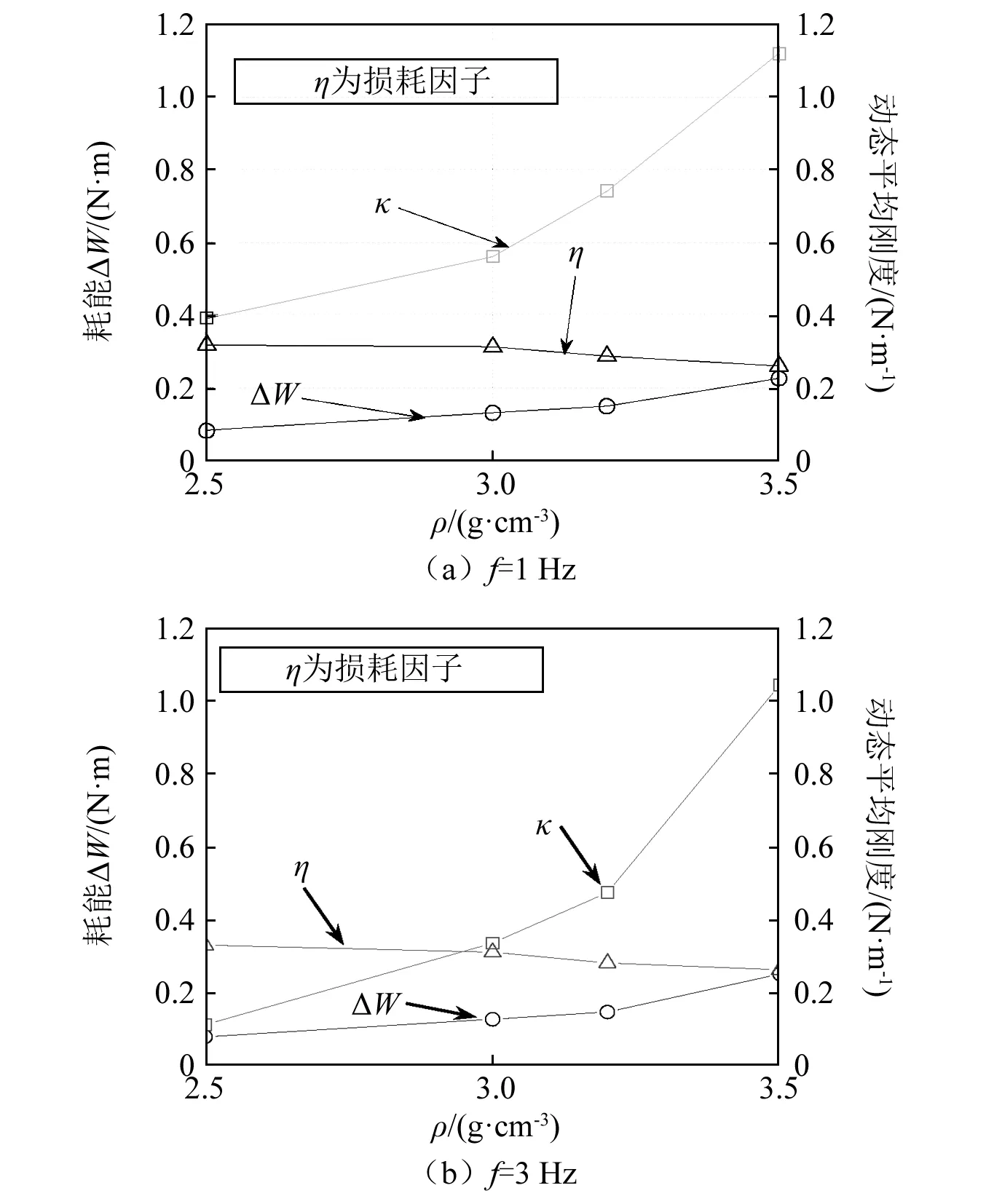
图7 不同密度下参数变化曲线Fig.7 Parameter variation curves under different densities

4 非成型方向金属橡胶材料阻尼模型的建立及识别方法

实际应用中，金属橡胶通常承受的是动态变化载荷，其动态力学性能会直接影响应用效果。由于迟滞特性的存在，其恢复力与位移变量并非是一一对应关系，故有必要建立其力学特性与参数之间的联系。此处建立了金属橡胶非成型方向的阻尼模型来表征阻尼特性随密度和频率的变化关系，并基于实验数据进行参数识别。

4.1 迟滞模型建立

图8(a)所示为实测的金属橡胶工件的迟滞回线。所测得的迟滞回线为非对称回线，在工程上，金属橡胶常以对称形式布置。故将试验数据去除初始压力后，取上半支曲线进行曲线拟合。重构后的金属橡胶迟滞回线如图8(b)所示。下面借助重构后的曲线进行建模和参数识别。

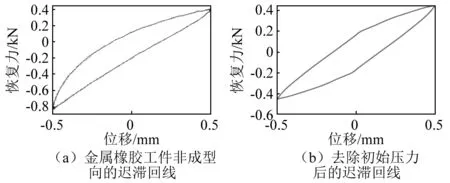
图8 金属橡胶非成型方向迟滞回线Fig.8 Hysteretic loop in non-forming direction of metal rubber

将上、下半支迟滞回线用幂函数多项式表述为

(6)

(7)

式中，αi为多项式系数。

若将两式的奇、偶次项分开，可进一步表示为

(8)

(9)

这样，式(8)、式(9)可统一写为

(10)

(11)

式中，sgn为符号函数。经处理后迟滞回线可分解为非线性弹性恢复力Fk和非线性阻尼恢复力Fc两部分。一般情况下忽略三次以上高次弹性恢复力可得

Fk{x(t)}=k1x+k3x3

(12)

k1=a1k3=a2

(13)

引入指数形式来描述非线性阻尼恢复力

(14)

最终得到恢复力数学模型为

(15)

4.2 参数识别

4.2.1 刚度系数

金属橡胶的动态平均刚度受到密度的影响较为明显，故本节识别出的刚度系数考虑密度为基础变量，并对其进行识别。采用第3章中的数据结果作为基础，通过提取某工况下的实验数据，采用最小二乘法对迟滞回线进行三阶多项式拟合即可得到刚度系数(k1，k3)。各阶刚度系数随密度变化的曲线如图9所示。

图9 刚度系数随密度的变化曲线Fig.9 Variation curve of stiffness coefficient with density

这里选用幂函数多项式拟合其随密度变化曲线

(16)

(17)

式中，a0,a1,a2,a3,b0,b1,b2,b3为待识别参数。

根据拟合识别得到的各个密度下的刚度系数k1,k3，用最小二乘法分别对二式进行多项式拟合，即可得到待定参数的识别结果，将其代入式(16)与式(17)可得

0.249 9ρ3

(19)

4.2.2 阻尼系数

(20)

从试验测得的总迟滞恢复力采样数据gn(i)中减去Fk(xi)，即可得到各个采样点的非线性阻尼力

(21)

据式(14)表示的阻尼模型，采用最小二乘法即可识别出阻尼系数c及阻尼成分因子α。

通过对不同频率及密度条件的试验结果进行参数识别，阻尼系数c(ρ,f)识别结果如表2所示。绘制阻尼系数随频率及密度变化的空间曲面，如图10(a)所示。阻尼系数与频率及密度的变化关系较为复杂，为建立阻尼系数与频率及密度间的联系，采用幂函数的形式，对其进行多项式拟合。拟合结果可用和方差(sum of the squared errors，SSE)与确定系数R-square表示。和方差SSE表示该拟合数据和原始数据对应点的误差的平方和，SSE越接近于0，说明拟合条件越好；确定系数是通过数据的变化来表征拟合结果的好坏，其正常取值为[0,1]，其数值越接近1，表明拟合结果越好。阻尼系数c(ρ,f)的多项式拟合表达式为

表2 不同频率及密度条件下阻尼系数Tab.2 Damping coefficients at different frequencies and densities

5.75×10-2ρ2+4.06×10-2ρf+2.38×10-2f2+

8.95×10-3ρ3+3.1×10-3ρ2f-1.33×10-2ρf2-

4.33×10-4f3-2.2×10-3ρ3f+2.45×10-3ρ2f2-

2.33×10-4ρf3+7.29×10-5f4

(22)

其拟合后图形如图10(b)所示。拟合结果和方差SSE=8.2×10-6，确定系数R-square为0.964 9。

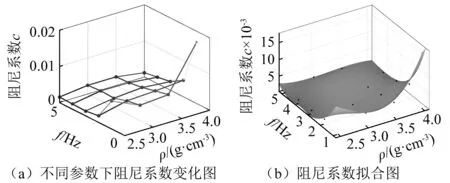
图10 不同频率及密度下阻尼系数变化图Fig.10 Changes of damping coefficient at different frequencies and densities

4.2.3 阻尼成分因子

通过对不同频率及密度条件的试验结果进行参数识别，阻尼系数α(ρ,f)识别结果如表3所示。

表3 不同频率及密度条件下阻尼成分因子Tab.3 Damping factor under different frequency and density conditions

阻尼成分因子的变化范围变化较小，图11为不同密度与频率下，阻尼系数变化图。此处多项式拟合表达式为

1.48f2-0.36ρ3-0.63ρ2f+0.52ρf2+0.14f3+0.14ρ3f-

9.60×10-2ρ2f2+1.54×10-2ρf3-1.46×10-2f4

(23)

图11 不同频率及密度下阻尼成分因子变化图Fig.11 Changes of damping component factor at different frequencies and densities

拟合结果和方差SSE=0.027 9，确定系数R-square为0.964 8。

4.3 模型验证

将式(16)中的待识别参数替换为各个对应参数的表达式(18)、式(19)、式(22)及式(23)，即可得到金属橡胶动态非线性模型。通过金属橡胶非线性模型可以估计出不同密度ρ和频率f的恢复力迟滞曲线。与实测后重构的金属橡胶迟滞回线对比如图12所示。拟合出的预估曲线与实测曲线之间的误差较小，说明了三次非线性弹性恢复力与与速度相关的高次非线性阻尼力的叠加可较合理的描述金属橡胶迟滞回线。同时也说明参数分离识别方法具有很好的工程精度。

图12 拟合线与去除初始压力后重构曲线对比Fig.12 Comparison of fitting line and reconstructed curve after removing initial pressure

5 结 论

(1)制备了不同密度的金属橡胶，利用材料试验机对其非成型方向进行不同频率的加载试验，并以等效损耗因子来表征阻尼能力。结果表明金属橡胶非成型方向的的阻尼性能在低频段受频率变化影响较小。随着密度的增加，金属橡胶非成型方向的损耗因子呈下降趋势。对常用的密度ρ=2.5 cm/g3的金属橡胶的不同成型方向进行了加载试验，由滞回曲线表明，金属橡胶非成型方向的动态刚度大于成型方向的动态刚度。

(2)为分析金属橡胶密度和加载频率变化时，对应的非成型方向阻尼特性的变化规律，基于试验结果利用参数分离法建立了阻尼特性的模型，并用最小二乘法对模型参数进行了识别。经验证，所建立模型具有良好的精度。