桩柱式桥台土-结构相互作用抗震性能研究

焦驰宇， 吴闰然， 龙佩恒， 鲁子明

(1.北京建筑大学 北京未来城市设计高精尖创新中心，北京 100044； 2.同济大学 土木工程防灾国家重点实验室，上海 200092；3.北京建筑大学 工程结构与新材料北京市高等学校工程研究中心，北京 100044； 4. 北京建筑大学 北京节能减排关键技术协同创新中心，北京 100044；5. 北京市首发高速公路建设管理有限责任公司，北京 100044)

国内外地震表明桥梁破坏受损严重，而其中桥台的震害往往容易被忽略。如图1所示，2008年汶川地震(M8.0)中，西南地区某跨河桥发生严重破坏，地震时主梁发生纵向滑移，桥台台身破坏并向河心倾斜，翼墙开裂，前墙几乎脱落，胸墙被主梁撞碎并被顶入路基50 cm以上[1]；1994年美国Northridge地震(M6.7)中，受损的桥梁中一半以上的桥梁出现了桥台震害。图2为一座10跨曲线箱梁桥，地震造成主梁与桥台碰撞、桥台侧墙破坏,主梁也因失去了桥台的支撑约束，而背离桥台移动了150 cm[2]。从上述可以看出，地震中土-桥台-上部结构相互作用是导致桥台破坏的主要原因。

图1 桥台胸墙撞碎(汶川地震，2008年)Fig.1 Abutment parapet smashed(Wenchuan earthquake,2008)

图2 桥台挡块破坏(Northridge地震，1994 年)Fig.2 Shear key failure of abutment(Northridge earthquake,1994)

国内外学者对影响桥台地震响应的因素进行了广泛的研究，Al-Homouda等[3]发现了重力式挡土结构在地震作用下沿高度方向存在放大效应并对其进行了分析研究。周晓岩等[4]通过数值模拟，得出结论为桥台顶部加速度放大系数在1.2～2.0。其次，由于土体的剪胀特性是土体特有的一种非线性变形特征，张培文等[5]先后提出了边坡稳定性系数和地基承载力随着土体剪胀角的增加而增大。何培勇等[6]提出对路基边坡稳定影响较大的因素也是土体的剪胀角。与此同时，考虑到大震作用下桥台与土体的接触关系可能发生改变，宿金成等[7]研究发现在高加速度地震波作用下，必须考虑土-结构的动力相互作用和接触非线性。刘书等[8]基于不同的数值模拟方法，对桥台与土体之间的接触条件以及接触面处的力学微分方程进行了探讨和研究。

现有的研究依然有许多不足。首先，以往研究虽然验证了桥台地震响应沿高度方向存在放大效应，但仍未系统阐明其规律。过去学者们曾探讨过台背填土的类型对桥台地震响应的影响，但未详细解释台后填土的剪胀特性对桥台抗震性能的影响。同时，以往研究在选择桥台与土体的接触模型时，通常考虑二者共用节点的模式，该方法对分析结果有不利的影响。针对这些不足，本文开展了以某立交匝道曲线桥为背景，建立实体模型的地震反应研究，对地震过程中桥台各单元的时程位移曲线进行监测，并探究了桥台高度、土体剪胀角度、土体与桥台接触截面模式三种影响因素对地震作用下桥台位移响应的影响。本文研究成果可为桥台结构的地震响应研究提供研究基础。

1 建立模型

1.1 工程背景

本文以某立交曲线匝道桥桥台为背景。该桥台为桩柱式桥台，桥台高度2.5 m，台顶宽度8.26 m，背墙厚0.4 m，台身底部1.4 m，桩径1.2 m，桥台侧面图如图3所示。

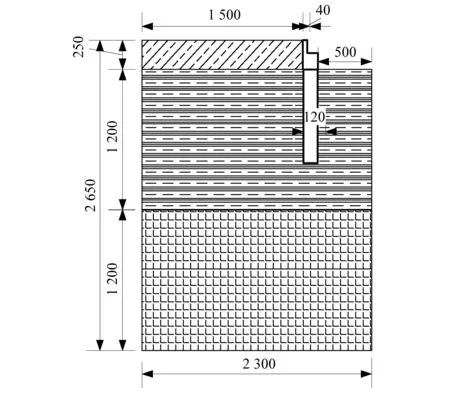
图3 桩柱式桥台模型剖面示意图(cm)Fig.3 Profile sketch of ribbed abutment model(cm)

1.2 数值模拟方法

为了更好的模拟顺桥向地震输入下土体与结构的相互作用，本文在ABAQUS有限元软件中建立了土体-桥台相互作用体系模型，如图4所示。模型长度取为桥台三倍，模型整体分为台身、桩基以及土体三个部件，均采用实体三维八节点(C3D8R)单元建立。

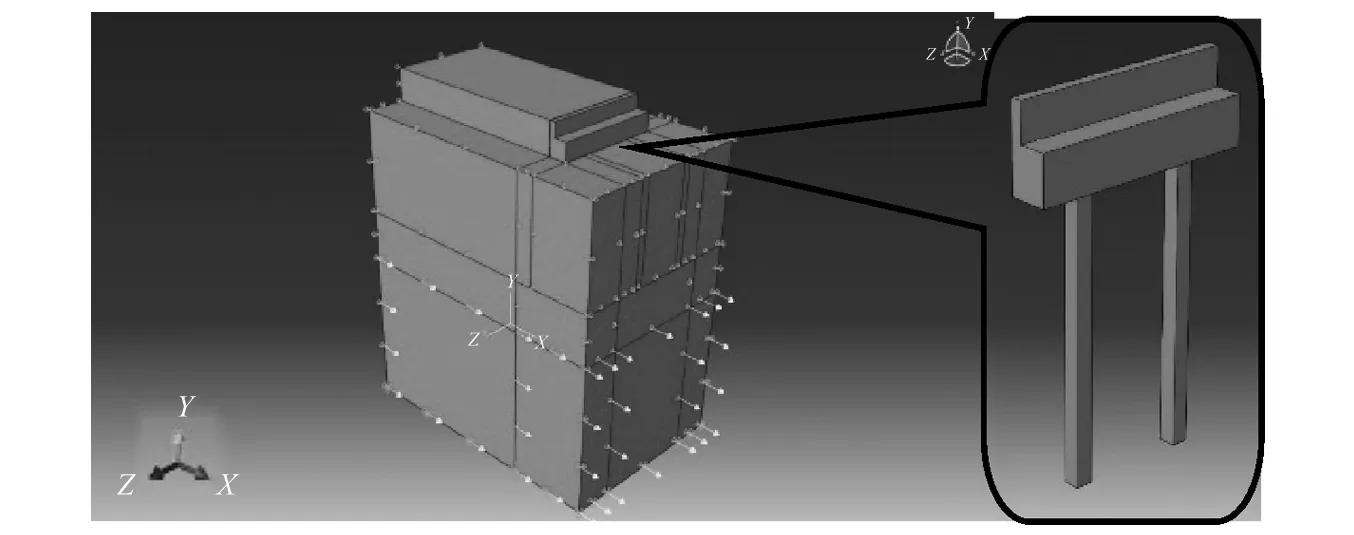
图4 土-桥台相互作用三维分析模型Fig.4 Analysis model of soil-abutment interaction

由于土体与桥台背墙是一对相互接触的表面，在ABAQUS的接触模拟中，需要在接触位置处设置接触对，本文模拟时选择面-面接触形式模拟接触对，并将一面设为主控面，一面设置为从属面，如图5所示(这里主从-面间隙为示意，计算时二者接触)。在主-从面之间设置法向与切向的接触属性来准确模拟接触面之间的力学行为。为能更加准确且高效地模拟土-桥台相互作用，对网格采用多尺度思想划分。在桥台台身及桩基处将网格细化，采用结构化网格划分，桥台网格尺寸为0.2 m，土体部分网格尺寸为0.6 m。计算分析中，土体网格与桥台网格之间的单元采用了接触单元，保证了二者位移的连续性。网格划分情况如图6所示。桥台、桩及土体物理参数如表1所示。

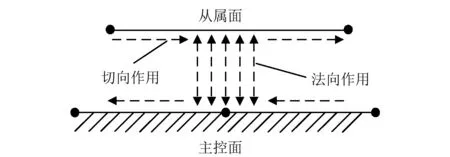
图5 面-面接触算法示意图Fig.5 Surface to surface contact method schematic diagram

图6 模型网格划分图Fig.6 Model meshing graph

表1 土体物理参数表Tab.1 Table of soil physical parameters

在桥台台背与土的位置、柱和土之间的位置设置有接触对，采用刚度较大的桥台为接触主控面，选择土体作为接触从属面。

接触面的法向作用模型也称为接触压力-过盈模式，其默认的模型为“硬”接触，对大部分接触问题来说，只有当两接触面之间压紧时，才会产生接触面间的法向行为，假设两接触面之间传递的法向压力为P，当两接触面之间存在间隙时，P=0，其接触压力与接触距离关系如图7所示。“硬”接触的接触面约束施加算法又有三种，分别为直接法、罚刚度法以及增广拉格朗日乘数法(augment lagrange method)。接触压力-过盈模型中除了“硬”接触外，还有“软”接触。“软”接触适用于接触面有一方或者单薄软面的模拟，如垫片，表面涂层等。

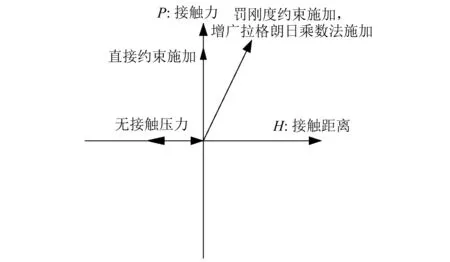
图7 接触压力与接触距离关系图Fig.7 Contact pressure and contact distance diagram

参考相关文献，综合考虑土体的材料性质、计算结果收敛速度，模型中使用“硬”接触模型中的罚刚度法模拟桥台与土体法向接触行为，其在软件中实现如下：土体与桥台背墙是相互接触的一对表面，在土体与桥台背墙之间设置接触对，以刚度较大的桥台作为主控面，土体为从属面，接触离散方式选择面-面接触进行离散，然后在接触对设置的正应力模式中选择“硬”接触模式，在约束算法模式中选择罚刚度法进行模拟，在罚刚度算法中需预设接触刚度k，k=f·E，其中f为0.1～10的系数，E为刚度较小材料的弹性模量，通常设f=1对计算结果收敛较好。土体与桥台切向接触行为方面，同样是面-面接触离散方式，并且选择罚刚度计算法，将土体与混凝土接触面摩擦因数设为0.55，不设置最大剪应力值，其余参数根据选择的材料性质填入即可。

接触面切向作用模型方面，采用的时库伦摩擦模型，三维模型中将两接触面之间的接触剪应力分为两个正交分量τ1和τ2，在ABAQUS中将二者合并为“等效剪应力”τeq，具体如图8所示。

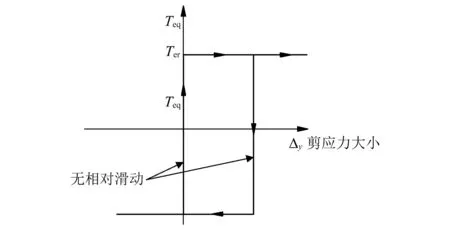
图8 库伦摩擦模型Fig.8 Coulomb friction model

图8横坐标代表相对滑移量，纵坐标代表剪应力大小。τcr为发生滑动的临界剪应力。

图8中等效剪应力

(1)

不发生滑移时

(2)

发生滑移时

(3)

本文选取三倍顺桥向桥台范围作为桥台与土体相互作用的影响范围，并基于刚性基底假设进行分析。在ABAQUS中设置模型侧向边界的法向位移为零，竖向边界的法向位移也为零，如图9所示。

图9 模型边界条件模拟情况图τeqFig.9 Model boundary condition simulation diagram τeq

1.3 地震波的输入

该桥地处III类场地，烈度为8度。利用罕遇地震下规范反应谱生成三条人工地震波，后续计算中选取三条地震波效应最大者进行时程分析，加速度时程曲线如图10所示。其峰值为4.066 m/s2(0.37g)。地震波输入方向取为该曲线桥两桥台的连线方向，即桥台边缘的垂线方向[9]。

图10 人工地震波加速度与时程曲线图Fig.10 Graph of acceleration time history curve of artificial ground motion

1.4 模型的可靠性

计算地震动土压力时常采用Mononobe-Okabe地震土压力理论(以下简称为M-O理论)。M-O理论是基于库伦土压力理论的基础并考虑地震惯性力后得到的地震土压力合力计算公式。假设作用于挡土墙背上的地震土压力是由墙后填土在极限平衡状态下出现的滑动楔体产生，如图11所示。在地震动作用下，身为刚体的滑动楔体整体的加速度相同。由作用于该滑动楔体上力的平衡条件可以得到作用于整个结构上的地震土压力合力。在地面为水平面、墙背为垂直面的情况下，M-O理论给出的地震土压力合力为

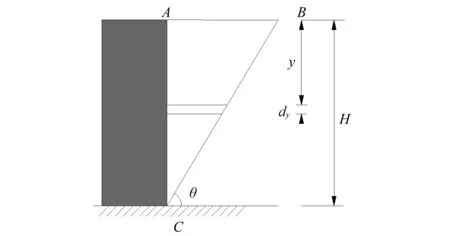
图11 滑动楔体示意图Fig.11 Schematic diagram of sliding wedge

(4)

其中，

(5)

式中：P1为地震土压力合力；γ为土的容重；H为桥台背墙高度；θ为墙体的水平夹角；h为墙后土体内摩擦角；W为墙后土体与墙背之间的摩擦角；j为地震角；kh，kv分别为水平、竖向地震加速度与重力加速度的比值。

若从图11的滑动楔体深度y处，取一薄片单元，其厚度为dy，薄片单元示意图如图12所示。

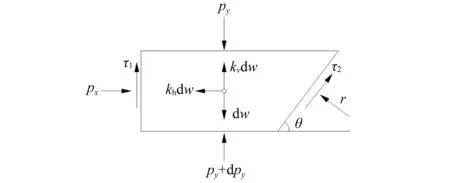
图12 薄片单元分析示意图Fig.12 Analysis sketch of sheet element

由作用在薄片单元上的水平力平衡条件可得

px+τ2cotθ-r-khγ(H-y)cotθ=0

(6)

由作用在薄片单元上的竖向力平衡条件可得

令

px=Kpy；τ1=pxtanW；τ2=rtanh

(8)

将式(8)代入式(6)和式(7)，可得

式中：px为薄片单元水平反力；py为薄片单元体顶面竖向应力；γ为垂直与滑动面的反力；τ1,τ2分别为对应滑动面的摩擦力；K为土侧压力系数。

令

(10)

则式(9)可得解为

(11)

又由px=Kpy，作用与桥台背墙的水平压力为

(12)

由式(6)和式(8)可得

(13)

可对整个滑动楔体进行力矩平衡，对图11中C点取矩，可得式(14)。

(14)

由于px，py，r均已知，由式(14)可得地震作用下土侧压力系数K为

(15)

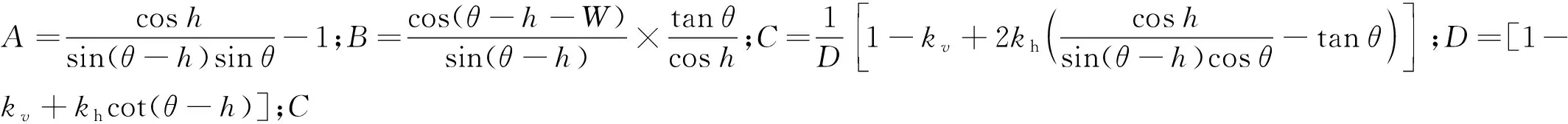
则土压力合力作用点距墙底的距离可表示为

(16)

由式(16)可以看出，当地震动峰值加速度较小时，kv和kh接近于零，式(16)中BK接近为1，地震土压力合力作用点高度Hp大约在距离背墙底部1/3高处。随着地震峰值加速度的增大，地震加速度与重力加速度的比值将发生改变，导致kh,kv数值增大，BK值大于1，从而由式(16)可得出，随着地震峰值加速度的增大，地震动土压力合力作用点会有所上移，大约在距离背墙底部1/3～1/2高度处[10]。

在本文模型中，施加了地震动荷载后进行时程动力分析计算。得到如图13所示桥台背墙与土体接触应力的应力云图。从图中可以看出，当地震动峰值加速度为0.37g时，桥台背墙出现两个应力最大值区域，位置大约在桥台背墙距底部1/3高处。随着地震动峰值最大值的逐渐提高，这两个接触应力最大值区域会逐渐上移。从图13(c)可以看出，当地震动峰值增加到0.75g时，接触应力最大值出现在大约距底部1/2处。这与M-O理论所计算的地震土压力作用点位置在背墙中点至1/3处基本一致。相关文献也对挡土墙的土压力合力作用点随着地震加速度峰值的变化而改变的规律进行了总结，文献[11]得出在0.2g地震峰值加速度作用下，土压力合力作用点位于距挡土墙墙脚0.333高度处，随着加速度峰值增大，合力作用点位置有所提高，在0.8g地震峰值加速度下提高到距墙脚0.458高度处。与本文得出结论类似，进一步验证了采用ABAQUS建立的土-桥台相互作用下的桥台地震响应模型的可靠性。

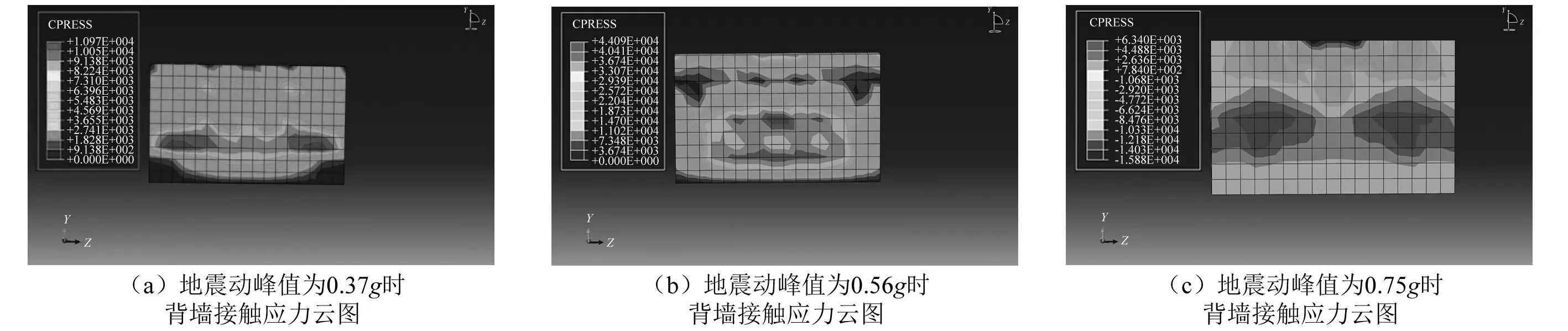
图13 桥台背墙接触应力云图Fig.13 Contact stress nephogram of back wall

2 桩柱式桥台地震反应规律

2.1 桥台位移

为了研究桥台在地震过程中的位移响应特性，对地震过程中桩柱桥台背墙自底部向上各单元的时程位移曲线进行监测。并探究以下三个影响因素对地震作用下桥台位移响应的影响：①桥台高度；②土体剪胀角的取值；③土体与桥台接触界面。下文将从这几个方面展开论述。

2.1.1 不同桥台高度下桥台地震位移

根据以往研究可知，桥台地震加速度峰值沿桥台高度方向上存在放大效应。为了解不同桥台高度对桥台位移的影响，本文采用桩柱式桥台实体模型，并选取三种不同桥台高度，即2.5 m,3.5 m和5.0 m，分别对这三种不同桥台高度的模型施加三条不同大小地震动峰值的地震荷载，通过对比分析研究桥台高度对桥台位移的影响。对比模型汇总表格，如表2所示。

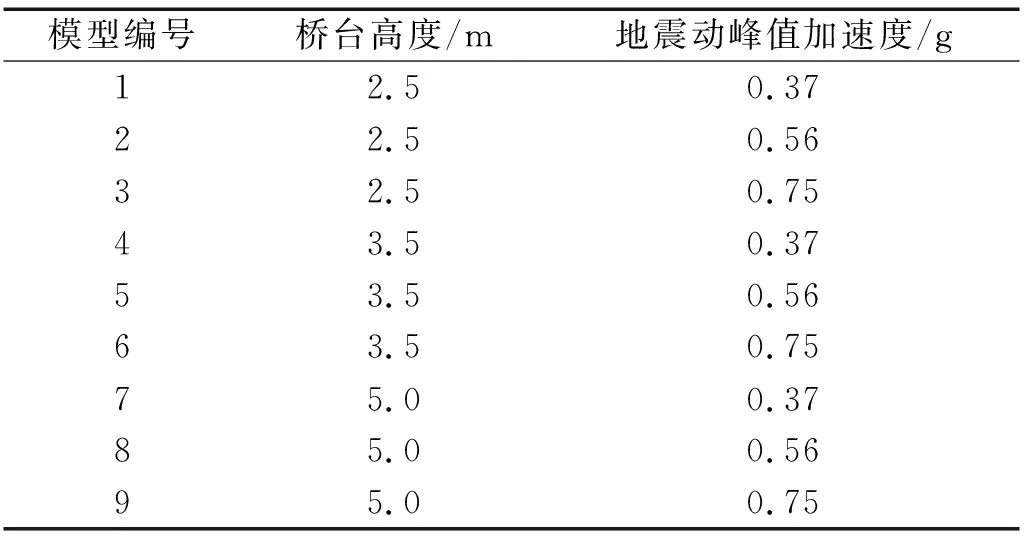
表2 不同桥台高度对比模型汇总Tab.2 Summary of contrast models for different abutment heights

三种桥台高度的桥台背墙在不同大小地震动峰值加速度下位移放大系数对比图如图14所示。图中横坐标代表相对高度(所测位移点的高度与背墙总高度之比)，即0代表背墙底部，1代表背墙顶部。纵坐标代表相应高度处的位移与背墙底部位移的比值，即位移的放大系数。在总结桥台背墙地震反应位移沿高度的分布规律时，应着重关注两个特征，一是背墙顶部的放大系数，即放大系数的最大值，与桥台总高度的关系；二是桥台背墙位移沿高度放大的速率与地震动峰值加速度大小的关系。

由放大系数对比图可见，桥台背墙位移沿高度的放大系数总体呈线性增加的趋势。如图14(b)所示，当地震峰值加速度为0.56g时，5 m高的桥台背墙位移放大系数为2.14，高于2.5 m高的桥台背墙位移放大系数20.22%。观察图14(a)、图14(b)、图14(c)也可发现，桥台高度越大，地震加速度峰值越大，位移放大系数随高度增加趋势越显著，由原来的线性增加变为接近于幂指数增加。

由图14(d)、图14(e)、图14(f)可见，同一高度的桥台背墙位移放大系数随着地震峰值加速度的增加而增加。但随着桥台高度的增加，高度较低处位移放大系数的在不同大小地震峰值加速度下的增加速率有所降低。这是因为虽然桥台整体高度在增加，但是由于上部结构高度一定，导致台身的高度也随之增加，这就会使桥台埋在土体以下的部分增加，土体对于桥台的约束作用加强，进而降低桥台的位移。

2.1.2 不同土体剪胀角下桥台地震位移

一般而言，在地震过程中，剪胀角会影响土体在剪切屈服过程中的体积变化，而且在土体的真实屈服过程中，土体的体积也是变化的。以往学者提出了岩土材料在非关联流动法则下剪胀角取值应为土体内摩擦角φ的一半[12]，在土-桥台相互作用体系当中，土体的体积变化规律对桥台在地震作用下的位移影响是我们所应关注的。图15为土体的剪胀角分别取φ/2 和0时，桥台顶部位移对比图。由图可知，土体剪胀角为零时与土体剪胀角取土体内摩擦角的一半时桥台顶部位移峰值相差不大。而整个地震过程中，两种不同剪胀角取值得模型桥台顶部位移也相差无几。说明土体剪胀角在土-桥台体系中对于桥台的地震位移响应影响不大。分析原因主要是土-桥台体系为弱接触体系，且二者材料属性相差较大，土体体积的变化对桥台地震位移响应影响较小。

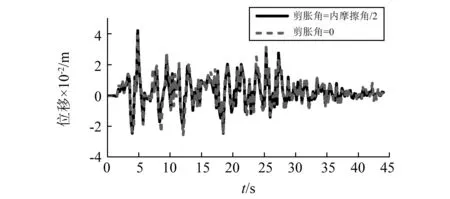
图15 不同剪胀角取值桥台顶部位移时程对比图Fig.15 Time-history contrast diagram of bridge abutment top with different shear expansion angles

2.1.3 土体与桥台接触界面对桥台地震位移

在土体与桥台相互作用的桥台动力有限元分析中，由于在小地震中桥台与土体之间不发生分离，土体与桥台的接触大多采用材料变形完全协调的假定，土单元与结构单元共用节点。然而桥梁在强震作用下，土体与结构之间的变形不耦合，土体与结构的接触面上有法向分离和切向滑移的现象。本文采用将土体与桥台接触界面为绑定的方式来模拟小震作用下，土体与结构变形完全协调情况下二者之间的接触；采用将土体与桥台之间设置法向接触和切向接触的方式来模拟强震作用下桥台与土体中存在变形不耦合的情况。对两种模型施加地震峰值加速度为0.75g的地振动荷载并进行计算分析，得到如图16所示的两种情况下桥台顶部位移时程对比图。

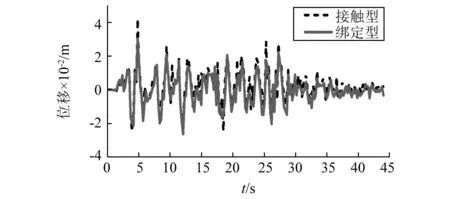
图16 两种接触情况的桥台顶部位移时程对比图Fig.16 Time-history contrast diagram of abutment top in two conditions

由图16可以发现，将桥台与土体采用绑定的方式连接在一定程度上缩小了桥台顶部位移响应。采用绑定连接方式的模型桥台顶部位移最大值比采用设置法向接触与切向接触连接方式的模型桥台顶部位移最大值小15%左右。由以上分析可知，采用将土体与桥台绑定的方式模拟二者之间的接触作用对于桥台的抗震计算是有风险的。

2.2 桥台压力

地震作用下，桥台的应力分布规律及土压力响应是桥梁设计人员所关心的重要设计依据。桥台在地震作用下产生过大的永久变形的重要原因之一是受到土体过大的推力作用。在地震过程中，台后土压力也是随机波动的，在土体的振动过程中所产生的动土压力有可能比静土压力大几倍，但是由于这种过大的地震作用持续时间较短，因此并不会立即使桥台破坏，而是逐渐增加桥台永久位移。如图17所示为桩柱式桥台在不同大小地震峰值加速度的地震作用下背墙土压力合力作用点(距桥台底部1/3)处的台背土压力时程曲线。

图17 桩柱式桥台台背土压力时程曲线Fig.17 Time history curve of earth pressure on the back of pile abutment

随着地震动峰值加速度的增加，桥台背墙的土压力响应也随之增加。0.75g地震波作用下桥台背墙的土压力峰值比0.56g地震波作用下的背墙土压力峰值大13.16%，比0.37g地震波作用下背墙土压力峰值大48.41%。但是地震动结束后，土压力残余应力并不是与地震动峰值加速度大小成正比关系。除此之外，当地震动结束时三种地震波作用下桥台背墙土压力作用点处的土压力残余应力也不尽相同。当峰值加速度为0.56g时，残余应力最大；当峰值加速度为0.75g时，残余应力反而减小。造成这种现象的原因主要是随着地震动的增强，桥台所受土压力的增大，桥台背墙可能发生破坏，残余应力随之降低。

3 结 论

本文采用桥梁通用有限元分析软件ABAQUS建立土-桥台体系实体模型，并根据M-O地震土压力理论验证了土-桥台体系实体模型的可靠性。通过比对桩柱式桥台不同高度、土体剪胀角以及桥台-土接触条件等模型在地震作用下桥台地震响应发现：

(1)在地震作用下桥台的地震响应存在着放大效应，在地震作用下桥台背墙顶部位移会比桥台底部位移大，这个放大系数随着桥台总高度的增加而增加，但随着桥台高度的增加，高度较低处位移放大系数的在不同大小地震峰值加速度下的增加速率有所降低。

(2)由于土-桥台体系为弱接触体系，且二者材料属性相差较大，所以土体剪胀角在土-桥台体系中对于桥台的地震位移响应影响不大。桥台顶部地震响应在考虑桥台与土体不发生分离时比考虑桥台与土体分离的桥台顶部地震响应大，所以在进行桥台抗震设计时应准确模拟土体与桥台的接触界面状态。

(3)随着地震动峰值加速度的增加，桥台背墙的土压力响应也随之增加。并且随着地震动峰值加速度的增加，桥台残余应力也会随之增加。但当到达一定极限时随着地震动的增强，桥台所受土压力的增大，桥台背墙土压力合力作用点处可能发生破坏，残余应力就将不再增加。桥台在地震作用下极易发生破坏，在进行桥台抗震设计时应着重关注桥台背墙与台身连接处，采用局部加筋等方式加固桥台。