悬挂式单轨线路关键点处的振动特性研究

2021-02-26寇峻瑜余浩伟李忠继

振动与冲击 2021年4期

寇峻瑜，余浩伟，李忠继，谢毅

(1.中铁二院工程集团有限责任公司，成都 610031； 2.四川高新轨道交通产业技术研究院，成都 610031)

悬挂式单轨交通系统作为一种新型的轨道交通制式，近几年在国内受到了广泛关注[1]。悬挂式单轨车辆悬挂于轨道梁下方[2-3]，走行部采用橡胶轮胎，依靠走行轮和导向轮分别实现走行和导向功能，其曲线运行机理、轮轨间振动特性与传统制式的轮轨交通存在较大差别。

通常列车通过直线与曲线连接位置处时，由于线型不同，线路曲率发生突变，轮对与轨道之间的相互作用也会发生变化，产生的激扰一定程度上会恶化列车运行平稳性和旅客乘坐舒适性。杨久川等[4]建立高速车辆模型，对缓和曲线和竖曲线起、终点处振动情况进行研究，结果表明缓和曲线长度越短或竖曲线半径越小，振动响应幅值越大。针对速度为300 km/h的高速铁路线形参数的研究，李向国[5]指出增加夹直线和圆曲线长度对提升列车平稳性和旅客舒适性的效果甚微，这与文献[6]一致，而夹坡段长度对避免振动叠加现象有一定作用。王开云等[7]仿真分析了350 km/h高速铁路下不同坡度和夹坡段长度下的轮轨系统响应，发现车体竖向加速度对坡度参数不敏感而对夹坡段长度敏感，并以振动不叠加原理为依据提出夹坡段长度不应小于300 m。

鉴于悬挂式单轨的特殊运行机制，使得车辆与线路之间的动力响应特性会有所不同，尤其是线路各关键点处的动态响应。目前，针对悬挂式单轨线路参数的研究还比较匮乏，尤其是平、纵断面关键点处的振动特性研究，少有的文献主要基于振动不叠加原理及轨道梁制造、安装难度，采用理论分析手段计算得出夹直线与圆曲线、夹坡段长度取值[8-9]。

由于静力学条件下的分析尚不能真实体现车辆的实际振动特性[10-11]，有必要对车辆运行状态下的动态响应进行研究。因此，本文基于国内某车辆厂家研发的悬挂式单轨车辆，采用动力学仿真手段，对线路曲率转折点处的振动特性规律进行分析总结，以期为悬挂式单轨线路设计参数的确定提供参考。

1 悬挂式单轨车辆系统动力学模型

悬挂式单轨系统是一个典型的多刚体系统，由车体、悬吊装置、转向架和箱型轨道梁等组成[12-13]。整个转向架置于下部开口的轨道梁内，通过一可绕轨道梁左右摆动的中心销与摇枕相连，中心销两侧安装有抗摇摆减振器，如图1所示。同时，摇枕与车体之间还布置有横向减振器、垂向减振器和牵引拉杆等。

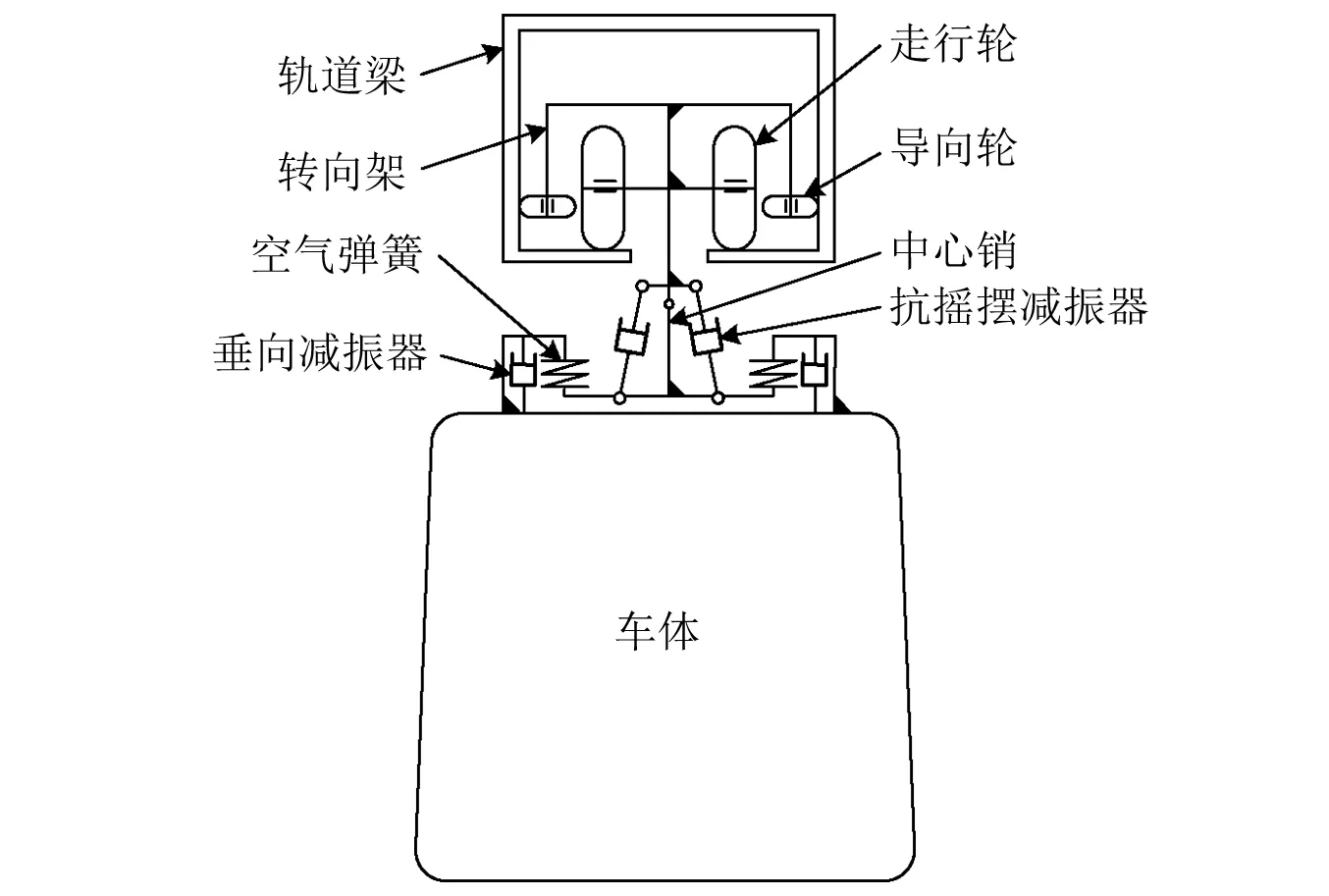
图1 悬挂式单轨车辆-轨道系统结构简图Fig.1 The structure diagram of suspended monorail vehicle-track system

采用动力学仿真软件Universal Mechanism(UM)建立悬挂式单轨车辆系统动力学模型，如图2所示。该模型仅考虑为单节车辆，包括车体、转向架构架、齿轮箱、摇枕、走行轮和导向轮等部件，均为刚体，整个模型共计60个自由度。模型中定义车辆前进方向为x方向，水平向左为y方向，垂直轨面向上为z方向。车辆部分主要技术参数取值如表1所示。

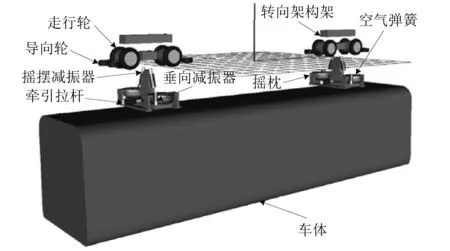
图2 悬挂式单轨车辆动力学模型Fig.2 The dynamica model of suspended monorail vehicle

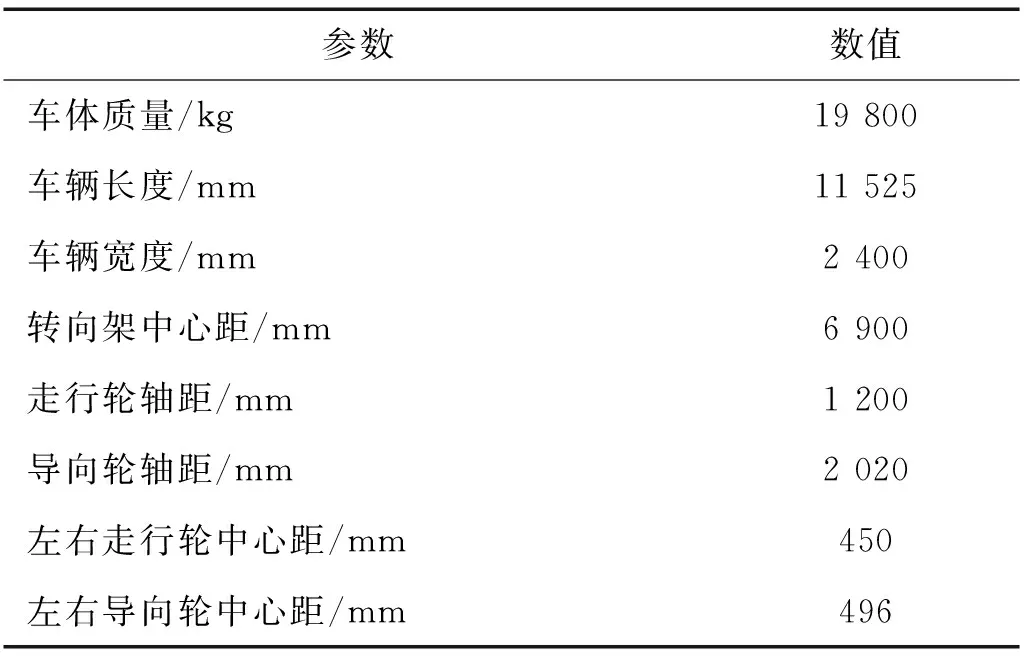
表1 车辆主要技术参数Tab.1 The major parameters of vehicle

考虑到实际的力学特征，悬挂式单轨系统中各减振器元件分别采用不同力元模型。横向减振器、垂向减振器和抗摇摆减振器采用Maxwell模型模拟其非线性特征，其阻尼力等于阻尼系数(常数)与车辆运行速度的乘积；空气弹簧和牵引拉杆则采用黏弹性力元模拟，其刚度和阻尼均线性化；走行轮和导向轮与轨道梁之间的接触关系采用Fiala轮胎模型进行模拟[14]，鉴于车辆运行过程中轮胎可能会瞬时脱离接触轨道梁，因此采用分段线性函数描述轮胎径向力Fz，其数学模型如式(1)所示，并且轮胎的建模主要考虑其径向特性[15]，轮胎径向刚度和阻尼系数均为常数(因轮胎变形量较小)。

(1)

式中：kz为实心橡胶轮胎径向刚度；Δr为轮胎径向挠度；dz为轮胎径向阻尼；VΔr为轮胎的径向变形率。

本文所建悬挂式单轨车辆系统动力学模型的拓扑关系如图3所示，可清晰快速地理解单轨系统各部件之间的连接关系和相对于坐标系的运动关系[16]，图中，α，β，γ分别表示绕x，y，z轴转动。

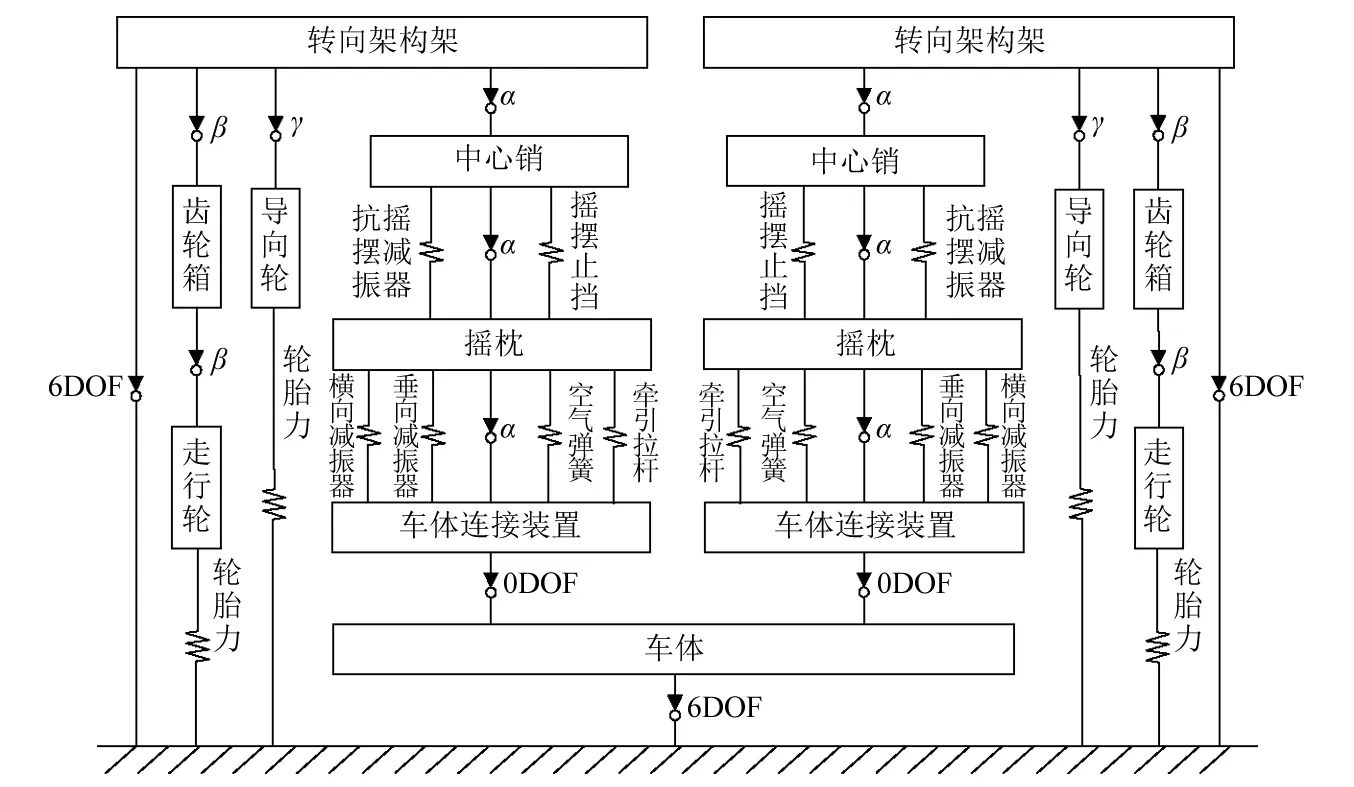
图3 悬挂式单轨车辆仿真模型拓扑结构图Fig.3 Topological diagram of simulation model of suspended monorail vehicle

2 线路关键点处的振动特性

悬挂式单轨车辆通过平、纵断面时，由于曲率变化，在线路线型转折点(如圆缓点、缓直点、竖曲线起终点等)处均会产生一定振动，并且重车工况下响应的幅值更大[17]，因此，下文主要以重载条件对线路各关键点处的振动特性规律进行研究。需说明，全文未考虑轨道梁不平顺的影响，是鉴于不平顺激励产生的随机振动会掩盖线路曲率变化点处的振动特性，无法准确判定是否存在振动叠加，因此本文主要研究车辆稳态通过曲线。

2.1 夹直线和圆曲线处的振动规律

表2列出了4种平面曲线工况，圆曲线半径和缓和曲线长度取一个适当的值，仅变化夹直线和圆曲线长度，并且夹直线两端的圆曲线方向相同，速度考虑为悬挂式单轨车辆的最高设计时速80 km/h，且整条线路不设置超高。为便于直观判断夹直线长度对振动叠加的影响，夹直线两端的圆曲线半径取相同值。

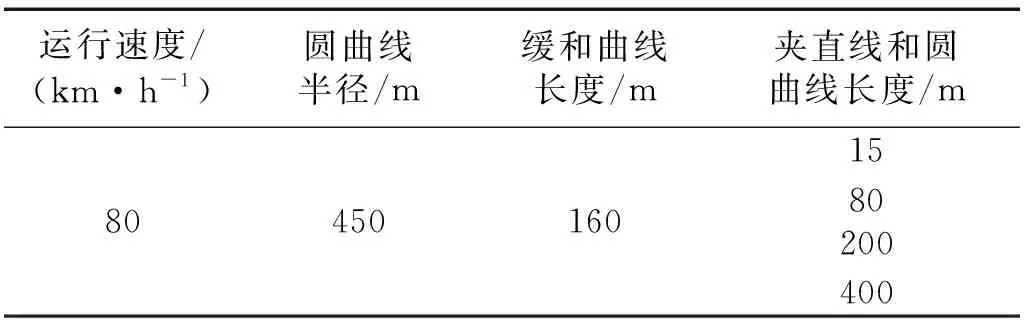
表2 夹直线和圆曲线长度动力计算线路参数Tab.2 Dynamic calculation line parameter of intermediate straight line and circular curve

悬挂式单轨车辆通过上述曲线工况时的动力学响应如图4所示。当夹直线和圆曲线长度LJ=400 m时，夹直线段处的振动衰减已基本完成。对比发现，由于存在振动叠加现象，当LJ=15 m,LJ=80 m时，第二段圆曲线处的横向加速度最大值(1.259 m/s2，1.235 m/s2)相比LJ=400 m的结果(1.203 m/s2)分别增大了4.7%，2.7%；当LJ=200 m时，第二段圆曲线处的横向加速度最大值(1.196 m/s2)相比LJ=400 m的结果减小了0.6%；并且走行轮垂向力和轮重减载率最大值的增、减幅也均较小。由此说明不同夹直线和圆曲线长度下的振动叠加效应不明显，即各动力学结果对夹直线和圆曲线长度不敏感。

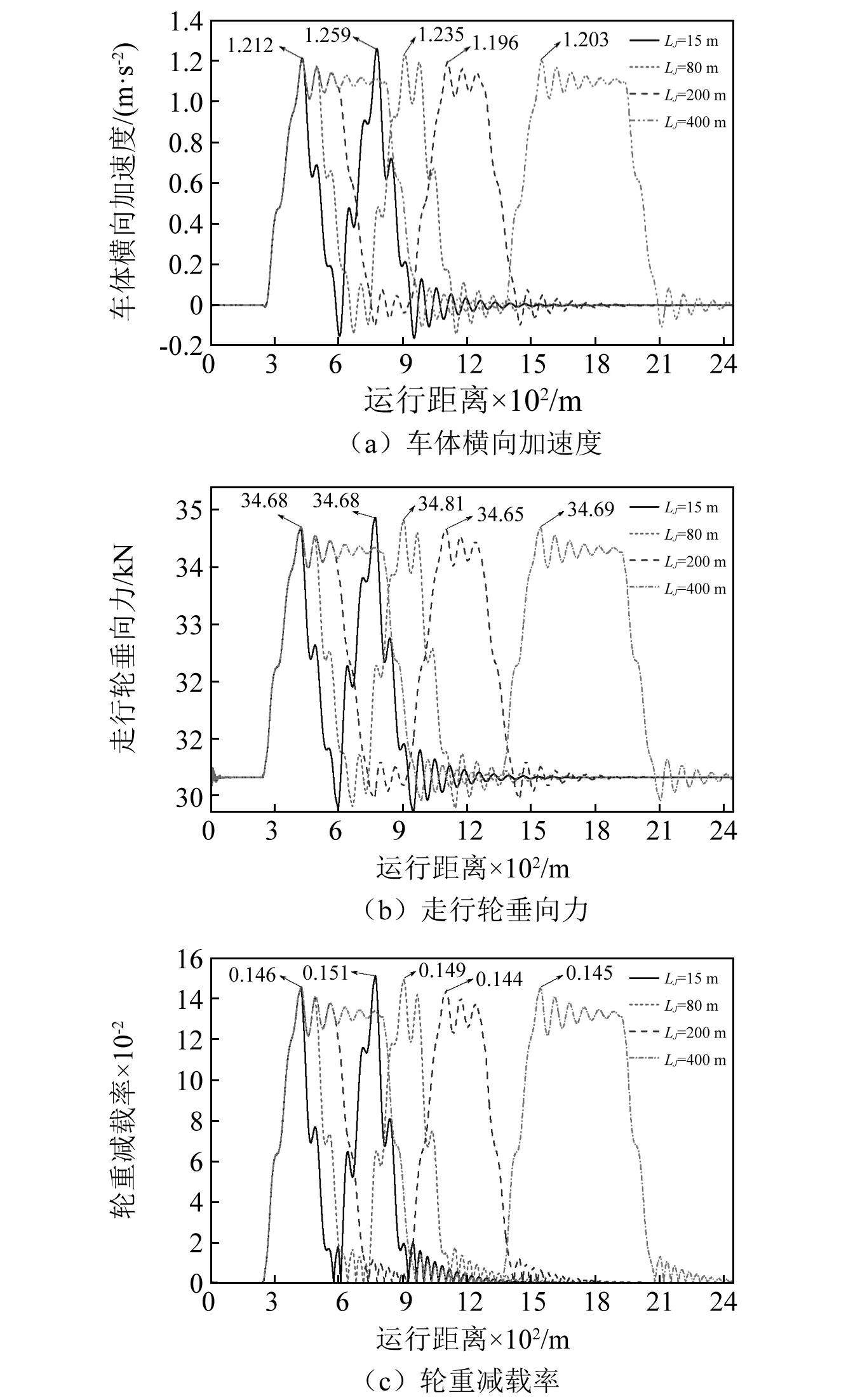
图4 不同夹直线和圆曲线长度下的动力学结果Fig.4 Dynamic results under different length of intermediate straight line and circular curve

将第一、第二段圆曲线设置为反向曲线，可得到同向曲线和反向曲线下的车体横向加速度对比，这里同时考虑了夹直线与圆曲线长度为80 m和400 m两种情况，如图5所示。在反向曲线工况下，当LJ=80 m时，第二段圆曲线处的横向加速度最大值(1.177 m/s2)相比LJ=400 m的结果(1.208 m/s2)减小了2.6%；此时振动叠加会减弱，这与同向曲线工况相反。

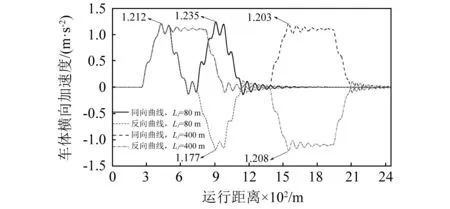
图5 同、反向圆曲线下的车体横向加速度对比Fig.5 Comparison of the lateral acceleration of car body under the same and reverse circular curve

综合来看，当夹直线和圆曲线长度较短(如LJ=15 m，LJ=80 m)时，虽然在夹直线段的振动未彻底衰减完，并产生了振动叠加增强或减弱效应，但尚未对下次的振动有较大影响，振幅与平稳后的结果的差异较小。故在悬挂式单轨线路设计过程中，困难情况下可认为夹直线和圆曲线最小长度不需受到振动叠加的限制。

2.2 不同坡度差下的振动规律

在竖曲线段内，车辆通过变坡点时产生的车体竖向加速度会逐渐衰减，若坡度差(纵断面上相邻两坡段坡度的代数相差值)较小，对应的竖曲线长度就越短，由于振动尚未完全衰减完成，在竖直点产生的垂向振动可能包含前一竖曲线起点处产生的振动，即夹坡段起点处的振动可能是两次振动的叠加[18]。

下面，对不同坡度差下的车体垂向振动规律进行研究，具体工况设置如表3所示，速度为80 km/h，坡度差或竖曲线长度为唯一变量，竖曲线考虑为凹形竖曲线，半径为6 000 m。

不同坡度下车体竖向振动加速度的时程曲线如图6所示。易看到，竖曲线半径相同时，在3‰～60‰的坡度条件下，即竖曲线长度LS=18～360 m时，不同工况下的竖向加速度出现了不同程度的振动叠加现象。当坡度为60‰时，车辆在竖曲线上产生的振动在该竖曲线长度范围内能完全得到衰减。若竖曲线长度不足以满足振动的衰减，竖曲线起点处的振动就会叠加到夹坡段。具体分析如下：

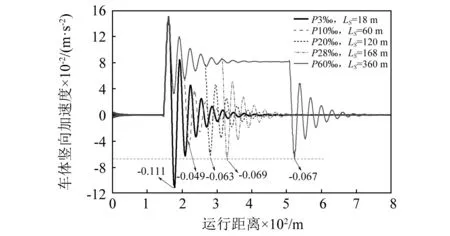
图6 不同坡度差下的车体竖向加速度Fig.6 The vertical acceleration of car body under different slope difference

当坡度为3‰时，竖曲线长度较短，仅为18 m，竖曲线起点处的振动尚未结束，且此时振动方向向下，由于夹坡段起点处的振动方向也是向下，两者振动方向相同，因此振动相互叠加增强，如图中夹坡段处竖向加速度最值的绝对值有明显增大；当坡度为10‰和20‰时，在达到竖曲线终点时的振动方向向上，正好与夹坡段起点处的振动方向相反，因此振动相互叠加减弱；当坡度增大到一定值后，如28‰，即便竖曲线起点处的振动方向向下，此时的叠加增强效应已不是很突出，竖向加速度的最值与60‰坡度条件下的结果(-0.067 m/s2)几乎一致。

图7给出了不同坡度差下的走行轮垂向力结果。随着纵断面坡度的不断增大，走行轮垂向力最大值逐渐增大。当坡度差分别为3‰和10‰时，虽然在夹坡段起点处存在一定振动叠加现象，但效果很微弱，可以忽略不计。因此，走行轮垂向力对坡度差的变化不敏感。

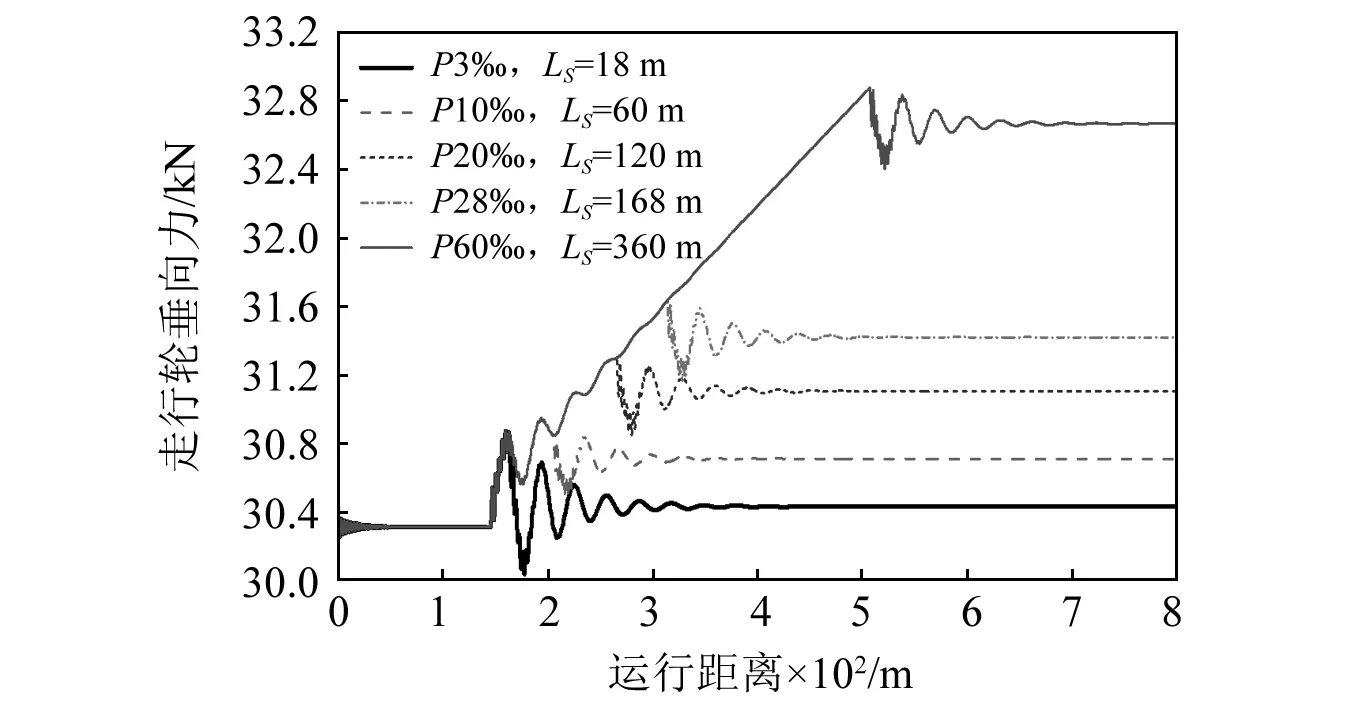
图7 不同坡度差下的走行轮垂向力Fig.7 The vertical force of running wheel under different slope difference

夹坡段起点处的车体竖向加速度最值随坡度差(0‰～60‰)的变化如图8所示。可以看出，线路纵断面坡度在1‰～30‰变化时，车体竖向加速度最值时而增大，时而减小，表明上述所说的振动叠加时而增强、时而减弱(呈谐波衰减波形变化)，这主要取决于竖曲线起点处的振动在到达竖曲线终点后的方向，若与夹坡段起点处的振动方向相同，就会导致振动叠加相互增强，反之则削弱，但振动叠加增强后的竖向加速度的绝对值仍小于竖曲线起点处的竖向加速度最值。由于该型悬挂式单轨车辆的自振频率只有零点几赫兹，相比传统轮轨车辆更低，不同线型短了之后振动叠加效应可能更严重，谐波变化趋势相比传统轮轨系统更明显。另外，坡度差在30‰～60‰变化时，车体竖向加速度最值的变化已不大。

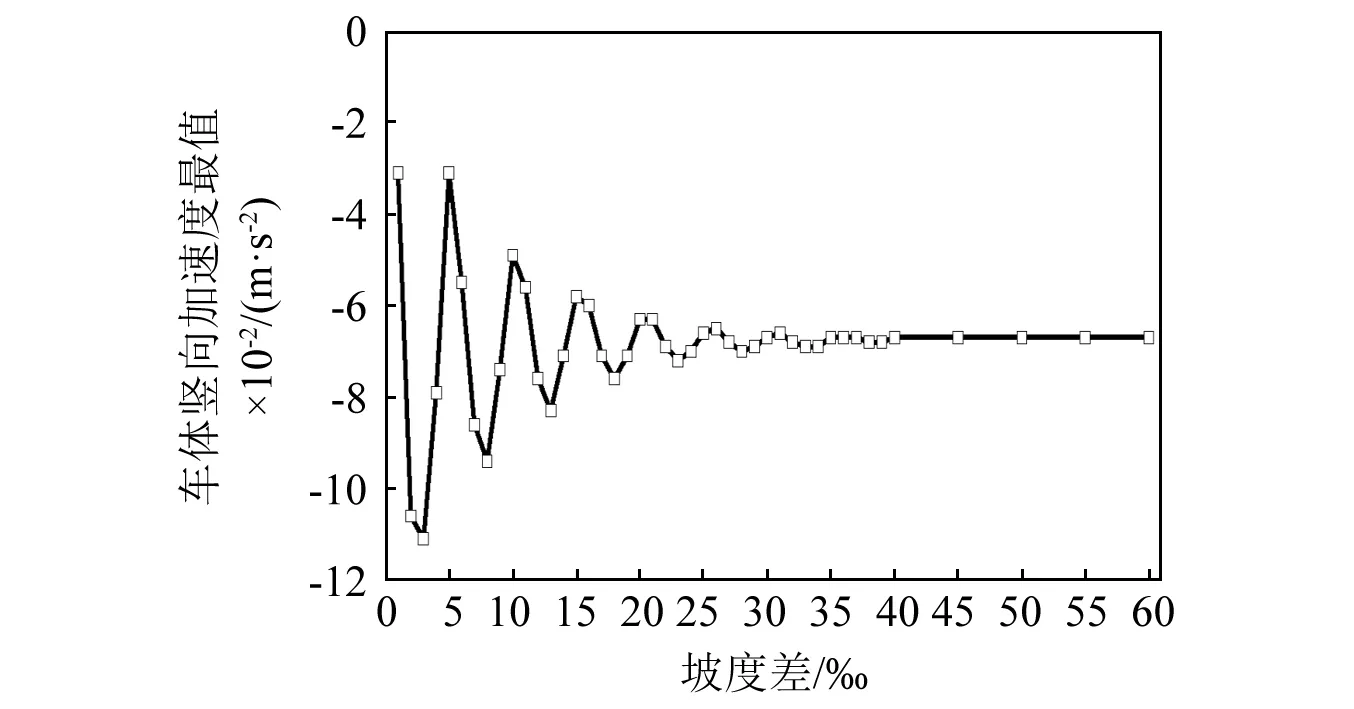
图8 不同坡度差下，夹坡段处的车体竖向加速度最值Fig.8 The maximum vertical acceleration of car body at the intermediate grade sections under different slope difference

2.3 不同夹坡段处的振动规律

改变夹坡段直线长度(纵断面上两相邻竖曲线之间距离在水平面上的投影)进行仿真计算，以分析夹坡段处的振动叠加规律，具体工况设置如表4所示，夹坡段长度为唯一变量，纵断面线型考虑为凹形竖曲线+夹坡段+凸形竖曲线。

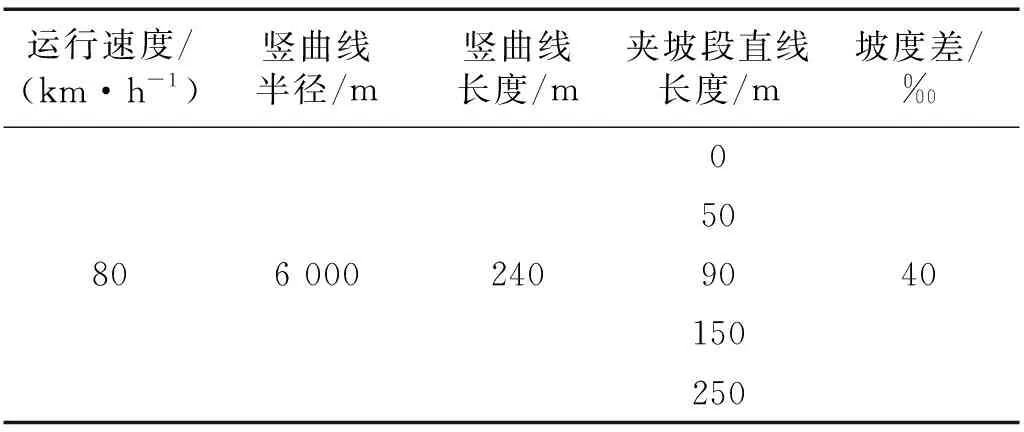
表4 夹坡段长度动力计算线路参数Tab.4 Dynamic calculation line parameter of intermediate grade section length

车体竖向加速度在不同夹坡段长度下的时程曲线如图9所示，竖曲线半径和线路坡度保持不变。可以看到，在夹坡段长度LJ=0～250 m时，不同工况下的竖向加速度出现了不同程度的振动叠加现象，当LJ=250 m时，夹坡段处的振动基本上已完全得到衰减。具体分析如下：

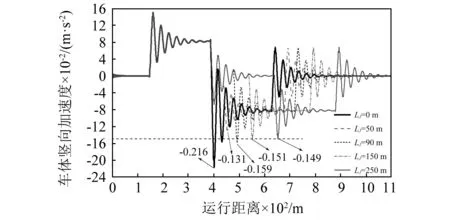
图9 不同夹坡段长度下的车体竖向加速度Fig.9 The vertical acceleration of car body under different length of intermediate grade sections

(1)当LJ=0 m时，即无夹坡段，在第一段竖曲线终点处与第二段竖曲线起点连接处产生了较为明显的振动叠加增强现象。原因是第一段竖曲线终点处振动方向向下，第二段振动方向也是向下，两者振动方向相同，使得振动相互叠加增强。

(2)当LJ=50 m时，第一、第二段竖曲线连接处的振动叠加减弱。原因是车辆在夹坡段运行时会产生振动，夹坡段终点处的振动处于波谷且刚好要向上振动，此时第二段竖曲线起点处也开始振动，方向向下，两者振动方向相反，使得振动相互叠加减弱。

(3)当LJ=90 m时，竖向加速度也会出现振动叠加增强效应，此时第一段竖曲线终点处的振动在夹坡段衰减过程中，刚好达到波峰且将要向上振动，与第二段竖曲线起点处的振动方向相同，使得振动相互叠加增强，但竖向加速度幅值要明显小于LJ=0 m时的结果。

(4)当LJ=150 m时，夹坡段终点正好也是振动叠加增强的位置，但竖向加速度幅值与LJ=250 m的结果几乎相同，表明叠加增强效应不明显，因此，当第一段竖曲线上产生的振动在夹坡段内衰减到一定程度后，竖曲线间的振动叠加效果几乎可以忽略。此时，夹坡段终点处的竖向加速度幅值已约为起点处最大振动幅值的95%，可依据该值确定最小夹坡段直线长度。

不同夹坡段长度下的走行轮垂向力结果如图10所示。当夹坡段长度为0 m时，夹坡段起点处也出现了一定的振动叠加增强现象；当LJ=50 m时，存在振动叠加减弱现象；当LJ=90 m，LJ=150 m时，振动叠加效果不明显，如图10中虚线方框位置。因此，走行轮垂向力对夹坡段长度的变化不敏感。

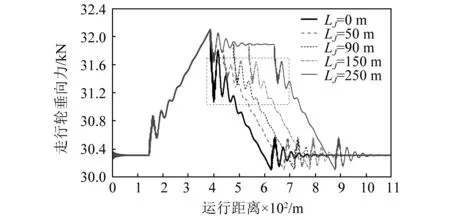
图10 不同夹坡段长度下的走行轮垂向力Fig.10 The vertical force of running wheel under different length of intermediate grade sections

第二段竖曲线起点处的车体竖向加速度最值在不同夹坡段长度下的统计如图11所示，图中也示意了夹坡段范围内该振动曲线的波峰、波谷位置。易看出，夹坡段长度在0～250 m变化时，车体竖向加速度最值存在波动，夹坡段终点与下一段竖曲线起点处的振动方向是否相同是其主要原因，根本原因仍可能是车辆自振频率较低的缘故。由于第二段竖曲线为凸曲线，其起点处的振动开始方向向下，如果夹坡段终点处的振动也朝下，即波峰至波谷这段区域，此时必然产生振动叠加增强现象，若从波谷向波峰运动，则振动叠加减弱，由图9即可看出。当第二段竖曲线考虑为凹曲线时，则波峰至波谷区域的振动叠加会减弱，与凸曲线相反。另外，当夹坡段长度在150～250 m变化时，车体竖向加速度最值的变化已不大。

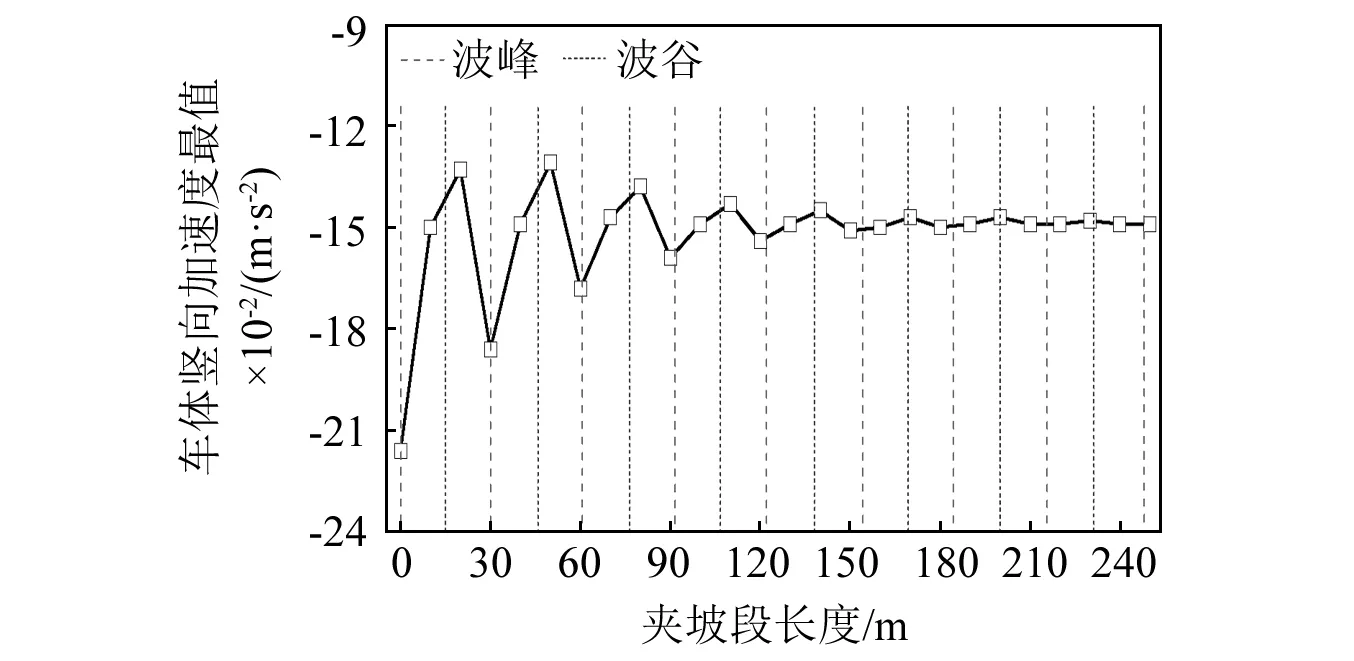
图11 不同夹坡段长度下，夹坡段处的车体竖向加速度最值Fig.11 The maximum vertical acceleration of car body at the intermediate grade sections under different length of intermediate grade sections

根据李向国等的研究可知，传统轮轨车辆通过竖曲线时，在夹坡段处也会存在垂向振动叠加现象，这与本研究中悬挂式单轨车辆在竖曲线处的变化特性相吻合，说明夹坡段长度确实对竖曲线上的垂向动力学指标有一定影响，尤其当夹坡段长度为0 m时的振动叠加作用最强。但对于悬挂式单轨系统来说，还需结合实际线路动力学试验对车辆的运行机理、振动衰减特性做进一步的探索，以更好的支撑线路设计。