压路机激励下重载铁路路桥过渡段动力特性研究
2021-02-26李双龙魏丽敏徐长红
李双龙, 魏丽敏,2, 徐长红, 何 群,2, 周 宏
(1. 中南大学 土木工程学院,长沙 410075; 2. 中南大学 高速铁路建造技术国家工程实验室,长沙 410075)
控制由于路基与桥台之间的刚度差及沉降差引发的线路不平顺问题一直是重载与高速铁路的关键技术,为此必须深入了解路桥过渡段的动力特性。
目前,针对路桥(涵)过渡段动力特性的研究主要集中在“联调联试”或运营阶段,如陈雪华等[1-2]基于秦沈客运专线某路桥过渡段的现场动力测试成果,获得了过渡段动应力、振动加速度等沿线路纵向及深度方向的分布规律;屈畅姿等[3]对武广高速铁路某路涵过渡段分别在“联调联试”和运营阶段进行动力测试,对比分析了过渡段两阶段动力响应的差异;聂如松等[4]开展朔黄铁路某路桥过渡段的现场试验,获得了动应力、动位移与列车轴重的关系;Paixao等[5]结合路桥过渡段现场动力测试,采用数值方法研究了轨道动位移、振动加速度的沿线分布规律。“联调联试”或运营阶段的动力测试反映的是铁路列车荷载激励下轨道-路基结构的综合动力特性。为了进一步掌握路基填筑阶段动力特性,金书滨等[6-7]采用大型振动压路机对填筑阶段的一般路基进行动力测试,研究了动应力在路基不同结构层的传播规律。由于我国梯形过渡段采用填料沿线路纵向逐渐变化的形式实现过渡,在填筑完成尚未铺设道砟及轨枕之前,路基不同横断面动力特性的差异更为突显,研究此时过渡段的动力特性可进一步揭示不同填料层压实状态及其刚度平顺性,而目前有关此方面的研究少有提及。
鉴于此,以蒙华重载铁路某路桥过渡区为试验对象,开展压路机激励下过渡区的动力特性试验,研究路基不同结构层动力响应分布规律,建立考虑振动轮-路基耦合动力数值模型,研究过渡区等效刚度分布及振动轮-路基面接触力变化特性,进一步考察过渡区的刚度平顺性。
1 现场试验方案
1.1 试验工点概况
试验工点位于蒙西至华中重载铁路岳阳—吉安段里程为DK 1578+996.065~DK 1579+018.065路桥过渡区,包含过渡段与一般路基如图1所示。

图1 试验工点现场Fig.1 Test location
蒙华重载铁路是目前国内在建最大规模运煤专线,线路全长约1 814.41 km,设计行车时速120 km/h。试验工点路桥过渡段采用沿线路纵向倒梯形过渡形式如图2所示,沿线长度约为16.0 m,采用A组填料填筑,在线路吉安方向与一般路基填料过渡坡比1∶2。一般路基顶面宽度约8.0 m,基床表层、底层分别厚0.6 m,1.9 m,对基床以下采用C组填料进行换填,厚度约为3.5 m。与过渡段相邻的尚埠大桥采用单线T形桥台。

图2 路桥过渡段结构分布(m)Fig.2 The structure distributionof subgrade-bridge transition section(m)
1.2 监测布置
过渡区共设置三个测试断面,其中一般路基段设置测试断面E,沿深度方向布设5个测点(测点①~⑤);过渡段内设置测试断面T1及T2,沿深度方向分别布设三个测点(测点⑥~⑧)、两个测点(测点⑨,⑩)。各测点主要布设竖向动力响应(振动加速度、振动位移、动应力)测试元件,对距基床表层顶面约0.2 m处的第①、第⑥和第⑨测点,增加埋设纵向、横向水平动应力测试土压力盒,纵向水平土压力盒承压面朝向桥台方向,横向水平土压力盒承压面朝向线路中心线。各测点埋深、所处结构层与填料如图2和图3所示。

图3 监测元件布置Fig.3 Monitoring instrument layout
采用189型压电式加速度拾振器测试竖向加速度,891-2型振动拾振器位移档测试竖向振动位移,并利用INV3060D型采集仪对振动信号进行采集。通过DASP-V10软件对振动信号进行滤波、基线调整等处理,利用全程微积分模块可完成振动信号在时域内的相互转化。动应力响应利用DYB-5型单膜电阻应变式土压力盒进行监测,并通过IMC数采系统进行采集。
1.3 压路机激励动力测试方案
压路机激励动力响应测试在过渡区分层填筑、压实度满足规范要求后进行,路基各结构层压实度指标如表1所示。采用徐工XS202J型压路机,整机工作质量20 000 kg,振动轮宽度2.13 m,直径1.6 m,振动轮分配质量10 000 kg,振动轮与后轮轴距3.18 m。激振强度分为三档:静碾、弱振和强振,各档动力参数如表2所示。行车速度分为三档:Ⅰ档2.54 km/h(0.70 m/s)、Ⅱ档4.97 km/h(1.38 m/s)和Ⅲ档10.51 km/h(2.92 m/s)。由于过渡段长度相对较短且与桥台相连,为确保结构安全,本次试验只使用Ⅰ档和Ⅱ档行车速度。考虑到不同行车方向下过渡段动力响应存在明显差别[8],本次试验设置了两个行车方向(桥台至路基为后退方向、路基至桥台为前进方向,见图2(a)),建立不同动力档数和不同行车速度的测试工况如表2所示,每个工况进行三次重复试验。

表1 路基各结构层压实度指标Tab.1 Compactionfor each layers of subgrade
诸多有关重载铁路的研究成果[9-10]表明,重载铁路路基响应频谱主要集中在0~35 Hz,列车轴重集中在23~30 t。由表2可知,本文采用的压路机周期性振动荷载频率有33 Hz和24 Hz两种,对应的最大激振力分别为245 kN和353 kN(分别相当于轴重为24.5 t和35.3 t的列车荷载)。由此可见,压路机振动荷载水平与重载铁路行车荷载相接近,且激振频率在列车激励频谱范围内。因而,研究压路机激励下路基的动力响应特征一定程度上可为重载铁路路基动力特性的研究提供参考。

表2 试验工况Tab.2 Test schemes
2 试验结果与分析
2.1 路基动应力分布特性
2.1.1 路基动应力时程曲线特征
基于Matlab软件采用五点平滑法对动应力时程曲线进行平滑处理,图4分别给出了路基受压路机激励作用下①号测点竖向及纵向(水平)动应力平滑后的典型时程曲线。由图可知:①在前进方向,测点先后受振动轮及后轮的激励作用,竖向动应力出现两个峰值,而纵向动应力出现4个峰值,原因在于纵向土压力盒能够测得压路机后轮和振动轮分别在土压力盒两侧时的纵向动应力,由于土压力盒的承压面朝向桥台,压路机振动轮及后轮位于土压力盒承压面一侧时的纵向动应力要大于在另一侧时的纵向动应力;②尽管振动轮与后轮分配质量基本相等,但振动轮引起的竖向和纵向动应力约为后轮引起动应力的5倍和2倍左右,表明振动轮的周期激振引起路基的振动水平要比后轮移动荷载引起的振动水平更大。

图4 ①测点典型动应力时程曲线(前进方向)Fig.4 Typical dynamic stress timehistory curve at the measuring point ①(forward direction)
图5给出了E断面不同埋深测点的典型竖向动应力时程曲线。结合图4(a)可以看出,随着埋深增大,竖向动应力逐渐衰减,后轮引起的动应力峰值与振动轮引起的动应力峰值之差逐渐减小,动应力曲线也由“双峰值”逐渐退化为“单峰值”。

图5 不同深度测点典型竖向动应力时程曲线Fig.5 Typical vertical dynamic stress time history curves of different depth points
如图6所示,当压路机以速度v匀速行驶时,对埋深为ΔH的测点,若定义振动轮激励影响时间差为Δt(见图5),则ΔS=Δt·v可理解为振动轮激励下动力波在路基中扩散时的纵向水平影响范围。
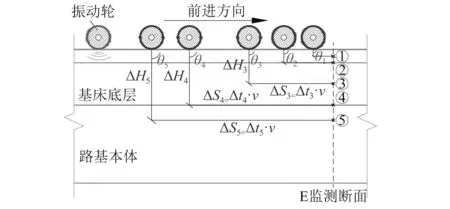
图6 不同深度测点动应力扩散角示意图Fig.6 Schematic diagram of dynamic stress diffusion angle at different depths
实测结果表明:随着振动轮驶向监测断面,埋深最大的⑤测点竖向动应力率先开始增大,然后依次为④,③,②测点,埋深最浅的①测点最后增大。不同埋深测点竖向动应力达到峰值后呈对称性减小,后轮的激励重新引起动应力增大,当超过后轮影响距离后,动应力值趋于0。根据实测动应力时程曲线,可计算振动轮激振下对应于不同深度的动应力扩散角θ=arctan(Δt·v/ΔH)。动应力扩散角能够反映竖向动应力沿路基深度的扩散形态,本次试验获得的振动轮激励过程中路基①~⑤测点动应力扩散角约为78.2°,70.2°,58.3°,58.1°及55.0°。
基于一般路基与倒梯形过渡段在相同埋深测点的动应力数据,可对比分析过渡区沿线动应力扩散角的变化规律。图7为三个测试断面在不同深度测点的动应力扩散角变化情况。
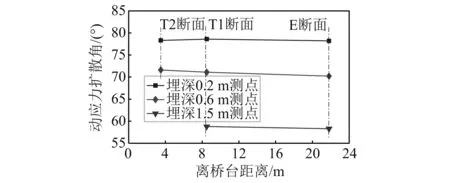
图7 过渡区不同深度测点动力扩散角Fig.7 Diffusion angle of different depth points in the transition zone
从图中可知,三个监测断面中埋深0.2 m测点的扩散角基本保持不变,该位置测点都处于基床表层,填料成分一致,振动轮激振下扩散角变化不大;而在基床底层表面(埋深0.6 m)测点,倒梯形过渡段扩散角略大于一般路基断面,并且全断面填筑A组填料的T2断面要大于T1断面(上层A组、下层C组填料)。一般而言,颗粒级配越好,填料越密实,颗粒咬合程度越高,内摩擦角越大,动应力扩散角也越大,相比一般路基段基床底层的B组填料,倒梯形过渡段采用颗粒级配良好的优质填料,碾压后填料更加密实、整体刚度更大,因而三个断面扩散角存在差异。埋深1.5 m测点扩散角变化规律与埋深0.6 m测点类似。由此可见,压路机激振下路基动应力扩散角与过渡区填料密实度密切相关,基床表层以下相同埋深位置倒梯形过渡段的动应力扩散角要大于一般路基扩散角。
2.1.2 竖向动应力沿深度衰减
压路机激振荷载以动力波的形式在路基传递,由于填料的阻尼作用,动力波沿深度方向逐渐衰减。图8分别给出了不同试验工况下E测试断面不同埋深测点的动应力峰值(三次测试结果的平均值)。

图8 不同埋深测点动应力峰值Fig.8 Dynamic stress peaks at different depths
由图可知,随着埋深的增大,动应力衰减明显,不同工况下①测点动应力在80~125 kPa变化,而埋深2.5 m的④测点动应力仅在5~8 kPa。浅层测点(埋深<2.5 m)受压路机激振条件的影响较大,而深层测点(埋深≥2.5 m)动应力基本不受影响。相同行车速度及行车方向的条件下,浅层测点动应力值随压路机激振强度的增加而增大,例如后退行车方向①号测点强振激振下引起的动应力约为弱振的1.1倍、约为静碾的1.2倍;相同激振强度条件下,浅层测点动应力随压路机行车速度的增大而增大,例如前进行车方向①号测点在弱振Ⅱ档激振下的动应力约为弱振Ⅰ档的1.3倍、强振Ⅱ档激振下的动应力约为强振Ⅰ档的1.5倍。
针对动应力在路基深度方向的衰减特性,韩自力等[11-14]进行了大量研究,得到了表征路基动应力衰减速率的衰减系数。定义衰减系数=基床内某点动应力值/基床顶面动应力。忽略本试验①号(埋深0.2 m)测点元件的填料保护层厚度0.2 m,将①号测点动应力近似作为基床顶面动应力计算不同埋深位置动应力衰减系数。图9给出了本次试验弱振Ⅱ挡工况下的基床动应力衰减系数及其与文献研究结果对比。
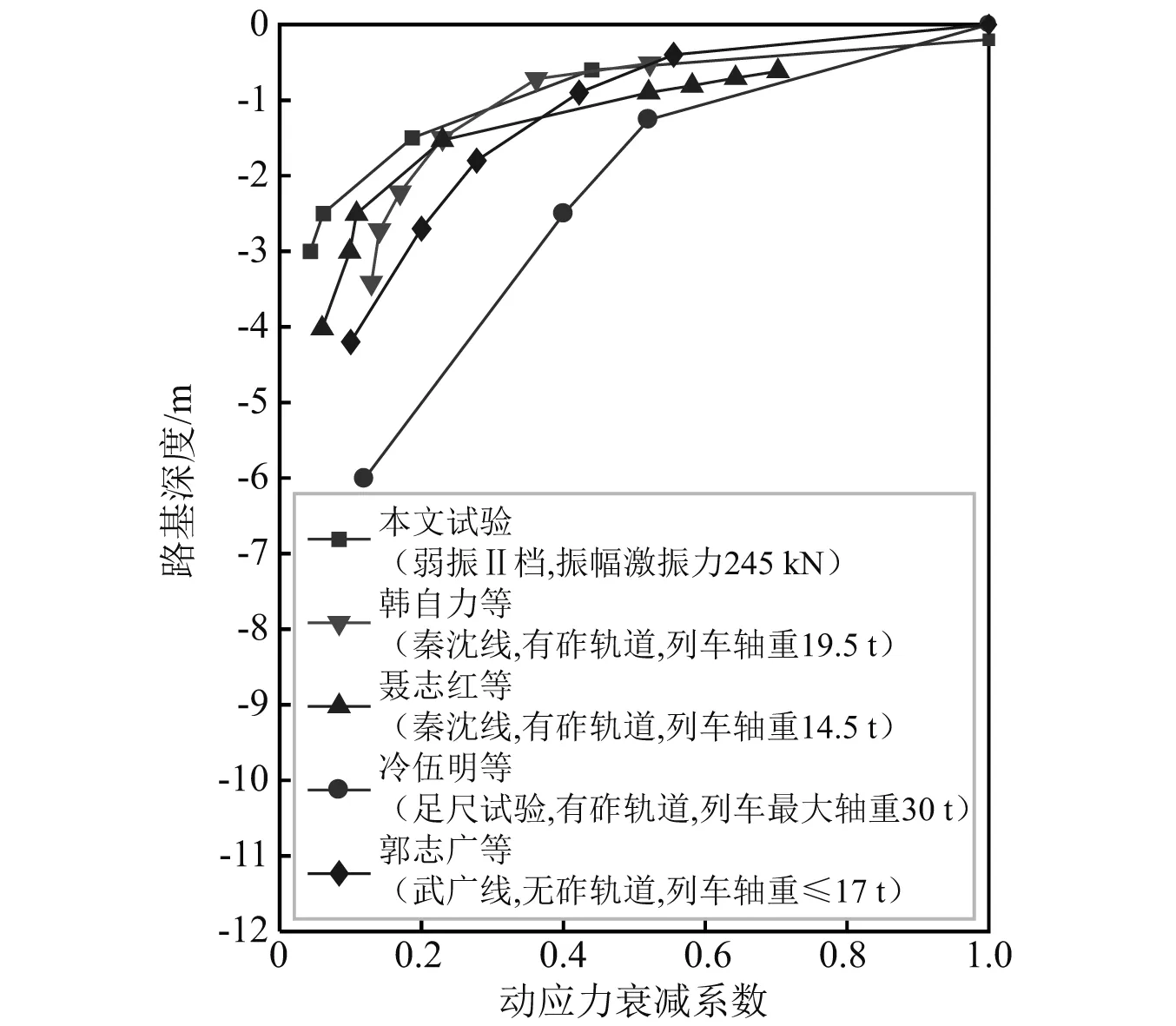
图9 动应力衰减系数与路基深度关系曲线Fig.9 The relationship between dynamic stress attenuation coefficient and subgrade depth
由图可知,因基床表层填料为颗粒级配良好的优质填料,本次试验动应力在基床表层衰减速率最大,基床底层以下动应力衰减速率逐渐减小,与大多实测成果规律基本一致。相比不同轴重下列车行车荷载引起的动应力衰减规律,压路机激励引起的动应力在路基中衰减速率更快,在3.0 m时动应力已衰减至很小。一方面是由于较高的列车行车速度加剧了路基振动水平,导致动应力放大;另一方面,路基受列车轮对激励时刻,邻近轮对动荷载将产生叠加效应。
2.1.3 动侧压力系数探讨
侧压力系数表征土体中某点水平应力与竖向应力之比,可以反映地基土体空间应力状态。目前研究以静止侧压力系数居多,有关动侧压力系数的研究成果少有报道。可根据①,⑥,⑨测点测得的振动钢轮激励下下纵向与竖向动应力峰值之比计算动侧压力系数,探讨路基表层动侧压力系数的影响因素。图10给出了不同试验工况下三个测点的动侧向压力系数。

图10 不同试验工况的动侧向压力系数Fig.10 Dynamic lateral pressure coefficient for different test conditions
图中表明,压路机后退行车条件下测得三个测点动侧压力系数范围0.35~0.53,相应地前进行车条件下为0.24~0.36,后退行车各工况测得的动侧压力系数相比前进行车的整体上要大,主要原因为纵向土压力盒承压面朝向桥台,后退行车时压路机振动轮对土体产生一定的推挤作用,造成纵向土压力相比前进行车时要大,动侧压力系数也要大。从图中还可看出,不同激振工况下,各测点动侧压力系数有一定变化,但变化幅度不大,并且与路基填料存在明显相关性。以后退行车条件为例,一般路基段中的①测点动侧压力系数变化范围为0.49~0.53,而倒梯形过渡段中测点的动侧压力系数变化范围为0.35~0.42,整体上①号测点更大。由于倒梯形过渡段采用A组填料,相比一般路基填料来说,其有效内摩擦角更大,填料更加密实且压缩性更低,相同荷载情况下动侧压力系数相对更小。值得说明的是,由于⑨测点离桥台较近,受桥台动应力波反射作用以及桥台对过渡段填料纵向变形的约束作用,导致动侧压力系数相比⑥测点要大。
2.2 路基振动加速度响应特征
振动加速度是评价外部激励对路基振动冲击及路基振动水平的重要指标。图11给出了不同激振强度下①号测点的加速度时程曲线。

图11 不同工况下①号测点加速度时程曲线Fig.11 Acceleration time history curve of ① measuring point
可以看出,随着压路机激振强度的增大,路基振动水平显著增大。静碾工况下,振动钢轮与后轮激励作用相继引起的振动加速度明显,但幅值较小,振动钢轮引起振动加速度最大值为1.4 m/s2,后轮为0.9 m/s2;而在弱振与强振工况下,后轮引起的振动加速度响应远远小于振动轮激励响应,时程曲线呈现“单峰值”形态,弱振、强振工况加速度最大值比静碾工况都要大,分别为13.2 m/s2,23.5 m/s2。
图12分别给出了弱振I档和强振I档工况下①号测点振动加速频谱分布。由图可知,弱振和强振时路基振动加速度响应基频分别为31 Hz和23 Hz,其他倍频成分逐渐减小。振动响应基频与压路机激振频率十分接近但略有差别,这是因为后轮振动作用会改变振动钢轮作用下路基频谱响应的基频,使得频谱成分略有改变。

图12 ①测点振动加速度频谱分布Fig.12 Vibration acceleration spectrum distribution of ① measuring point
图13为④号测点分别在弱振I档和强振I档工况下的振动加速度频谱分布。从图中可以看出,相比①号测点,弱振I档工况④号测点振动加速度大于100 Hz频段基本已被吸收,而在强振I档工况下,大于150 Hz频段被吸收,表明路基振动频谱高频成分衰减迅速,而低频成分衰减较慢。

图13 ④号测点振动加速度频谱分布Fig.13 Vibration acceleration spectrum distribution of ④ measuring point
3 数值分析
为了更加深入的揭示压路机激励下路桥过渡区的振动特性,采用有限元程序ABAQUS建立考虑振动轮-路基耦合数值模型对过渡区动力响应进行分析。
3.1 模型建立
对包含一般路基、过渡段的过渡区进行精细建模,采用C3D8R单元进行网格划分,如图14所示。数值模型中路基各结构层厚度见图2,过渡区总长32.0 m,一般路基端竖向边界与E断面距离为10.0 m。路基底宽26.1 m,路基以下为复合地基层,厚度6.0 m,复合地基两侧为宽度4.0 m的天然土层。与过渡区相邻的桥台及锥坡采用简化模型,分别在桥台与过渡段、锥坡与过渡段的接触部位设置接触对,桥台与锥坡接触部位采用绑定约束。路基各结构层采用基于摩尔-库伦屈服准则的弹塑性本构模型,地基及其他结构层均采用线弹性本构模型,计算参数如表3所示。
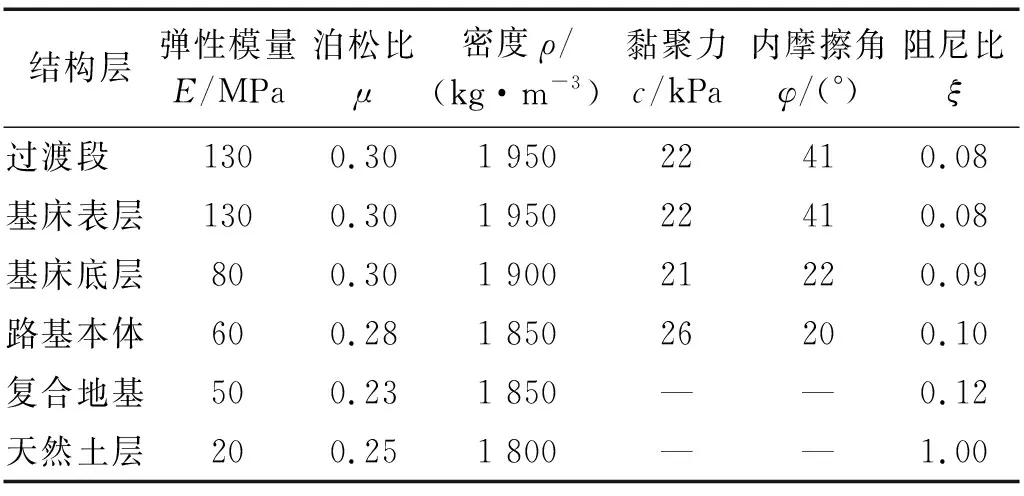
表3 主要结构层计算参数Tab.3 Main structural layer calculation parameters

图14 数值网格Fig.14 The grid of numerical model
简化压路机车辆结构,仅考虑振动钢轮对路基的激励作用。将振动钢轮简化为刚体,采用面-面接触描述振动钢轮与路基顶面的相互作用,设置钢轮圆柱面为主面,路基顶面为从面,接触面法向作用采用“硬接触”,切向作用采用“罚”函数,摩擦因数取0.2。根据Mooney等[15-16]的研究成果,压路机振动钢轮的激振力可用以式(1)描述
Fs(t)=Fevcos(ωt)+mdg-mdad
(1)
式中:Fs(t)为某时刻振动钢轮对路基面的激振作用力;t为时间;Fev为偏心块振幅离心力;ω为振动圆频率;mdg振动钢轮分配重力,本文约为100 kN;mdad为振动轮惯性力,考虑到压路机车辆内部结构的阻尼作用,本文予以忽略。根据压路机不同激振强度参数(见表2)确定振动钢轮弱振及强振工况的数值模型激振作用力Fs(t)。由于在计算分析的初始步中已对振动钢轮施加了重力荷载100 kN,因而在模型内仅输入离心激振力模拟弱振和强振工况,输入的部分时程曲线如图15所示。
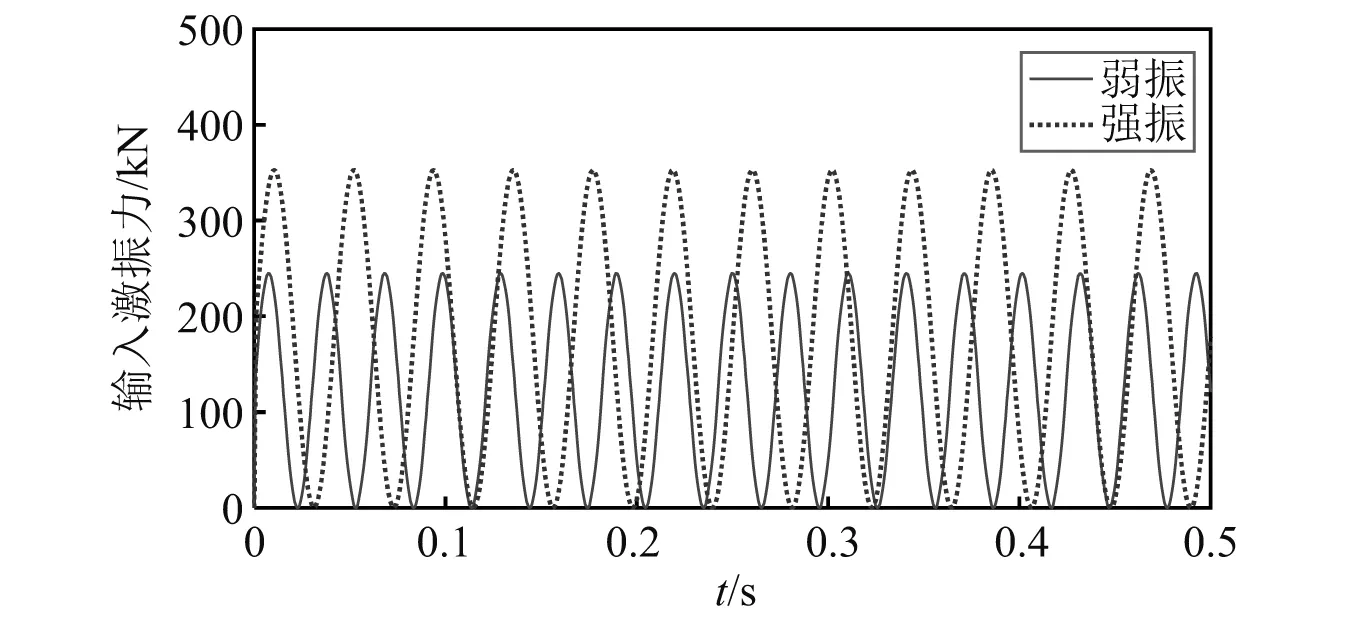
图15 数值模型输入离心激振力Fig.15 The centrifugal excitation force in numerical model
模型底部边界采用位移固定约束,模型横向及纵向边界采用法向位移约束。在一般路基端竖向边界与纵向边界(天然土层)设置黏弹性人工边界单元以防止应力波在边界处的反射,设置阻尼比为1.0。计算过程:①计算初始地应力场(初始位移场清零);②对振动钢轮施加重力荷载计算初始静力平衡状态;③以②计算应力场为初始状态,同时赋予钢轮滚动速度边界条件,模拟静碾工况;④以②计算应力场为初始状态,同时施加激振力荷载,并赋予钢轮滚动速度边界条件,模拟弱振和强振工况。
3.2 模型验证
为了验证模型的可靠性,以前进行车方向在弱振Ⅱ档工况条件下为例,将数值分析结果与试验数据进行对比。图16(a)为单周期激振力最大时刻路基纵剖面动应力云图。
由图可知,振动钢轮激励作用下,路基层应力等值线呈“灯泡”分布,钢轮与路基接触部位动应力最大,动应力向路基深处扩散。提取①~⑤测点单元动应力值分别为114.09 kPa,66.13 kPa,29.45 kPa,4.42 kPa及2.10 kPa,比实测值分别大4.07 kPa,-6.48 kPa,10.99 kPa,-2.10 kPa及-2.31 kPa。可见,数值结果与试验结果相差不大。图16(b)给出了①号测点单元动应力时程曲线对比,计算动应力响应频率与激振频率基本一致,动应力分布规律和峰值与平滑后的实测动应力曲线都较为一致。

图16 动应力对比Fig.16 Comparison of dynamic stress between numerical results and measured data
图17给出了①号测点振动加速度时程曲线对比。图中表明,振动轮越接近测点,振动加速度越大,且振动频率与激振频率一致。数值分析所得最大值为15.92 m/s2,相应的实测值为11.67 m/s2,两者在分布规律上基本吻合。综合动应力与加速度对比情况可知,数值分析结果与实测数据的分布规律与量值较为一致,说明计算模型与参数合理。

图17 振动加速度对比Fig.17 Comparison of vibration acceleration between numerical results and measured data
3.3 计算结果分析与讨论
3.3.1 路基沿线路等效刚度分布
轨下刚度突变会引发线路不平顺问题,严重时致使列车产生跳车现象[17]。路桥过渡段轨下刚度的平顺过渡对轨道结构的服役寿命及列车安全运营至关重要。根据Esveld[18]提出的计算方法,竖向轨下刚度可由式(2)获得
K=Q/z
(2)
式中:K为竖向轨下刚度;Q为列车荷载;z为列车移动荷载引起轨道竖向动位移峰值。本次试验工况包含了振动钢轮无偏心激振的静碾工况,获得了沿线路纵向三个测点的路基顶面竖向位移(忽略①,⑥,⑨测点元件0.2 m的覆盖填料保护层厚度,将①,⑥,⑨测点竖向位移作为路基顶面位移),根据振动轮分配重力荷载(Q=100 kN)可计算三个断面等效刚度。
图18给出了路基顶面动位移及路基沿线等效刚度分布的数值结果与实测结果。从图中可以看出,两者较为接近,但实测值对应的埋深为0.2 m,比路基顶面位移更小,故所得等效刚度比数值分析结果稍大。

图18 过渡段沿线等效刚度分布Fig.18 Equivalent stiffness distribution along the transition section
数值结果表明,在距台背5~16 m,路基等效刚度呈线性减小趋势,从结构上看,该区段处于倒梯形过渡段的渐变过渡部位。最大等效刚度出现在全断面为A组填料的过渡段断面,为87.2 kN/mm;最小刚度出现在一般路基断面,为74.8 kN/mm。我国有砟轨道整体刚度为90~130 kN/mm[19],本文数值分析结果与之较接近,但因没有考虑钢轨、轨枕及道砟等,刚度计算值偏小,加之试验时期为梅雨季节,所得等效刚度实测值也有所偏小。
3.3.2 振动轮-路基面接触力变化特性
图19给出了台尾至E断面(长22.0 m)路基在静碾Ⅱ档及弱振Ⅱ档工况下的振动轮-路基面接触力变化曲线,强振工况与弱振工况规律类似,不再赘述。
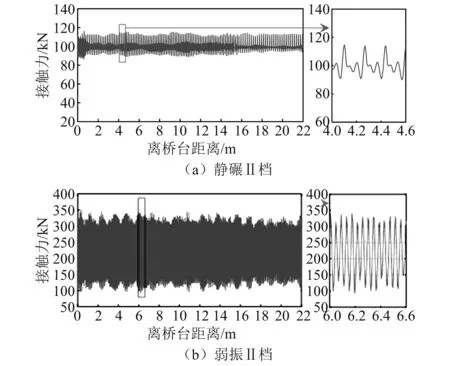
图19 不同激振强度工况接触力对比Fig.19 Comparison of contact force under different excitation strength conditions
由图可知,静碾与弱振激振引起的接触力变化形态有显著差别。静碾工况条件下,路基面只受振动钢轮重力移动荷载,接触力变化围绕100 kN之间波动,波动范围为90~115 kN;而在弱振工况下,路基受振动轮偏心激振力及重力作用,接触力变化与式(1)模型所施加的激振力Fs(t)曲线较为一致,大约在100~350 kN循环变化,循环周期与输入激励周期一致。值得注意的是,两种激振工况下,在倒梯形过渡段内振动轮-路基面接触力峰值都比一般路基段大,在距台尾大约16.0 m开始,接触力峰值开始增大,至离桥台大约5.0 m时,峰值趋于稳定。静碾工况下接触力最大峰值相比一般路基断面增大了约1.7%,弱振工况增大了约3.3%,可见激振强度越强,波动峰值增大现象越明显。
为了进一步研究倒梯形过渡段与一般路基刚度差对接触力的影响,以弱振工况为例,通过提高过渡段弹性模量来表征刚度差的变化。保持一般路基材料参数不变,倒梯形过渡段A组填料弹性模量分别设置为150 MPa,180 MPa,210 MPa和240 MPa,计算过渡段振动轮-路基面最大接触力峰值相比一般路基断面的增幅。图20给出了不同弹性模量对应的最大接触力峰值增幅变化。

图20 不同弹性模量下的最大接触力增幅Fig.20 Maximum contact force increase in transition section under different elastic moduli
由图可知,随着过渡段弹性模量的增大(过渡区刚度差的增大),最大接触力峰值增幅呈增大趋势,当倒梯形过渡段弹性模量达240 MPa时,增幅约为4.2%,由此表明过渡区刚度差越大,接触力放大现象越明显。这也正是列车在路桥过渡区容易引发行车不平稳的诱导因素:车速足够大时,刚度差导致接触力的急剧变化会引起车辆在经历路桥过渡段时的垂向加速度突然变化,进而引发颠簸、跳车等现象。
4 结 论
采用现场试验结合数值分析方法,研究了压路机激励下路桥过渡区动力响应时空分布规律,分析了路基、过渡段等效刚度的分布及振动轮-路基面接触力的变化特性,得出以下结论:
(1) 压路机激励下,随着测点埋深的增大,动应力时程曲线由“双峰值”逐渐退化为“单峰值”分布,同时动应力扩散角逐渐减小;相同埋深处,倒梯形过渡段的动应力扩散角大于一般路基段。
(2) 浅层测点(埋深<2.5 m)动应力随激振强度、行车速度的增大而增大;随着埋深的增大,动应力衰减幅度逐渐减小,基床表层衰减率最大。相比列车荷载,压路机激励引起的动应力在路基中衰减速率更快。
(3) 由于纵向土压力盒承压面朝向桥台,受压路机振动轮在路基浅层的推挤作用,驶离桥台方向时的基床表层动侧压力系数要大于驶向桥台方向,前者为0.35~0.53,后者为0.24~0.36。动侧压力系数与压路机激振强度、行车速度无明显相关性,而与路基填料有关,倒梯形过渡段的动侧压力系数值要小于一般路基段。
(4) 路基振动加速度随压路机激振强度的增大而增大,后轮振动会引起振动轮作用下路基振动响应基频的小幅降低。随着路基深度增大,振动加速度频谱高频成分先于低频成分被吸收。
(5) 试验与数值分析结果表明,过渡段整体刚度在74.8~87.2 kN/mm,随离桥台距离增大而呈线性减小趋势,过渡区刚度平顺性良好。振动轮激励过程中,过渡段的振动轮-路基面最大接触力峰值比一般路基段要大,一般路基与过渡段刚度差越大,过渡段最大接触力峰值也越大。
