基于Triangle Net 的密集人群计数

翁佳鑫,仝明磊

(上海电力大学 电子与信息工程学院,上海 200090)

1 概述

近年来,人群计数的典型解决方案是使用基于卷积神经网络(CNN)的密度回归估计人群密度,通过训练CNN 来学习人群图像和密度图之间的映射,再通过密度图求和获得总人数。MCNN[1]是将多尺度融合应用于人群计数的开拓性工作,使用三个不同大小的卷积核模块解决人场场景中规模变化问题。Switch-CNN[2]在图像块上训练几个独立的CNN 人群密度回归器,这些回归器与MCNN 具有相同的结构。此外,还对回归分类器进行了交替分类训练,以选择最佳分类器进行密度估计。虽然以上两个网络使用多列模块但几乎使用相同的结构,不可避免地导致大量信息冗余；且在将图像发送到网络之前,多列网络始终需要密度分类器,使网络结构变的更复杂。Maesden 等人[3]提出了一种用于单图像人群计数的多尺度卷积神经网络(MSCNN),通过膨胀卷积和Inception 结构在单列架构中实现更高的人群计数性能。SaCNN[4]是一种具有规模自适应的CNN,它以具有固定小接受域的FCN 为骨架,并将从多层提取的特征图改变为相同大小,然后将它们融合以生成最终密度图。由于高分辨率密度图包含更精细的细节,所以生成高分辨率和高质量的密度图对人群密度估计很有帮助。ic-CNN[5]提出了一个两分支网络,其中一个生成低分辨率密度图,另一个将低分辨率图和前一层提取的特征图融合以生成更高分辨率的密度图。但该模型生成低分辨率密度图时欠缺考虑浅层网络的细节信息,人群较为密集时难以提取到小尺度人头的特征。

针对上述问题,本文提出的模型首先用并行连接的方式将浅层网络提取的细节信息和深层网络提取的高分辨率表征进行多尺度融合生成高质量密度图；其次提出加固模块以考虑密度图的局部相关性且加快模型收敛速度；最后提出一种新的损失函数,在人群计数常用的均方误差(MSE)损失函数的基础上联合二进制交叉熵(BCE)损失。

2 人群密度估计

为解决人群计数算法在拥挤环境下精度下降的问题,提出了新颖的编码器/解码器网络Triangle Net。

图1 Triangle Net 网络结构

2.1 网络结构

如图1 所示,本文提出的网络以编码解码器结构为基础。网络中每个卷积核大小为 3×3,每个最大值池化核的大小为 2×2。

编码器模块使用VGG16 的前10 层作为网络的特征提取器,在特征提取的过程中增加池化层对图像进行下采样操作,能够有效地降低网络参数量,扩大感受野,同时生成4 种不同分辨率的特征图。

解码器分为密度图估计模块和加固模块。现有的大多数方法通过最大池化生成低分辨率特征图,再从低分辨率特征图通过上采样恢复至高分辨率,实现了多尺度特征提取的一个过程。这种方法并没有考虑到浅层网络的细节信息,当人群较为密集时,很容易提取不到小尺度人头的特征。不同尺度的特征图包含不同信息并且高度互补。例如,较深层特征可以提取出高级语义信息,而在浅层特征中可以获得更多细节信息。有一些这方面的研究[6-7]表明,这些互补特征可以相互完善。但若使用简单方法如加权平均和串联来直接融合,则不能很好地捕获这些互补信息,所以本文使用并行连接深层网络和浅层网络的方式,多尺度融合不同分辨率的特征图,使得从深层网络到浅层网络的过程中都从其他并行表示中反复接收高阶语义信息,有效解决像素定位问题,提高生成密度图的质量。

加固模块通过上采样恢复特征图尺寸,每经过一次上采样恢复的特征图就与密度图估计模块的特征图融合,这样既能影响密度图估计模块,还能帮助网络更快的收敛。最后融合密度图估计模块和加固模块,通过ReLU激活函数将其送到最后的conv1×1×1 层,生成高精度人群密度图。

2.2 损失函数

本节使用由均方误差(MSE)和二进制交叉熵(BCE)损失组成的联合损失。现有人群计数算法大多使用SSIM损失来确保不忽略密度图的局部相关性,但是在本文实验中,发现加固模块不仅能加速收敛并且可以用来影响密度图估计模块。这样,不仅可以帮助网络更快地收敛,还可以帮助检查密度图的局部相关性。

MSE 损失：Hang 等人[8]在他们的图像恢复研究中,发现了一个有趣的现象,在独立且均匀分布的高斯噪声的情况下,L2 提供了最大似然估计。通常使用基于像素独立性假设的欧几里得距离,会忽略掉密度图的局部相关性。但由于本文中的加固模块能有效的解决这个问题,所以选择使用MSE 损失函数,如式(1)所示

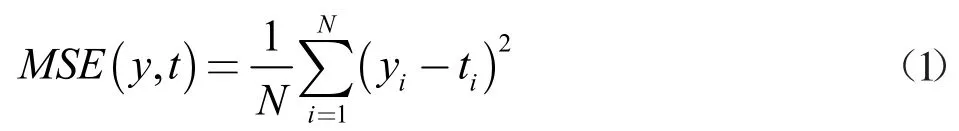
其中y 是预测值,t 是真实值,N 是像素总数。

BCE 损失：本文选用分类交叉熵损失函数来训练加固模块。

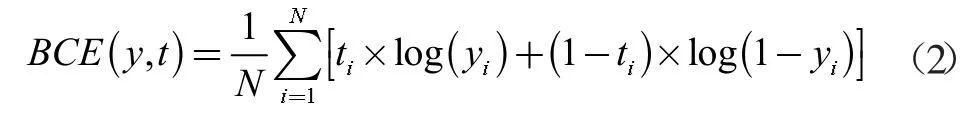
其中y 是预测值,t 是真实值,N 是像素总数。

2.3 评价指标

本文选用回归问题常用的平均绝对误差(MAE)和均方误差(MSE)作为评价指标,MAE 可以反应算法的准确性,而MSE 则反应算法的鲁棒性,定义如(3)(4)两式所示。

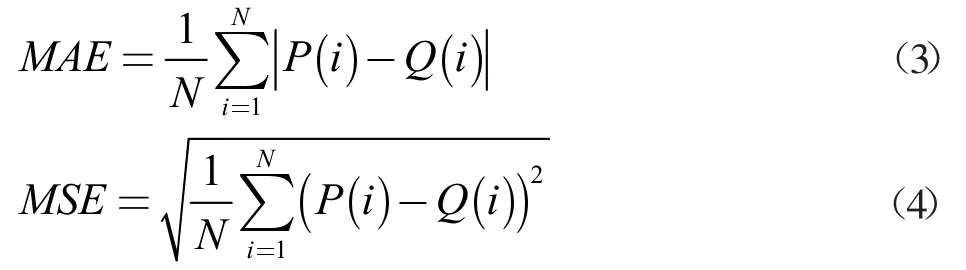
其中N 为测试集图片的总数量,P(i)为测试集标记的真实人数,Q(i)为测试集的预测人数。

3 实验

本文将在两个较为密集的人群计数数据集上进行,这两个数据集是ShanghaiTech 和UCF_CC_50。

3.1 训练细节

深度度学习网络框架为Tensorflow+ Keras,模型训练参数如表3 所示。在训练网络时,出现了梯度逐渐消失的问题,尝试使用批理规范化(BN)和实例规范化(IN)来缓解此问题,但由于小批量统计信息不稳定,使用BN 时会得到更差的结果。因此选择在每个卷积层后加入IN层,如式(5)所示

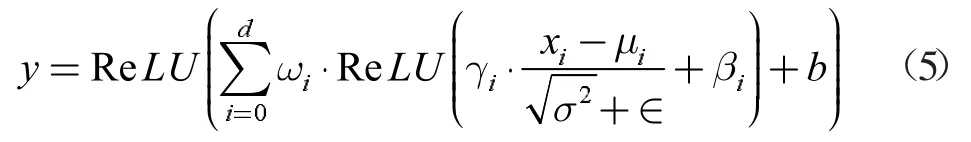
其中w 和b 是卷积层的权重和偏差项,γ 和β 是实例规范化层的权重和偏差项,μ 和σ 是输入的均值和方差。

3.2 数据集

实验在ShanghaiTech 和UCF_CC_50 两个通用人群密度估计数据集上进行,这两个数据集的参数如表1 所示。本文只使用一种数据增强方式是水平翻转。

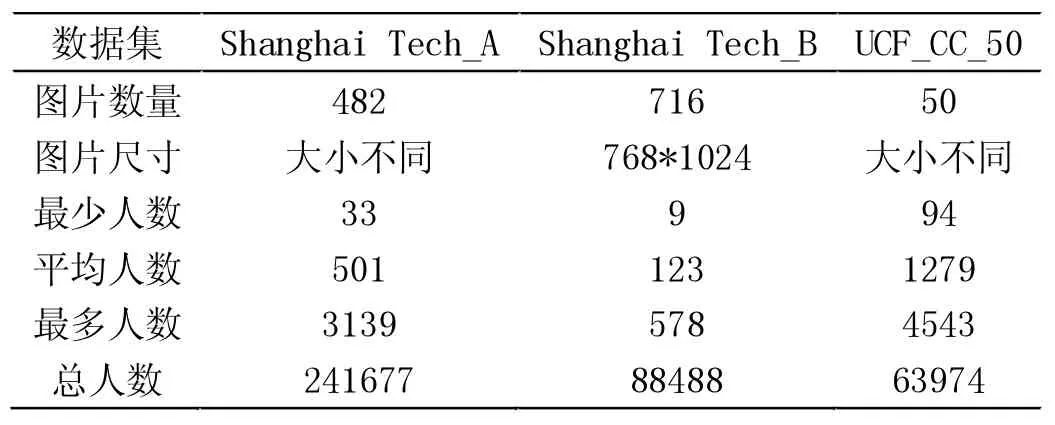
表1 数据集参数

3.3 Shanghai Tech 数据集

Shanghai Tech 数据集是最大的人群密度公共数据集,可分为A,B 两部分,A 部分的人群密度远大于B 部分。其特点是场景变化多,且人群密度变化也大,具有较高的复杂性和挑战性。

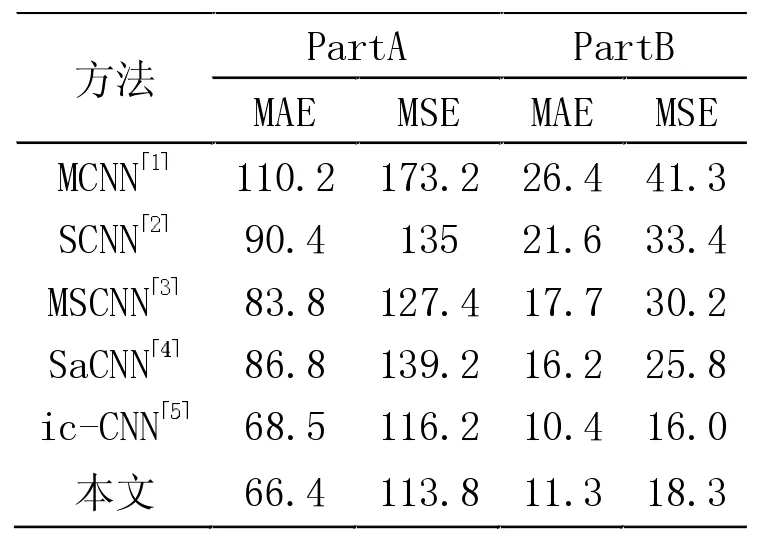
表2 不同实验在Shanghai Tech 数据集上的对比

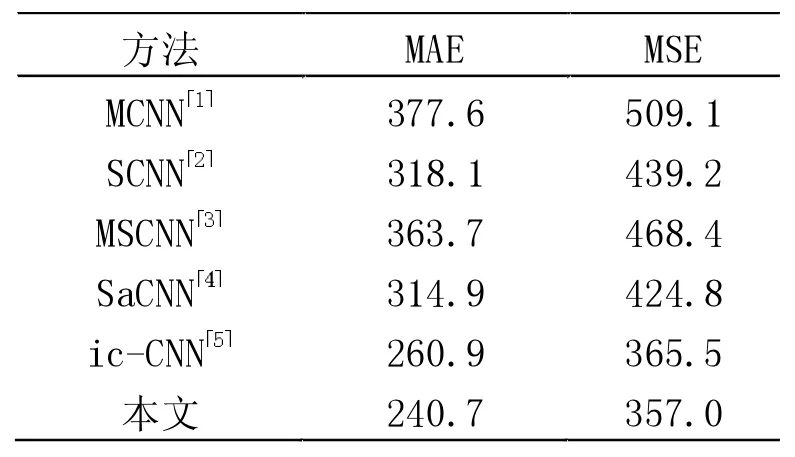
表3 不同实验在UCF_CC_50 数据集上的对比

表2 将本文提出的算法与其他人群计数算法在Shanghai Tech 数据集进行了比较,从表中可知本文在PartA 部分取得最小的MAE 和MSE,而在PartB 部分的MAE 和MSE 仅比ic-CNN 大一些。从实验结果表明,本文提出的算法在较为稀疏的人群上能取得不错的效果,并且在较为密集的人群上取得的效果更加。

3.4 UCF_CC_50 数据集

UCF_CC_50 数据集总共50 张图片,这个数据集虽然图片数量最少,但人群最为密集,且每张图片的人数变化大,是最有挑战性的数据集。本文选择与文献[1]一样的五折交叉方法进行实验,各个不同算法在UCF_CC_50 数据集上的结果如表3 所示。本文提出的算法在MAE 和MSE 上均取得最小值,充分证明本文提出的算法在较为密集的人群上能取得不错的准确性和鲁棒性。

4 结束语

为了提高人群密度算法在拥挤人群的精度,本文提出了一种新颖的编码解码器网络Triangle Net,用并行连接深层网络和浅层网络的方式,多尺度融合不同分辨率的特征图,使得从深层网络到浅层网络的过程中都从其他并行表示中反复接收高阶语义信息,提高生成密度图的质量,并且加入的加固模块既能加快网络收敛,还能有效解决密度图的局部相关性问题。在两个具有拥挤嘈杂特征的数据集上进行大量实验表明,本文的方法在较为密集场景下人群计数有着不错的准确性和鲁棒性。

本文进行实验的两个数据集都较小,未来考虑自主生成不同密度的虚拟人群图像作为训练集来扩充数据集以提升人群计数的准确度。