无限大多层层合板隔声量分析

王鹏伟，孙维光，董仕杰，陈 杰，张立民

（1.西南交通大学 牵引动力国家重点实验室，成都610031;2.青岛四方机车车辆有限公司，山东 青岛266111）

多层层合板指由两层以上的单层板以紧密结合的方式成为整体的结构单元体，可以由不同材质的单层板所组成[1]。一般用于分析由多层介质组成的复杂结构的理论方法有波传递法、传递矩阵法和阻抗分析法等。Mu等[2]利用波传递法计算了多层穿孔结构的声能透射损耗；黄梦情等[3]将结构弯曲波引入到波传递法，分析了带空腔的双层板结构；万翾等[4]在无限大板假设前提下，分析了由各向正交异性材料所构成的多层层合板的传声损失；Feng[5]利用传递矩阵法和试验结果比较，将多层结构的声学特性与各层的反射和透射系数联系起来；Liu[6]采用传递矩阵法，将多孔弹性材料双层结构的理论模型推广到三层结构中；Fringuellino 等[7]在不考虑声波在传播过程中损耗的前提下，用阻抗分析法分析了三层层合板的隔声；王佐民等[8]应用阻抗分析法探讨了具有确定平面尺寸和边界条件的双层板结构的隔声量。

以上研究大多数局限在由三层不同介质组成的结构，对于三层以上的结构则研究较少。本文将在单层薄板隔声量计算理论的基础上，通过引入经典层合板弯曲刚度计算公式，提出“等效薄板法”，将单层薄板计算公式推广到多层层合板结构，可用来分析任意多层且总厚度较薄的多层层合板结构的隔声性能。

1 单层薄板隔声量计算

1.1 整体振动的单层均匀柔性薄板隔声量计算

柔性薄板是指厚度很小以至于前后表面介质的法向速度相同的薄板，如图1所示，其中pi代表入射波，pt代表透射波。

图1 整体振动的单层薄板声透射示意图

声阻抗率是声场中某位置的声压与该位置的质点速度之比。设声波入射角为θ，薄板的声阻抗率为Zsm，薄板两侧介质特性阻抗为ρc，其中ρ 和c 分别为介质的密度和声速，介质的声阻抗率则为Zs=ρc/cosθ，此时在入射界面处的声压反射因数为[9]

设薄板质点法向振动速度为vm，两侧声压分别为pf和pb，两侧介质质点法向振动速度分别为vf和vb，则有：

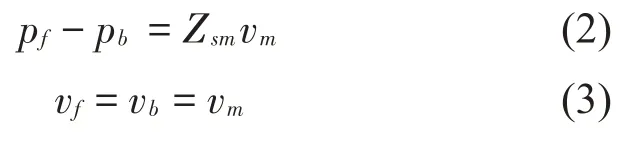
根据声阻抗率的定义，引入等效局部法向声阻抗率的概念：等效局部法向声阻抗率是声场中某点的声压与质点法向速度的比值，在声场中多层介质的界面连续并与入射角有关。设Zf和Zb分别为薄板前后表面的等效局部法向声阻抗率，在薄板前表面即声波入射端处，因为同时存在入射波和反射波，故Zf不等于入射波的法向声阻抗率；而在薄板后面因为仅有透射波，所以Zb=Zs。结合式（2）与式（3），得：

继而可得：

结合式（1）可得在入射界处的等效声压反射因数为

将式（4）和式（6）代入式（5），并利用Zb=Zs，得：

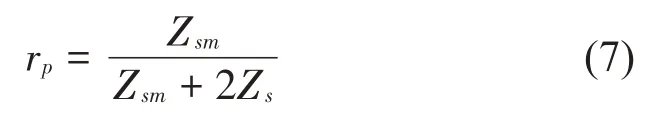
利用式(7)得到薄板前界面介质中质点速度为

薄板以及前后分界面介质中质点速度为

由式（8）和式（9）得声压透射因数为

板的隔声量计算公式为

将式（10）代入式（11），得：

根据牛顿第二定律可知：

式(14)中：m为薄板面密度。将v=vaejωt代入上式，并联合式（2）可得薄板的声阻抗率为

将式（15）代入式（13）得：

1.2 弯曲振动的单层均匀薄板的隔声量计算

在声波斜入射到薄板结构的情况下，除了产生纵波之外，还会产生使薄板进行弯曲振动的横波，也叫弯曲波。如图2所示。弯曲波是剪切波和纵波的组合，对于各向同性板，在角频率为ω 的声波激励下，弯曲波的传播速度cB为[10]

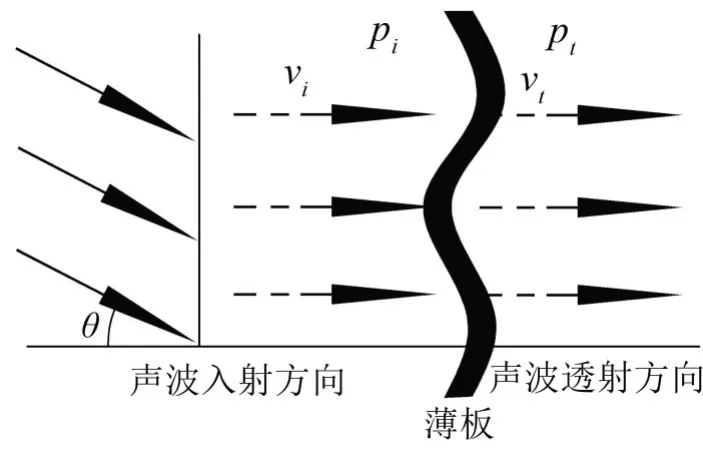
图2 弯曲振动的单层薄板声透射示意图

式(17)中：B为弯曲刚度，由下式给出：

其中：m为薄板面密度，h为厚度，E为杨氏模量、σ为泊松比。

由式（17）可知，弯曲波的传播速度随着声波频率的增加而增加，因此必然会存在一个临界频率fc，使得弯曲波传播速度等于声波在介质中的传播速度。临界频率也叫吻合频率，单位为Hz，由下式给出：

弯曲振动的单层均匀薄板声阻抗率Zsm与cB有关，可写成[9]：

联立式（17）、式（19）和式（20），并考虑到弯曲振动存在能量损耗，得到无限大且包含损耗的单板的声阻抗率为

式(21)中：f为声波频率，单位为Hz，η为板的能量损耗因子，与材料和单板的边界条件有关，一般取值范围在0.01～0.001 之间。将式（21）代入式（13）即可求得在入射角为θ时隔声量。考虑实际情况下声波入射角度为0°～78°，因此通过对入射角加权平均得混响声场中单板隔声量为：

2 等效薄板法

根据上述分析可知，弯曲刚度是计算薄板隔声量的关键因素。当层合板的弹性特性与单层薄板相近且面积足够大以致于可以忽略板的边界效应时，可将层合板等效为一个单层均匀薄板，通过引入由经典层合板理论所得出的弯曲刚度计算公式，继而计算出层合板的隔声量。

建立经典层合板理论有四点假设前提[1]：

（1）层合板各单层板之间粘结牢固且有共同的变形，不产生滑移；

（2）各层单板可近似认为处于平面应力状态；

（3）层合板变形前垂直于中面的直线段在变形后仍为垂直于中面的直线段，且长度不变；

（4）平行于中面的各截面上正应力可以忽略不计。

在以上假设前提下，设（x，y）面在层合板中线处，如图3所示，则层合板的弯曲刚度计算公式为

图3 多层层合板弯曲刚度示意图

式(23)中：Ek为第k层板的杨氏模量，σk为第k层板的泊松比，lk为第k层板的厚度，zk为第k层板中线到（x，y）面的坐标。

联立式（12）、式（19）、式（21）、式（22）和式（23）即可求得扩散声场中多层层合板的隔声量：

3 多层层合板隔声量对比

分别对由不同材料组成的三层、四层和五层层合板隔声量做计算，并与统计能量法（SEA）计算结果进行比较，论证等效薄板法的可行性。统计能量法是目前预测声振系统的主要方法之一，适用于分析50 Hz 以上频率范围的声学系统特性[11]。考虑到等效薄板法的前提是无限大板假设，且增大SEA模型的面积可以提高隔声量预测准确度，因此通过多次模型论证，得知SEA 模型采用5 m×5 m 的规格即可，其隔声量预测模型如图4所示。

多层层合板材料特性参数见表1。

表1 材料特性参数

图4 统计能量法仿真示意图

多层层合板的隔声量计算结果对比如图5至图7所示。

图5 三层层合板隔声量对比（1 mm铝板+1 mm软木+1 mm铝板）

图6 四层层合板隔声量对比（1 mm铝板+1 mm软木+1 mm硬橡胶+1 mm铝板）

图7 五层层合板隔声量对比（1 mm铝板+1 mm胶合板+1 mm硬橡胶+1 mm软木+1 mm铝板）

由图5至图7可以看出，对于三层、四层和五层层合板，当层合板的厚度较小且结构相同时，由等效薄板法得出的结果与SEA 法所得出的结果在进入吻合效应区前的频率范围内基本相同，并且增长率约为6 dB/倍频程，符合板结构在质量控制区内的隔声量增长特性，但在进入吻合效应区后两种方法的结果具有较大误差，因此可以判断，等效薄板法可以用来预测多层层合板在质量控制区内的隔声量；等效薄板法所预测的吻合频率与SEA 仿真结果相比误差较小，误差在1/3个倍频程范围内。

4 结语

本文针对多层层合板的隔声量，在无限大板的假设前提下，通过引入多层层合板弯曲刚度计算公式，提出了用于计算多层层合板隔声量的等效薄板法，通过与统计能量法仿真结果相比较，证明等效薄板法在质量控制区范围内的隔声量预测较为准确，且对吻合频率的预测误差较小，可以作为研究多层层合板隔声性能的方法。