基于量化关联模型的滚动轴承故障评估研究*

谭晓栋，张 勇

(1.电子科技大学 机械与电气工程学院，四川 成都 611731；2.国防科技大学 智能科学学院，湖南 长沙 410000；3.武警警官学院 部队管理系，四川 成都 610213)

0 引 言

滚动轴承在舰船、车辆、航空、化工、电力等领域的动力传动系统中有着广泛的应用。由于长期承受高负荷、高冲击等外部因素的影响，轴承的外圈、内圈和滚动体等部件极易发生故障。据统计，在某些特定的旋转机械系统中，轴承故障占到了系统总故障的44%[1]。因此，及时准确评估出轴承故障程度对减少系统停机时间，对确保系统安全、高效运行具有重要意义[2,3]。

当前，依靠振动数据进行特征提取和状态识别是故障程度评估技术的研究热点[4-9]。DEEPAK P等[10]使用了样条小波检测轴承缺陷，采用了标量指标描述故障严重程度；段晨东等[11]提出了一种基于频率切片小波变换的时频峭度谱分析方法，研究和辨识了滚动轴承的损伤特征频率；CUI等[12]通过分析剥落故障进入滚动体导致的冲击机理，提出了一种新的步进脉冲字典的匹配追踪方法，来定量地评估轴承的故障程度；SINGH等[13]通过组合经验模态分析方法，选择了对故障敏感的固有模态函数(intrinsic mode function, IMF)，优选敏感的IMF散度描述了轴承的故障程度；MOHAMMAD等[14]采用中心极限理论和双谱分析，分别提取了故障状态指标和故障辨识指标，使用改进组合经验模态分析方法实现了对轴承故障的定量诊断；程军圣等[15]使用基于均方根的早期有限样本判定方法(limited feature select sample, LFSS)，选择了滚动轴承故障样本，并通过改进Binary Bat Algorithm(FSBBA)算法提取了性能退化特征，综合LFSS与FSBBA构建了滚动轴承在线故障状态评估模型，从故障数据源和特征提取的层面提高了故障状态评估的精度；张成龙等[16]使用自回归时序模型，提取了故障信号特征，将其作为自联想神经网络的输入，继而辅助滚动轴承故障程度评估；王恒等[17]构造了分层狄利克雷过程更新故障模型结构，获得了设备退化状态动态转移关系，实现了对机械部件的故障等级评估。

为了有效评估数控机床的可靠度，潘立峰[18]深入剖析了数控机床的多性能特征与故障模式之间的关联关系，构建了机床性能特征与故障强弱的关联模型；陈昆弘[19]使用了递归定量分析法提取了滚动轴承的故障特征，建立了基于变量预测模型的故障与特征的定量关联模型，继而指导故障诊断；LIU Yu-mei等[20]使用扩展经验模态分解了轴承运行状态的物元模型，使用本征模函数作为物元模型的特征函数，根据轴承当前健康状态与特征的关联程度，分析了其定性及定量的性能退化过程；杨志淳等[21]构建了配电变压器运行状态评价指标体系，对指标状态量进行了模糊二元量化，利用模糊Apriori算法，挖掘了指标状态量与故障之间的关联关系，提取了诱导变压器故障的关键状态。

综上所述，上述方法主要从特征提取、状态识别等环节独立研究其对结果精度的影响。然而，轴承的故障信号特点是非线性、非平稳，信号不仅微弱、调制性强，而且其频带大多比较宽，受复杂工况等影响，滚动轴承故障信号常常湮没在背景噪声中。即使采用相同数据源信号，不同状态指标对故障程度灵敏度也呈现较大差异。此外，由于滚动轴承的独特功能结构和运动特点，不种类型故障的传播方式和路径不尽相同，导致不同测点监测的故障信息呈现较大差异，很难用精确的数学模型直接描述故障严重程度。

因此，为了提高故障程度评估的准确性，有必要从监测故障的测点、故障状态指标提取及评估模型3个方面，综合分析其与故障程度间的复杂关系。

本文提出一种量化关联模型的滚动轴承故障程度评估技术，使用部署在设备上的多元测点，采集滚动轴承不同故障严重程度下的数据，计算不同故障程度下的指标；建立多元测点、状态指标与故障程度间的量化关联模型，分析计算在多元测点和状态指标下的故障程度评估结果；以评估结果的均方根误差为目标，优化选择适合滚动体故障、内环故障、外环故障3种类型的状态指标和评估模型，进而为精确量化评估滚动轴承故障程度提供有效的数据和模型支撑。

1 量化关联模型

量化关联模型主要用来建立故障程度与多个测点采集的数据源、状态指标间的函数关系。定义量化的故障程度y为因变量，测点数据的函数φ为自变量，建立模型[22]如下：

(1)

根据系统中测点的数量，可以有针对性地设置回归模型。如系统中存在2个测点，则可以设置为如下6种量化关联模型：

(1)只考虑测点t1的线性关联模型M1：

(2)

(2)只考虑测点t2的线性关联模型M2：

(3)

(3)只考虑测点t1的2次多项式关联模型M3：

(4)

(4)只考虑测点t2的2次多项式关联模型M4：

(5)

(5)同时考虑测点t1和t2的线性关联模型M5：

(6)

(6)同时考虑测点t1和t2的2次多项式关联模型M6：

(7)

对于模型参数的求解，往往需要多个样本进行训练。令Ns个训练样本观测值向量矩阵X为：

(8)

式中：Ns—观测值数目；NT—监控故障变化的测点数目；φ(fi)—故障程度与状态指标的关系函数。

模型系数通过训练样本的观测值向量矩阵X，和训练样本对应的真实故障程度向量Y来计算：

B=(XTX)-1XTY

(9)

式中：X—观测值向量矩阵；Y—训练样本对应的真实故障程度向量。

待评估数据样本评估出的故障程度为：

(10)

2 故障评估策略

基于量化关联模型的故障程度评估方法，其主要思想是将已知故障程度的多元测点数据分为训练样本和测试样本，使用训练样本计算不同故障程度评估模型的参数，使用测试样本对比各个评估模型在不同故障程度下评估均方根误差的大小，进而选择出适合不同故障类型的故障程度评估模型和状态指标。

基于量化关联模型的故障评估流程如图1所示。

图1 基于量化关联模型的故障评估流程

故障评估详细步骤如下：

(1)故障程度模拟与注入。通过软件仿真或者硬件加工等方式，模拟不同严重程度故障；

(2)采集多元数据。根据系统监控要求，在系统内外部设置多个测点，采集异常故障信号；

(3)构建故障状态指标向量。采用WANG D、ZHANG B、LAXMIKANT S等[23-25]介绍的30个故障状态指标计算方法，构建故障状态指标矩阵如下：

(11)

式中：Fn—第n个状态指标矩阵；φi—第i个状态指标的计算函数；N—样本总数；NT—部署的测点总数；ojk—在第j个样本中第k个测点采集的数据。

(4)构建故障程度评估模型。根据测点数目，使用式(8)设定可供选择的多元回归评估模型；

(5)计算测试样本的故障程度评估结果。使用式(9)计算训练样本对应的故障程度评估模型系数矩阵为：

(12)

式中：(Bij)train—使用第i个模型第j个状态指标获得的训练样本对应的评估模型系数矩阵；(Xij)train—针对第i个模型使用第j个指标计算的训练样本观测值矩阵；Ytrain—训练样本真实的故障程度向量。

(6)计算测试样本的故障程度评估均方根矩阵。使用式(11)计算NM个模型下，采用NF个指标，计算故障程度评估均方根误差矩阵为：

F1F2…FNF

(13)

式中：R—测试样本的故障程度评估均方根矩阵，行对应故障程度模型，列对应状态指标；NM—为故障程度评估模型总数；rij—使用故障程度模型Mi和状态指标Fj进行故障程度评估的均方根误差。

故障程度评估均方根误差采用如下公式：

(14)

(7)优化选择故障评估模型和故障状态指标优化。选择故障评估均方根误差最小对应的评估模型和故障状态指标为：

(15)

式中：M*—最小故障程度评估均方根误差对应的评估模型；F*—最小故障程度评估均方根误差对应的故障状态指标。

根据模型M*的表达式，确定最优的测点集合T*和模型参数B*。

(8)故障程度评估。使用优化的测点T*采集当前状态下的数据；优化的指标F*提取当前数据的故障状态指标，构建观测值向量矩阵；使用式(10)计算当前状态下的故障程度。

3 实验验证

本文采用美国凯斯西储大学公开的滚动轴承故障数据验证所提方法的有效性[26]。

滚动轴承故障模拟实验平台如图2所示。

图2 滚动轴承故障模拟实验台

该实验台包括一个2 hp的电动机(1 hp=746 W)、扭矩传感器、示功器及电气控制装置。实验轴承为6205-2RS JEMSKF型深沟球轴承，电动机的功率为746 W，输入轴转速为1 772 r/min。

试验设置了滚动体故障、内环故障和外环故障3种典型的故障类型，使用电火花加工不同严重程度的故障状态。

为了分析不同测点对故障程度变化的灵敏度，本文分别在电动机风扇端和驱动端的轴承座上方各设置1个加速度传感器，采集故障轴承的振动信号，定义两个测点为t1和t2；振动信号由16通道数据记录仪采集得到，采样频率为12 kHz，驱动端轴承故障还包含采样频率为48 kHz的数据。

针对滚动体故障、内环故障和外环故障3种故障类型，本文设置损伤直径0、0.007 inch、0.014 inch、0.021 inch 4种故障程度状态，每种状态包含3组数据，共计12组数据；任意选择每种故障状态的2组数据，共计8组数据，建立状态评估模型；剩下4组数据进行测试。

笔者利用试验中两个测点t1和t2的采集振动数据，结合第1节定义的6种故障程度评估量化关联模型，同时按照第2节介绍的滚动轴承故障程度评估流程，计算在6种评估模型和30种状态指标下故障评估的均方根误差，进而优选出适应不同故障类型的评估模型和状态指标。

下面分别对滚动体故障、内环故障及外环故障3种故障类型的4种故障程度(正常状态、0.007 inch、0.014 inch及0.021 inch)进行试验研究和方法验证。

3.1 滚动体故障程度评估

随着滚动体故障程度的增大，振动的幅值也有一定程度的增加，在故障的传播、耦合和噪声等影响下，会使得对不同故障严重程度的辨识难度加大。

笔者使用故障状态指标计算方法，提取正常状态、0.007 inch、0.014 inch及0.021 inch 4种滚动体故障严重程度下，t1和t2两个测点采集数据的时域和频域指标。

滚动体故障4种严重程度下的时域指标如图3所示。

从图3中可以看出：对于滚动体故障而言，在17个时域指标中，除了指标F1呈现递减趋势，其他16个时域指标随着故障程度加剧均呈现逐渐增大的趋势。

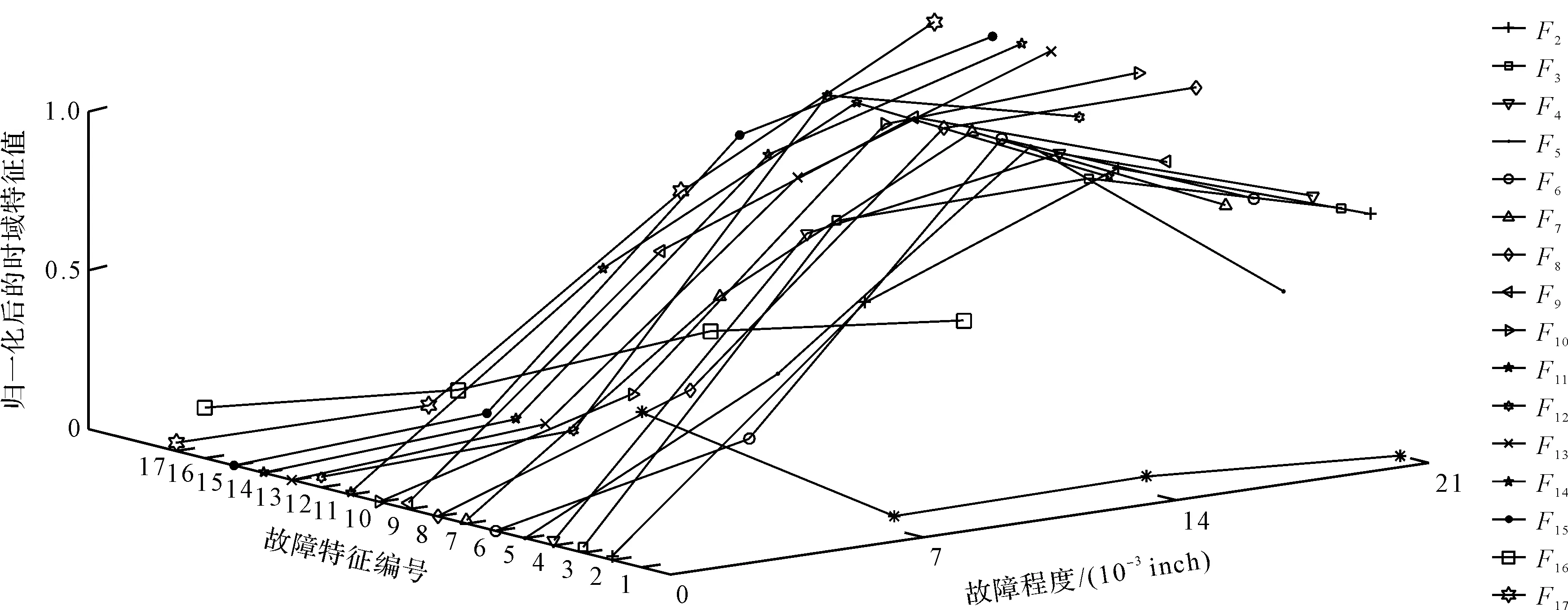
图3 滚动体故障4种严重程度下的时域指标

滚动体故障4种严重程度下的频域指标如图4所示。

图4 滚动体故障4种严重程度下的频域指标X轴—4种故障严重程度；Y轴—时频域故障特征编号；Z轴—归一化的指标值

从图4中可以看出：在剩余的13个频域指标中，指标F18、F20、F23、F28、F30随着故障程度加剧，指标值也相应的增大。

为了衡量各个指标和不同评估模型对滚动体故障程度评估的效果，笔者分别计算采用6种评估模型及30个故障状态指标评估滚动体故障程度的均方根值误差。

滚动体故障程度评估的均方根误差如表1所示。

表1 滚动体故障程度评估的均方根误差

限于篇幅，表1中仅列出了部分时频域指标评估的均方根误差。从表1中可以看出：在17个时域指标中，采用模型M3和指标F3的评估误差的均方根最小为0.003；在13个频域指标中，采用M3模型和故障特征F28，对滚动体故障程度评估的均方根误差最小为0.002 9。

3.2 内环故障程度评估

本文计算正常状态、0.007 inch、0.014 inch及0.021 inch 4种内环故障严重程度下，t1和t2两个测点采集数据的故障状态指标。

内环故障4种严重程度下的时域指标如图5所示。

图5 内环故障4种严重程度下的时域指标

从图5中可以看出，随着内环故障程度加剧，时域指标F11、F17呈现较为明显的增加趋势。

内环故障4种严重程度下的频域指标如图6所示。

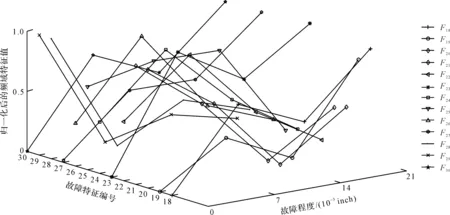
图6 内环故障的4种严重程度下的频域指标

从图6中可以看出：频域指标F18、F19、F22、F23、F27、F30随着内环故障程度加剧，指标值也相应的增大。这说明故障状态指标F11、F17、F18、F19、F22、F23、F27、F30都能较为敏感地感知滚动轴承内环故障程度逐渐增长的过程，只是上述指标对内环故障增长过程的灵敏程度还存在较大区别。

为了进一步找出最能敏感感知内环故障程度增长过程的时频域指标和内环故障程度的评估模型，还需要计算上述指标在6个模型下，评估内环故障程度的均方根误差。

内环故障程度评估的均方根误差如表2所示。

表2 内环故障程度评估的均方根误差

因此，测点t1和t2均包含了内环故障的增长信息；频域特征F22能较好地表征内环故障的严重程度，特征F22与内环故障程度呈现二元二次多项式关系。

3.3 外环故障程度评估

外环故障4种严重程度下的时域指标如图7所示。

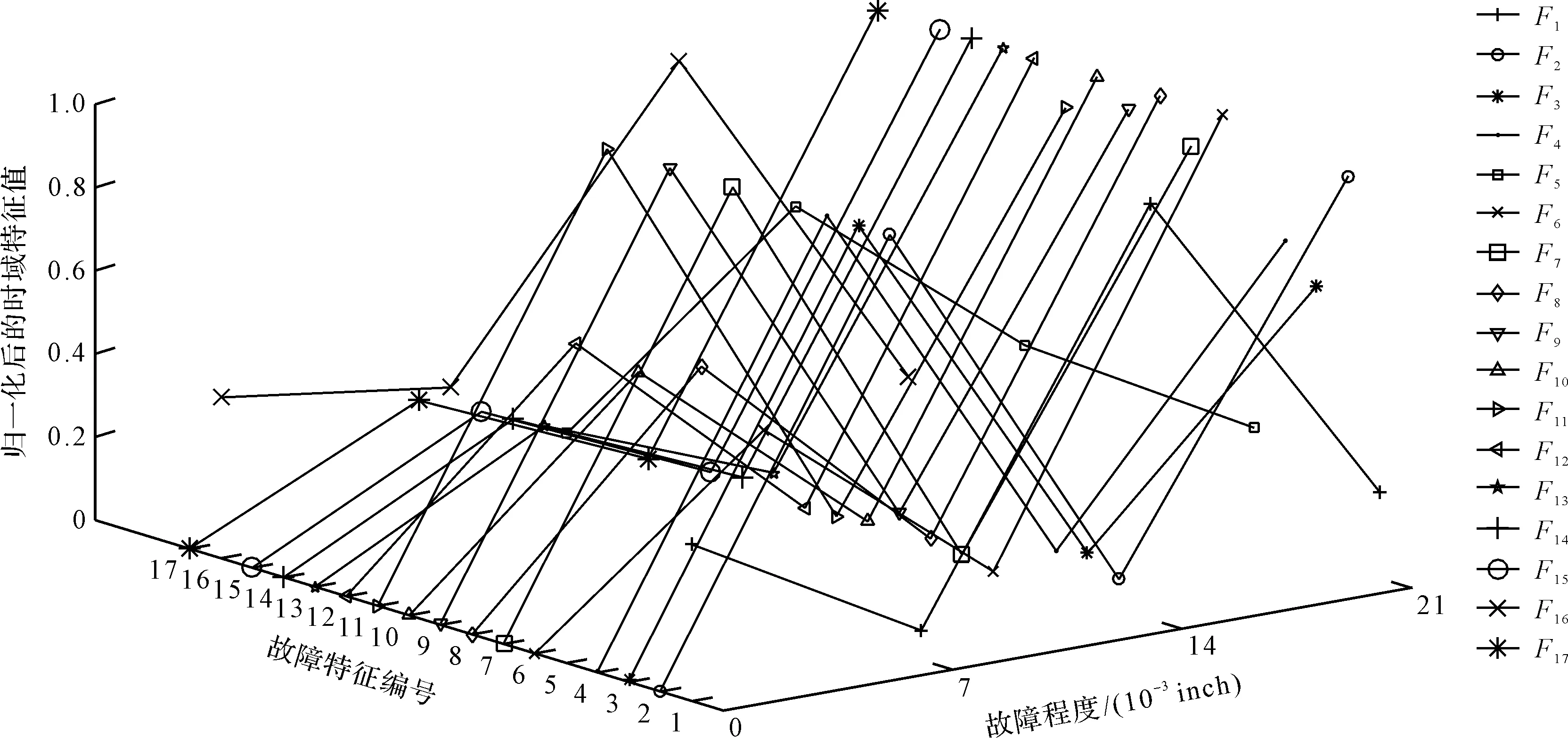
图7 外环故障4种严重程度下的时域指标

从图7中可以看出：除了F1、F5、F16总趋势呈现递减外，其他16个时域指标总趋势随着外环故障程度加剧都逐渐增大。

外环故障4种严重程度下的频域指标如图8所示。

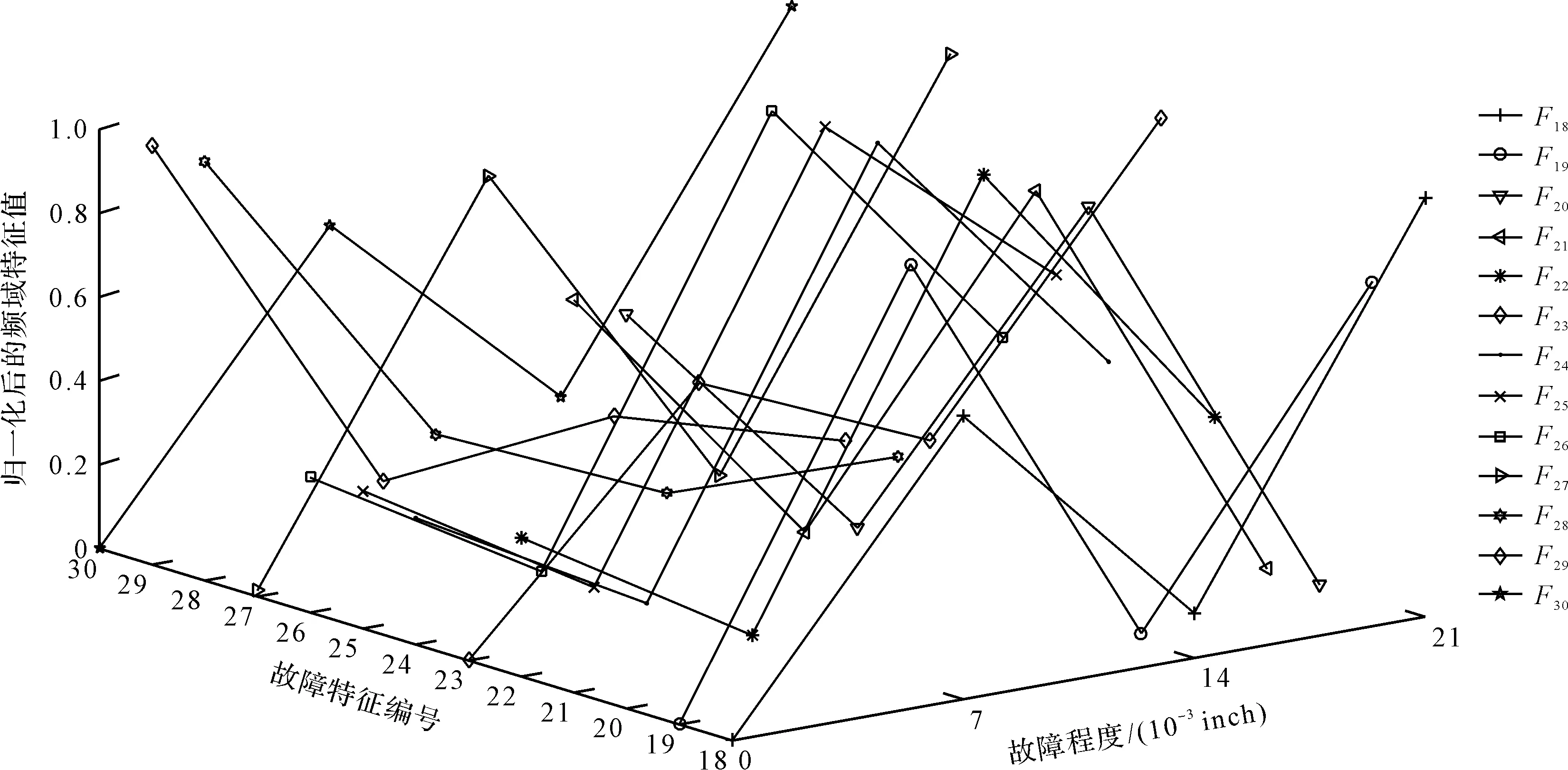
图8 外环故障4种严重程度下的频域指标

从图8中可以看出：在13个频域指标中，F18、F19、F20、F23、F24指标总趋势随着故障程度加剧，指标值也相应的增大。

同理，为了进一步找出最能敏感地感知外环故障增长过程的时频域指标和外环故障程度的评估模型，还需要计算使用上述指标评估在6种评估模型下，评估外环故障程度的均方根误差。

外环故障程度评估的均方根误差如表3所示。

表3 外环故障程度评估的均方根误差

由此可以说明，电动机驱动端的轴承发生了外环故障，使得部署在驱动端基座上的测点t2包含更为丰富的外环故障程度增长信息；特征F24能很好地表征外环故障的严重程度，与外环故障程度呈现一元二次多项式关系。

4 结束语

滚动轴承特定的结构和运动方式使得其故障类型和故障信号的传播方式呈现多样化，不同测点采集的故障信号源和故障状态指标对故障刻画效果和敏感度也呈现较大差别。

本文采用的多元回归模型优化方法，综合考虑了适合滚动体故障、外环故障和内环故障的故障信号源、故障状态指标及评估模型，较传统方法在评估精度和置信度上具有一定优势。

实验分析结果表明：该方法能有效建立滚动轴承故障信号的数据源、指标与评估模型间的定量关联关系；通过分析部署在设备外部的监控数据，可以准确地评估出滚动轴承的故障类型及严重程度，避免了由于数据、指标、模型不统一，给评估结果带来的不确定影响，可以为典型机械部件的测点部署、特征提取和故障评估等，健康状态监控关键技术的有效衔接提供指南。

本文主要采用时频统计特征，作为刻画滚动轴承故障程度的指标，同时使用多元回归线性和非线性模型，融合多个测点数据源。然而，针对不同的机械部件，其功能结构、运动方式、运行工况各具特点，故障的影响和传播方式也会呈现较大区别。

因此，针对不同的运行工况、特定的机械部件及其相应的故障类型，还需从在指标参数选择及评估模型上进一步拓展研究；同时，模型训练和故障程度评估的效率会因为故障数据的增多而有所降低，因此在后期的研究工作中，笔者将综合利用各种优化算法，提高在大数据情况下的模型训练效率和评估效率。