新型带反浪弧浮箱式防波堤消浪特性的数值和试验研究

王晓亮，陈永焜，刘 勇，王兴刚

(1.中国海洋大学 工程学院，青岛 266000；2.南京水利科学研究院，南京 210024)

防波堤对于抵御外海波浪，保证港池内水域平稳、保护海岸基础设施等具有重要作用。传统型式的防波堤可以很好地掩护堤后水域，但是面临着工程造价高、施工难度较大等问题。近年来，浮式防波堤由于具有对地基承载力要求低，造价较低、施工与拆除方便以及有利于水体交换等优点，引起广泛关注。

许多学者针对浮式防波堤的水动力特性开展了深入研究。Rahman等[1]基于VOF法建立了浮式防波堤在波浪作用下的非线性动力学模型，对垂直和倾斜锚固时的系泊力进行了数值计算，并通过物理模型试验进行了验证，发现所建立的数值模型能较好地模拟浮体的水动力特性和系泊力。Zhao等[2]基于CIP方法建立了极端波浪与浮体相互作用的数值模型，通过系列物理模型试验验证了该数值模型，并系统分析了越浪对浮体运动的影响。Ren等[3]通过SPH方法将不同吃水深度浮体的数值模拟结果与相应固定结构的数值模拟结果进行比较，系统分析了浮体的相对长度和密度对浮体水动力特性的影响。杨会利等[4]通过物理模型试验研究了规则波作用下新型应急型浮式防波堤结构的消浪效果，结果表明透射系数随着相对宽度、波陡及相对水深的增大而减小。Christensen等[5]通过物理模型试验研究了浮箱、带有翼板浮箱和带翼板与多孔介质浮箱等三种浮式防波堤的运动阻尼，研究发现：翼板可以有效抑制浮式防波堤的运动响应，带翼板和多孔介质浮箱可以有效降低波浪反射和透射。Ji等[6]通过物理模型试验研究了双排浮式防波堤的反射系数、运动响应和系泊力，并将其与单排浮式防波堤的水动力特性进行了对比，发现双排浮式防波堤能够更有效地耗散波浪能量。Liu等[7]使用开源软件DualSPHysics数值研究了浮式防波堤密度、吃水深度、水体密度和波浪条件等对波浪耗散性能的影响。结果表明吃水深度和波浪参数是浮式防波堤水动力性能的主要影响因素，而防波堤密度和水体密度的影响很小。张昊等[8]数值研究了浮堤宽度、吃水、重心位置和锚链预张力对箱型浮式防波堤透射系数的影响，结果表明增加箱型浮堤的宽度和吃水可以减小透射系数。

为提高传统直立式防波堤的掩护效果，学者们提出设置反弧形胸墙，并对其性能进行了研究。肖阳[9]通过三维模型试验研究了波浪对带反弧面防波堤的作用，表明反弧面具有较好的力学特性。李雪艳等[10-11]通过数值模拟和物理模型试验研究了波浪对弧形胸墙的作用，研究发现：圆弧半径越大，胸墙所受的波浪力越大。吴素舒等[12]通过模型试验研究了带引导式弧形胸墙防波堤的越浪量，结果表明：相比于直立式胸墙，弧形胸墙可以有效降低越浪量。受传统防波堤弧形胸墙的启发，本文提出一种带有反浪弧的新型浮箱式防波堤，并通过数值和试验方法研究新型防波堤的消浪特性。

本文选择光滑粒子流体动力学(Smoothed Particle Hydrodynamics，SPH)对带反浪弧浮箱式防波堤的水动力特性进行数值分析。SPH方法是一种由Lucy[13]、Gingold和Monaghan[14]提出的无网格拉格朗日粒子法，最初由Monaghan[15]于1994年推广到解决自由液面的水动力问题中，在处理流体大变形和结构物剧烈运动问题时具有独特优势。目前，SPH方法已被广泛应用到海洋工程问题中，例如，液舱晃荡[16]、船体入水[17-18]、防波堤消浪[19-20]、波流耦合[21-22]和浮体结构[23]等。传统SPH方法具有压力振荡的缺点，Antuono[24]针对这一问题提出了δ-SPH模型，主要通过在连续性方程中加入耗散项，从而耗散粒子内能，减少粒子压力的高频振荡。已有研究表明，δ-SPH模型具有可靠、有效和准确的优点[23]。本文将建立波浪与浮箱式防波堤相互作用的δ-SPH数值模型，开展物理模型试验对数值结果进行验证，并通过数值算例分析带反浪弧形浮箱式防波堤的水动力特性，研究结果可为工程设计等提供重要参考。

1 基于δ-SPH方法的数值模型

1.1 控制方程

在δ-SPH数值模型中将流体视为有粘、弱可压缩的连续介质，选择拉格朗日形式的Navier-Stokes方程为控制方程，其形式如下

(1)

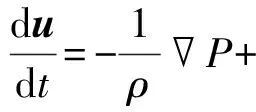
(2)

式中：u为流体速度；ρ为流体的密度；P、g分别为流体的压强和重力加速度；ϑ为流体粘性项，ϑ=▽τ/ρ，τ为剪切应力。

压力P和密度ρ之间的关系，可以通过以下状态方程表示

(3)

式中：ρ0为流体初始密度，取值为1 000 kg/m3；c0为人工声速。

利用δ-SPH方法对控制方程进行离散，可得

(4)

(5)

由于流体的弱可压缩性，在模拟冲击问题时会出现压力震荡现象，为避免压力震荡，在动量方程右侧第三项中，使用Monghan等[15]提出的人工粘性项来代替流体真实粘性

(6)

(7)

连续性方程中右侧第二项为密度耗散项，可以进一步耗散粒子内能和减少粒子压力的高频振动，δ为耗散项系数，其取值一般固定为0.1；ψij由密度梯度决定，其表达式为

(8)

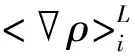
(9)

(10)

在SPH方法中，流体运动遵循牛顿流体力学控制方程，采用核近似法和粒子近似法对控制方程进行离散，给出了SPH形式下的控制方程，利用四阶龙格库塔法求解粒子的密度、位置、压强和速度等属性值[19]。

1.2 数值造波与消波

为避免波浪在造波板处产生的二次反射对模拟结果造成影响，本文使用动量源造波方法[25]进行造波，动量源项通过下式计算

(11)

式中：κ=20/w2，w为造波源宽度；ω为波浪圆频率；D为源函数量，可表示为

(12)

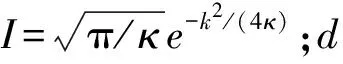
在数值水槽两端各设置一个阻尼消波层来消除固壁边界反射的影响[26]，将人工阻尼项加入到阻尼层内的动量方程中，其表达形式为

(13)

式中：Ls为消波区的宽度；x0为消波区入口处的横坐标。

1.3 浮体的运动响应计算

根据牛顿运动定律，带反浪弧浮箱式防波堤的运动方程和角运动方程分别为

(14)

(15)

式中：V和ξ分别为质心的线速度和角速度；M和I分别为物体的质量和转动惯量；Ff-s为作用在物体上的波浪力；Tf-s为作用在质心上的波浪力力矩；Ft为系泊力；Tt为系泊力的力矩。Ff-s和Tf-s计算如下

(16)

(17)

1.4 锚链的数值分析

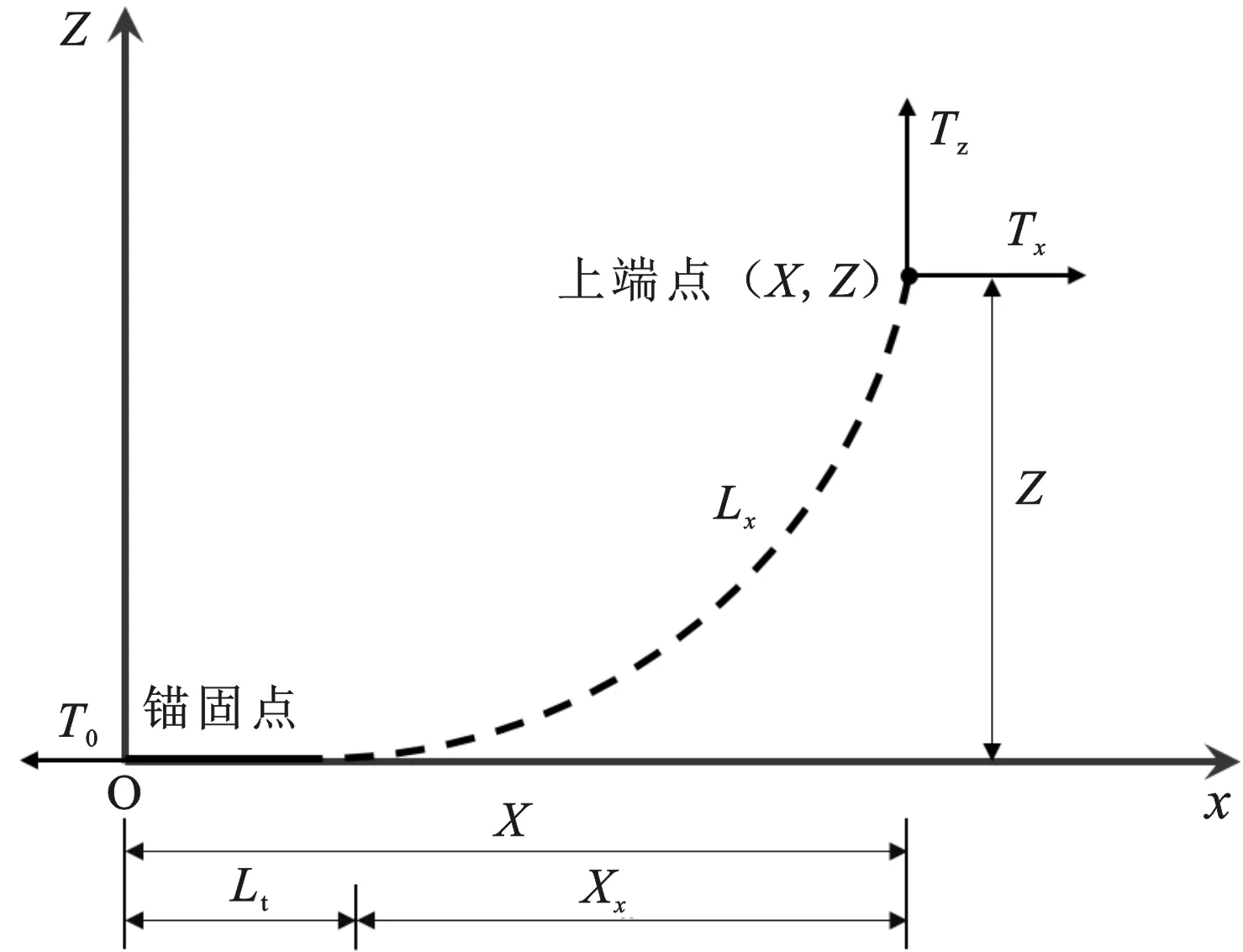
图1 锚链部分拖地示意图Fig.1 Sketch of the mooring chain in partly touchdown state

浮式防波堤的锚链采用悬链线理论[27]进行模拟。根据浮体在波浪作用下的运动情况，将锚链分为三种状态：(1)锚链部分拖地状态；(2)锚链无拖地长度的非伸直状态；(3)锚链拉伸状态。

定义锚链水中重量为wc，拖地长度为Lt，悬起长度为Lx，总长度为S=Lt+Lx，锚链在x轴的投影长度为X，悬起部分在x轴的投影长度为Xx，在z轴的投影长度为Z，锚链最低点所受水平力为T0，锚链上端点所受水平力为Tx，锚链上端点所受垂向力为Tz，故锚链所受的力为Tx和Tz的合力。

(1)锚链部分拖地状态。

图1为锚链部分拖地状态示意图，该状态下的锚链力计算公式如下

(18)

式中：ɑ=Tx/wc；b=wcXx/Tx。

(2)锚链无拖地长度的非伸直状态。

图2为锚链无拖地长度的非伸直状态示意图，该状态下的锚链力计算公式如下

(19)

式中：ɑ=X/b；m= ɑ(1-e-b)/(L-Z)。

(3)锚链拉伸状态。

图3为锚链拉伸状态示意图，该状态下的锚链力计算公式如下

(20)

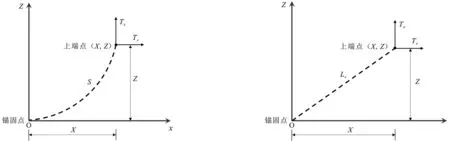
上述式(18)和(19)为非线性方程组，本文采用二分法迭代求解。

2 物理模型试验

2.1 模型设计

本试验在中国海洋大学山东省海洋工程重点实验室的波浪水槽中进行，水槽长60.0 m、宽3.0 m、深1.5 m，水槽首端安装推板造波系统，尾端布置消浪网，可生成不同波高、周期组合的稳定波列。采用薄壁玻璃墙将波浪水槽分为两个通道，两个通道的宽度分别为2.2 m 和0.8 m，模型试验在0.8 m宽的水道中进行。试验中考虑传统矩形浮箱和新型带反浪弧浮箱两种结构，浮箱模型通过锚链锚泊在距离造波机35.15 m处位置，锚链由不锈钢制成，总长度为0.62 m，刚度为2.6 N/mm。浮式防波堤模型在水槽中的具体布置见图4和图5。

试验中的浮箱采用重力相似设计模型，比尺为1：25。模型利用有机玻璃材料制成，内部采用铅块配重，配重后吃水深度为0.15 m，矩形浮箱模型的总质量和惯性矩分别为55.4 kg和2.208 kg·m2；带反浪弧浮箱模型的总质量和惯性矩分别为55.4 kg和2.475 kg·m2。两种模型的实物照片和具体尺寸见图6和图7。

2.2 试验工况

综合考虑实际工程中的典型工况和实验室水槽尺寸及造波能力，确定模型试验所采用的波高、周期组合。试验水深h=0.514 m，采用17种试验组次和两种结构的组合，共计34种工况，具体的试验工况见表1。

表1 浮箱式防波堤模型试验工况Tab.1 Model test conditions of pontoon breakwater

2.3 试验数据采集与分析

试验前率定所有的测量仪器，确保测量仪器正常使用且精准测量。

试验过程中，测量记录浮式防波堤附近的波面变化和结构运动响应，用于验证数值模型的合理性。每组试验重复3遍，取其平均值作为最终结果。

波面变化采用DS30型波高仪测量，波面采集系统的采样间隔为0.02 s，采样时间为50 s。模型前方设置三支波高仪G1、G2和G3，后方设置两支波高仪G4和G5(见图4和图5)。通过合理布置波高仪的间距，采用Goda两点法[28]分离波列，得到反射波高Hr和入射波高Hi，进而计算出反射系数和透射系数，其中：反射系数Kr=Hr/Hi，透射系数Kt=Ht/Hi。

模型运动采用Optotrak Certus三维动态追踪系统测量。如图8所示，每个浮式防波堤上设置9个标记点，每3个标记点组成一个刚体，通过测量刚体的位移信息记录浮式防波堤的运动。

图8 浮箱式防波堤运动响应采集点布置Fig.8 Motion response acquisition arrangement of pontoon breakwater

3 数值模型验证

3.1 数值波浪水槽设置

数值波浪水槽设置见图9，其中：水槽全长22.0 m，距水槽左侧1.3倍波长(L)处设置源造波区域，水槽两端设置阻尼消波层，长度为1.3倍波长，粒子初始间距dx=0.007 m，总数目为25万。浮式防波堤的尺寸与位置、波高仪位置以及数值试验工况同物理模型试验一致。

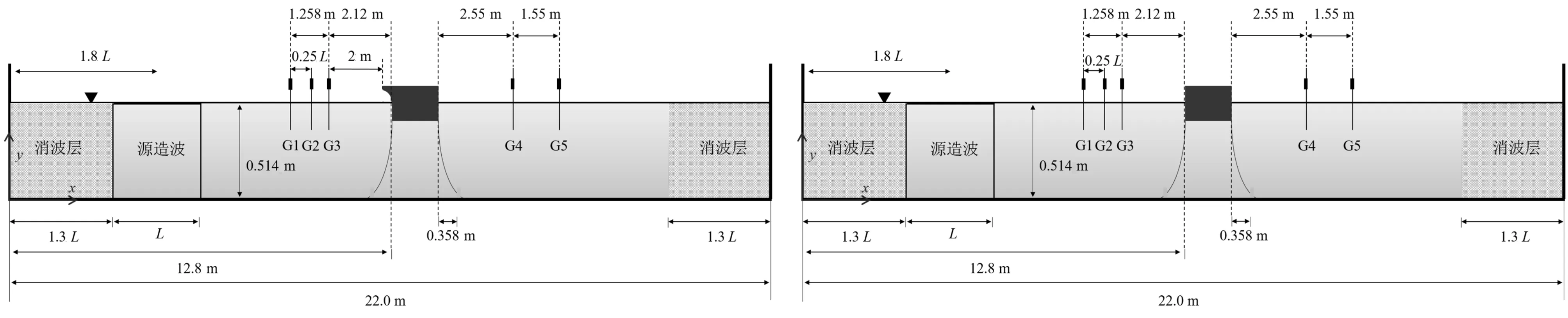
图9 数值波浪水槽设置图Fig.9 Sketch of numerical setup

3.2 数值模型的验证

将带反浪弧浮箱式防波堤和矩形浮箱式防波堤波面变化的数值模拟结果与物理模型试验结果进行对比，图10给出典型工况(H=0.05 m，T=1.4 s)的对比结果。从图10可以看出：数值模拟结果与物理模型试验结果总体符合良好；但是两者之间存在轻微的相位偏移，可能原因是模型试验中浮体与水槽侧壁之间的狭窄缝隙产生的轻微波浪绕射所致。

进一步对比带反浪弧浮箱式防波堤和矩形浮箱式防波堤运动响应的数值模拟结果与模型试验结果。图11给出典型工况下(H=0.05 m，T=1.4 s)防波堤垂荡、横荡和横摇运动的数值模拟结果与模型试验结果对比，可以看出，数值模拟结果与物理模型试验结果符合较好，说明δ-SPH方法可以较好地模拟浮式防波堤的运动。

10-a 带反浪弧浮箱式防波堤

10-b 矩形浮箱式防波堤图10 波面变化的数值模拟结果与物理模型试验结果对比Fig.10 Comparison of numerical and experimental results for the free surface elevations

11-a 带反浪弧浮箱式防波堤

11-b 矩形浮箱式防波堤图11 浮式防波堤垂荡、横荡和横摇运动的数值模拟结果与模型试验结果对比Fig.11 Comparison of numerical and experimental results for the motion of floating breakwater

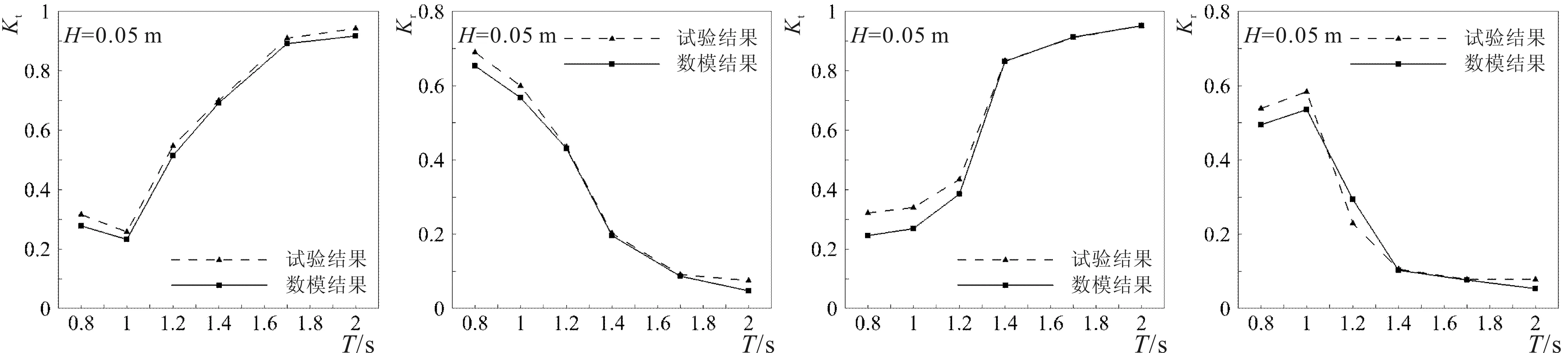
在对比波面演化和浮体运动的数值模拟结果和物理模型试验结果后，图12进一步给出浮式防波堤透射系数Kt和反射系数Kr的数值结果与试验结果对比，可以看出两者总体符合良好。

为验证锚泊系统模拟方法的合理性，将锚链运动形态的数值模拟结果和物理模型试验结果进行对比。图13给出一个典型波浪周期T内(t0=24.079 s时刻到t0+T时刻)，带反浪弧浮箱锚链运动形态的数值与试验结果对比，可以看出数值与试验的锚链形状符合较好，说明了数值模型中锚泊系统模拟方法的合理性。

13-a t=24.079 s

13-b t=24.881 s

13-c t=24.882 s

13-d t=25.783 s

13-e t=25.785 s图13 锚链运动形态的数值与试验结果对比Fig.13 Comparison of numerical and experimental results of chain motion pattern

4 数值分析与讨论

4.1 两种浮式防波堤消浪性能对比

为研究带反浪弧浮箱式防波堤和矩形浮箱式防波堤消浪性能的差异，改变入射波条件，对波浪与两种浮式防波堤的相互作用进行数值模拟，计算条件为：水深h=0.514 m，周期T=0.8 s、1.0 s、1.2 s、1.4 s、1.7 s和2.0 s，波高H=0.02 m、0.05 m和0.10 m；考虑17组波浪和两种结构的组合，共计34种工况。

图14给出带反浪弧浮箱式防波堤和矩形浮箱式防波堤透射系数和反射系数的数值模拟结果对比，可以看出随着波浪周期T的增大，两种浮式防波堤的透射系数Kt逐渐增大，反射系数Kr逐渐减小；当波浪周期T≥ 1.4 s时，带反浪弧浮箱式防波堤的透射系数小于矩形浮箱式防波堤的透射系数，表明新型带反浪弧浮箱式防波堤对较长周期波浪具有更好的掩护效果。特别是当波浪周期T=1.4 s时，带反浪弧结构的透射系数明显小于矩形结构，此时带反浪弧结构的横摇响应远大于方箱结构的横摇响应，并出现峰值，从而有效耗散入射波能量，降低结构的透射系数。

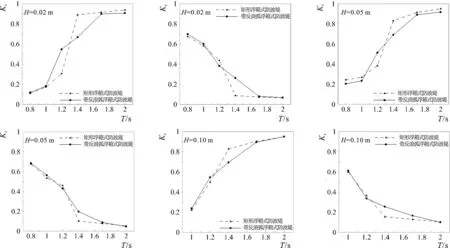
图14 两种浮式防波堤透射系数和反射系数的对比Fig.14 Comparison of transmission coefficient and reflection coefficient of two kinds of floating breakwater

图15给出了带反浪弧浮箱式防波堤和矩形浮箱式防波堤在不同波浪条件下的运动响应对比，可以看出：随着波浪周期的增大，两种浮式防波堤的垂荡和横摇幅值均先增大再减小，横荡幅值逐渐增大。在不同波况下，两种浮式防波堤的垂荡幅值较为接近；横荡运动受到波高的影响，波高越大，二者横荡幅值通常越接近；横摇幅值均随周期变化出现一个峰值，但是二者横摇峰值对应的波浪周期明显不同，分析原因，主要是两种浮式防波堤的横摇共振频率不同。图16给出了两者横摇衰减测试的物理模型试验结果，图中t1～t4分别为两种浮式防波堤横摇处于波谷的时刻，带反浪弧浮箱式防波堤的为3.34 s、4.76 s、6.18 s、7.61 s。t4与t3的差值和t2与t1的差值均约1.4 s，说明共振周期为1.4 s；矩形浮箱式防波堤为2.99 s、4.21 s、6.7 s、7.91 s。t4与t3的差值和t2与t1的差值均约1.2 s，说明共振周期为1.2 s。

4.2 锚链长度的影响分析

通过改变锚链长度，对波浪与带反浪弧浮箱式防波堤和矩形浮箱式防波堤的相互作用进行数值模拟，分析锚链长度对浮式防波堤水动力特性的影响。数值模拟水深h=0.514 m，周期T=1.4 s，波高H=0.05 m和0.10 m，锚链长度S=0.52 m、0.55 m、0.58 m、0.62 m、0.65 m、0.68 m和0.71 m，包括7种锚链长度、2种波况和2种结构的组合，共计28种工况。

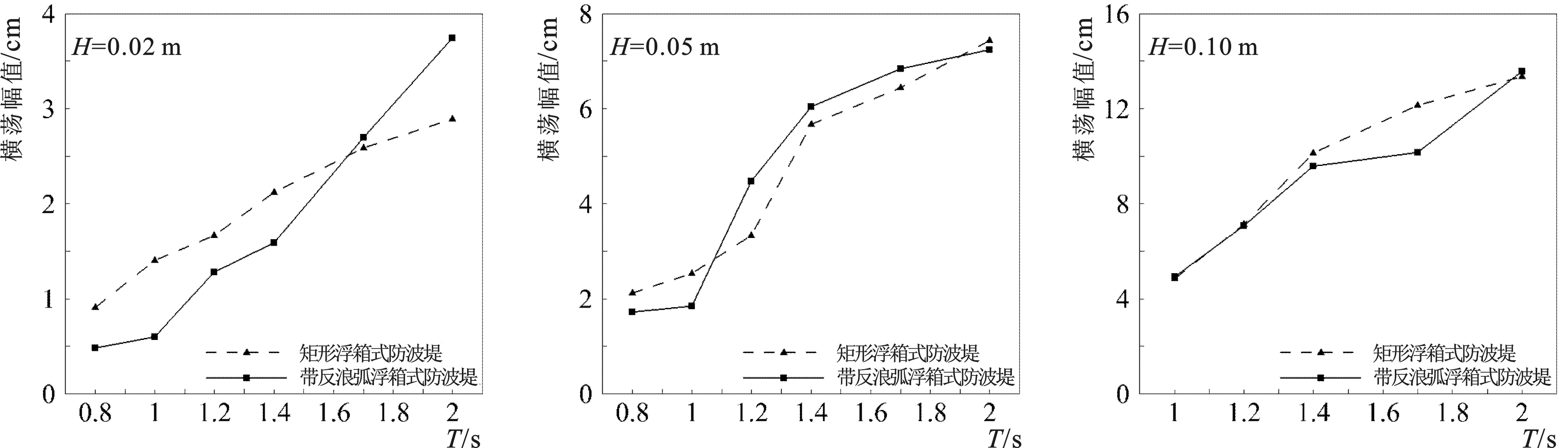
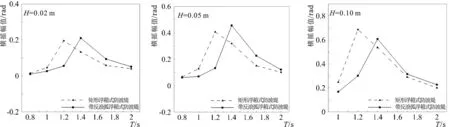
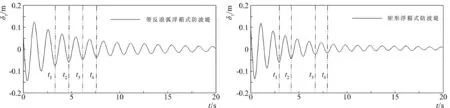
图17给出不同锚链长度对带反浪弧浮箱式防波堤和矩形浮箱式防波堤透射系数Kt的影响，可以看出，随着锚链长度S的增大，两种浮式防波堤的透射系数均呈现减小趋势。当锚链长度S≥0.55 m时，锚链处于拖地状态，此时进一步增加锚链长度对两种浮式防波堤运动响应的影响较小，透射系数的变化也较小。当锚链长度S=0.52 m时，两种浮式防波堤的掩护效果都不理想，这主要是因为波浪与浮体作用后产生的辐射波与透射波叠加的结果。

图18给出不同锚链长度对带反浪弧浮箱式防波堤和矩形浮箱式防波堤运动响应的影响，可以看出：随着锚链长度S的增大，两种浮式防波堤的垂荡与横荡幅值呈现先减小后稳定的趋势，横摇幅值呈现先增大后趋于稳定。当锚链长度S≥ 0.55 m时，锚链处于拖地状态，此时增加锚链长度对浮式防波堤所增加的约束作用有限，使得两种浮式防波堤的运动响应受锚链长度变化的影响较小。

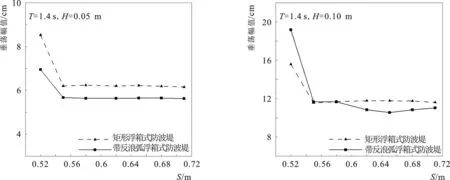
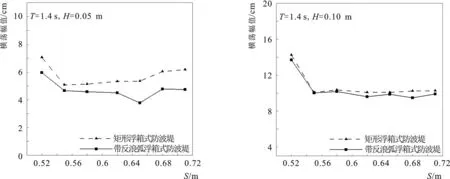
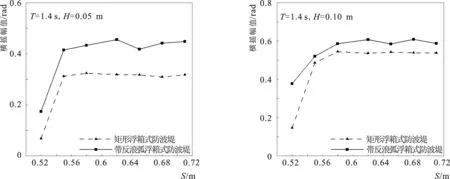
图19给出工况T=1.4 s、H=0.05 m下，带反浪弧浮箱式防波堤和矩形浮箱式防波堤周围的流场变化对比图(从t0=23.176 s时刻到t0+T时刻)，可以看出在波浪作用下，浮式防波堤的运动会使周围水体产生涡旋，涡旋的产生与脱落能够有效耗散波浪能量，提高结构的掩护效果；带反浪弧浮箱式防波堤的运动会在周围水体产生更大范围的涡旋，波能耗散更为显著。

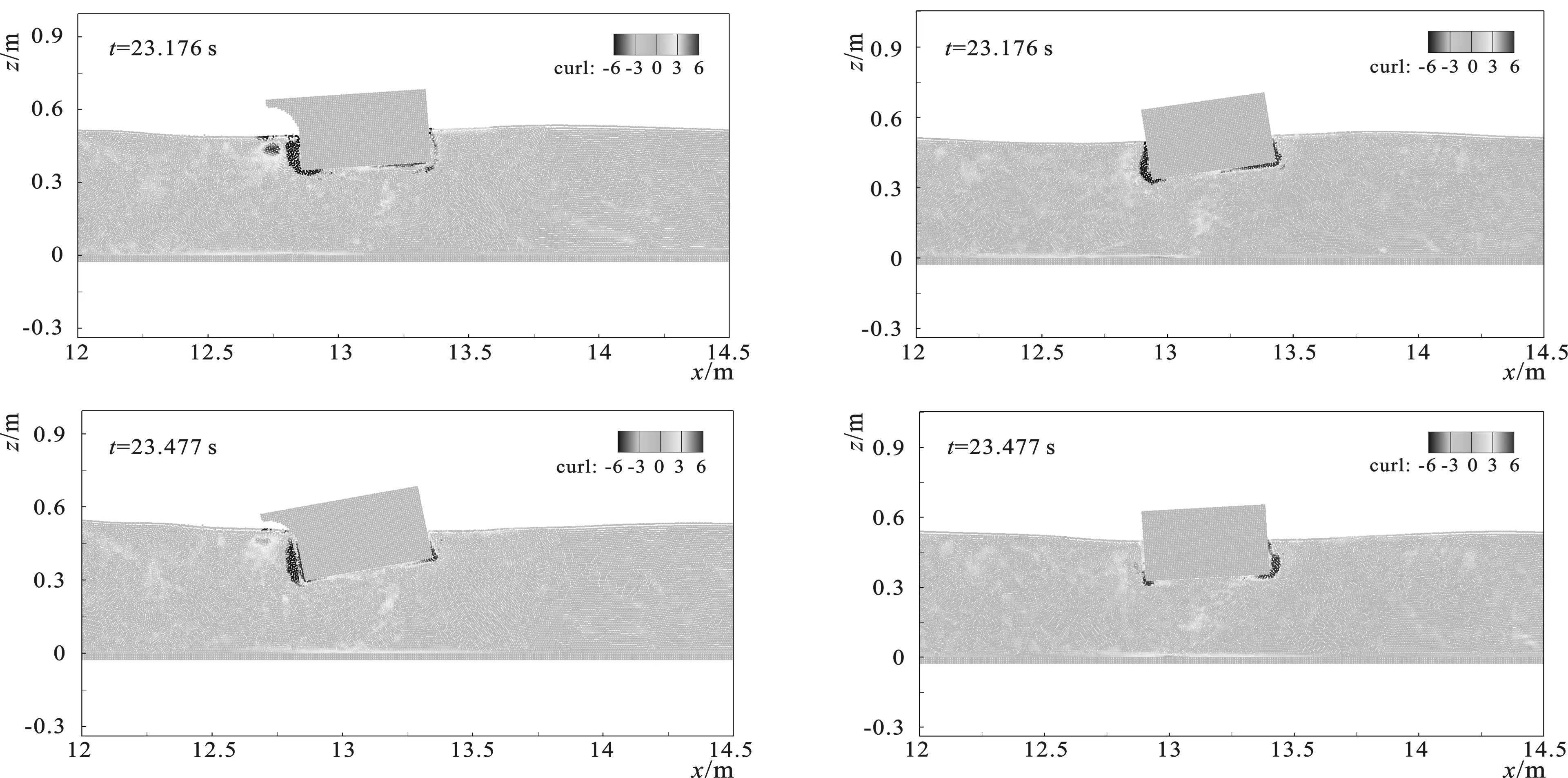
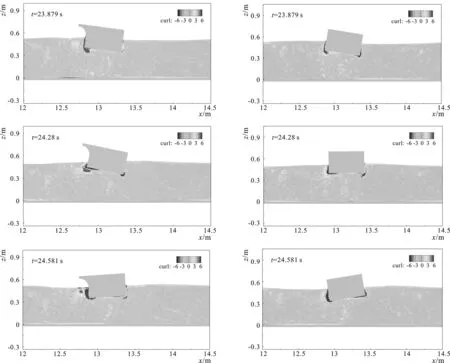
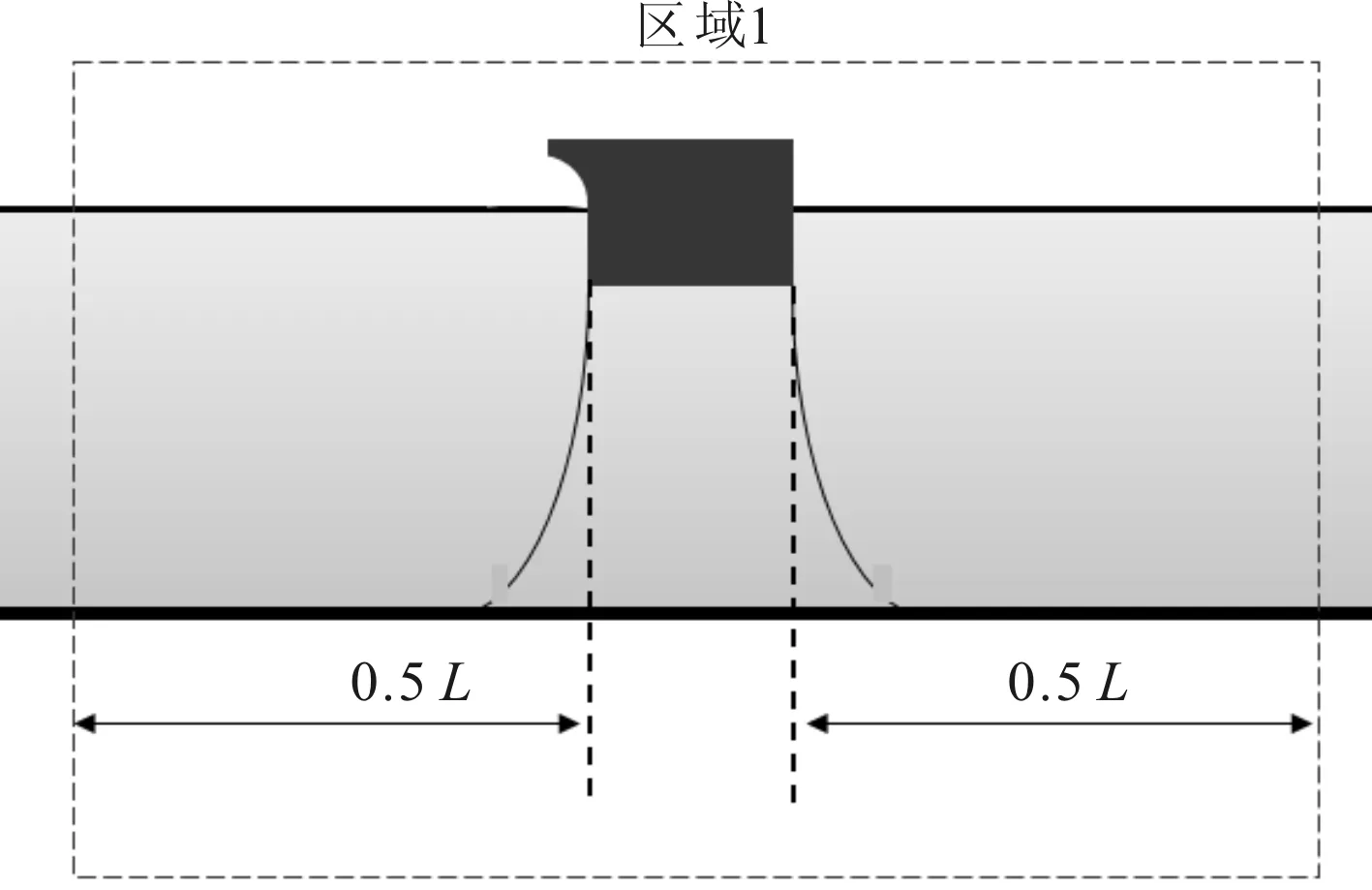
图20 涡量计算区域Fig.20 Vorticity calculation area

4.3 流场特性分析

图21给出工况T=1.4 s、H=0.05 m下，带反浪弧浮箱式防波堤和矩形浮箱式防波堤在区域1(见图20)的涡量和对比，Ω+为正涡量，Ω-为负涡量，∣Ω∣为涡量绝对值(Ω为涡量，Ωi= Σ(mi(ui-uj)/ρi×▽iWij)，逆时针为正)，可以看出带反浪弧浮箱式防波堤运动产生的正涡量大于矩形浮箱式防波堤运动产生的正涡量；带反浪弧浮箱式防波堤运动产生的负涡量变化较大；在波浪与两种浮式防波堤相互作用的过程中，带反浪弧浮箱式防波堤运动产生的总涡量更多，耗散的波浪能量更多。

5 结论

本文基于δ-SPH方法，结合动量源造波法和阻尼消波法，建立了无反射的二维数值波浪水槽，再结合悬链线理论方法，建立了波浪与浮箱式防波堤相互作用的数值模型。开展了波浪与新型带反浪弧浮箱式防波堤相互作用的物理模型试验，利用模型试验结果验证了数值模拟结果的合理性。通过数值算例，对比分析了带反浪弧浮箱式防波堤和矩形浮箱式防波堤的透射系数、反射系数、运动响应及流场特性，探讨了带反浪弧浮箱式防波堤的消浪机理，研究发现：

(1)随着波浪周期的增大，带反浪弧浮箱式防波堤与矩形浮箱式防波堤的透射系数均逐渐增大，反射系数逐渐减小，结果表明，新型带反浪弧浮箱式防波堤对较长周期波浪具有更好的掩护效果。两种浮式防波堤垂荡运动较为接近；横荡运动受到波高的影响，波高越大，二者横荡幅值通常越接近；横摇幅值均随周期变化出现一个峰值，但是二者横摇峰值对应的周期明显不同。

(2)锚链是否拖地对带反浪弧浮箱式防波堤与矩形浮箱式防波堤的消波效果有显著影响。当锚链长度为0.52 m时，锚链为无拖地长度的非伸直状态，此时两种浮式防波堤运动响应幅值和透射系数与锚链部分拖地状态下两种浮式防波堤运动响应幅值和透射系数相差较大；当锚链长度大于0.52 m时，锚链为拖地状态，此时进一步增加锚链长度对两种浮式防波堤运动响应的影响较小，透射系数的变化也较小。

(3)在波浪作用下，带反浪弧浮箱式防波堤的运动会使周围水体产生涡旋，涡旋的产生与脱落能够有效耗散波浪能量，达到较好的消波效果。