圆管支撑钢板仓组合剪力墙抗震性能分析

盖彤彤，于德湖，毛鲁宁，郁有升

(青岛理工大学土木工程学院，青岛 266033)

组合剪力墙是一种新型结构构件，能够有效结合钢与混凝土的性能特点。与钢筋混凝土剪力墙相比，其承载能力、耗能能力以及延性都有所提高。同时具有施工简便、相对经济、自重较轻的优势。目前，组合剪墙的研究主要集中于两种形式：内置钢骨和外置钢板组合剪力墙。Zhang等[1-2]对一字形和T字形钢管束组合剪力墙进行了试验和理论研究，结果表明：该结构的承载力、耗能情况以及延性良好，并且抗震性能优越；石继兵等[3]、伍云天等[4]分别对内置钢板带、内置桁架组合剪力墙进行试验研究，结果表明：内置钢骨在结构破坏时起支撑作用，能够提高结构的承载力并减缓刚度退化；白亮等[5]、王金金等[6]、范重等[7]、林荣深等[8]针对不同剪跨比和轴压比的组合剪力墙进行了试验研究，结果表明：剪跨比会影响结构的破坏形式，同时轴压比过大会降低结构的变形性能，为保证墙体的抗震性能，需根据实际工程选用合适的轴压比和剪跨比。

现针对一种新型组合剪力墙构件——圆管支撑钢板仓组合剪力墙，利用ABAQUS在控制轴压比的条件下，进行低周反复加载数值模拟。改变墙体剪跨比、钢板强度、钢板厚度、轴压比、墙体厚度以及混凝土强度，分析各参数对钢板仓剪力墙抗震性能的影响情况。同时，利用有限元模拟数据对墙体的抗剪承载力计算公式进行拟合，以保证墙体在使用中的安全性和稳定性。

1 ABAQUS建模

1.1 有限元试件设计

圆管支撑钢板仓组合剪力墙由两块钢板和钢质圆管支撑组成仓体，再向仓内浇筑混凝土构成基本单元，如图1所示。其中钢板1截面为卷边槽形，在凹槽内焊接钢质圆管3，钢板2与钢质圆管3对应位置预留圆形孔洞；钢板2搭接在钢板1的凹槽上并焊接而成，已焊于钢板1上的钢质圆管3与钢板2焊接形成钢板仓，最后向仓体内浇筑混凝土，经养护形成圆管支撑钢板仓组合剪力墙。相较于其他类型组合剪力墙，此构造在保证平面外刚度的情况下，可减少焊接量，提高施工效率，同时节约钢材。

为研究不同参数对圆管支撑钢板仓组合剪力墙抗震性能的影响情况，改变墙体的剪跨比、钢板强度、钢板厚度、轴压比、墙体厚度以及混凝土强度。利用有限元软件ABAQUS建立相应模型，对墙体进行变参数分析，建立6组共18个构件，与GBC-1进行对比分析。构件详细设计参数如表1所示。

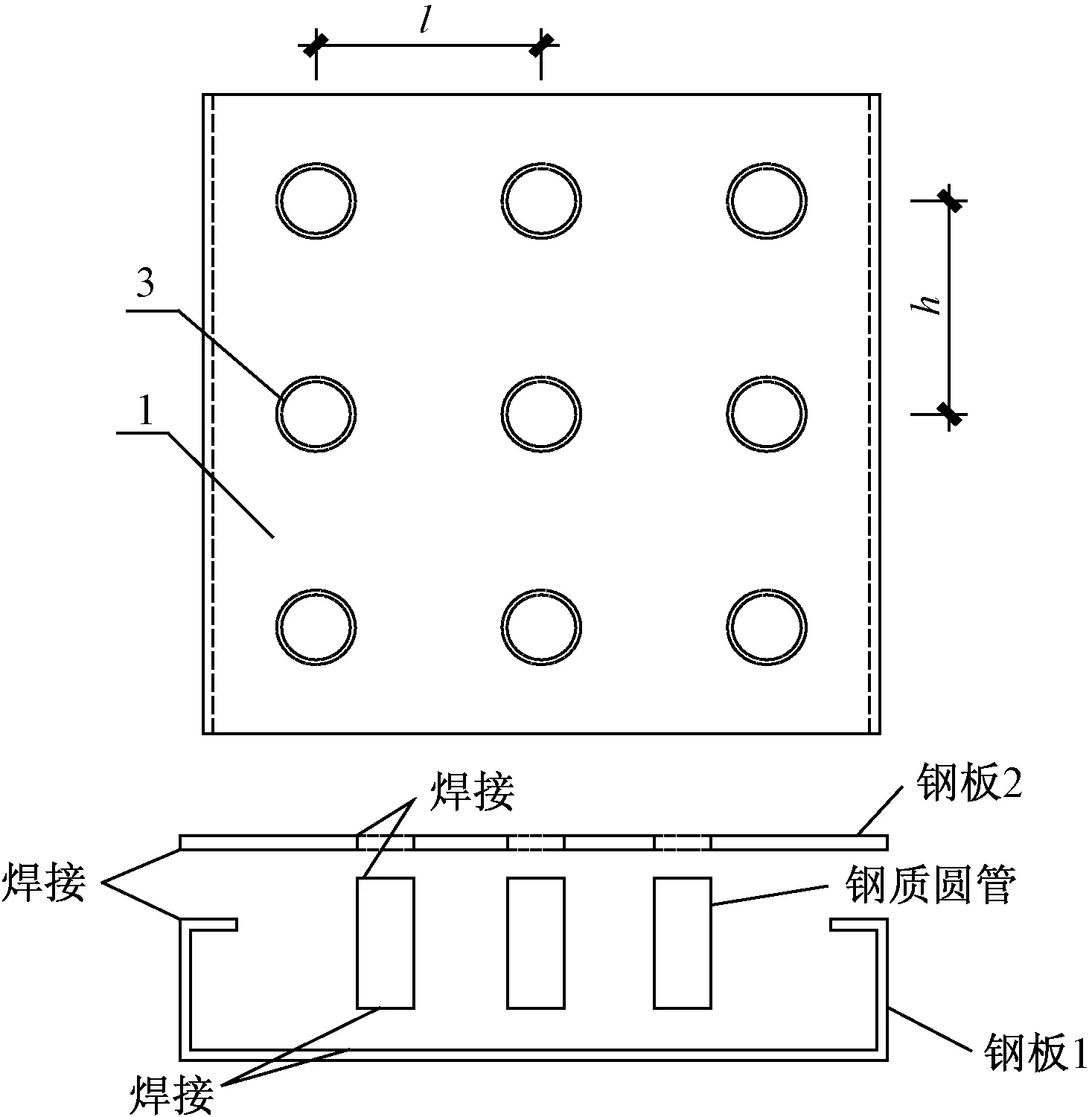
图1 圆管支撑钢板仓组合剪力墙详图Fig.1 Round tube support steel silo combination shear wall detail

表1 各构件详细设计参数Table 1 Detailed design parameters of each component

1.2 材料本构模型

1.2.1 混凝土本构

钢板仓对仓内混凝土有一定约束作用，约束效应系数用ξ表示，采用Han等[9]的混凝土本构模型。

受压本构模型：

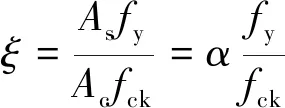
(1)

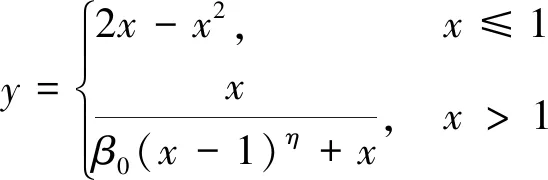
(2)

(3)

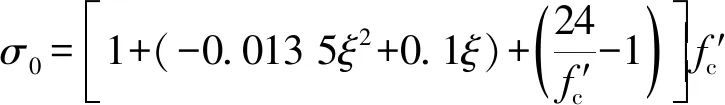
(4)

ε0=εc+800×10-6ξ0.2

(5)

β0=0.5×(2.36×10-5)[0.25+(ξ-0.5)7](f′c)0.5≥0.12

(6)

式中：f′c为混凝土圆柱体轴心抗压承载力；As、Ac分别为钢板和混凝土横截面面积；fy为钢材的极限抗拉强度；fck为混凝土轴心抗压强度标准值；α为横截面含钢率；εc为混凝土峰值压应变；σ、ε分别为核心混凝土压应力、压应变；σ0、ε0分别为核心混凝土峰值压应力、峰值压应变；β0为与ξ有关的变量。

受拉本构模型：

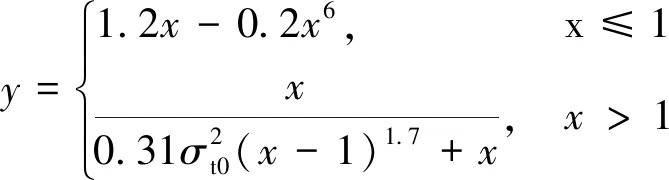
(7)

(8)

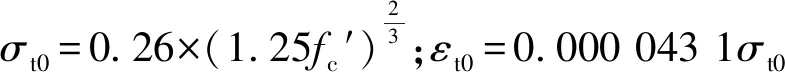
(9)

式中：σt、εt分别为核心混凝土拉应力、拉应变;σt0、εt0分别为核心混凝土峰值拉应力、峰值拉应变。

1.2.2 钢材本构

钢材采用等向弹塑性模型，强化阶段的弹性模量取0.01Es，Es为所用钢材的弹性模量。

1.3 接触模型

外包钢板仓与混凝土的接触由界面法线方向接触和切线方向黏结滑移构成，接触界面法向采用硬接触，切向力模拟采用“罚”摩擦，摩擦因数取 0.4，且界面可以传递剪应力直到剪应力达到临界值，滑动过程界面剪应力保持不变。

组成外包钢板仓钢板太薄，整体刚度小于混凝土，故以混凝土为接触主面。为保证顶部受力均匀，添加一块与横截面等面积的钢盖板，盖板与钢板仓模型采取“tie”约束，两块钢板与圆管也采取“tie”约束。

1.4 单元类型选取及网格划分

钢板仓和仓内混凝土采用八结点线性六面实体单元(C3D8R)，此实体单元可构建任意试件、承载任何荷载，有利于分析试件的受力情况。模型采用较为精细的网格划分以提高数值模拟的准确性。钢板孔洞处采用六面体中性轴扫掠网格划分，规整的网格可优化分析结果。划分情况以GBC-1为例，如图2所示。

图2 墙体网格划分图Fig.2 Wall grid map

1.5 边界条件及加载制度

构件底部完全固定，顶端为自由端，轴向力以均布荷载加载于盖板。先施加轴向荷载，待轴力保持稳定后，再进行水平低周往复加载。水平加载位移随时间逐级增大，加载初期每级增加减少1 mm，屈服后每级增加或减少2.5 mm，每一级循环一次。加载制度如图3所示。

1.6 有限元模型验证

Zhang等[1]针对钢管束组合剪力墙设计了多组原型试件进行拟静力试验，采用本文建模方法建立YZQ-1对应的有限元模型，与试验结果进行对比分析，结果如图4所示。由图4可知，模拟结果峰值荷载增加了1.82%，骨架曲线吻合较好，验证了本文方法的准确性。考虑到有限元模型各项条件为理想状态，而试验采用的材料为非均质，同时试验前误差累计、钢材的初始缺陷均会对墙体产生影响，故数值模拟结果略高于试验。

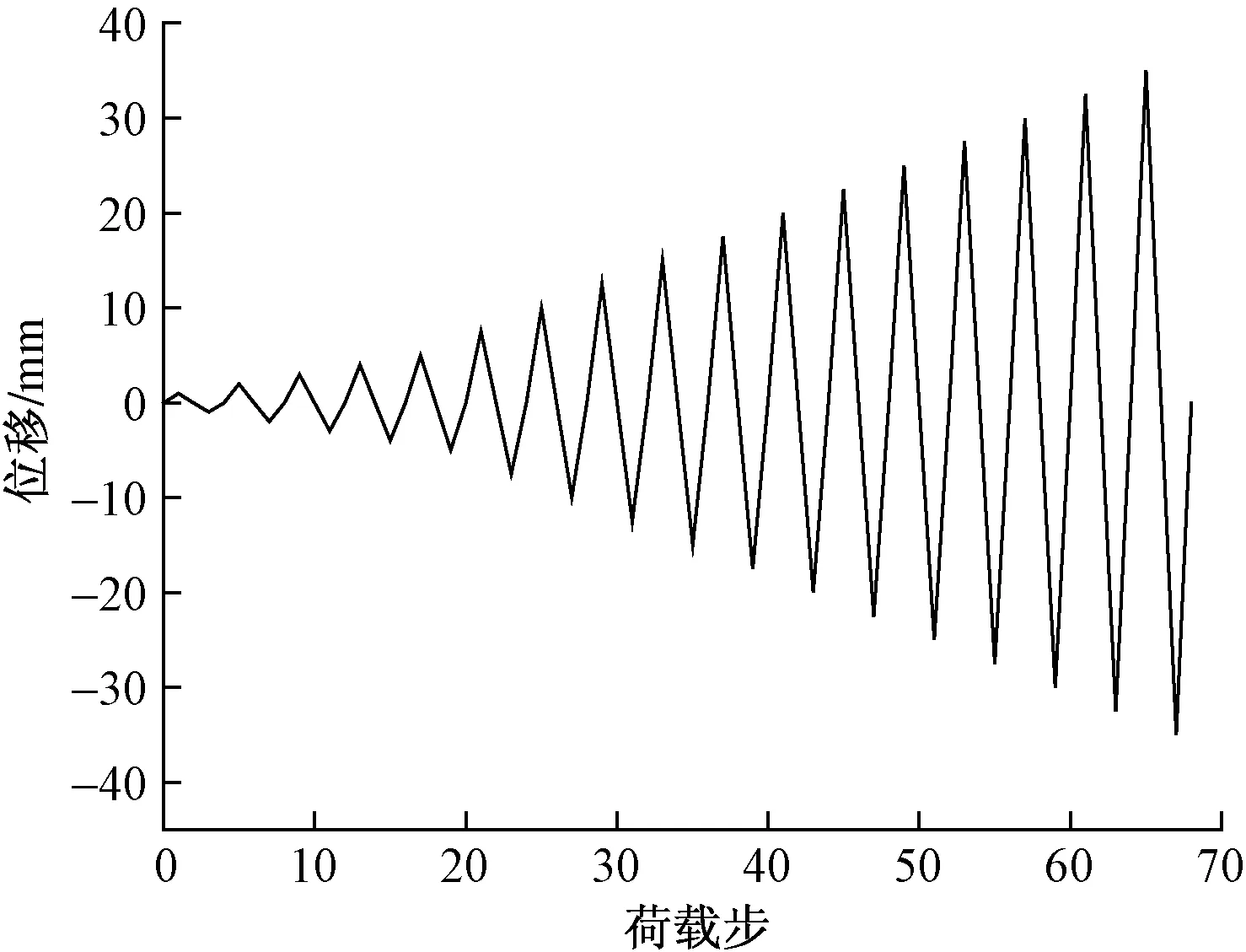
图3 加载制度图Fig.3 Loading system diagram

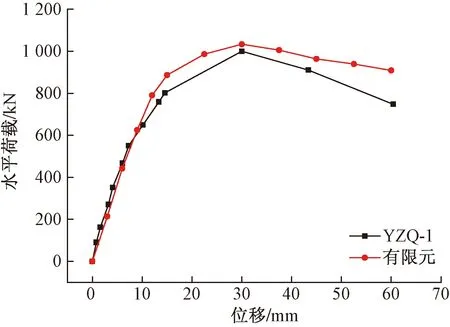
图4 模拟与试验对比图Fig.4 Simulation and test comparison chart

2 有限元模型参数化分析

2.1 剪跨比的影响

改变墙体剪跨比，对构件进行低周反复加载得到滞回曲线如图5所示。由构件的滞回曲线可以看出，剪跨比由1.5增大至1.75、2.0、2.25、2.5时，峰值承载力分别降低了15.39%、25.36%、34.6%、41.88%。随着构件高度增加，墙体向细长柱发展，墙体更易发生失稳破坏，导致构件承载力下降。随着剪跨比增大，构件的极限位移、屈服位移均增大，而构件的初始刚度和延性系数降低，变形能力减弱。

图5 不同剪跨比下构件滞回曲线Fig.5 Hysteresis curve of the member under different shear span ratios

图6 不同钢板仓强度下构件滞回曲线Fig.6 Hysteresis curve of components under different steel silo strength

2.2 钢板强度的影响

改变钢板强度，对构件进行低周反复加载得到滞回曲线如图6所示。由图6可知，钢板强度由Q235增大至Q345、Q390、Q460，墙体峰值承载力分别增加了27.28%、34.01%、48.88%。提高钢板强度能够增大钢板仓对混凝土的约束作用，有效抑制混凝土裂缝的开展，使构件的承载力增大。随着钢板强度提高，构件的极限位移、屈服位移均增大，而构件的初始刚度和延性系数降低，变形能力减弱。

2.3 钢板厚度的影响

改变钢板厚度，对构件进行低周反复加载得到滞回曲线如图7所示。由图7可知，钢板厚度由3 mm增大至4、6、8 mm，峰值承载力分别增长了19.29%、55.69%、91.01%。外包钢板仓为墙体提供主要抗侧刚度，增加钢板厚度可以增大钢板仓对内部混凝土的约束作用，使墙体的峰值承载力提高。随着钢板厚度增大，构件的初始刚度、极限位移均增大，而构件的屈服位移减小，延性系数先增大后减小。钢板厚度为5 mm时，变形能力更强。

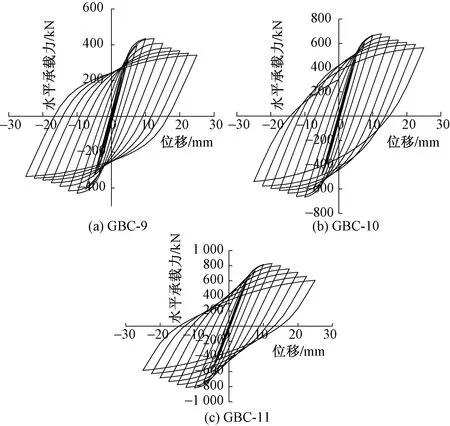
图7 不同钢板仓厚度下构件滞回曲线Fig.7 Hysteresis curve of components under different steel silo thickness

2.4 轴压比的影响

改变轴压比对构件进行低周反复加载得到滞回曲线如图8所示。由图8可知，轴压比小于0.4时，增加轴压比可以使钢板仓与混凝土结合得更加紧密，内置混凝土为钢板仓提供支撑作用，防止钢板仓提前鼓曲失效，同时提高构件的承载能力。轴压比大于0.4时，增加轴压力会使钢板与混凝土逐渐脱离共同工作状态，内置混凝土受压提前开裂，钢板仓失去支撑受载屈曲，构件承载能力随之减小。随着轴压比的增大，构件的初始刚度、极限位移、屈服位移均减小，延性系数降低，变形能力减弱。且轴压比小于0.5时，构件的延性系数变化不明显。

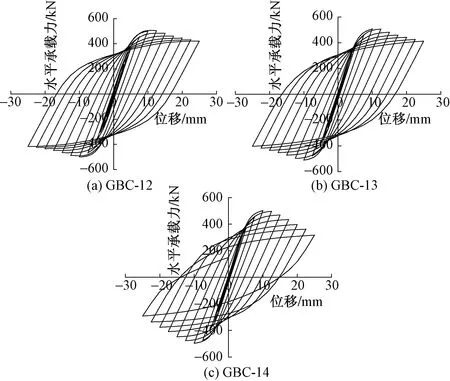
图8 不同轴压比下构件滞回曲线Fig.8 Hysteresis curve of the member under different axial compression ratios

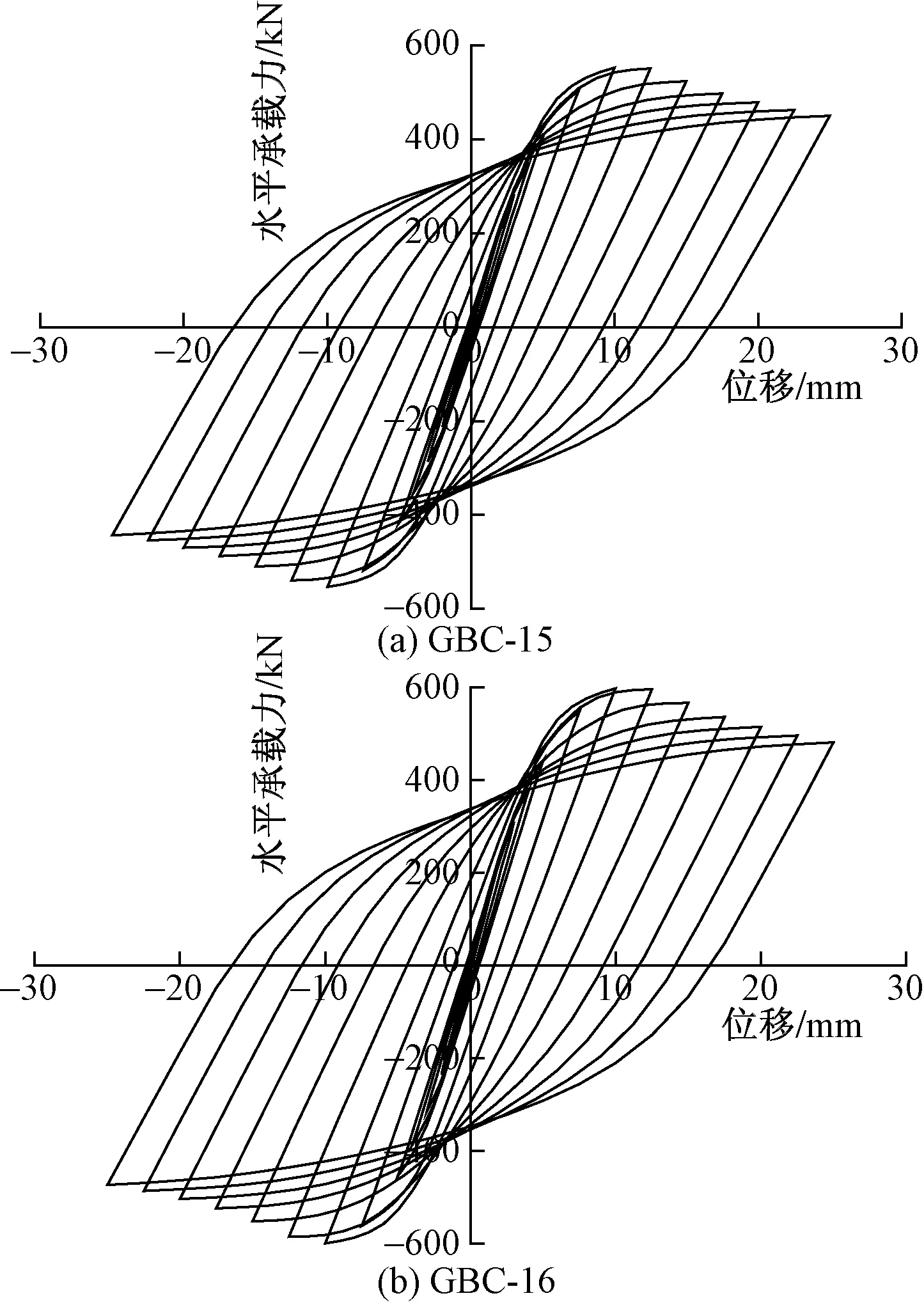
图9 不同墙厚下构件滞回曲线Fig.9 Hysteresis curve of components under different wall thicknesses

2.5 墙体厚度的影响

改变墙体厚度，对构件进行低周反复加载得到滞回曲线如图9所示。由图9可知，控制轴压比为0.4，墙体厚度由120 mm增大至140 mm和160 mm，峰值承载力分别增长了6.47%和15.26%，内置混凝土可以为外包钢板仓提供支撑，提高墙体的承载能力，防止两侧钢板提前鼓曲致使墙体破坏。随着墙体厚度的增大，构件的极限位移、屈服位移均减小，而构件的初始刚度、延性系数均增大，变形能力增强。

2.6 混凝土强度的影响

改变混凝土的强度，对构件进行低周反复加载得到滞回曲线如图10所示。由图10可知，混凝土强度由C30增大至C50、C70，峰值承载力分别增长了20.52%和41.64%。混凝土强度增加使得内置混凝土的抗压能力增强，构件承载能力提高。随着混凝土强度提高，构件的初始刚度和屈服位移增加，而构件的极限位移减小，延性系数降低，变形能力减弱。

图10 不同混凝土强度下构件滞回曲线Fig.10 Hysteresis curve of components under different concrete strengths

2.7 不同参数构件模拟结果

不同参数条件下的构件模拟结果如表2所示。

3 钢板仓组合剪力墙抗剪承载力计算公式分析

3.1 钢板仓组合剪力墙抗剪承载力计算公式的确定

针对提出的钢板仓组合剪力墙，现有的抗剪承载力计算公式不能够直接用于墙体承载力的计算。根据墙体的参数化分析发现，钢板仓组合剪力墙抗剪承载力主要由钢板仓和内置混凝土承担，钢质圆管主要起约束作用，对墙体承载力影响微小，故在计算中暂时忽略不计。同时，轴向力在加载过程中会增进钢板仓与混凝土的共同作用，对墙体承载力有一定的提升作用。故利用叠加法对墙体斜截面承载力进行多项式拟合，可以得到计算公式为

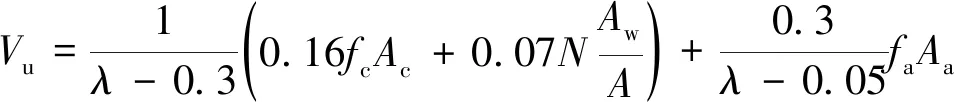
(10)

式(10)中：λ、A、Aw分别为墙体剪跨比、墙体和墙体腹板横截面面积，若墙体为矩形，Aw取1；fa、fc分别为钢板屈服强度设计值、混凝土轴心受压强度设计值；Ac、Aa分别为钢板仓组合剪力墙同一高度下混凝土横截面面积、钢板仓横截面面积。

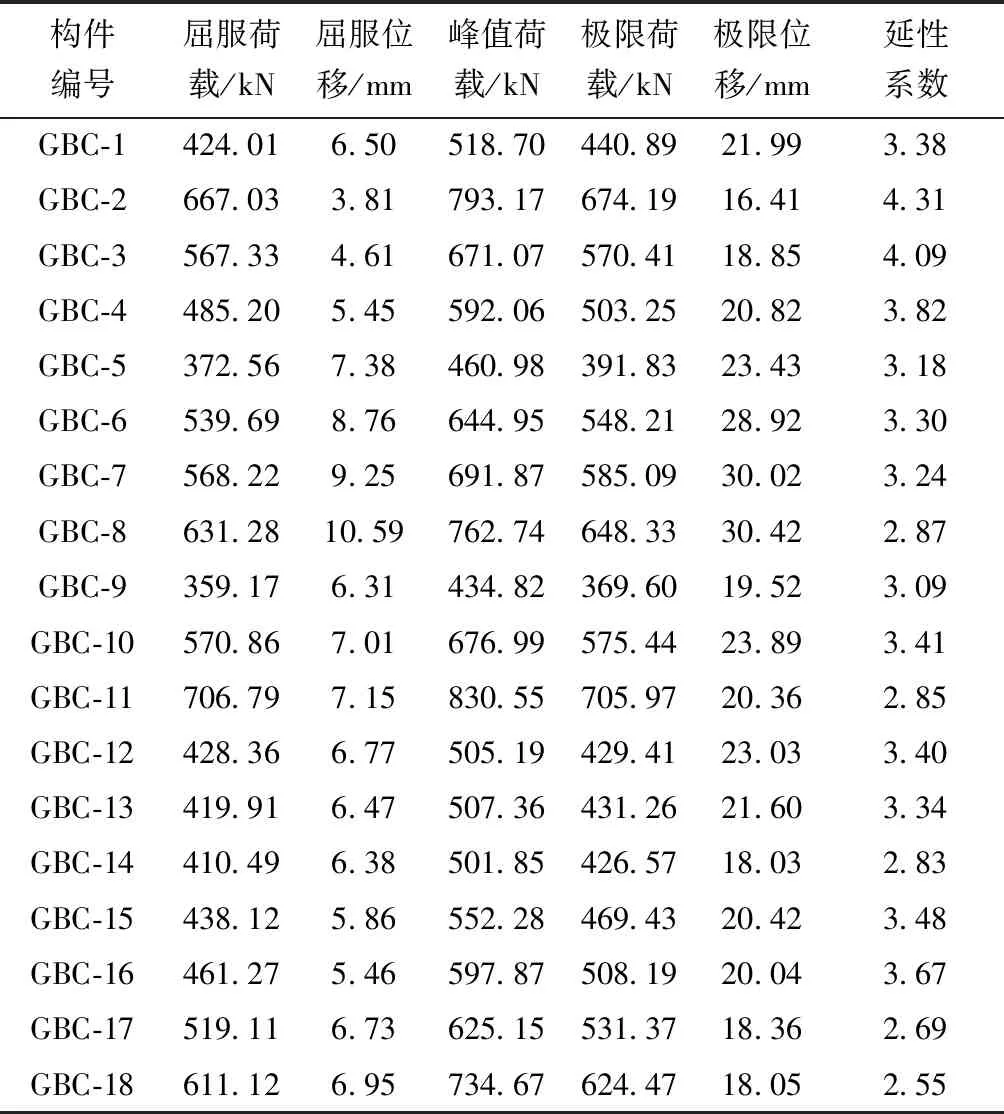
表2 不同参数条件下的构件有限元模拟结果Table 2 Finite element simulation results of components under different parameters

由式(10)计算所得墙体抗剪承载力结果与有限元模拟结果对比如表3所示，由表3可以看出，计算值与模拟值误差在5%左右，最大误差为6.14%，说明二者吻合程度较高。

3.2 钢板仓组合剪力墙抗剪承载力计算公式修正

由钢板仓组合剪力墙的抗剪承载力计算与模拟结果对比分析可以看出，计算公式吻合度较高，但有一些数据误差较大，且数据量少。故采用均匀设计试验法，丰富墙体的结构形式，增加数据量，并对数据通过数理统计的方法加以修正，提高公式的可靠性。

3.2.1 均匀试验设计

在实际结构设计中，墙体的组成千变万化，单参数分析只能得到各项参数对墙体承载能力的影响。为尽可能全面考虑墙体的结构形式，以尽可能少的计算量反映更全面的结构组成情况，采用均匀设计试验法[10]，对多组参数进行组合分析，均匀取点，建立相应模型进行低周往复加载，提取相应数据。

选取参数分析的6个因素，分别为：剪跨比、钢板强度等级、钢板厚度、轴压比、墙体厚度和混凝土强度。每个因素取5个水平进行试验设计，各因素的水平选取分别为：

X1(剪跨比)：1.5、1.75、2.0、2.25、2.5；

X2(钢板强度等级)：Q235、Q345、Q390、Q420、Q460；

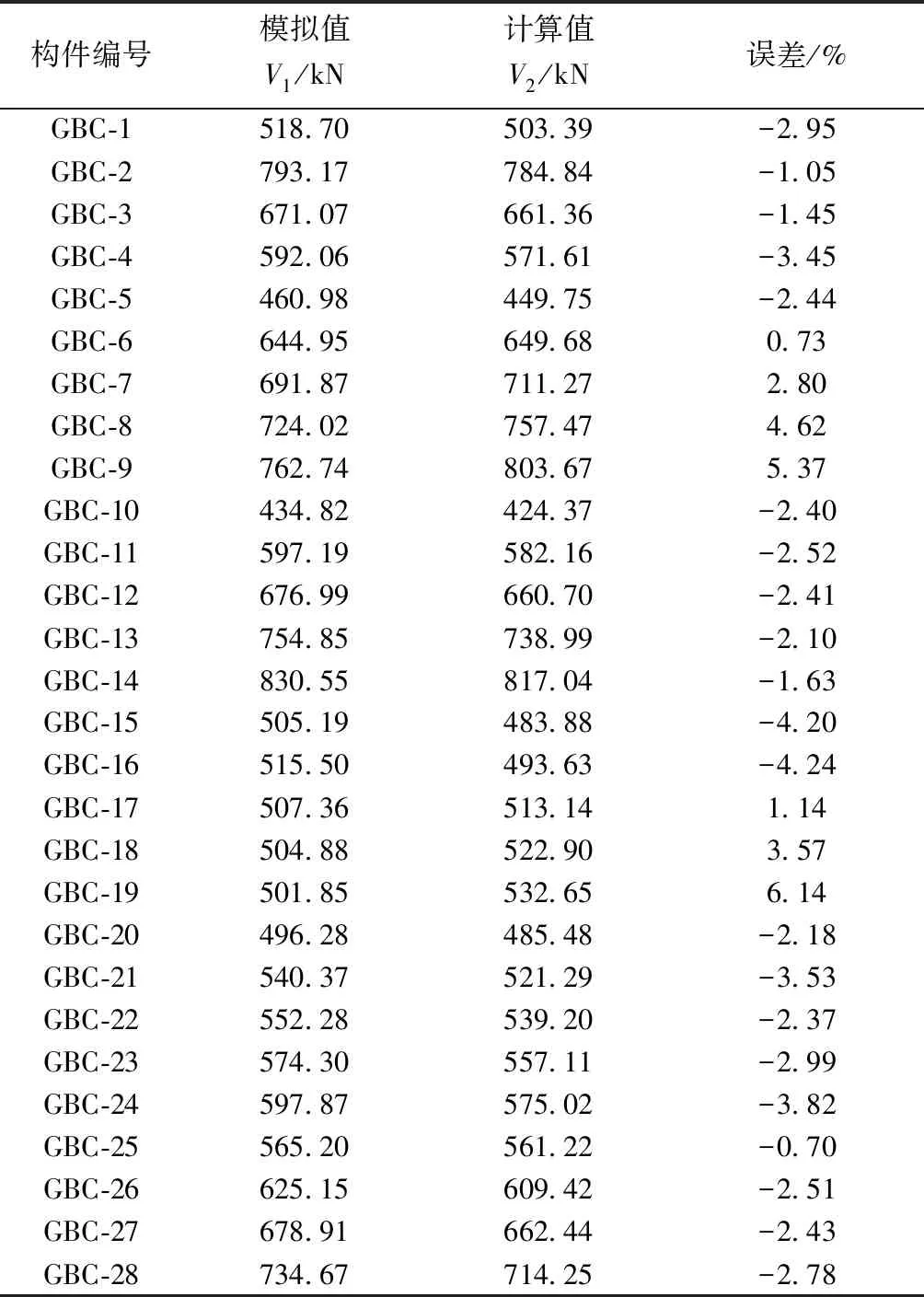
表3 抗剪承载力计算结果与模拟结果对比Table 3 Comparison of calculation results of shear capacity and simulation results

X3(钢板厚度)：3、4、5、6、7 mm；

X4(轴压比)：0.3、0.4、0.5、0.6、0.7；

X5(墙体厚度)：120、130、140、150、160 mm；

X6(混凝土强度)：C30、C40、C50、C60、C70。

选用U10(1010)来提高试验设计的精确度，保证均匀选取各因素，提高试验的可靠度。具体参数值选取如表4所示。

表4 均匀设计具体参数值Table 4 Uniform design specific parameter values

利用有限元软件ABAQUS对表4内的构件进行有限元建模，控制轴向力稳定后进行低周往复加载，得到各个构件的骨架曲线如图11所示，从图11中可以提取各个构件的峰值荷载V1。

3.2.2 数据回归分析

将表4各构件具体数据代入式(10)，可以得到钢板仓组合剪力墙抗剪承载力计算值V2，与模拟值V1进行对比，结果如表5所示。

利用统计分析软件SPSS对表3与表5的数据进行线性回归分析，其相关系数r=0.997。同时，数据的方差分析以及系数结果如表6、表7所示，标准化残差直方图及残差正态概率图如图12所示。

由上述分析可知，计算结果具有95%的保证率，且钢板仓组合剪力墙抗剪承载力计算结果的修正公式为

V=1.005V2+0.752

(11)

式(11)中：V为修正后的钢板仓组合剪力墙抗剪承载力计算结果；V2为钢板仓组合剪力墙抗剪承载力计算结果。

表6 方差分析表Table 6 Analysis of variance

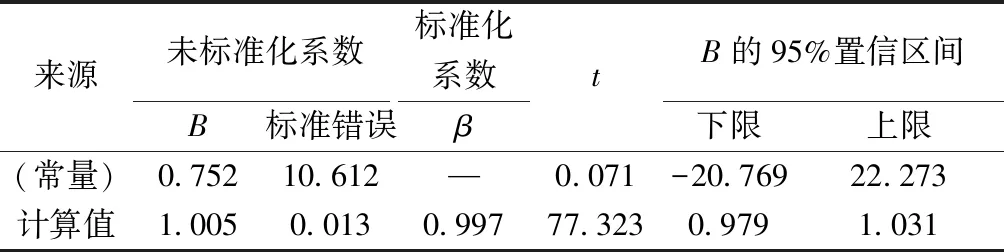
表7 回归系数与置信区间Table 7 Regression coefficients and confidence intervals

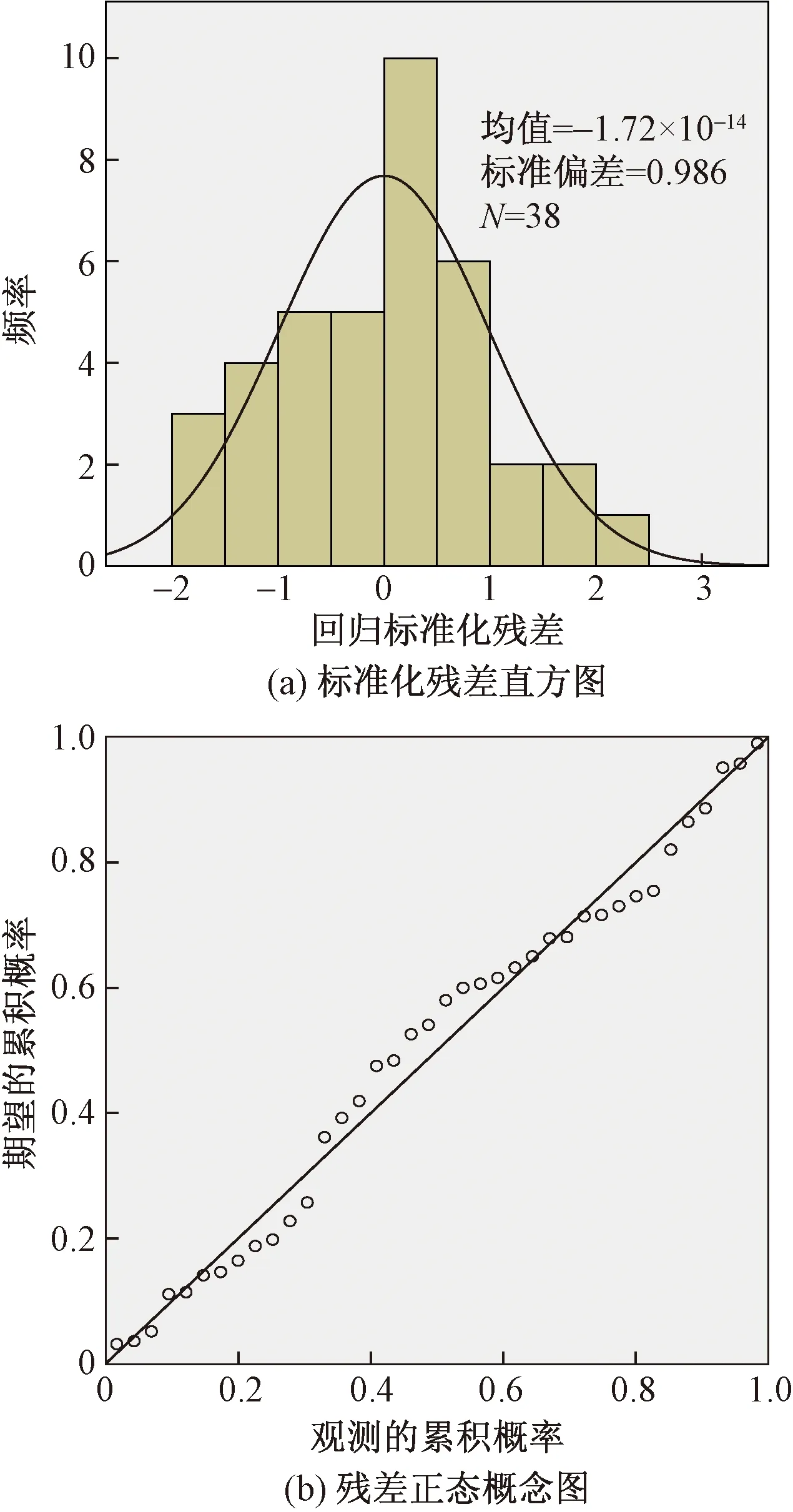
图12 标准化残差直方图及残差正态概率图Fig.12 Normalized residual histogram and residual normal probability plot

4 结论

(1)钢板仓组合剪力墙的承载能力随剪跨比的增加而降低，随钢板强度、钢板厚度、混凝土强度、墙体厚度的增加而提高。此外，当轴压比小于0.4时，承载力随轴压比的增加而提高；当轴压比大于0.4时，承载力随轴压比的增加而降低。

(2)钢板仓组合剪力墙的极限位移随剪跨比、钢板强度、钢板厚度增加而增大，随轴压比、混凝土强度、墙体厚度的增加而减小；屈服位移随剪跨比、钢板强度、混凝土强度的增加而增大，随钢板厚度、轴压比、墙体厚度的增加而减小。

(3)钢板仓组合剪力墙的初始刚度随剪跨比、钢板强度、轴压比的增加而减小，随钢板厚度、混凝土强度、墙体厚度的增加而增大；延性系数和变形能力随剪跨比、钢板强度、轴压比、混凝土强度的增加而减小，随混凝土强度的增加而增大，随钢板厚度的增加先增大后减小，且厚度为5 mm时，变形能力更大。

(4)根据叠加法建立钢板仓组合剪力墙抗剪承载力计算公式，并利用参数分析数据和均匀试验设计数据结合回归分析对公式进行修正，结果表明公式具有95%的保证率。