改进的NSGA-Ⅱ算法的柔性物料搬运策略
2021-02-25刘晓婷刘清涛
潘 野,刘晓婷,刘清涛,武 凯
(长安大学道路施工技术与装备教育部重点实验室,西安 710064)
物料配送作为制造装配车间中重要的辅助环节,在运作成本中占据很大比例[1-2]。据相关资料显示,在制造过程中只有5%的时间用于加工装配,而95%的时间用于物料配送和存储[3],因此如何优化制造装配过程中物料的仓储和配送策略,使各种生产指标达到更优,是目前各企业提高竞争力的主要途径之一,也是制造系统研究的热点领域。Van等[4]提出了一种连续存储策略,此种策略具有较小的存储空间需求和较短的预期运输时间;Hausman等[5]在物料信息已知的情况下提出了一种定位存储策略;Gu等[6]在物料信息未知的情况下提到采用最长空闲储位策略。而对于物料配送策略,Dang等[1]以最小化机器人总运行时间为目标,对单个机器人的物料配送顺序进行决策;Nielsen等[7]研究了配送能力约束下的单机器人调度问题,并采用改进的遗传算法求解机器人每次的配送量;葛茂根等[8]提出以物料运输成本、物料运输时间和线旁库存为优化目标的多目标准时物料配送模型,并设计了混合粒子群算法来求解此模型;周炳海等[9]以降低物料的线边库存成本为目标进行了数学规划建模与分析,并提出了求解该模型的反向动态规划算法和改进蜂群算法。
已有不少文献分别对物料仓储和物料配送问题进行了研究,但大多数文献均将二者作为单独问题考虑,而没有从整体上对仓储和配送进行集成优化,从而导致系统的整体效率低、配送成本高等问题。为此,现提出以搬运机器人为中心的物料仓储策略,将整个仓库划分为多个“物料库”,某一个或几个搬运机器人需要运送的物料存放在一个“物料库”内,形成了搬运机器人与“物料库”相对应的物料存储模式;建立了考虑时间、负载和能耗的多目标多机器人协作的柔性物料配送调度模型,并提出了一种改进的非支配排序遗传(non-dominated sorting genetic algorithm-II,NSGA-Ⅱ)算法。
1 以搬运机器人为中心的柔性物料配送策略
目前最主要的物料配送方式是拉动式配送,其主要缺点是配送过程中拣货效率低、准确度低和配送成本高[10-11]。以搬运机器人为中心的存储模式是面向搬运机器人的主动式配送策略。该策略依据搬运机器人的类型及其承载量的大小,结合车间配送部门和物料供应商的供货计划和物料清单(bill of material,BOM),制订工作站物料需求量和需求时间,并对搬运性能各异的机器人分配不同的配送任务,从而使搬运机器人在不同时段主动对工作站准时配送所需物料。
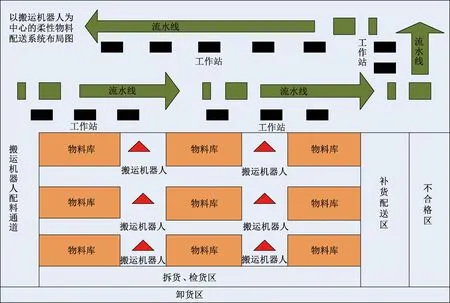
图1 以搬运机器人为中心的柔性物料配送系统布局图Fig.1 Layout diagram of flexible material distribution system centered on handling robot
以搬运机器人为中心的柔性物料配送模式的关键是采用合理的存储策略,现提出的存储策略不再以物料的类别来分区,而是依据搬运机器人来划分。物料存储区被整合为多个“物料库”,一种类型的搬运机器人所要运送的不同物料存放在同一个“物料库”内,而同一个“物料库”可能存放多个不同类型搬运机器人所要运送的物料。在同一个“物料库”内,物料可以依据搬运机器人的类型或物料类别来划分为子区域存储,这种物料的存储是面向搬运机器人的,即以搬运机器人为中心的存储。
与传统物料配送模式相比,该模式下只需由“物料库”直接对搬运机器人分配物料配送任务,而搬运机器人只在与其相对应的“物料库”内拣货,大大降低了拣货过程中的搜索范围和时间,提高了配送效率;物料配送路径也基本固定,能有效避免多个机器人在整个仓库范围内协作时出现的路径冲突问题,以保证生产的循环有序进行。此种配送策略将存储物料的仓库划分为卸货区、检货区、存储区、不合格区和补货配送区,其具体位置划分如图1所示。
2 以搬运机器人为中心的柔性物料配送模型建立
2.1 问题描述
装配车间的物料配送是依据各种工件的不同工序在不同工作站的物料需求,找到合理的搬运机器人的调度和配送方案,使配送过程中的各项约束得到满足,同时使时间等目标最优,最终将物料准确及时地配送到各个工作站,具体的问题描述如下。
在一个装配车间中搬运机器人的数量为V,不同工件的数量为P,工作站的数目为N,工件在工作站所需的物料的配送顺序由工件的工序决定,不同工件在不同工作站的物料配送任务可由多种不同的搬运机器人完成,且同一任务由不同的搬运机器人完成的时间也不同。物料配送的调度目标是为每个工件在不同工作站的物料配送选择合适的搬运机器人,以及确定每台搬运机器人的所有任务的最佳配送先后顺序和起始时间,使总的配送时间、搬运机器人的总负载及搬运总能耗等目标达到最优。现针对该配送调度任务做出如下假设。
(1)搬运机器人的启动时间、停止时间和运行故障等问题忽略不计。
(2)配送任务一旦开始不能中断。
(3)搬运机器人均由仓储配送中心的“物料库”出发,将物料运送至工作站,再返回至原位置,此次配送任务结束。
(4)工件在工作站所需物料的装载和卸下时间均属配送时间内。
(5)每个工件在前一个工作站所需物料配送完成以后才能开始该工件在下一个工作站所需物料的配送。
(6)同一搬运机器人前一个配送任务完成以后才能开始下一个配送任务。
2.2 变量描述
物料配送调度模型所涉及的变量如下:
i:搬运机器人的编号,i=1,2,…,V;j:工件的编号,j=1,2,…,P;k,s,l:工作站的编号,k,s,l=1,2,…,N;Ti:编号为i的搬运机器人完成所有物料配送任务的最后配送完成时间;Tj:编号为j的工件在工作站所需物料全部配送完成时间;Tp(j):编号为j的工件在工作站所需物料全部配送完成的规定期限;Tijk:搬运机器人i完成工件j在工作站k所需物料配送任务的时间;P′0:装配车间的固有能耗的平均功率;Pi:搬运机器人i工作过程中能耗的平均功率;P′i:搬运机器人i闲置过程中能耗的平均功率;Xijk=1,表示搬运机器人i对工件j在工作站k所需物料进行配送,否则Xijk=0。
2.3 物料配送调度模型建立
以搬运机器人为中心的柔性物料配送调度模型是以总配送时间最短、总延期时间最短、搬运机器人的总负载最小和搬运总能耗最小为目标的多目标优化。多目标优化的调度模型相比于单目标可以使系统的性能水平达到更优。根据2.1节中的问题描述和假设,物料配送调度模型的目标函数如下:
(1)
(2)
(3)

(4)
式中:f1为使搬运机器人完成所有工件在工作站所需物料配送的时间最短;f2为使搬运机器人完成所有配送任务的总延期时间最小;f3为使搬运机器人完成所有配送任务的总负载最小;f4为使搬运机器人完成所有配送任务的总能耗最小。
目标函数f1、f2、f3和f4需要满足的约束条件为
Qmjk-Tmjk≥Qij(k-1)
(5)
Qigs-Tigs≥Qijl
(6)
Tj≤Tp(j)
(7)
在约束条件中,式(5)为工件j在工作站k所需的物料必须在工作站k-1所需物料配送完成之后才能开始配送,其中Xmjk=Xij(k-1)=1,1≤j≤P,1≤m≤V,1≤k≤N;式(6)为任一确定的时间点,搬运机器人i既不能为不同工件配送物料,也不能为不同工作站配送物料,即同一搬运机器人上一个配送任务完成以后才能开始下一个配送任务,其中Xigs=Xijl=1,1≤i≤V,1≤g≤P,1≤s,l≤N;式(7)为工件j在工作站所需物料全部配送完成的时间不能超过规定期限,其中1≤j≤P。
3 改进的NSGA-Ⅱ算法
3.1 算法主流程
改进的NSGA-Ⅱ算法的主要流程如图2所示。首先,随机生成一个规模为N的初始种群P0;接着对P0进行快速非支配排序和拥挤度计算,通过二元锦标赛选择适合繁殖的父代种群,再对父代种群进行自适应交叉和变异得到子代种群Q0,令t=0;然后得到新的种群Rt=Pt∪Qt,对Rt重复上述的Pareto排序分级、拥挤度计算、选择、交叉和变异操作得到新的种群Pt+1;再对种群Pt+1重复上述一系列操作直至满足进化代数的要求;最后,对进化完成的最后一代个体进行非支配排序和拥挤度计算,得出最优解。
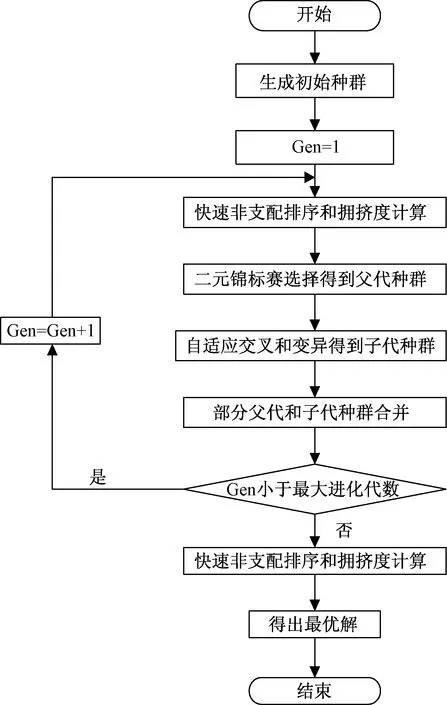
图2 改进的NSGA-Ⅱ算法流程图Fig.2 Improved NSGA-Ⅱ algorithm flowchart
3.2 染色体的编码设计
对于遗传类的算法来说染色体的编码尤为关键,编码方法是否合理对最优解的质量和算法的运行效率有直接影响,较好的编码方法可以提高算法的收敛速度,在较短的时间内快速得到最优解[12]。所设计的方法是基于工件和搬运机器人的编码,将工件、工作站、搬运机器人以及时间全部信息编入一个结构体J中,第一染色体为“工件-工作站”编码,第二染色体为搬运机器人编码,第三染色体为搬运机器人在结构体J中的位置索引编码,三个染色体上的基因严格遵循“(工件-工作站)-搬运机器人-位置索引”一一对应的关系,通过位置索引的编码信息可以快速找到某个工件在某个工作站需要的物料由某个搬运机器人配送的时间信息,例如染色体第一个位置“1-2-1”表示第1个工件在第1个工作站需要的物料由2号搬运机器人配送。其中第一和第二染色体上的基因为显性基因,可参与交叉和变异操作,第三染色体上的基因为隐性基因,不参与交叉和变异,只随着第一和第二染色体上的显性基因变化而变化。假设有3个工件,4个工作站,8个搬运机器人,对其进行三染色体编码的方式如图3所示。
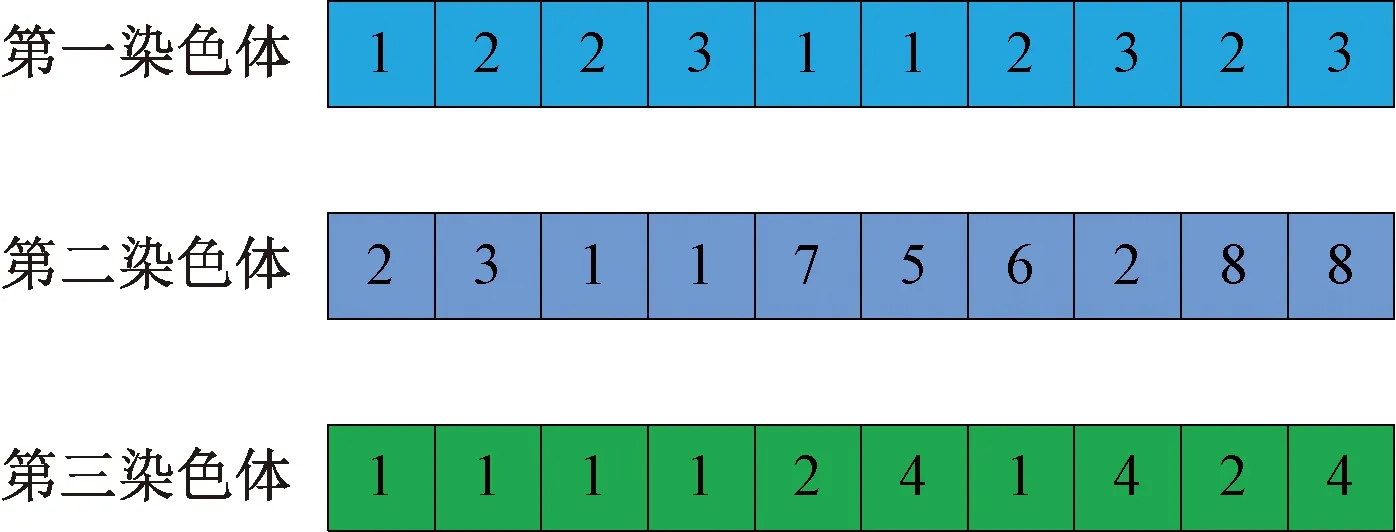
图3 三染色体编码方案Fig.3 Trichromosome coding scheme
3.3 快速非支配排序算子
在NSGA-Ⅱ算法中,快速非支配排序的目的是将初始化种群中的所有个体依据支配关系进行Pareto排序等级的划分,Pareto排序等级反映了种群中个体的优劣程度[13]。设计的快速非支配排序算子中,不同个体通过比较目标函数占优比例来确定其优劣,具体流程设计如下:
Step1对于初始化种群S中所有个体执行如下操作。
(1)令ESi=Φ,用来放置个体i所支配的个体的集合;令DSi=0,用来记录支配个体i的个体数量。
(2)判断种群中个体i和j的支配关系。
①分别计算个体i和j的目标函数fi1、fi2、fi3、fi4和fj1、fj2、fj3、fj4的值。
②初始化计数变量D0=0、D1=0和D2=0,比较fi1与fj1、fi2与fj2、fi3与fj3、fi4与fj4的值,若fi1=fj1,则D0=D0+1,若fi1
③若D2=0且D0≠4,则个体i支配个体j,ESi=ESi∪j,若D1=0且D0≠4,则个体j支配个体i,DSi=DSi+1。
④若DSi=0,证明种群中没有个体支配个体i,则iRank=1,将个体i加入Rank=1的集合F1中,即F1=F1∪i。
Step2执行Step1,直至筛选出种群中Rank=1的所有个体。
Step3初始化Pareto排序等级计数器f=1,若Ff≠Φ,则:
(1)令Q=Φ,此集合用来放置Rank=f+1的个体。
(2)对当前支配解集Ff中的个体i执行如下操作:
对ESi中的每个个体j(j≠i)执行以下操作:
①令DSj=DSj-1。
②若DSj=0,则证明在种群中除去Rank=1所剩下的所有个体不存在支配个体j的,因此jRank=f+1,将j放入集合Q中,即Q=Q∪j。
(3)此时集合Q中放置的就是Rank=2的个体,因此Ff=Q。
(4)令Pareto排序等级计数器f=f+1。
Step4重复执行Step3直至种群S中所有个体Pareto排序等级全部划分完成。
3.4 拥挤度计算和比较算子
在NSGA-Ⅱ算法中,拥挤度是指种群中给定个体的周围个体的密集程度,拥挤度和Pareto排序等级一样都可以为后续算法中的选择操作提供判断依据,从而选择出优秀的父代进行进化,保证了种群的多样性[14-15]。个体拥挤度计算步骤如下:
Step1初始化变量计数器k=1,对种群S中所有个体i的目标函数值fk(1≤k≤4)进行升序排列。
Step2筛选出所有个体i的fk的最小值fkmin和最大值fkmax。
Step3计算种群S中所有个体i的ikd,将第一个和最后一个个体的ikd设为无穷大,剩余个体的ikd的计算为
(8)
Step4令k=k+1。
Step5重复上述Step1~Step4直至种群S中所有个体i的ikd计算完毕,则种群S中所有个体i的拥挤度id的计算为
(9)
在拥挤度比较算子中,对于种群S中的任意两个个体i和j,两者比较的关键在i和j的Pareto排序等级和拥挤度,具体的比较步骤如下:
Step1对于种群S中的任意两个体i和j,其Pareto排序等级为iRank和jRank,拥挤度为id和jd。
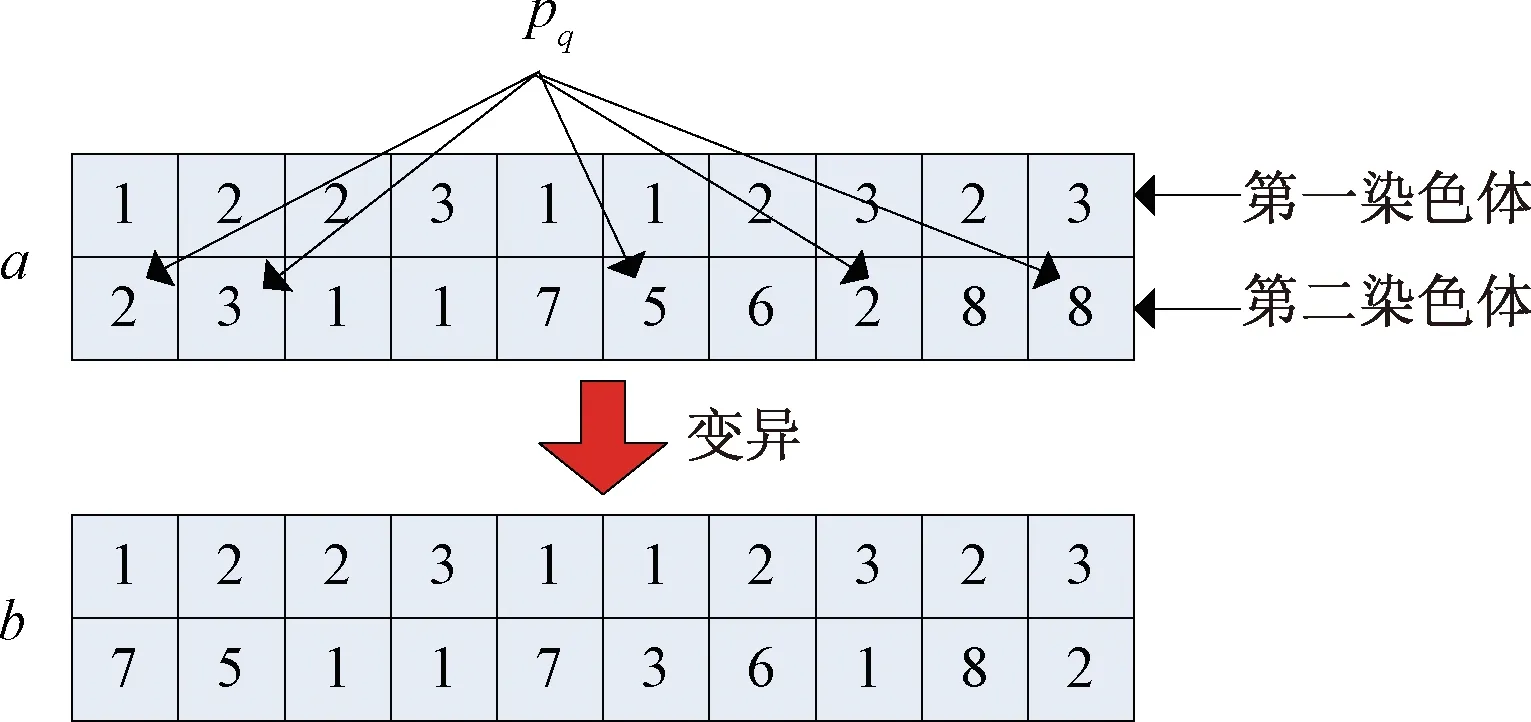
Step2若iRank 遗传算子在NSGA-Ⅱ算法中由选择算子、交叉算子和变异算子组成,遗传算子能够确保在进化的过程中保持种群的多样性和精英性,提高算法的收敛速度和避免局部最优。 3.5.1 选择算子 最常用的选择算子有比例选择算子、排序选择算子、联赛选择算子和精英选择算子等。采用的选择算子为二元锦标赛选择算子,其在NSGA-Ⅱ算法中的主要思想为:在已经完成Pareto排序等级和拥挤度计算的种群S中任选两个个体,通过调用3.4节中的拥挤度比较算子,先比较两者的Pareto排序等级,若不同则取Pareto排序等级较小的个体作为父代,若相同则再比较两者的拥挤度,选择拥挤度较大的个体作为父代,直至满足所需父代个体的数量选择操作结束。这种选择方法有利于确保种群的多样性,从而得到全局最优解。 3.5.2 交叉和变异算子 在种群的进化过程中,交叉和变异算子对算法的搜索性能起着至关重要的作用,因此本文设计了自适应交叉和变异算子,交叉和变异概率随着进化代数的变化而变化,通过自适应策略来增强算法对空间变化的适应能力和寻优能力,其具体过程如下: (1)自适应交叉算子。 交叉操作是将经过二元锦标赛选择后得到的父代个体中任选两个个体交换其某些位置的基因,从而得到子代个体,交叉操作的具体步骤如下: Step1令Pc=[0.4 0.8],其表示交叉概率,Pc,min=0.4,Pc,max=0.8。 Step2令循环计数变量k=1,设置自适应交叉概率为 (10) Step4在染色体上任取几个需要交叉的位置pl,设计的交叉方法为模拟二进制交叉,若c=mod(k,2)=1,则将个体i和j的第一染色体执行交叉操作,第二染色体和第三染色体随之变化,染色体i中非pl位置保留,pl位置与染色体j中的非pl位置对应交叉,染色体j亦是如此;若c=mod(k,2)=0,则将个体i和j的第二染色体执行交叉操作,第一染色体和第三染体随之变化,染色体i和j的pl位置对应交叉,从而得到新的个体m和n。其具体交叉过程如图4所示。 图4 染色体交叉操作Fig.4 Chromosome crossover operation Step5令k=k+1,执行变异操作,循环重复Step1~Step4直至产生的新个体数量满足所需要求即可。 (2)自适应变异算子。 变异操作是产生新个体的辅助方法,由于遗传类算法容易陷入局部最优的困境,因此在种群进化的后期需要增大变异概率来跳出局部最优。变异具体步骤如下: Step2设置自适应变异概率为 (11) Step3在[0 1]产生一个随机数r2,若满足条件r2 图5 染色体变异操作Fig.5 Chromosome mutation operation 为了验证模型和算法的有效性,以某汽车部件装配车间为例进行验证。某汽车部件装配车间的搬运机器人的数量V=8,不同工件的数量为P=8,工作站的数量为N=6,在物料配送的过程中,不同工件需要的工作站的数目是不同的,并且某一工件在某一工作站的物料配送选用不同的搬运机器人所花费的时间也是不同的,其具体的工件、搬运机器人和时间信息的集合如表1所示,例如1号工件在工作站1的物料配送可选用的搬运机器人为4、6和7,对应的耗时为14、10和11。能耗的功率信息如表2所示,例如1号搬运机器人工作过程中能耗的平均功率为20,闲置过程中能耗的平均功率为3.45。 为验证所提算法的有效性,采用经典的NSGA-Ⅱ算法和改进的NSGA-Ⅱ算法进行对比分析。在经典的NSGA-Ⅱ算法中,参数的设置分别为:初始种群的数量为Pf=100,交叉概率为Pc=0.8,变异概率为Pm=0.1,种群进化的代数为Gen=15,算法的终止条件是种群进化到给定代数之后停止进化,输出最优解;在改进的NSGA-Ⅱ算法中,参数的设置分别为:初始种群数量为Pf=50,交叉概率Pc和变异概Pm为式(10)和式(11)所表示的随着进化代数不断变化的动态自适应值,种群进化的代数为Gen=15,算法是终止条件是种群进化到给定代数之后停止进化,输出最优解。算法的编写运行和模型的求解都在软件MATLAB2016a上完成,经典的NSGA-Ⅱ算法和改进的NSGA-Ⅱ算法对上述实例的求解具体结果如表3所示。 在表3中,t(8,1)=[0,18]表示编号为i=1的搬运机器人的第一个配送任务是为j=8的工件在k=1的工作站所需的物料进行配送,配送的起始时间和终止时间为0和18。通过比较表3中的两种算法的实例求解结果可以得出:在进化代数相同的条件下,改进的NSGA-Ⅱ算法相较于经典的NSGA-Ⅱ算法,在初始种群的数量减少50%的情况下,目标函数f1、f2、f3和f4的值依然可以得到很好的优化。对于目标函数f1来说,所有物料配送任务完成的时间由99降至79,节省了大约20%的时间;对于目标函数f2来说,两种算法的配送调度方案都可以在规定期限内完成所有任务;对于目标函数f3来说,搬运机机器人的总负载由357升至365,总负载上升大约2.2%,两种算法的配送调度方案的总负载基本相同;对于目标函数f4来说,搬运机器人的搬运总能耗由122.56降至109.85,节约了大约11.2%的总能耗。因此,在以搬运机器人为中心的柔性物料配送模型的求解过程中,改进的NSGA-Ⅱ算法表现出了更好的求解性能,得到了更加合理的配送方案,同时验证了算法的可行性和有效性。 建立了一种柔性物料搬运系统模型,提出了一种改进的NSGA-Ⅱ算法。首先阐述了以搬运机器人为中心的柔性物料配送基本策略,并且设计了相应的系统布局图;接着建立了以完工时间、延期时间、负载和能耗等目标最小化的多目标多机器人协作物料配送模型,设计并改进了NSGA-Ⅱ算法的流程、编码方法和遗传算子。最后以某汽车部件装配车间为例,运用经典的NSGA-Ⅱ算法和改进的NSGA-Ⅱ算法分别对模型进行求解,验证了算法的可行性和有效性。研究表明,改进的NSGA-Ⅱ算法具有更优的求解性能,使得目标函数值可以达到更优。3.5 遗传算子

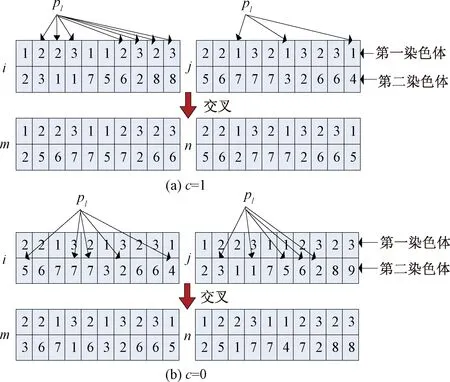

4 算例分析
5 结论
