单级跨声速压气机旋转失速模拟方法

王子维, 刘东健, 陈 逖

(中国空气动力研究与发展中心, 四川绵阳 621000)

引 言

压气机的气动稳定性是影响航空发动机性能、 稳定性、 安全性和寿命的关键因素之一. 为了避免压气机出现气动失稳, 须对其设计进行折衷, 这通常会导致压气机设计点性能的降低. 通过对压气机的气动失稳现象进行研究, 探索其流动机理, 对于找到可行的抑制失稳的流动控制方式, 从而拓宽压气机的失稳边界, 改进设计, 提高压气机设计点的性能, 有着积极的促进作用.

旋转失速是压气机气动失稳的主要表现形式之一. 目前, 旋转失速的流动机理尚未完全建立起来[1]. 当前对于旋转失速的模拟主要分为建模分析和全三维数值模拟两种. 通过对压气机的叶排效率和落后角等建模, 可以在一维尺度上完成压气机失速边界的快速预测[2]. 然而, 这种方法对于探索压气机失速流动机理并无作用. 另外, 南航屠宝锋[3], 郭晋等[4]采用三维非定常可压缩Euler方程和三维激波盘模型, 发展了一种可分析风扇/压气机三维非定常动态失速过程的计算模型和计算程序. 这种计算模型可以较准确地模拟失速前压气机内部非定常流动的变化情况, 然而并没有将黏性的影响考虑在内. 有较多的研究者对压气机进行全三维黏性定常模拟, 通过计算发散来判断压气机是否失稳[5]. 然而, 这种方法有一定的局限性, 数值发散与流动失稳并不能完全对应; 另外, 这种方法也无法模拟压气机失速前后非定常流动的变化过程. 由于压气机旋转失速是全周的、 强非定常性的流动现象, 因此通过全环非定常模拟方法模拟旋转失速的发展过程, 是相对更为准确的方法. 例如， 鞠鹏飞等[6]采用自主研发的MAP程序对单转子NASA Rotor37的失速发展过程进行了模拟, 贺象等[7]采用商业软件CFX对北航低速大尺寸单转子的失速发展过程进行了模拟, 李清鹏等[8]采用商业软件NUMECA对某亚声速轴流压气机转子的失速过程进行了模拟. 失速过程模拟的难度较大, 极易出现流量持续下降的计算发散现象, 由于多排压气机存在叶排间的转静干涉, 其失速过程的模拟难度更大. 吴艳辉等[9]采用商业软件NUMECA对某单级轴流压气机的失速过程进行了模拟. 然而, 其仅模拟了流动失稳的起始过程, 并没有模拟出失速由出现先兆到完全发展的整个过程.

因此, 为了准确复现多排压气机中失速发展的完整过程, 发展了守恒的动态重叠网格技术, 以准确传递叶排间的流动信息; 发展了流量出口边界条件, 以快速逼近失速边界; 发展了节流阀边界条件, 以准确模拟失速发展的过程.

1 多排压气机旋转失速模拟方法

1.1 守恒的动态重叠网格技术

发展了基于单元相交的守恒重叠网格方法. 以叶排交界面为对称面, 由于数值方法是2阶的, 因此在叶排交界面处将网格外推两层虚拟网格. 以相邻叶排网格单元(即贡献单元)对虚拟网格单元进行切割, 以虚拟网格单元落在各个贡献单元内的体积占虚拟网格单元体积的比例为权重系数, 对各个守恒单元的守恒变量进行加权平均, 得到虚拟网格单元内守恒变量的值.

1.1.1 网格相交法

守恒性重叠网格技术的核心为网格相交法[10-12]. 对于相交的两个网格单元Cell 1与Cell 2, 须求出这两个单元的相交体. 由于结构网格单元与非结构网格单元均可分解为1个或多个四面体单元, 则这两个单元可以表示为两组四面体单元{T11,T12,…,T1n}与{T21,T22,…,T2m}. 于是上述问题便转化为求这两组四面体单元的相交体.

如图1所示, 四面体P1属于第1个网格单元, 四面体P2属于第2个网格单元. 通过Sutherland-Hodgman 算法便可求出两个四面体单元相交得到的多面体P3.

图1 四面体相交示意图Fig. 1 Tetrahedron intersection

将两组四面体单元两两求交, 得到多个相交体{I1,I2…,Imn}, 然后取并集, 便可以得到两个网格单元的相交体I. 已知{I1,I2…,Imn}中每个体积和体心坐标, 可以求出I的体积和体心坐标: {I1,I2…,Imn}的体积之和为I的体积; 以{I1,I2…,Imn}中每个单元的体积除以I的体积作为权重系数, 对这些单元的体心坐标进行加权平均, 可以求出I的体心坐标.

通过上述步骤可以求出Cell 1与Cell 2的相交体I的体积和体心坐标. 不失一般性, 假设Cell 1为贡献单元, Cell 2为插值单元. Cell 1的格心值为q1, 则加权后Cell 1的格心值对Cell 2的格心值贡献为q1VI/VCell 2. 其中,VI为I的体积,VCell 2为Cell 2的体积.

1.1.2 快速的并行动态重叠网格技术

与主流做法相同, 基于MPI实现并行的动态重叠网格计算. 考虑到压气机几何与运动规律的特殊性, 故提出两个技术, 用于提高并行动态重叠计算的效率.

第1个技术细节如下： 收集紧邻同一个叶排交界面的网格块, 将这些网格块所属的进程收集起来, 单独建立通信子； 同时在分区时, 尽量将不同交界面处的网格块放在不一样的进程里. 通过这种方式, 在大规模模拟中, 基本可以做到每一个交界面处的网格块所属的进程组与其他交界面处网格块所属的进程组交集为空， 大大简化了编程工作. 基于分治的思想， 将大的进程分组拆分成一个个小的进程组， 每个小的进程分组处理其对应的交界面处的动态重叠计算， 相比在大的进程分组里直接处理所有交界处的动态重叠计算， 极大地降低了进程空等情况出现的频率, 提高了并行计算效率.

第2个技术的细节如下： 由于压气机固有的时间上的周期性特征, 其插值关系是周期性出现的, 存储一个周期的插值关系便可以避免重复地进行找点和插值关系计算. 考虑到压气机叶排交界面运动方式为确定的旋转运动, 基于这个特征可以对一个周期内插值关系的建立进行进一步的优化, 在前一步插值关系的基础上进行较少的计算得到下一步的插值关系.

1.2 失速边界逼近技术

在大流量工况下, 设置压力出口边界条件, 即设定出口机匣壁面处静压, 并采用径向平衡方程得到出口静压分布. 然后通过逐步提高出口反压的方式逐步推进到压气机近失速点. 以近失速点的流场为初场, 进行压气机稳定边界附近的流动模拟. 在压气机稳定边界附近, 考虑到出口反压较高时, 若依然固定机匣处为静压, 有可能得到不符合物理实际的流场解. 为避免出现这种情况, 设计流量出口边界. 通过二分法的形式逐步调低流量, 以最大限度逼近失速边界.

以NASA Stage 35为研究对象[13], 其数模如图2所示, 其设计参数如表1所示.

生成全环结构化网格, 所有物面第1层网格的厚度保证y+=1, 网格块数量为728, 网格单元数为2.2×107, 转子网格与静子网格之间通过滑移网格面交换数据, NASA Stage 35的物面网格见图3.

图2 NASA Stage 35数模Fig. 2 Numerical model of NASA Stage 35

表1 NASA Stage 35的设计参数Table 1 Design parameters of NASA Stage 35

图3 物面网格Fig. 3 Grids of wall surface

基于自主研发的轴流压气机数值模拟软件ASPAC对NASA Stage 35进行了堵塞状态到失速边界状态的模拟. ASPAC采用有限体积法求解Reynolds时均N-S方程, 对流通量采用Roe格式计算, 黏性通量采用中心差分方法计算, 湍流模型为SA模型. 软件基于MPI实现了并行计算能力. 对于非定常模拟, 采用Jameson的双时间步方法. ASPAC在叶轮机械的数值模拟上经由多个标模进行了计算验证, 计算结果与实验结果吻合较好, 计算精度与商业软件的计算精度相当[14]. 在全环非定常模拟中, 在压气机转一圈的时间内采用2 000个物理时间步, 子迭代步数为50. 模拟结果与NASA数值模拟程序TURBO[15]和实验结果的对比如图4所示. 其中, 实线为3种结果对应的压比, 绿色虚线与蓝色虚线分别表示ASPAC和TURBO计算结果与实验值的误差, 计算公式如下

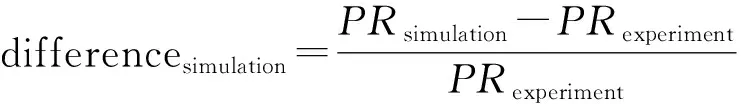
其中, 某一流量下对应的压比通过线性插值得到.

图4 模拟与实验结果对比Fig. 4 Comparisons between simulation and experiment

ASPAC和TURBO的计算结果与实验结果的误差如表2所示, 基于实验值计算了相对误差. 在堵点附近, 两个软件的模拟结果与实验结果的误差均较大, 这是由于堵点附近流量-压比曲线的斜率绝对值极大, 较少的扰动便会导致很大的误差; 随着流动向近失速点靠近, 两个软件的模拟结果与实验结果的误差很快缩小.

表2 数值模拟结果与实验结果误差Table 2 Differences between simulation and experiment

1.3 节流阀边界条件

以近失速状态的非定常流场为初场, 进行全环非定常续算. 通过添加节流阀边界条件, 模拟了失速由起始到完全发展的全过程. 节流阀边界条件为

2 模拟结果

在失速模拟的计算初期, 固定机匣处静压以排除人为扰动的可能, 在流量稳定以后, 根据稳定状态下的流量和出口压力, 确定节流阀开度系数, 并将出口边界条件改为节流阀边界条件. 在失速模拟的整个过程中, 节流阀开度系数保持不变.

失速发展整个过程的流量变化如图5所示. 在添加节流阀边界条件后, 流量在开始几圈保持稳定状态, 在第10圈的时候, 随着失速扰动的出现, 流量急速下降, 约0.5圈后降到了最低点. 流量在最低点维持到第14圈, 并花费了约3圈的时间进入到稳定失速状态. 流量剧烈变化的细节方法如图6所示.

图5 失速发展过程的入口流量变化Fig. 5 Variation of inlet mass flow during stall development

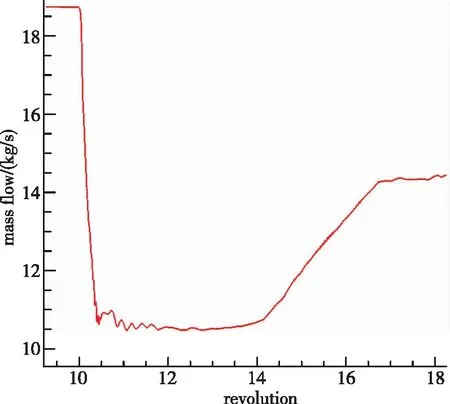
图6 失速发展过程的入口流量变化(细节图)Fig. 6 Variation of inlet mass flow during stall development(details)

压气机由稳定运行到失速完全发展过程的流量-出口静压特性如图7所示, 流量-总压比特性如图8所示. 由图7左边一段的曲线可以明显地看到出口静压与流量二次方之间的正比关系, 这与节流阀的特性相匹配.

图7 失速发展过程的流量-出口静压特性图Fig. 7 Variation of mass flow-outlet static pressure during stall development

图8 失速发展过程的流量-总压比特性图Fig. 8 Variation of mass flow-total pressure ratio during stall development

然而, 由图8可以发现, 在失速发展过程中, 流量与总压比的关系要复杂得多. 由于入口总压指定为一个大气压, 在模拟过程中保持不变, 则总压比的变化实际上正比于出口总压的变化. 图8箭头所指的近失速状态处, 在数值上减小出口节流阀开度, 导致压比快速升高, 流量快速下降, 这个扰动最终导致了旋转失速的产生. 可以看到, 在失速扰动出现以后, 随着流量的下降, 出口总压也随之下降; 在流量由最低点逐步增大并逼近失速完全状态的过程中, 出口总压随之上升, 但始终低于流量下行过程中对应的出口总压. 最终流动稳定在图8中箭头所指的旋转失速完全发展所在的位置, 旋转失速完全发展后的总压比和流量均小于近失速点的总压比和流量.

面向压气机入口, 沿着逆时针方向, 在每个转子叶片通道的机匣处依次设置数值探针, 每个通道的探针与叶片的相对位置均相同. 图9展示了失速发展过程中机匣处探针上的静压随时间的变化. 图9对静压进行了归一化处理, 展示了1, 4, 7, 10, …, 34号转子叶片通道的静压随时间的变化. 可以看到, 失速扰动起始伴随着机匣静压的跃升, 且不同叶片通道的机匣处静压跃升几乎是同步的. 经过大约7圈的时间, 扰动逐步增大, 并在最后发展成稳定的失速团. 失速团转速与压气机转速方向相同, 约为压气机转速的46.41%.

图9 不同叶片通道机匣处的静压变化Fig. 9 Variation of static pressure on the shroud in different blade passages

失速先兆阶段与完全失速时, 压气机s1流面(95%叶高)的相对Mach数分布及流线如图10所示. 如图10(a)所示, 由于节流阀开度减小, 流动出现了堵塞, 堵塞的现象发生在所有叶片通道. 如图10(b)与(c)所示, 在失速完全发展阶段, 出现了一大一小两个失速团. 沿着转子转动方向, 在失速团正方向的叶片, 来流冲角减小, 将会解除该叶片周围的流动分离; 在失速团反方向的叶片, 来流冲角增大, 将会导致该叶片出现流动分离; 这两个效应结合, 导致了失速团沿着叶片转动反方向传播.

(a) Stall inception

由于硬盘存储空间的限制, 没有存储从流动堵塞阶段到失速团完全发展阶段每一步的流场, 无法详细分析从流动堵塞阶段到失速完全发展时压气机内部流动的演化细节. 然而, 从失速发展过程的流量变化情况, 以及机匣处采样点的静压变化情况, 可以分析得知, 在通过关紧节流阀施加扰动之后, 流量减小, 机匣处静压升高, 随着流动的部分恢复, 最终形成了两个典型的失速团.

压气机由稳定运行到失速完全发展前, 失速发展中和失速完全发展时, 轴向Mach数等值面分别如图11～13所示.

图11 转动到第4.5圈时的轴向Mach数等值面(Ma=-0.1, 静压着色)Fig. 11 Iso-surface of axial Mach number at 4.5th revolution(Ma=-0.1, colored by static pressure)

图12 转动到第12.65圈时的轴向Mach数等值面(Ma=-0.1, 静压着色)Fig. 12 Iso-surface of axial Mach number at 12.65th revolution(Ma=-0.1, colored by static pressure)

图13 转动到第26.7圈时的轴向Mach数等值面(Ma=-0.1, 静压着色)Fig. 13 Iso-surface of axial Mach number at 26.7th revolution(Ma=-0.1, colored by static pressure)

由于展示的是Ma=-0.1的等值面, 可以认为该等值面在一定程度上代表了逆流区的位置和大小. 可以看到, 逆流区逐步由转子的吸力面蔓延到压力面; 同时, 逆流区逐渐由轴对称变为非轴对称. 由图13可以看到, 当旋转失速完全发展后, 转子区域出现一大一小两个失速团; 同时, 在静子的压力面也出现了逆流区, 且与转子区域的失速团相邻. 最后, 在旋转失速发展的整个过程中, 逆流区主要存在于压气机的叶尖区域.

压气机失速完全发展后, 95%叶高的熵分布如图14所示, 高熵区域为失速团, 可以清晰地看到一大一小两个失速团， 这两个失速团的结构几乎不随时间变化.

图14 转动到第26.7圈时95%叶高的熵分布Fig. 14 Distribution of entropy at 95% span at 26.7th revolution

3 结论

ASPAC和TURBO的模拟结果与实验结果吻合较好. 尖峰型扰动几乎同时发生在不同的转子叶片通道上. 然后, 扰动逐渐增大, 最终形成的旋转失速团转速为压气机转速的46.41%, 同时失速区的流动结构几乎不随时间变化. 在尖峰型扰动后, 逆流从转子吸力面蔓延到转子压力面, 同时也影响到了静子. 在整个过程中, 逆流主要存在于叶尖附近.