基于访问树的策略隐藏文件层次属性加密方案
2021-02-25许盛伟郭春锐任雄鹏
许盛伟 郭春锐 袁 峰 任雄鹏 杨 森
1(北京电子科技学院 北京 100070)2(西安电子科技学院通信工程学院 陕西 西安 710071)
0 引 言
近年来,随着云计算的流行,大量计算以及存储从物理本机被挪至云端[1],为用户节约了大量的存储空间,受到了广大用户的喜爱。但是将数据存储在云服务器上,并不是特别安全,可能会由于云提供商搜集用户存储的消息,导致重要信息的泄露。怎样解决云存储中数据的安全问题,已经成为人们急需解决的重要问题之一[2]。近年来,基于属性加密方案的出现不仅解决了云中所存数据的安全问题,同时也实现了用户的细粒度授权,因此受到了越来越多的关注。
Sahai等[3]最先提出了基于属性的加密方案(Attributed-Based Encryption,ABE)。在该方案中,数据属主通过设定访问策略,根据属性完成加密,在解密过程中,不用获得数据访问者的具体身份信息,只用关注解密者的属性是否满足加密者设定的加密策略。Goyal等[4]又将ABE划分为两种加密方案,一种是基于密文策略,简称CP-ABE,另一种是基于密钥策略,简称KP-ABE[5]。最早提出的CP-ABE加密体制中,访问结构直接以明文形式存在,从而导致重要信息暴露。Nishide等[6]提出了一种加密方案,可以实现数据属主将数据加密的同时,也完成了策略隐藏,防止了敏感信息的泄露。近年来,文献[7-8]又结合已有方案提出了新的方案,解决了隐藏策略过程中遇到的问题。
在大多数CP-ABE加密体制中,密钥只是由单一的可信的权威机构生成,这种做法不仅非常不安全,同时也不能实现用户的跨域访问,一旦权威机构被攻破,敌手获得密钥后,就可以从密文中获得明文数据。Chase[9]提出了一种ABE加密方案,将单个权威机构变为多个授权机构,很好地解决了上述问题。Waters[10]提出了一种分布式的CP-ABE加密方案,首次通过LSSS矩阵完成了ABE加密。后续文献[11-12]提出了分布式的属性基加密方案,其优点是密文为定长的。文献[13]在多机构授权的基础上,将策略进行了隐藏。
在现有的针对云文件属性加密的方案中,针对多个层次结构文件的研究还不是特别深入,但是也有学者们提出了一些方案[14-18],但是加解密效率不是特别理想。文献[19]提出了一种多级层次结构的CP-ABE方案。该方案通过使用分层的访问结构模型解决多层次文件共享的难题,但是其将树形的访问结构以明文的形式发送给用户,容易造成一些敏感信息的泄露。
本文针对具有多级层次结构特点的文件,提出一种采用分层级的树形结构且策略隐藏的属性加密方案,同时在本方案中有多个授权机构共同工作。采用分层级的树形结构可以减少加密成本,同时访问策略的隐藏防止了敏感信息的泄露。文中用户密钥是由中央授权机构和多个属性授权机构共同生成,防止了单个授权机构被攻击导致密钥泄露的难题。
1 预备知识
1.1 双线性映射
设G和GT分别是阶为素数p,生成元为g的乘法循环群,其双线性映射e:G×G→GT,e满足以下性质:
(1) 双线性。对∀μ,ν∈G,a,b∈Zp,都有e(μa,νb)=e(μ,ν)ab。
(2) 非退化性。存在μ,ν∈G,使得e(μ,ν)≠1。
(3) 可计算性。对所有μ,ν∈G,存在有效计算e(μ,ν)≠1。
1.2 复杂性假设DBDH
设群G、GT为乘法群,阶为p,生成元为g∈G,随机整数a,b,c∈Zp,并将四元组g,ga,gb,gc∈G和随机数T∈GT发送给敌手A,由敌手A判定T是否等于e(g,g)abc。当T=e(g,g)abc时,A输出1;否则输出0。
定义敌手判断出上述问题的优势是:
AdvDBDH=Pr[A(g,ga,gb,gc,e(g,g)abc)=1]-
Pr[A(g,ga,gb,gc,T)=1]
式中:Pr表示概率或者优势。
如果没有时间多项式算法通过不能忽略AdvDBDH打破DBDH假设,则该假设成立。
1.3 具有层次结构的访问树
假设用T表示具有分层结构的访问树,在T中,具有k个访问层次,树中的节点用(x,y)表示,其中:x表示节点在树中的行位置(从上而下);y表示节点在树中的列位置(从左到右)。R(x,y)表示根节点,att(x,y)表示叶子节点。
图1为具有2个层次结构的访问树,树中圆圈表示阈值门限,如“OR”“AND”“n-of-m(n 图1 具有2个层次结构的访问树 针对访问树,有如下定义: (xi,yi):表示访问树中的级节点,最高节点为根节点R(x1,y1),其余的依次递减。parent(x,y):表示节点(x,y)的父节点。child(x,y):表示节点(x,y)的子节点。att(x,y):表示与叶子节点相关联的属性。index(x,y):表示返回一个与节点(x,y)相关联的唯一值。 在本方案中,主体包括5部分,分别为中央授权机构(Central Authority,CA)、属性授权机构(Attribute Authority,AA)、数据属主 (Data Owner,DO)、用户(User)和云服务提供商(Cloud Service Provider,CSP)[7]。 各主体的主要功能如下: 1) CA为可信机构,通过输入安全参数,产生主公钥和主私钥,同时为AA和User生成身份标签,当用户注册完成后,为User生成密钥组件。 2) AA根据User属性生成部分密钥组件。 3) DO在本地加密需要共享的文件,由于直接采用CP-ABE加密文件,会花费比较长的时间,因此在本文中,DO首先通过AES或SM4算法生成文件密文,再采用CP-ABE算法加密文件密钥,最终把完整的密文上传至云端。 4) User 用户从云服务端下载完密文数据,当用户属性满足数据属主定义的属性时获得属性加密的密钥,再解密文件数据。 5) CSP是“诚实但好奇”的文件存储机构,能够为用户提供足够的文件存储空间,然而,为了获取利益,还是会尽可能多地收集所存储的数据信息。 在本方案中,由敌手Adversary和挑战者Challenger二者通过交互式的游戏,构建敌手挑战模型[20],具体描述如下: 1) 初始化操作(Initialization)。Adversary将选择的访问结构W发送给Challenger。 2) 系统建立(Setup)。Challenger在游戏过程中通过方案中的初始化算法得到系统公钥和密钥主私钥,主私钥由Challenger保存,将公钥发送给Adversary。 3) 查询阶段1(QueryPhase1)。Adversary选择属性Si,Si∉W,并重复从Challenger处获得私钥SK,同时Challenger通过运行KeyGen生成私钥SK。 4) 挑战阶段(Challenge)。Adversary选择两条等长的消息M0和M1,Challenger通过访问结构W加密消息Mη,其中η∈{0,1},再将密文CT发送给Adversary。 5) 查询阶段2(QueryPhase2)。重复查询阶段1。 (1) CA初始化。CA输入安全参数1λ,生成群G,由第1节可知,g为其生成元,CA随机选择α,β∈Zp,计算Y=e(g,g)α和h=gβ,并根据相应的签名方案,生成签名密钥Signkey和验证密钥Verifykey。 公钥GPK=(p,g,G,GT,e,Y,h,Verifykey) (1) 主私钥GSK=(β,gα) (2) (2) 用户注册。User首先向CA发出申请,完成注册。然后CA为每个User生成全局标识符GID。在本方案中,用户不能是长期合法的,必须要有一定的期限限制,因此CA必须为User设定有效期限Tpov。最后,为了能够辨别User身份的真伪,生成标签Usign。Usign=(GID‖L‖Tpov,Signkey),其中L为User属性集。 (3) AA初始化。CA为每个AA设定一个类似于用户GID的标识符AID,为了保证每个AA都是合法的机构,CA为AA生成签名Asign。Asign=(AID‖UAID,Signkey),其中UAID为AA负责管理的属性集。 为属性集中的每个属性元素随机选择aij∈Zp,计算Aij=gaij。其中公钥APK={Asign,{Aij}},私钥ASK=aij。 数据拥有者采用k个密钥{k1,k2,…,kk}利用对称加密算法加密文件M={m1,m2,…,mk},文件密文为E(M)={Ek1(m1),Ek2(m2),…,Ekk(mk)},再用CP-ABE加密文件密钥。文件密钥加密过程如下: 数据拥有者首先确定好分层级访问树T,输入公钥GPK、APK、k个文件密钥,输出密文CT。 Ci=kiYsi=kie(g,g)∂si (3) (4) 在分级访问树中,每个(x,y)都对应一个多项式q(x,y),从R(x,y)开始,每个(x,y)的q(x,y)阶为:d(x,y)=k(x,y)-1。对于每个分级节点,q(x,y)(0)=q(x1,y1)(0)=si,多项式q(x,y)的其他系数随机选择。比如根节点R,qR(0)=q(x1,y1)(0)=s1。对于非分级节点,q(x,y)(0)=qparent(x,y)(index(x,y))。 集合Y为树中叶子节点的集合,对于任意的(x,y)∈Y,有: (5) (6) 对于其他节点,则有: C(x,y)i=e(g,g)∂(q(x,y)(0)+qchildj(0)) (7) 用户向AA发出私钥请求后,AA首先验证用户信息检查其是否在有效期范围内,如果身份有效,则根据用户属性生成私钥组件。 为每个属性值随机选择λi∈Zp,则: 用户从云端下载完密文后,需要得到共享文件的密钥K才能解密文件,首先是采用CP-ABE算法解密得到对称密钥,再通过对称算法解密共享文件。 类似于CP-ABE[21],解密运算如下: ① 若节点(x,y)为叶子节点时,令i=att(x,y),如果i∉S,DecryptNode(CT,SK,(x,y))=null。 如果i∈S,则有: e(g,g)rq(x,y) (0) (8) ② 若(x,y)为非叶子节点时,设Z为节点x的子节点,令Fz=DecryptNode(CT,SK,Z),S(x,y)为节点x的子节点集。 e(g,g)rq(x,y) (0) (9) ③ 如果S满足整个或者部分访问树,则: DecryptNode(CT,SK,(xi,yi))= e(g,g)rq(xi,yi)(0)=e(g,g)rsi (10) ④ 最后得到相关的密钥: (11) (12) ⑤ 利用ki解密Eki(mi)得到文件mi。若用户满足部分访问树,则可得到文件M中部分;若满足整个访问树,则可得到文件M的所有内容。 系统密钥由CA和AA共同生成,在以往的CP-ABE方案中,系统密钥只由CA生成,一旦CA被攻击,就会造成密钥泄露。在本方案中,如果CA被攻破,只会使得私钥的部分组件D被泄露,完整的私钥不会被泄露。如果部分AA机构被攻破,只会获得k个Di,解密几率还是非常小的,因此本方案中系统的密钥是安全的。 密文信息为Ci=kiYsi=kie(g,g)∂si,若要解密密文得到明文ki,必须恢复出e(g,g)αsi。对于一个不具备属性y的攻击者u1,即使与具备该属性的用户u2共谋,也不能得到密钥组件D;因为CA为每个用户产生的随机数r是不一致的。如果出现授权中心合谋攻击的情况时,只要CA中心的私钥组件D没有被泄露,方案仍旧是安全的。 根据第2节中设计的安全模型,对本文所提出的方案进行安全性证明。 定理1如果在任意的时间多项式算法中,Adversary不可能以不可忽略的优势ξ赢得挑战,则称本方案是选择明文攻击安全的。 选取双线性映射e:G×G→GT,随机选择a、b、c,其中a,b,c∈Zp。η∈{0,1},R∈GT。若R=e(g,g)abc时,η=1,否则η=0。 1) 初始化操作(Initialization)。Adversary将选择的访问结构W发送给Challenger。 2) 系统建立(Setup)。Challenger通过初始化算法setup,为Adversary提供公钥PK,Challenger随机选择a′∈Zp,a=a′+ab,则Y=e(g,g)a,h=gβ=B=gb。为每个属性值随机选择aij∈Zp,Aij=gaij,将PK发送给Adversary。 4) 挑战阶段(Challenge)。Adversary选择两条等长的消息M0和M1,Challenger通过访问结构W加密消息Mη,其中η∈{0,1},再将密文CT发送给Adversary。 C=MηYs=Mηe(g,g)as C′=hs=gβs 5) 查询阶段2(QueryPhase2)。重复查询阶段1。 6) 猜测阶段(Guess)。Adversary输出对于η的猜测η′(η′∈{0,1})。 如果η=η′,Challenger输出1,则R=e(g,g)abc,否则输出1。 最后赢得挑战游戏的优势为: 本文方案针对具有层次结构的文件提出多机构授权且隐藏树形访问结构的CP-ABE方案,本节从密文长度、用户密钥长度和加解密时间几个方面展开,同时与文献[7]的方案进行对比分析。 为了便于说明,定义以下符号:k表示文件分级个数;L*表示*的长度;|*|表示*的元素个数;AT表示除叶子以外的子节点集;i为AT中节点的子节点;Au为用户的属性集;AS为系统属性集;S表示具有层次结构访问树中的最小内部节点;tb表示双线性对运算;te表示群中的指数运算和乘法运算时间。 密文长度为(2|AS|+k)LG+(i|AT|+k)LGT。 用户密钥长度为(2|Au|+1)LG。 加密时间为(2|AS|+k)te+(i|AT|+2k)te。 解密时间为(2|Au|+1)tb+(2|S|+j|AT|+2k)te。 在文献[13]中,密文长度为(2|AS|+1)LG+LGT,用户私钥长度为(2|Au|+1)LG,加密时间为(2|AS|+2)te,解密时间为(2|Au|+1)tb。 若解密一个文件时,文献[13]中密文略短于本文生成的密文,用户私钥一样长,加密时间和解密时间也略低于本文方案。而本文方案可以同时加密K个文件,此时,本文方案明显优于文献[13]。且本文方案能够实现文件的分级访问控制。 本文利用多层次的树形访问结构加密文件,实现了文件的分级访问控制,同时,策略的隐藏防止了敏感信息的泄露,研究成果在DBDH假设下被证明是安全的。通过与其他方案的对比,本文方案在加密多个文件时具有明显的优势,同时多授权机构的使用不仅可以保护用户密钥的安全,也可实现用户的跨域访问。下一步,将重点研究如何减少解密运算量。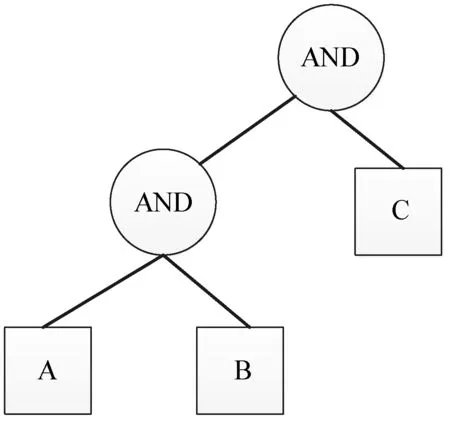
2 系统模型及安全模型
2.1 系统模型
2.2 安全模型

3 方案构造
3.1 初始化算法
3.2 加密算法

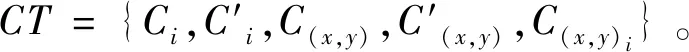
3.3 密钥生成


3.4 解密运算

4 安全性分析
4.1 密钥的安全性
4.2 抵抗合谋攻击
4.3 安全性证明
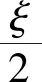



5 性能分析
6 结 语
