广义复合多尺度加权排列熵与参数优化支持向量机的滚动轴承故障诊断

2021-02-24丁嘉鑫王振亚姚立纲蔡永武

中国机械工程 2021年2期

丁嘉鑫王振亚姚立纲蔡永武

福州大学机械工程及自动化学院，福州，350116

0 引言

滚动轴承作为旋转机械应用广泛且容易损坏的零部件，对其进行故障诊断有着重要的理论和实际意义[1]。由于受负载、间隙、刚度、摩擦和冲击等非线性因素的影响，滚动轴承振动信号通常表征为非平稳和非线性等特性[2]。所以，众多衡量机械动力学系统的非线性时间序列复杂性方法相继被提出，并被应用于故障诊断领域，如近似熵、样本熵、排列熵和模糊熵等[3-5]。其中，排列熵(permutation entropy, PE)无需考虑时间序列的数值大小，而是对相邻样本点进行对比分析，获取相应特征信息，相较其他熵值方法更能捕获序列的微弱变化，并且该算法具有理论简单、抗噪能力强等优势，故在故障诊断领域应用较为广泛[4-5]。但PE算法仅利用时间序列的序数结构，忽视其幅值信息，因此，XIA等[6]在PE的基础上提出了加权排列熵(weighted permutation entropy, WPE)；ZHOU等[7]将其应用于滚动轴承故障特征提取过程。与PE类似，WPE仅考虑单一尺度上时间序列的复杂性和动力学突变，忽视了其他尺度上的有用信息，而YIN等[8]将WPE与多尺度熵相结合，提出了多尺度加权排列熵(multiscale WPE, MWPE)。但将MWPE应用于滚动轴承特征提取过程，仍存在以下不足：①MWPE的熵值估计偏差会随粗粒化尺度因子的增大而增大；②MWPE粗粒化过程忽略了其他粗粒化序列上的有用信息，从而影响熵值准确度。③MWPE进行粗粒化构造时，利用均值处理方式在一定程度上会中和原始信号的动力学突变行为，影响特征提取结果。针对以上不足，需要研发一种广义复合多尺度加权排列熵(generalized composite multiscale weighted permutation entropy, GCMWPE)新算法，通过采用广义复合粗粒化构造方式，以此克服MWPE算法存在的不足，并将上述方法应用于滚动轴承故障特征提取过程。

滚动轴承故障诊断的本质在于模式识别，支持向量机(support vector machine, SVM)在故障诊断领域应用广泛，并且取得较好的识别结果[9]，但该算法性能易受惩罚因子和核函数参数的影响。有学者将粒子群优化算法[10]、模拟退火算法[11]及人工鱼群算法[12]应用于SVM参数寻优过程，但上述寻优方法易陷入局部最优解并且寻优耗时。本文采用一种新颖元启发式优化算法——天牛须搜索(BAS)优化[13]对SVM参数进行寻优，在此基础上，提出了天牛须搜索优化支持向量机(beetle antennae search based support vector machine, BAS-SVM)。基于上述理论，建立一种GCMWPE、监督等度规映射(supervised isometric mapping, S-Isomap)[14]和BAS-SVM相结合的滚动轴承故障诊断模型，将其应用于实验数据分析过程。

1 广义复合多尺度加权排列熵

1.1 加权排列熵算法

排列熵(PE)只考虑序列的顺序结构特征，忽略了幅度特性。XIA等[6]在PE的基础上提出了加权排列熵(WPE)，具体算法流程如下。

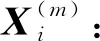
(1)

式中，τ为时延；m为嵌入维数。

(2)计算出每个子序列的权重值wi：

(2)

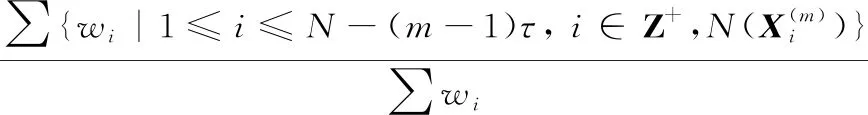
(3)

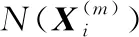
(4)计算时间序列X的加权排列熵WPE值：

(4)

1.2 多尺度加权排列熵算法

多尺度加权排列熵(MWPE)克服了WPE单一尺度分析的不足，能够从多个尺度全面表征时间序列复杂性，具体过程如下：

(1)对时间序列X进行粗粒化处理，得到粗粒序列y(s)=(y(s)(j))：

(5)

式中，s为尺度因子。

(2)计算不同尺度因子下粗粒化序列y(s)的WPE值：

MWPE(X,m,τ,s)=WPE(y(s),m,τ)

(6)

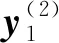
图1 MWPE粗粒化构造方式(s=2,3)

1.3 广义复合多尺度加权排列熵算法

图2 GCMWPE算法流程

针对MWPE存在的不足，本文作出以下改进：①采用复合粗粒化构造方式，考虑同一尺度下多个粗粒化时间序列的加权排列熵值，以此抑制由粗粒化时间序列变短而导致的熵值突变，得到更为精准的熵值特征。②将粗粒化过程的均值计算变更为方差计算，避免中和原始信号的动力学突变现象的发生。上述改进即为广义复合多尺度加权排列熵(GCMWPE)，流程如图2所示，具体步骤如下。

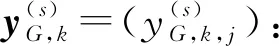
(7)

j,k,s∈Z+

(3)均化同一尺度下多个WPE值，即可得到s尺度下的GCMWPE值，对应表达式如下：

(8)

GCMWPE算法需人为设定以下4个参数：样本长度N，嵌入维数m，尺度因子s和时延τ。其中，s的取值目前尚无选定标准，通常设置为s>10，本文设定s=20。时间序列长度应满足N>200 s，故本文选取N=4096。m对GCMWPE具有一定影响，若m过小，相空间重构的向量包含较少信息，算法将无法有效监测序列的动力学突变；反之，若m过大，相空间重构的向量会忽略序列的细微变化，并且增加运算时间。通常设定m的取值范围为[4, 7]。时延τ对熵值计算影响较小，一般设定为τ=1[7]。

1.4 实验验证

为探究嵌入维数m对所提GCMWPE算法的影响，将其应用于凯斯西储大学轴承数据实验分析[15]。实验轴承为6205-2RS深沟球轴承，利用电火花技术在轴承表面进行单点故障加工，其中，故障直径为0.3356 mm，故障深度为0.2794 mm。本次实验设置电机转速为1797 r/min，负载为0，在采样频率为12 kHz的条件下，分别采集轴承正常和具有外圈故障振动信号各20组，每组信号包含4096个采样点。

将不同嵌入维数m(分别取4, 5, 6, 7)下的GCMWPE应用于两种状态轴承数据分析过程，两种状态的熵值均值曲线以及对应的线性拟合分别如图3a和图3b所示。由图3可知：①当嵌入维数m较小(为4或5)时，GCMWPE熵值拟合线较为平缓，无法体现多尺度的优势；而当嵌入维数m较大(为7)时，相空间重构的向量会忽略序列的细微变化，导致两种状态熵值曲线较为接近，无法有效区分故障类型(两种状态下轴承的GCMWPE熵值均值曲线对比如图4所示)。因此，本文设定m=6。②同一m下，第一个尺度上，正常状态的熵值高于外圈故障状态。原因在于，当轴承处于正常状态时，振动信号波动较为随机，信号的无规则性较高，自相似性较低，故熵值较大；而当轴承出现局部故障时，振动信号波动出现一定规律性，信号的规则性和自相似性较高，故熵值较小,因此，GCMWPE能够监测轴承是否发生故障。

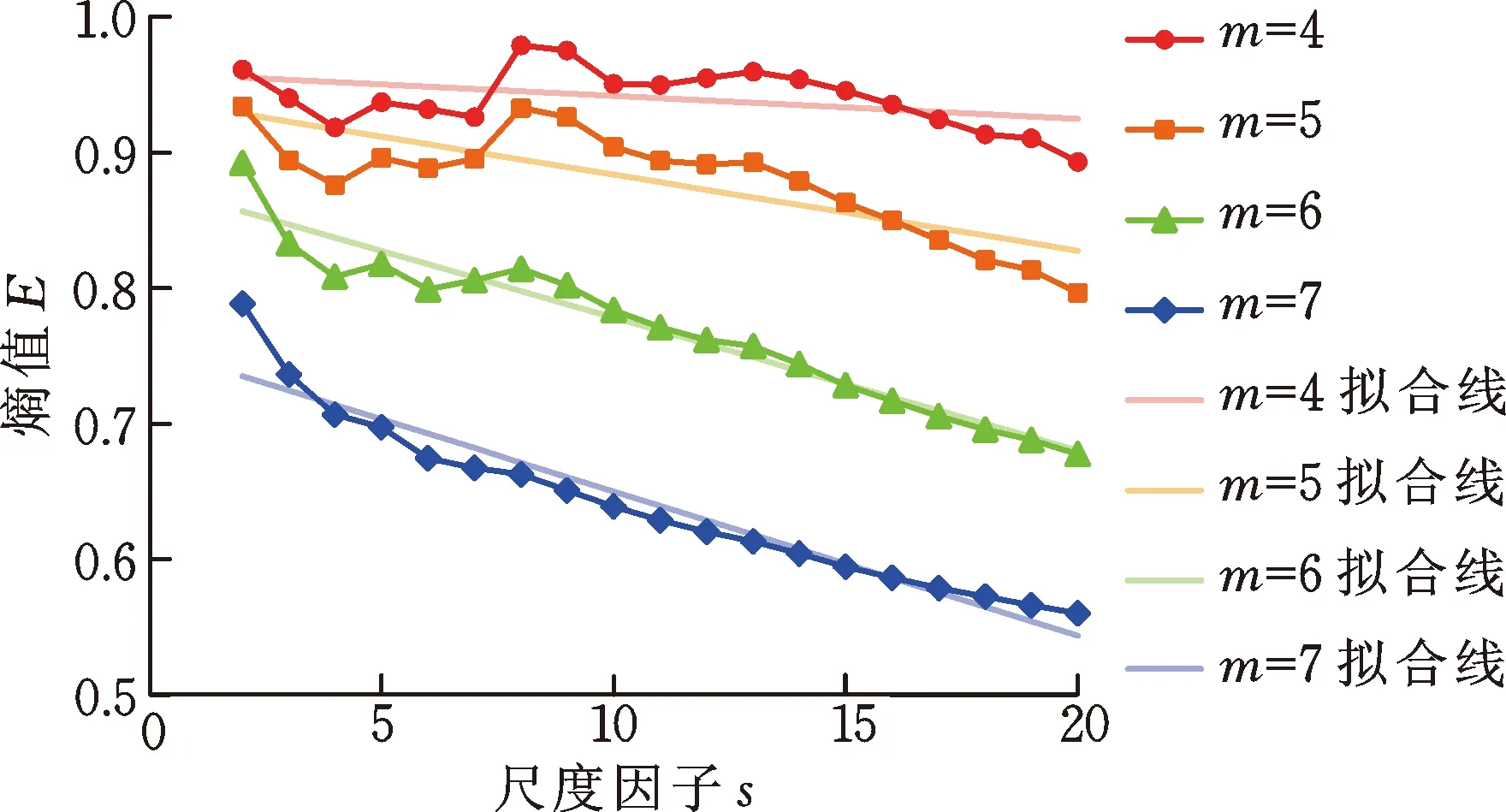
(a) 正常信号分析结果

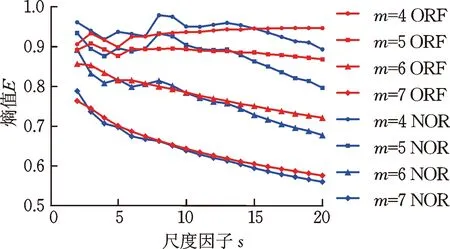
图4 GCMWPE对两种信号分析结果

2 BAS算法和BAS-SVM

2.1 BAS算法

BAS算法通过模拟自然界天牛根据触角接受的气味强度进行搜索食物，从而获取全局最优解，具体步骤如下。

(1)初始化参数。初始两须距离p(0)，初始步长δ(0)，迭代次数T，初始位置为u(0)。

(2)计算两须坐标。左右须坐标分别如下：

(9)

p(t)=0.95p(t-1)+0.01

(10)

(11)

其中，sgn(·)为符号函数，δ(t+1)为t+1次迭代时的移动步长，其表达式为

δ(t+1)=0.95δ(t)

(12)

(4)判断是否达到最大迭代次数，若满足，则计算终止；否则，继续循环。

2.2 BAS-SVM

针对支持向量机(SVM)算法性能易受惩罚因子c和核函数参数g影响的问题，本文研发一种天牛须搜索优化支持向量机(BAS-SVM)新算法，流程如图5所示，具体过程如下。

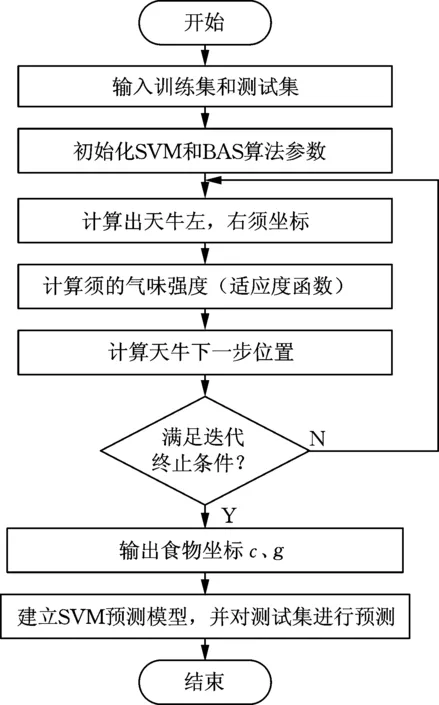
图5 BAS-SVM流程

(1)输入训练集与测试集样本，并对两个样本集分别进行归一化处理。初始化BAS和SVM参数，包括初始两须距离p(0)，初始步长δ(0)，迭代次数T，初始位置为u(0)；参数c和g的取值范围为[0.001, 100]，选用径向基函数。

(2)利用式(9)计算出天牛左右两须的坐标。

(3)计算出天牛左右两须的气味强度。其中，以训练样本三折交叉验证后的平均识别率为其适应度函数值。

(4)利用变步长法(即式(11))确定天牛下一步的位置。

(5)判断是否满足最大迭代次数，若满足，则计算终止；否则，继续循环。

(6)输出天牛搜索食物的位置(即为最优c和g)，并将最优参数建立SVM预测模型，并利用该模型对测试集样本进行测试。

3 滚动轴承故障诊断实验分析

3.1 故障诊断模型

本文提出一种广义复合多尺度加权排列熵(GCMWPE)、监督等度规映射(S-Isomap)和BAS-SVM相结合的滚动轴承故障诊断方法，诊断流程如图6所示，具体步骤如下。

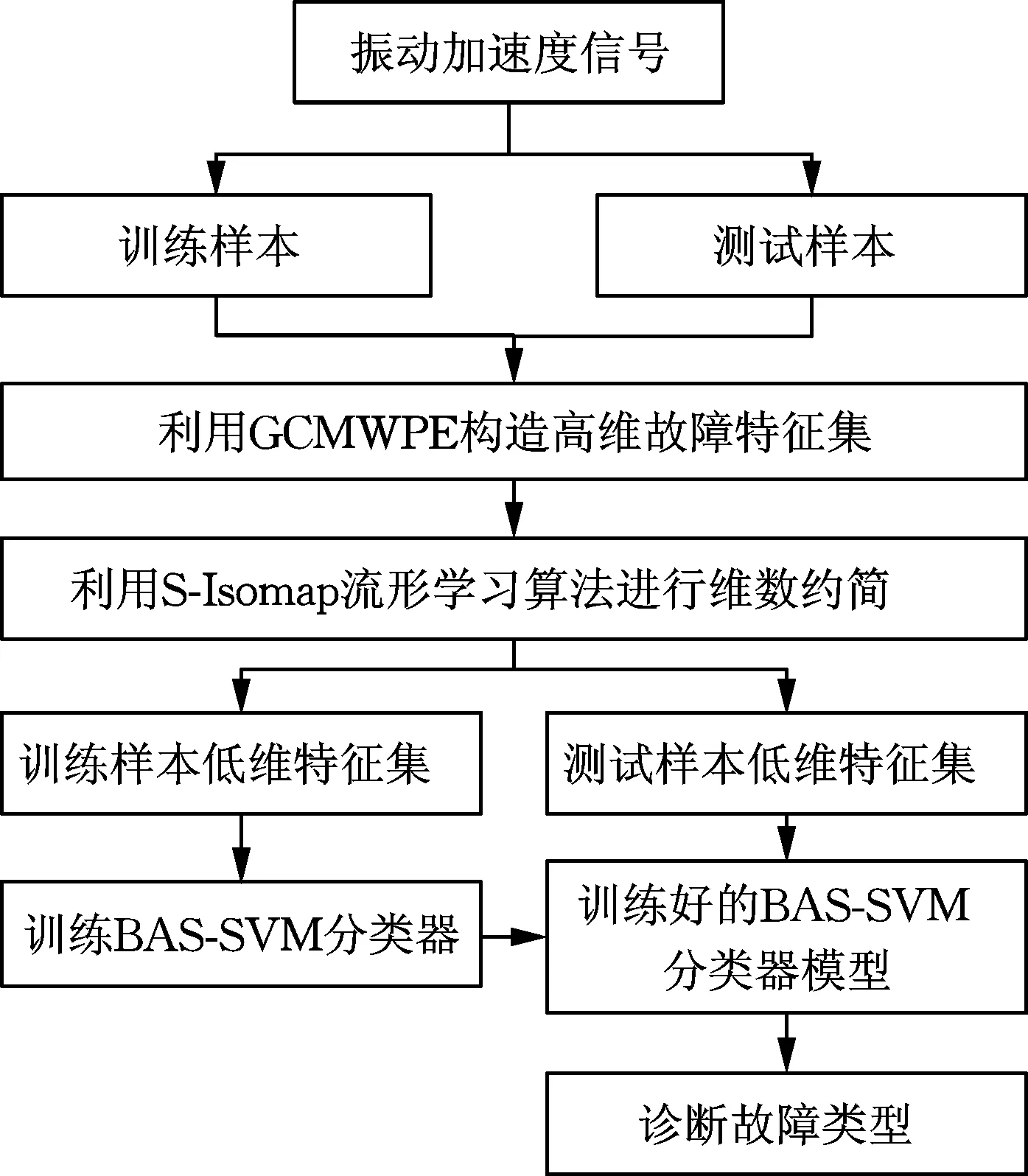
图6 滚动轴承故障诊断流程

(1)信号采集。在一定采样频率fs下，利用加速度传感器分别采集滚动轴承不同状态下的振动加速度信号，并将其分为测试和训练样本集。

(2)计算高维故障特征。利用GCMWPE算法对训练样本与测试样本信号进行熵值特征提取，合并成高维故障特征集。

(3)降维处理。由于GCMWPE高维特征集存在冗余特征，影响最终识别效果，故利用S-Isomap流行学习算法对该特征集进行维数约简，获取低维、易于区分故障类型的敏感特征集。

(4)故障识别。利用BAS-SVM分类器对GCMWPE+S-Isomap低维故障特征集进行训练与测试，诊断出测试样本各故障类型。

3.2 故障诊断实例

为模拟滚动轴承实际工作条件，利用Spectra Quest公司研发的动力传动系统故障诊断实验台进行实验数据的采集，实验平台如图7所示。本次实验中，输入轴转速为20 Hz，负载为0，在采样频率3000 Hz下，利用加速度传感器分别采集滚动轴承4种状态振动加速度信号各100组，即正常(normal, NOR)、外圈故障(outer race fault, ORF)、内圈故障(inner race fault, IRF)和滚动体故障(ball fault, BF)。每组信号包含4096个采样点，4种状态共计400组样本信号，对应时域波形如图8所示。其中，每种状态随机选取20组样本作为训练样本，剩余80组样本作为测试样本，4种状态共计80组训练样本、320组测试样本。

图7 滚动轴承故障诊断实验平台

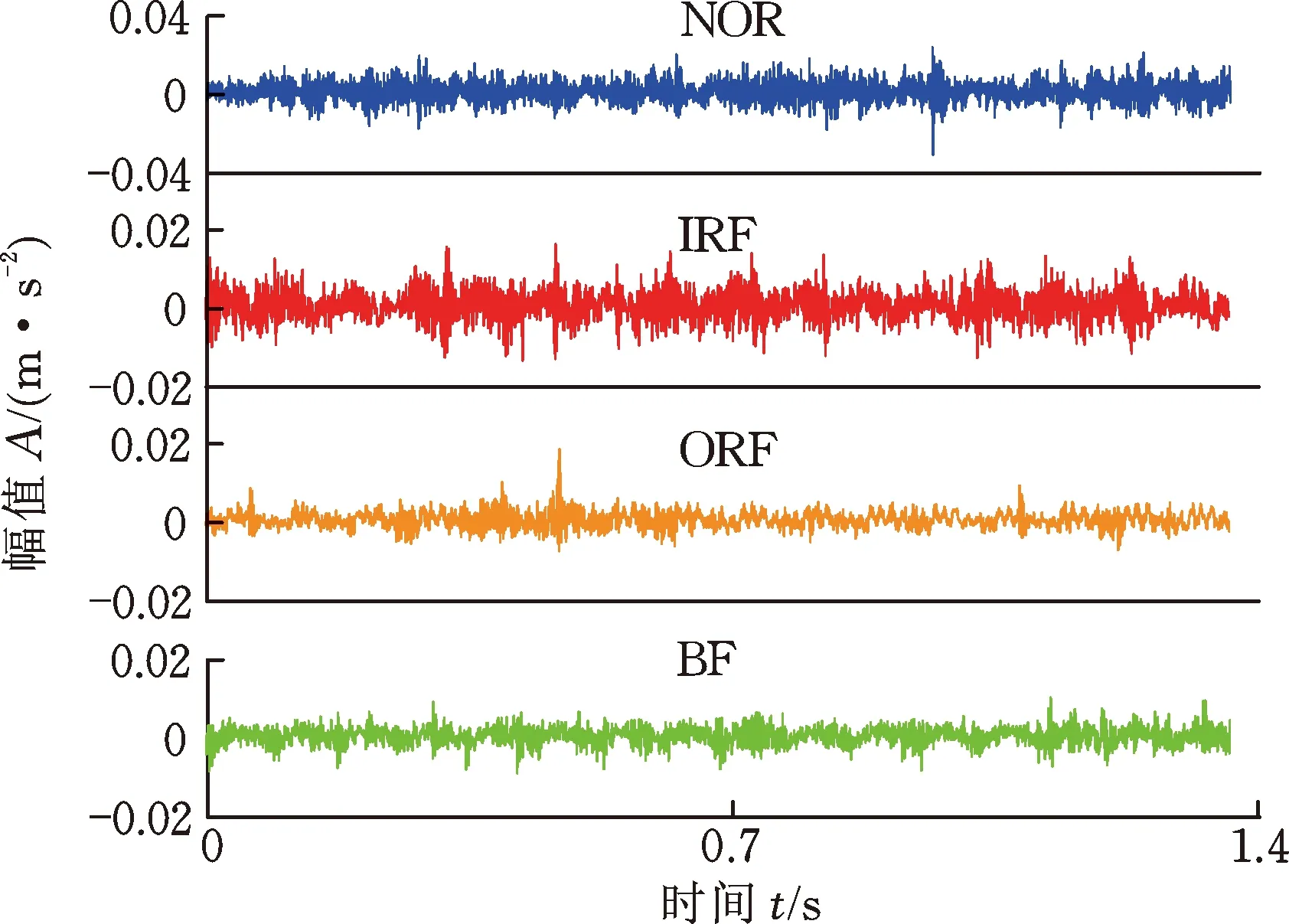
图8 时域波形

3.2.1特征提取

首先，利用GCMWPE对振动信号进行熵值特征提取，构建原始高维特征集。为验证所提方法有效性，将其与GMWPE(仅采用广义粗粒化构造方式，未采用复合粗粒化构造方式，即式(7)中k=1，其余与GCMWPE相同)、MWPE和复合多尺度加权排列熵(composite multiscale weighted permutation entropy, CMWPE)[16]三种算法进行比较。4种算法在滚动轴承不同状态下的熵值均值曲线见图9。其中，设置对比方法的尺度因子s=20，时延τ=1，嵌入维数m=6。

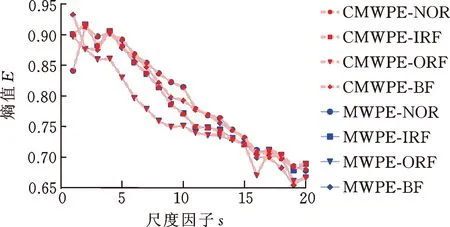
(a) MWPE和CMWPE均值曲线

由图9可知：①与MWPE和CMWPE相比，本文所提的GMWPE和GCMWPE方法提取得熵值均值曲线较为平滑，并且能够有效将4类样本区分开，体现出广义粗粒化构造方式的优越性。②就起始尺度而言，MWPE和CMWPE得到的滚动轴承4种状态中滚动体状态熵值最大，而GMWPE和GCMWPE得到的滚动轴承4种状态中正常状态熵值最大。就实际工况而言，当滚动轴承处于正常状态时，振动信号波动较为随机，信号的无规则性较高，自相似性较低，故熵值较大；而当轴承出现局部故障时，振动信号波动出现一定规律性，信号的规则性和自相似性较高，故熵值较小，故相比MWPE和CMWPE，GMWPE和GCMWPE算法更适用于滚动轴承的特征提取过程。③GMWPE和GCMWPE算法对滚动轴承每种状态分析得到的熵值均值曲线较为接近，但随机选取1组信号进行分析时(图10)，GMWPE提取的熵值曲线较GCMWPE波动较大，表明采用复合粗粒化(即考虑同一尺度多个粗粒化序列)的GCMWPE提取的熵值较采用原始粗粒化(即仅考虑同一尺度下一个粗粒化序列)的GMWPE算法更为稳定；同理，CMWPE和MWPE对随机选取的熵值分析结果(图10b)也能得到相同的结论。上述分析验证了将所提GCMWPE应用于滚动轴承故障特征提取的可行性和优越性。

(a) 随机1组信号的GMWPE和GCMWPE熵值曲线

3.2.2维数约简

GCMWPE提取的故障特征集具有高维、非线性和冗余等特性，直接利用BAS-SVM进行故障识别，会增加识别时间甚至影响识别效果，因此，本文采用S-Isomap算法对其进行降维处理，提取出易于区分故障类型的低维特征集。同时，为了进行对比，利用该流形学习算法对MWPE、CMWPE和GMWPE进行维数约简。S-Isomap算法对4种特征集的降维结果如图11所示。其中，通过交叉验证的方式确定各参数(表1)。

表1 S-Isomap参数设置

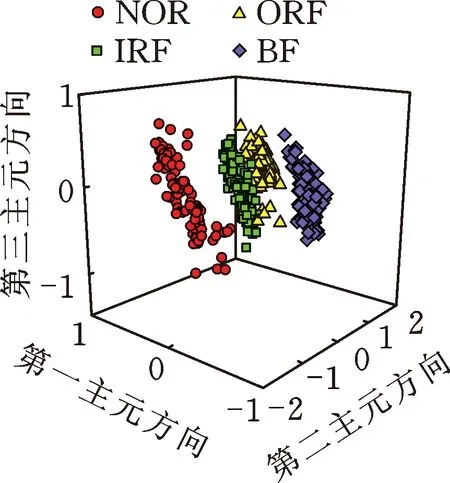
(a) S-Isomap对MWPE降维结果

由图11可知：①MWPE和CMWPE降维结果中，内圈故障和外圈故障状态的样本出现了混叠现象，并且4类样本较为分散；而GMWPE和GCMWPE的降维结果中，可以将4类样本基本分离开，并且每类样本拥有较好的聚类效果，以此进一步验证广义粗粒化构造方式的优势。②与GMWPE相比，GCMWPE的降维结果中可以将4类样本完全分离开，未出现GMWPE中个别样本远离聚类中心现象，表明采用复合粗粒化构造方式的GCMWPE算法能够提取出更为稳定的熵值特征信息。③S-Isomap对GCMWPE特征集的降维结果中，能够有效将4类样本完全区分开，4类样本聚集性较好，降维效果最佳，这说明本文所提GCMWPE与S-Isomap相结合的特征提取方式能够有效提取出易于区分滚动轴承故障特征信息的低维、敏感特征集。

3.2.3模式识别

为量化上述4种降维后特征提取效果，分别将其输入BAS-SVM分类器中进行诊断识别，识别结果和混淆矩阵如图12所示。其中，设置BAS-SVM算法中初始两须距离p(0)= 2，初始步长δ(0)=4，迭代次数T=100。

由图12可知：①BAS-SVM分类器对GCMWPE(CMWPE)+S-Isomap的平均识别率比GMWPE(MWPE)+S-Isomap高出1.25%(0.625%)，验证了复合粗粒化的优越性。②BAS-SVM分类器对GCMWPE(GMWPE)+S-Isomap的平均识别率比CMWPE(MWPE)+S-Isomap高出2.5%(1.875%)，体现了广义粗粒化的优势。③本文所提GCMWPE+S-Isomap特征集的故障识别率达到100%，能有效、精准地识别出滚动轴承故障类型。

为验证所提BAS-SVM分类器的优越性和高效性，将其与粒子群优化支持向量机(particle swarm optimization SVM, PSO-SVM)、模拟退火优化支持向量机(simulated annealing SVM, SA-SVM)和人工鱼群优化算法支持向量机(artificial fish swarm algorithm SVM, AFSA-SVM)三种分类器进行对比，4种分类器(参数设置见表2)对上述4种降维后特征集的识别结果如图13所示，对应识别时间见表3。其中，本次实验各算法编译于MATLAB 2017软件，运行环境如下：Intel (R) Core (TM) i7-8550 CPU, 16 GB RAM, Windows 10系统。

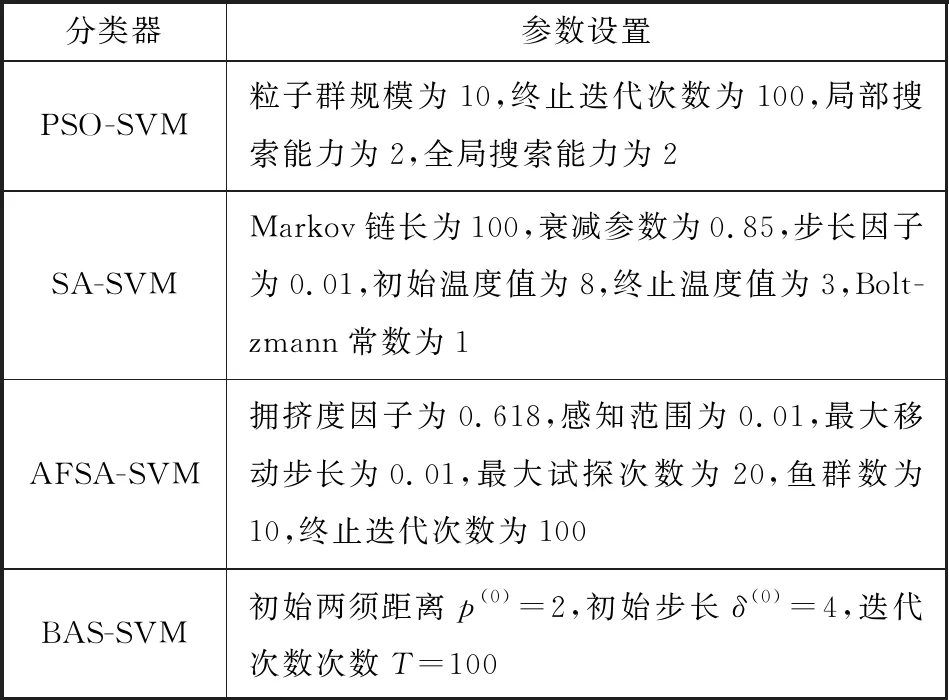
表2 3540Fe基粉末化学成分

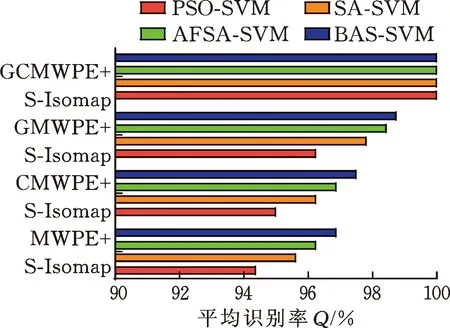
图13 滚动轴承故障诊断模型

表3 平均识别时间

由图13和表3可知：①就每种特征集而言，BAS-SVM均具有较好的故障识别效果，以此验证BAS-SVM分类器在模式识别方面的优越性。②PSO-SVM、SA-SVM和AFSA-SVM分类器对4种特征集的平均识别时间分别是BAS-SVM分类器用时的8.039倍、16.670倍和19.655倍，体现了BAS-SVM分类器的高效性。③所提GCMWPE+S-Isomap方法提取的故障特征在每种分类器下的故障识别率均为100%，进一步验证所提故障诊断方法的优越性。