基于k近邻和数值模拟的锅炉炉膛温度场在线重建

郭子申，董美蓉，叶 托，龙嘉健，陆继东

（1.华南理工大学 电力学院，广东 广州 510640；2.广东省能源高效低污染转化工程技术研究中心，广东 广州 510640）

炉膛温度场是锅炉设备安全稳定运行控制中的关键参数，其分布直接影响锅炉稳燃、结渣和污染物排放[1]。温度场分布不合理会引起锅炉运行出现燃烧不均匀、火焰燃烧中心偏斜、火焰刷墙等问题[2-3]。重建温度场可实时监测炉膛燃烧状态，为运行人员提供火焰信息，实现精细化燃烧调整，保证锅炉的安全、可靠、经济运行。

近年来很多学者采用声学法与光学法对整个锅炉炉膛的温度场进行在线测量[4-5]。周怀春等[6-8]研发了一套锅炉三维温度场可视化检测系统，采用CCD成像技术与多种算法修正，能够较准确地反映出炉内三维温度场分布。李艳秋、刘石等[9]基于三维变分的声学层析成像法对锅炉炉膛的4种温度场模型进行三维温度场重建，结果表明该声学重建算法精度高，并具有良好的抗噪能力。然而这些非接触式测温设备在实际使用中存在布置困难、价格昂贵并且容易受到环境干扰等问题。

建立燃烧过程的机理模型并采用数值方法求解可以准确地获取锅炉内温度场、速度场的分布情况，不仅加深了人们对锅炉炉膛内部燃烧过程的认识，而且通过模拟结果可以对锅炉燃烧过程进行优化调整[10-13]。由于炉膛的空间尺寸和反应的复杂性，得到模拟结果往往需要数个小时的迭代计算，因此当锅炉机组运行工况改变时，难以实时反映炉内温度场的分布情况。

本文提出一种基于k近邻（k-nearestneighbor，kNN）与数值模拟的锅炉炉膛温度场在线重建算法，采用某330 MW四角切圆锅炉的多工况数值模拟案例库作为数据源，结合kNN算法与八叉树数据结构，将整个模拟案例库作为样本集。利用数值模拟结果中的炉内燃烧信息，对锅炉炉膛温度场的不同截面进行在线重建，快速获得炉内温度场分布。并通过对实时重建结果与模拟结果进行误差分析，验证该温度场重建算法的准确性。

1 研究对象及数据来源

图1为某330 MW亚临界参数的四角切圆锅炉尺寸示意图。锅炉高53.7 m，炉膛横截面尺寸为13.74 m×14.07 m。其燃烧设备为四角布置，切向燃烧，燃烧器共分16层，上中下3组，燃尽风人工上下摆动，其余各层喷口均可机械摆动。

表1为从DCS系统的历史数据中划分出的25个锅炉稳定运行工况的主要参数，表2为煤粉燃烧过程数值模拟计算采用的主要模型与方法，在保证模拟结果可靠性与正确性的基础上，采用Fluent软件对锅炉煤粉燃烧过程进行多工况数值模拟，并将其模拟结果构建数值模拟案例库，案例库结构如图2所示。每个工况案例中包含模拟结果的网格点坐标（X、Y、Z）、温度场（T）、速度场（V）、浓度场（O2、CO、CO2）以及氮氧化物场（NOx）等信息。

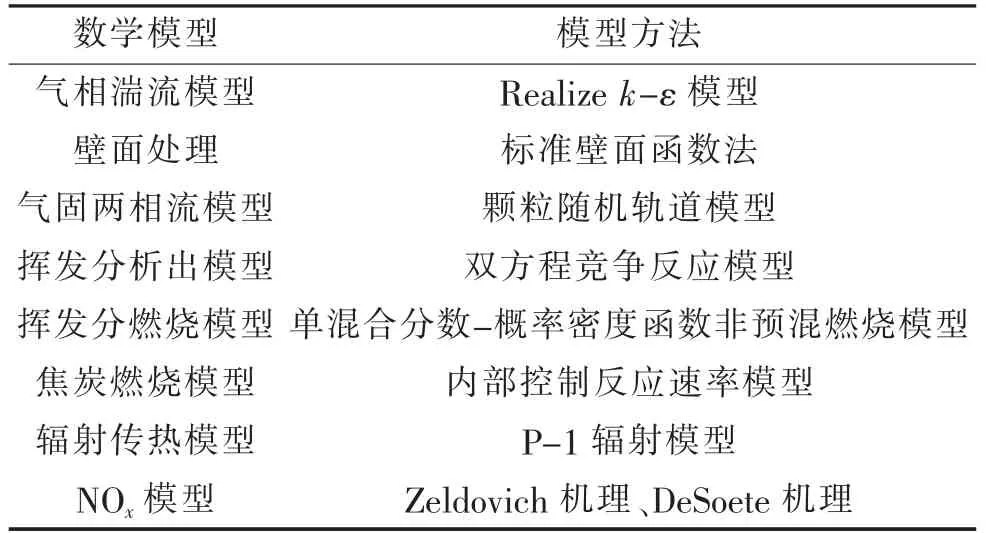
表2 数值模拟计算模型

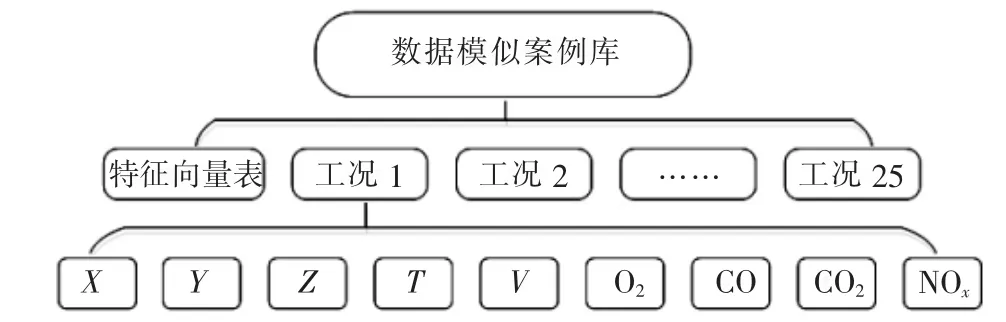
图2 数值模拟案例库结构示意图

表1 锅炉稳定运行工况主要参数

2 炉膛温度场在线重建

2.1 k NN算法

kNN算法的应用思想是给定一个模拟数据集，对输入的实时工况，在数据集中找到与该工况最邻近的k个模拟案例，这k个案例的多数属于某个类，就把该输入工况分为这个类[14-16]。kNN算法的关键问题是距离和k值的选取。距离表示数据集中各个案例与当前工况的近似程度，k值的选择反映了对近似误差与估计误差之间的权衡。距离公式如下：

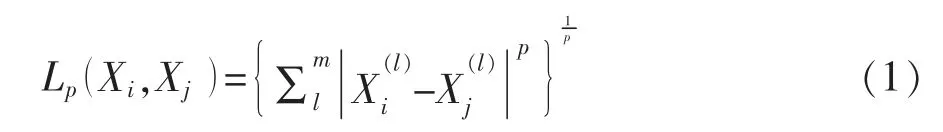
式中：Xi，Xj表示特征向量；m为样本个数；p≥1，l=1，2，…，m。当p=1时距离为曼哈顿距离；当p=2时距离为欧氏距离。

首先以主汽流量、一次风量、二次风量、给煤量、煤质低位热值为特征向量，在多工况数值模拟案例库中采用曼哈顿距离找到与实时工况最近邻j个工况的模拟结果组成空间数据集Nj，公式如下：式中：Pi表示模拟数据集；（Xij，Pij）表示与当前工况最近邻的模拟数据工况。

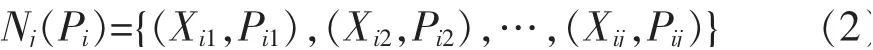
其次应用kNN回归算法，将重建网格点在空间数据集Nj中采用欧氏距离寻找最近邻的k个模拟数据点，求取温度均值并赋值给重建网格点，公式如下：

式中，Ft表示最近邻k个模拟数据点的温度场信息，t=1，2，…，k。

2.2 八叉树数据结构

由于kNN算法采用全局搜索，当重建网格点在进行空间数据集Nj中进行最近邻回归寻值时，循环次数多，计算耗时较长，因此将kNN算法与八叉树数据结构结合起来。八叉树作为一种空间数据结构，其作用主要是对锅炉三维空间模型中网格点的存储及快速寻值。本文采用八叉树结构优化传统kNN算法的数据存储结构，以提高kNN算法全局寻值速度及数据存储效率，八叉树划分原理如图3所示。

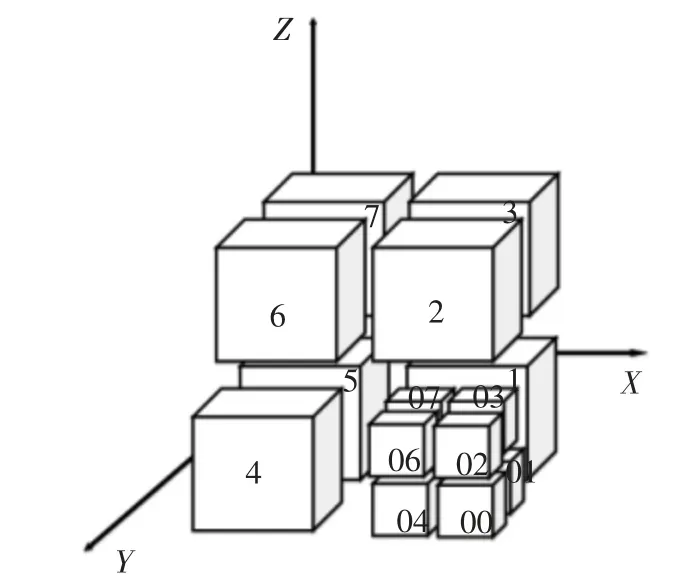
图3 八叉树划分原理示意图

首先通过锅炉实际尺寸确定八叉树立方体结构的边界范围，参数范围如下：

然后对原始立方体沿着3个不同方向划分成8个子节点，并设置其节点深度，从而控制八叉树的层数，每个子节点中包括节点深度、节点中心坐标、数据列表、子节点等。

2.3 评价

为了分析重建算法的准确性，采用平均相对误差（EMP）与相关系数（R2）从总体上评价温度场的重建效果，公式如下：

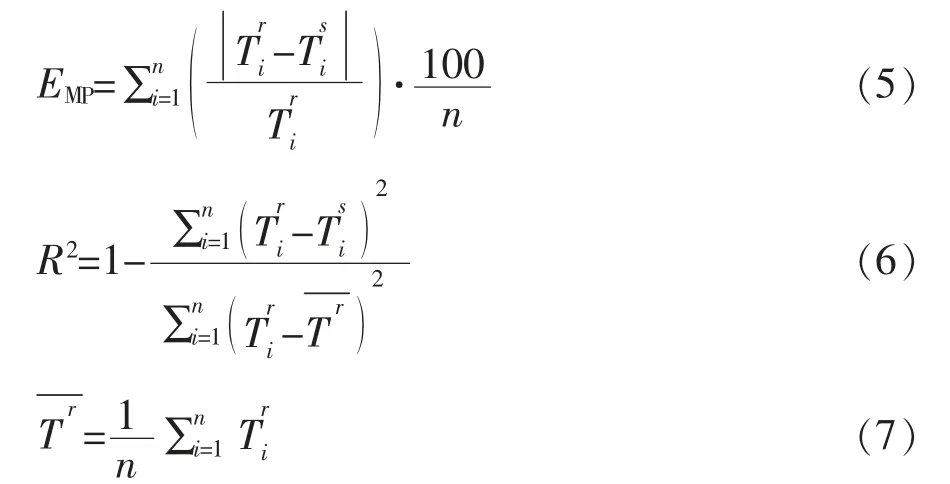
式中：Tr和Ts分别为重建结果与模拟结果的温度值，K；表示重建温度场的平均值，K。

3 结果与分析

为了更好实现炉膛温度场的在线重建，以稳定运行时间最长的实时工况71.2%与实时工况78%为例，首先对kNN回归算法中的k值与八叉树的节点深度d进行参数寻优；然后结合最佳k值与最佳节点深度，对各工况的不同截面位置进行温度场在线重建。

3.1 kNN回归算法参数寻优

以工况78.0%为例，对kNN回归算法进行参数寻优，分别取k=1，2，3，…，14对截面X=0 m，Y=0 m，Z=36.4 m（炉膛折焰角高度）进行温度场重建，重建结果评价如图4、图5所示。当k小于8时，平均相对误差随着k的增大而减小，相关系数随着k的增大而增大；当k大于8时，平均相对误差随着k的增大而增大，相关系数随着k的增大而减小。因此当k=8时，X=0 m、Y=0 m、折焰角横截面的相关系数最大且平均相对误差最小，重建效果最好。

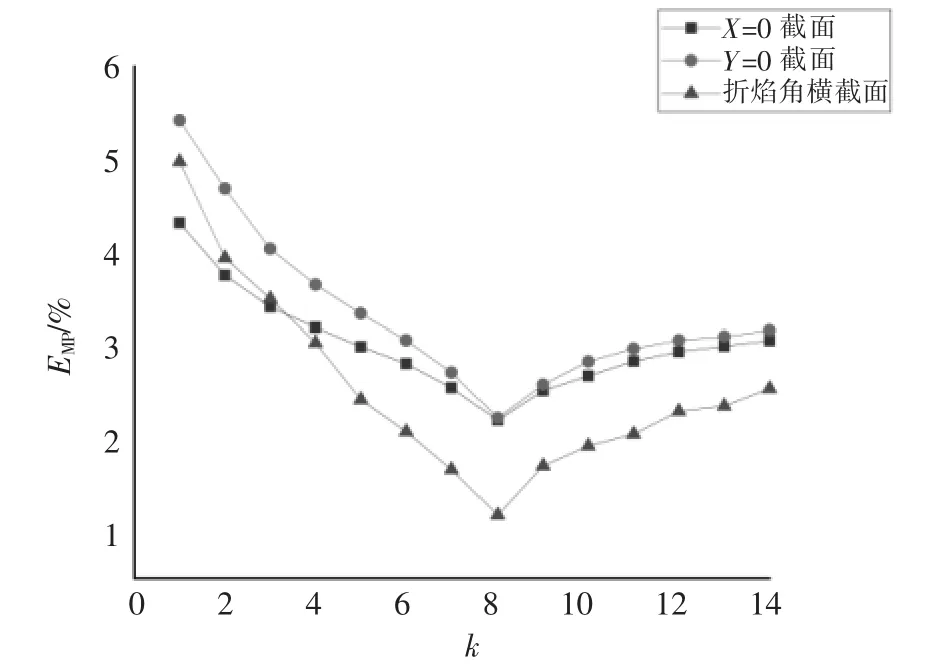
图4 不同k值情况下E MP的趋势图

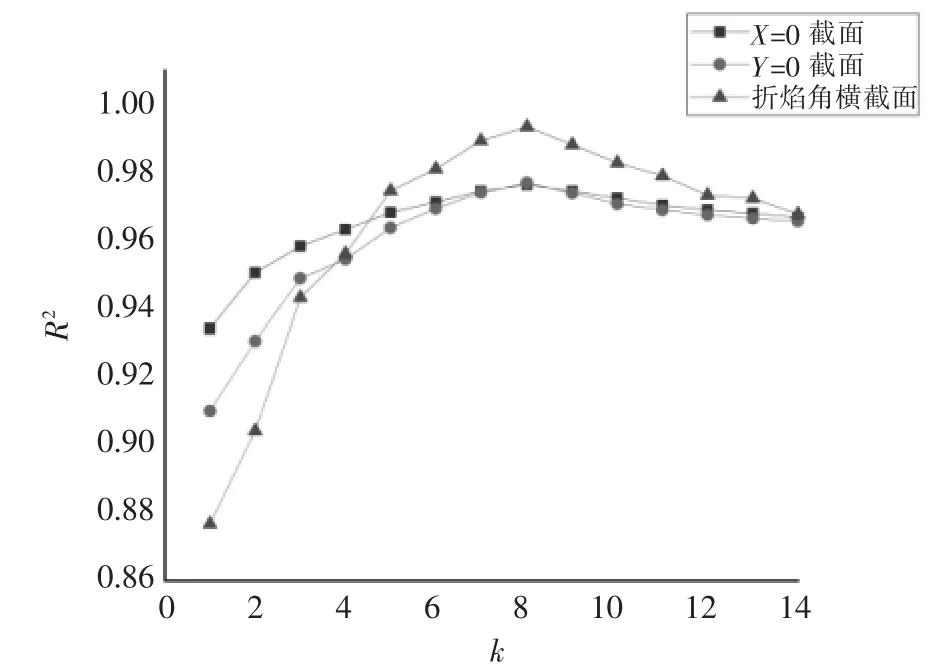
图5 不同k值情况下R2的趋势图

3.2 节点深度对重建时间的影响

采用计算机硬件配置为Intel E5-2630，2.20 GHz CPU，64 GB内存，Windows10操作系统。以工况78%为例，分别取八叉树数据结构节点深度d=1，2，3，对不同截面类型进行多次重建取平均时间t，见表3。随着节点深度的不断增大，重建时间缩短。当d=3时，重建锅炉纵截面、横截面的平均时间分别为3.14 s、0.32 s，此时八叉树叶节点中的数据列表元素个数均小于64，若继续划分子节点，则叶节点中元素个数不足8个，由于在进行k近邻回归计算时最佳k值为8。因此在进行温度场重建时，可选取八叉树节点深度为3，以实现锅炉炉膛温度场的在线重建。

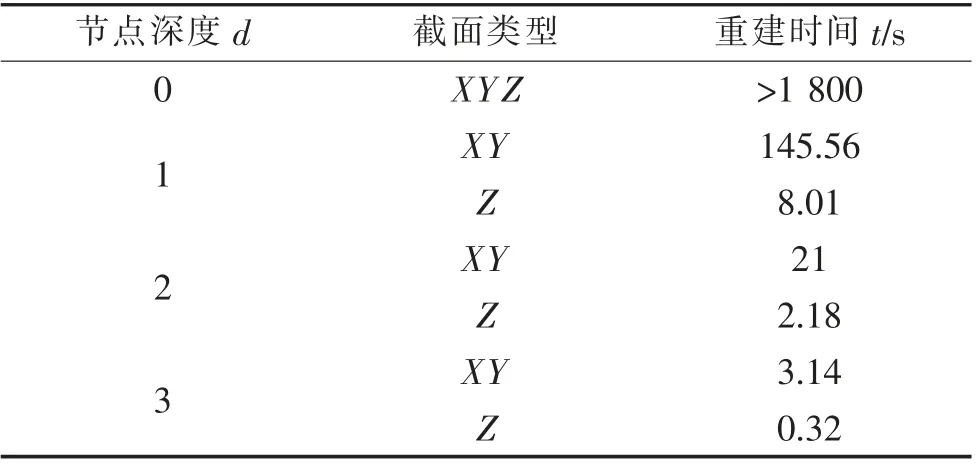
表3 重建时间对比

3.3 同截面位置的重建结果与分析

为验证不同截面位置的重建效果，以稳定运行时间最长的实时工况71.2%与实时工况78%为例，分别对截面位置为0 m、-1 m、1 m的XY截面和高度位置为20.9 m（一次风口高度）、27.1 m（OFA3燃尽风喷口高度）、36.4 m（折焰角高度）的Z截面进行温度场重建。

图6与图7是分别运用OpenGL图形接口框架与Origin软件绘制的78%实时工况条件下数值模拟结果与重建结果的对比图，可以看出，两者温度场整体分布规律大致相同，火焰燃烧中心位置基本保持一致。为了更准确地评价重建效果，各个截面的重建结果评价指标如表4所示。重建结果的平均相对误差均在5%以下，R2均在0.92以上，结果表明重建结果与模拟结果的温度场分布一致，重建误差在工程应用允许的误差范围之内。

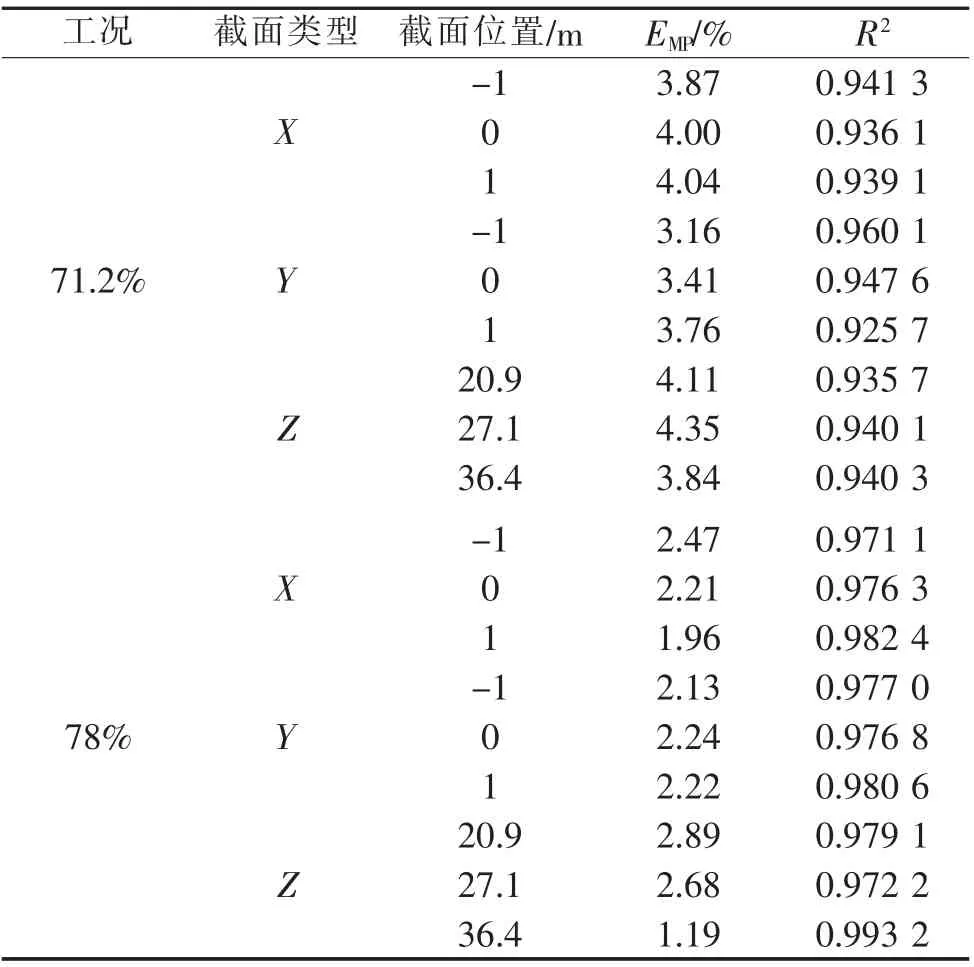
表4 不同截面重建结果误差评价

图6 工况78%-X截面数值模拟结果与重建结果对比图

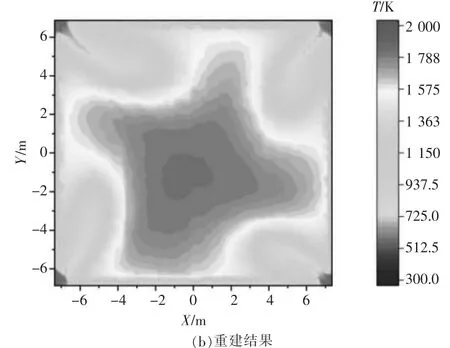
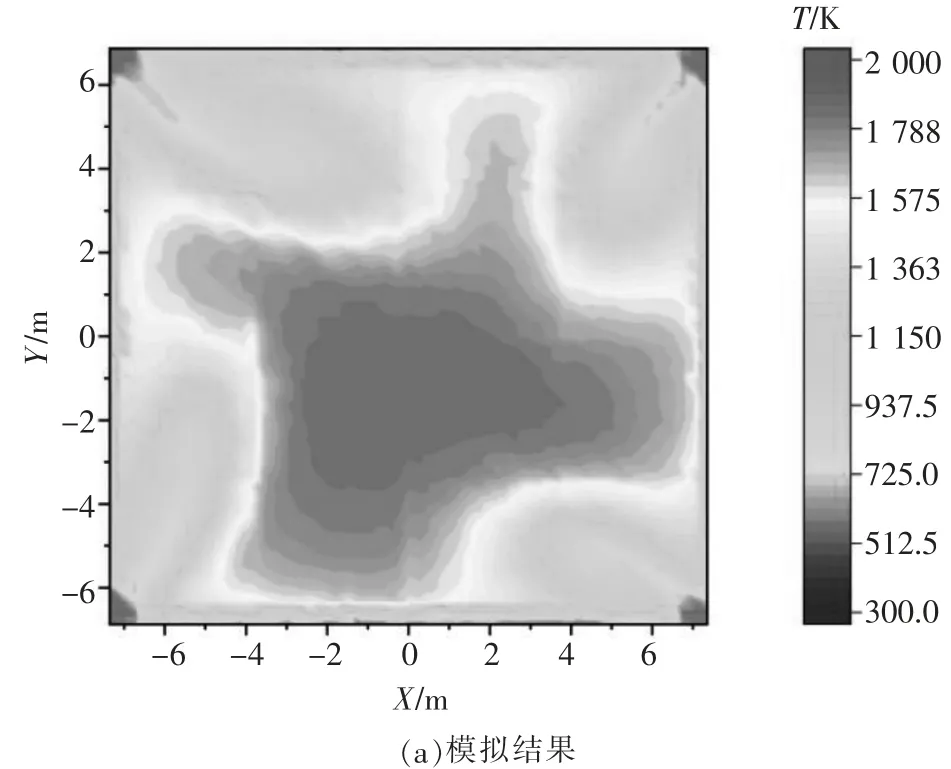
图7 工况78%-Z=27.1 m模拟结果与重建结果对比图

4 结论

以多工况数值模拟案例库为数据源，提出一种kNN算法与八叉树数据结构相结合的锅炉温度场在线重建算法，实现了对锅炉炉膛温度场的实时监测。得到以下结论：

（1）当k取值为8，八叉树节点深度为3时，各截面重建效果最好，重建锅炉纵截面、横截面的平均时间分别为3.14 s及0.32 s，平均相对误差最大为4.35%，相关系数最小为0.925 7。

（2）在锅炉运行过程中通过实时匹配数值模拟案例库，对温度场进行在线重建，电厂运行人员可以间接地通过温度场分布情况对炉内燃烧做出对应的配煤配风调整。为了更好地重建锅炉炉膛温度场，需要进一步将电厂DCS系统的炉膛实时数据应用到重建算法中。