考虑无功补偿的10 kV 馈线拓扑数据驱动辨识方法
2021-02-24汪子晨陈新建
汪子晨,于 杰,杨 坚,陈新建,吴 浩,鞠 平
(1.浙江大学 电气工程学院,杭州 310027;2.国网浙江省电力有限公司台州供电公司,浙江 台州 318000)
0 引言
近年来,配电网中安装了大量的量测装置,积累了海量的稳态数据[1]。分析这些数据得到的结论广泛应用于电网规划与运行[2]、配电网短期/长期负荷预测[3-4]、防窃电管理[5]、配电网故障管理[6]等。
中压配电网系统(6~10 kV)结构细琐,拓扑复杂,且由于运行方式多变,网络拓扑重构后未及时更新等原因[7],GIS(地理信息系统)记录的配电网拓扑信息往往存在错误。另一方面,网络当前的拓扑结构是DMS(配电管理系统)中大部分功能的基础,如状态估计[8]、潮流计算、自动电压控制等。此外,如阻抗估计[9]、相辨识[10]、变压器辨识[11]、二次电路建模[12]等其他应用,也依赖于网络拓扑结构。因此,利用配电网量测数据,采用数据驱动的方式,辨识中压配电网拓扑具有较好的应用需求,其核心是中压馈线拓扑辨识。
现有数据驱动的馈线拓扑辨识方法种类繁多,其中研究较深入的有以下三类。第一类,通过智能电表量测电压曲线的相关性分析辨识相邻电表,预测各个电表的上下游位置关系,进而纠正GIS 中的拓扑错误,如文献[13-14]。第二类,将配电网建模为一个概率几何模型,通过解正则化线性回归问题,将寻找某节点的邻域转化为计算各节点电压时序数据的关联系数向量,从而构建线路拓扑,如文献[15-16]。第三类,利用电压降和线性回归的关系为线路中每个节点寻找配对节点,进而根据节点配对信息还原馈线拓扑,如文献[11,17]。此外,还有一些文献尝试从其他角度切入,如文献[18]利用电压和功率量测数据估计电压敏感矩阵并依此计算节点间距离矩阵,再利用Prufer 序列辨识馈线拓扑;文献[19]利用μPMU(微型同步相量量测单元)采样数据,构建支路电压偏差的方差模型,采用Kruskal 算法得到线路权重的最小生成树,实现对配电网拓扑运行结构的辨识;文献[20]采用DNN(深度神经网络)拟合网络导纳矩阵函数的方法得到节点间连接方式。
上述方法中,第一类馈线拓扑辨识方法以及文献[18]依赖于现有GIS 系统中的拓扑数据,不能独立地依据量测数据辨识出馈线拓扑。文献[19]依赖于μPMU 量测的相角数据,但是相角数据在普通的配电网量测设备中不可量测。第二类、第三类以及文献[20]所提方法可以独立依据量测数据辨识出馈线拓扑结构,但当馈线有补偿量未知和补偿节点未知的无功补偿时,现有辨识方法会受干扰,很难得到正确结果。
为此,本文提出了考虑馈线无功补偿的馈线拓扑辨识方法,揭示了相邻节点电压降与相邻节点间线路传输的有功和无功功率呈线性关系,进而利用线性回归辨识末端节点及其上级节点,通过迭代不断识别末端节点及其上级节点,逐渐还原馈线拓扑。算例验证了该方法的有效性和鲁棒性,表明了该方法仅需很少的数据样本即可达到较高的辨识正确率。
1 考虑无功补偿的10 kV 馈线拓扑辨识方法
1.1 馈线末端节点与其上级节点辨识方法
1.1.1 10 kV 馈线的拓扑结构
我国配电网10 kV 馈线通常挂载10~20 个专用/公用变压器(以下简称“专公变”),其拓扑呈树状结构。专公变与节点一一对应,位于馈线末端的节点称为末端节点。对于树状拓扑,每个末端节点只有唯一的上级节点。图1 所示为一个典型的10 kV 馈线拓扑结构,图中节点9,11,14,15,19 是末端节点,这些末端节点的上级节点分别是节点8,10,13,13,18。

图1 典型10 kV 馈线拓扑结构
配电网中广泛安装的量测装置记录了一条10 kV 馈线下属专公变及10 kV 馈线入端的电压幅值、有功和无功功率数据。这些数据的采样间隔通常为15 min,每天有96 个采样点。本文将节点i 对应的专公变的96 点电压、有功和无功功率数据分别称作电压曲线、有功负荷曲线和无功负荷曲线,并分别记为Pi,Qi和Ui。显然,Pi,Qi和Ui都是96 维的列向量。本节将通过这些数据辨识馈线末端节点及上级节点。
1.1.2 末端节点及其上级节点电压差与末端节点功率的线性关系
令节点j 是馈线的一个末端节点,节点i 是节点j 的上级节点,如图2 所示。

图2 末端节点j 及其上级节点i
图中:Ui和Uj是节点i 和节点j 的电压幅值;R+jX 是节点i 和节点j 间线路的阻抗;Pj和Qj是节点j 对应专公变的有功和无功功率;-Qj,[C]是节点j 处的无功补偿功率(因电容器向馈线注入无功功率,故为负)。显然,节点i 和节点j 间线路传输功率为P[T]+jQ[T]=Pj+j(Qj-Qj,[C])。令节点j的电压相角为0,则有如下电压关系:
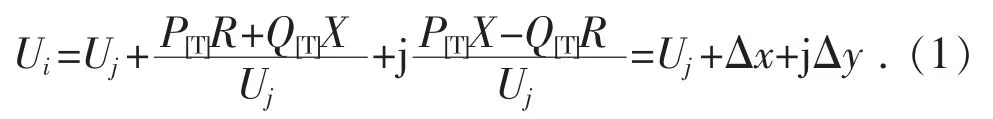
由此知电压幅值差为:

由于Δx 和Δy 很小,故可忽略高次项Δx2+Δy2,从而有
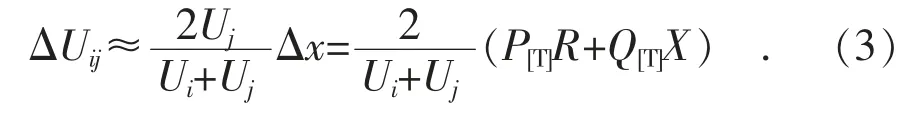
令(Ui+Uj)/2=并 将P[T]=Pj,Q[T]=Qj-Qj,[C]代入式(3),则有:

本文采用最小二乘法求解式(4)的线性回归模型,并采用SSE(误差平方和)评价线性回归模型的拟合程度。SSE 定义如下:

式中:yi为采样值;为线性回归值;n 为采样数据点的数量。SSE 越小,线性回归模型拟合越好。
1.1.3 末端节点及其上级节点的辨识方法
由于只有末端节点和上级节点的组合存在式(4)的线性关系,故在所有的节点组合中,选取最小的SSE,即可筛选出末端节点及上级节点组合。基于Pi,Qi,Ui数据辨识馈线末端节点及其上级节点的具体步骤如下:
(1)输入节点数m,节点编号集合{1,2,…,m},节点的有功(P1,P2,…,Pm)、无功(Q1,Q2,…,Qm)以及电压(U1,U2,…,Um)数据。
(2)从节点编号集合中取出2 个节点编号进行排列,所有排列的可能性组成集合S[A]。
(3)取出集合S[A]的一个元素(i,j),利用数据Pj,Qj,Ui,Uj求解式(4)的线性回归模型,计算其SSEi,j,并将SSEi,j记录在集合S[SSE]中。
(4)遍历集合S[A],对每一个元素都执行步骤(3)的操作。
(5)取集合S[SSE]中最小值对应的集合S[A]中的元素(p,q),则节点q 是一个末端节点,节点p是节点q 的上级节点。
辨识末端节点及其上级节点流程如图3 所示。
1.2 10 kV 馈线拓扑的辨识方法
在输入数据中辨识出末端节点后,即可剔除末端节点,并将其功率加至其上级节点,从而修改后的数据仍可继续执行1.1 节的末端节点辨识操作。以图1 所示的10 kV 馈线为例,由式(4)可知,节点9 和节点8 以及节点8 和节点7 的量测数据近似满足如下线性回归模型。
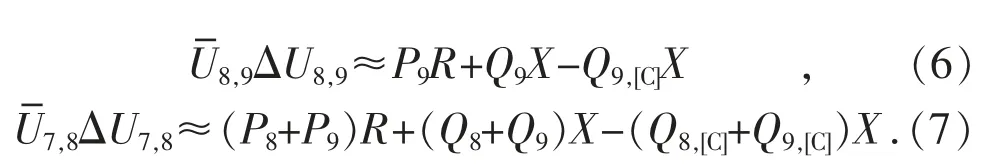
假设第一次辨识末端节点操作后,节点9 辨识为末端节点,节点8 为其上级节点。在剔除节点9,并将节点9 的有功和无功数据加到节点8上后,再执行辨识末端节点操作,因存在式(7)的线性关系,节点8 和节点7 即可辨识为新的末端节点及其上级节点。
显然,不断重复辨识末端节点、剔除末端节点、将末端节点的功率加到其上级节点这三步操作,就能逐步辨识出馈线的拓扑结构,具体步骤如下:
(1)输入节点编号集合{1,2,…,m},节点数m,节点的有功(P1,P2,…,Pm)、无功(Q1,Q2,…,Qm)以及电压(U1,U2,…,Um)数据。
(2)采用1.1 节的末端节点及其上级节点辨识方法,辨识出一对末端节点及上级节点组合(p,q),并将其记录在集合S[T]中。
(3)在节点编号集合中删除节点q,并令节点数m=m-1;再令Pp=Pp+Pq,Qp=Qp+Qq,并删 除Pq和Qq;最后,删除Uq。
(4)若m>1,返回步骤1;若m=1,根据集合S[T]中末端节点及其上级节点的组合还原馈线拓扑。
10 kV 馈线拓扑的辨识方法流程如图4 所示。

图4 10 kV 馈线拓扑的辨识方法流程
需说明的是,将解线性回归模型得到的常数项-Qj,[C]X 除以无功功率前面的系数X,可得到Qj,[C]。当节点j 不是馈线的末端节点时,Qj,[C]的意义发生了变化。由式(6)和式(7)不难看出,Qj,[C]是节点j 及其所有下属节点的无功补偿功率之和,故在本文中将Qj,[C]称为节点j 的累计无功补偿功率。
本文所提拓扑辨识方法也适用于电缆馈线的拓扑辨识。由于电缆的充电功率较大,难以忽略,且其大小又很难估计,故传统方法辨识电缆馈线拓扑的准确率较低。对本文方法,由于电缆的充电功率可视为相关各节点的一个大小未知的无功补偿,故完全适用于本文的拓扑辨识机理。
2 算例
2.1 算例说明
为了更好地测试所提方法的性能,以IEEE 18 节点和IEEE 33 节点系统为基础,构造图5 和图6 所示的两个10kV 馈线系统。其中两系统的节点1 均为电源点,对应于平衡节点,其余节点均为专公变,对应于PQ 节点。为了保证负荷曲线的真实性,选取某地区专公变的有功量测数据Pi和无功量测数据Qi,将其设置为两构造系统PQ节点的有功和无功负荷。设平衡节点的负荷为0,电压始终保持为1,则可通过96 次潮流计算,获得每个PQ 节点的电压曲线Ui。

图5 IEEE 18 节点系统拓扑

图6 IEEE 33 节点系统拓扑
两系统各PQ 节点的有功和无功曲线如图7所示,其中各节点有功功率均值为0.294 7 MW,无功功率均值为0.109 2 Mvar。
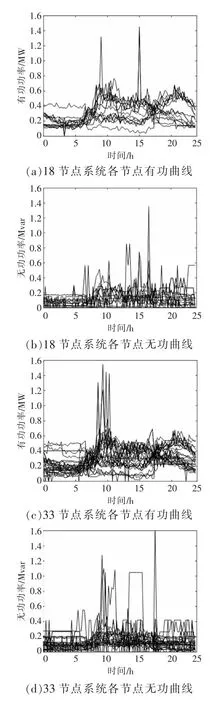
图7 各PQ 节点的有功、无功数据
考虑有、无无功补偿两种情况,其中有无功补偿时,补偿大小如图5 和图6 所示。表1 和表2 比较了两系统有、无无功补偿时各节点电压的均值。可见,无功补偿显著提升了末端节点电压,将其控制在0.95 p.u.以上,其影响不可忽略。
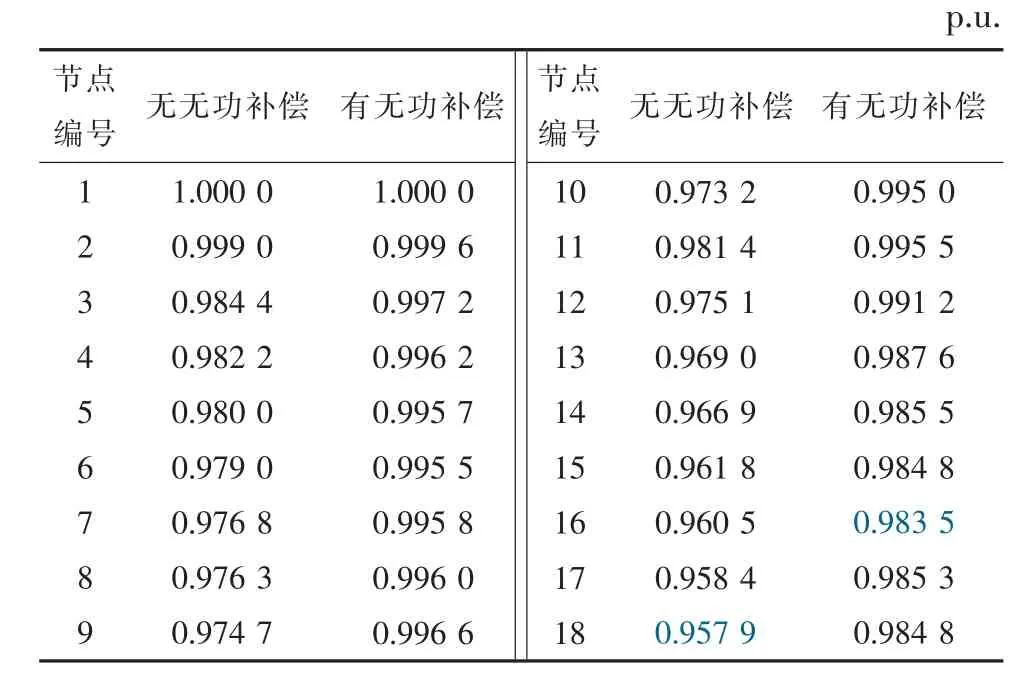
表1 IEEE 18 节点系统各节点平均电压
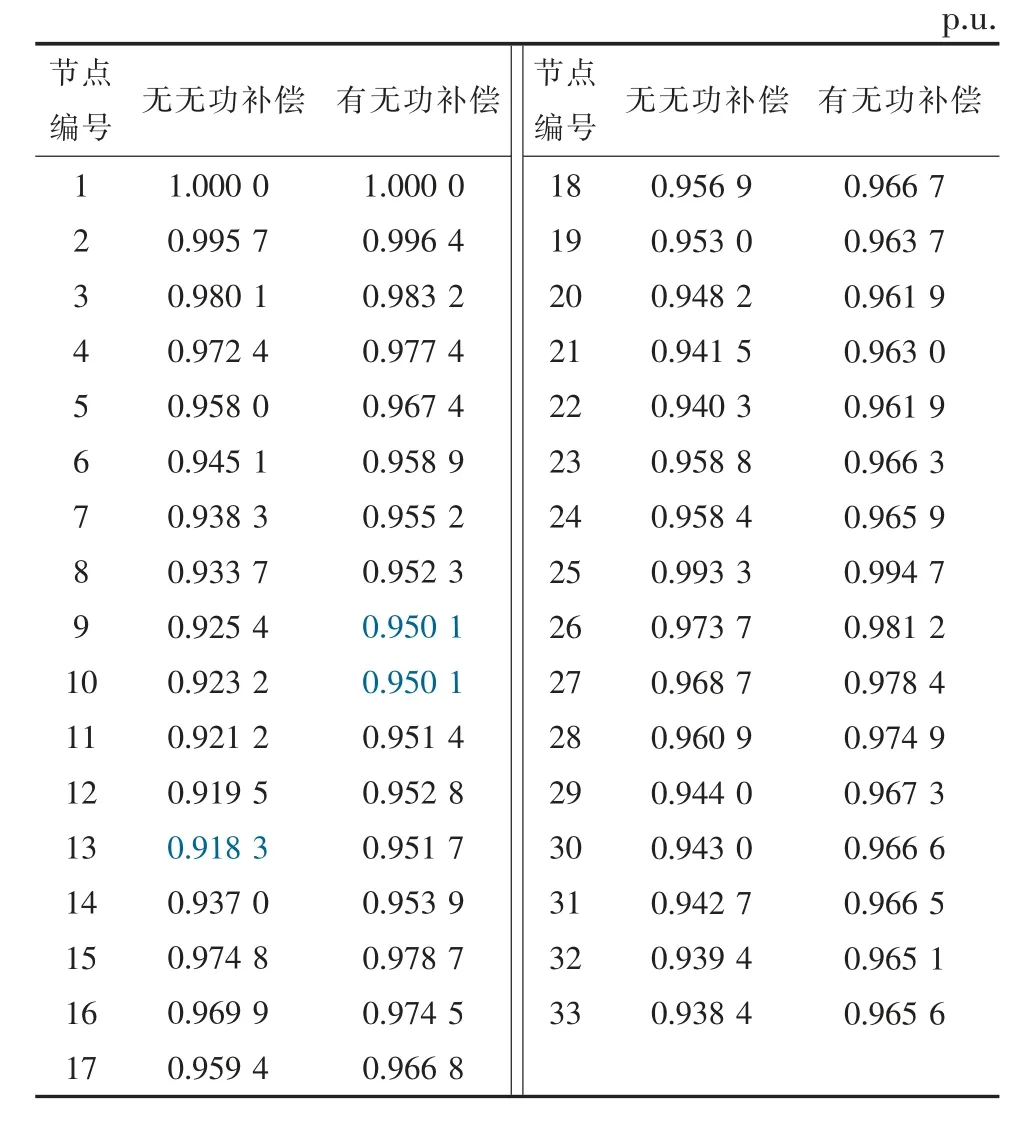
表2 IEEE 33 节点系统各节点平均电压
2.2 10 kV 馈线拓扑辨识
基于2.1 节考虑无功补偿情况下各节点的Pi,Qi及Ui数据,采用1.2 节的方法辨识馈线拓扑。算法迭代辨识过程如表3 及表4 所示,由表可见,每次迭代都获得了馈线拓扑中存在的支路,均未将不存在线路连接的两节点指定为末端及其上级节点。由表3 和表4 的迭代辨识过程即能重构馈线拓扑,可验证,重构拓扑与图5 和图6 所示的相同。
两系统拓扑辨识历次迭代过程中的SSE 分别如图8 和图9 所示,图中每一列×标记与○标记都代表某一次迭代中所有节点组合的SSE,其中×标记代表末端节点组合及其上级节点组合的SSE,○标记代表其他节点组合的SSE。

表3 IEEE 18 节点系统迭代辨识过程

表4 IEEE 33 节点系统迭代辨识过程
2.2.1 系统拓扑辨识结果分析
由图8 和图9 可知:
(1)每次迭代的×标记有多个,对应不同的末端节点及其上级节点组合。随着迭代的进行,末端节点数和拓扑分支数减少,×标记的数量也在不断减少。因每次迭代均去除最小SSE 对应的末端节点,故虚线上的×标记对应的末端节点即是被去除的末端节点。
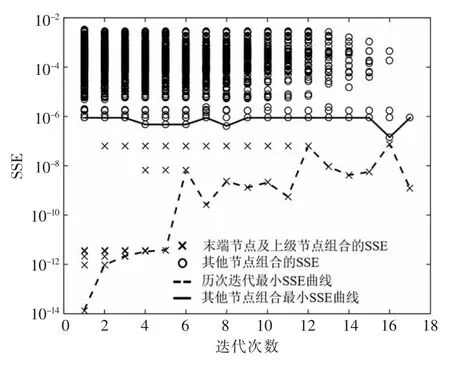
图8 18 节点系统历次迭代过程中的SSE

图9 33 节点系统历次迭代过程中的SSE
(2)末端节点及上级节点组合的SSE 显著小于其他节点组合。这验证了式(4)线性关系的合理性,也保证了拓扑辨识的正确性。
(3)历次迭代被去除的末端节点的SSE(即虚线上的×标记)随着迭代的进行逐渐增大,原因是随着迭代的进行,末端节点与上级节点间线路传输的功率增大,导致式(2)中高次项逐渐不可忽略,式(4)的线性程度降低,SSE 增大。
(4)随着辨识节点数的增多,可能会出现由于节点数过多,线路传输功率增大,导致线性程度降低,进而影响辨识正确性的情况。因33 节点系统在辨识结束时SSE 仍显著小于其他节点组合的SSE,故可推测,该方法应用于普遍小于20个节点的实际系统时,不会因线性程度降低而导致辨识错误。
2.2.2 系统无功补偿位置分析
通过分析各节点累计充电功率Qj,[C]可知无功补偿位置。两系统辨识过程中各节点的累计充电功率如图10 所示。由图可见:
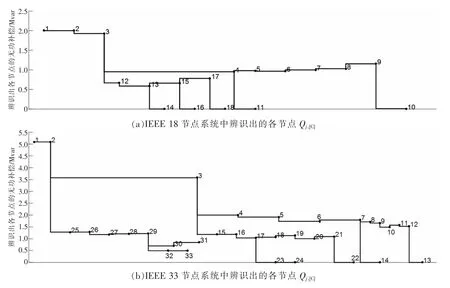
图10 两系统辨识出的各节点的Qj,[C]
(1)对末端节点,其累计无功补偿功率即是该节点的无功补偿功率。因此,若末端节点的累计无功补偿功率显著大于0,那么该末端节点有无功补偿,如33 节点系统的节点31,33;若末端节点的累计无功补偿功率接近于0,那么该末端节点无无功补偿,如18 节点系统的节点10,11,14,16,18 和33 节点系统的节点13,14,22,24。
(2)对非末端节点,若其累计无功补偿功率与其下级节点的累计无功补偿功率相比存在一个较大的跳跃,说明该节点存在无功补偿,如18节点系统的节点9,17 和33 节点系统的节点12,21。
(3)对存在多个下级节点的非末端节点,由于其累计无功补偿功率近似为所有下级节点累计无功补偿功率之和,故也存在跳跃。如18 节点系统的节点3,4,13,15 和33 节点系统的节点2,3,7,17,29。但这不是由该节点的无功补偿引起的,故这些节点不存在无功补偿。
基于上述分析,可知18 节点系统的节点9,17 有无功补偿,33 节点系统的节点31,33,12,21 有无功补偿,这与图5 和图6 所示的补偿位置完全相同。
2.3 鲁棒性分析
为分析所提方法正确率与功率误差的关系,将两系统输入算法的Pi和Qi加入不同大小随机误差,Ui保持不变。此时辨识正确率与误差的大小关系如图11 所示。由图11 可见,当功率误差在10%以内时,两系统的辨识正确率均为100%;当在功率误差在10%~20%之间时,辨识正确率显著下降;当功率误差超过20%时,辨识正确率降为0。
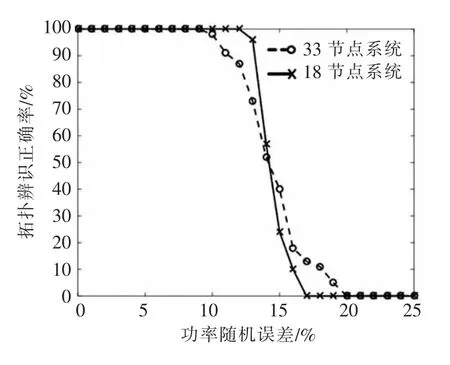
图11 辨识正确率与功率误差的关系
为分析辨识正确率与电压误差之间的关系,认为每个表计的电压量测都有特定大小的固定误差,不同表计的固定误差呈均值为0 的正态分布。对两系统的电压数据加入误差后,辨识正确率与正态分布方差δ 的关系如图12 所示。图12显示,33 节点系统的辨识准确率随δ 增大而减小的速度略大于18 节点系统,当δ 为0.001,即66.4%的节点电压固定误差在0.001 p.u.以内时,两系统的拓扑辨识正确率均在90%以上。
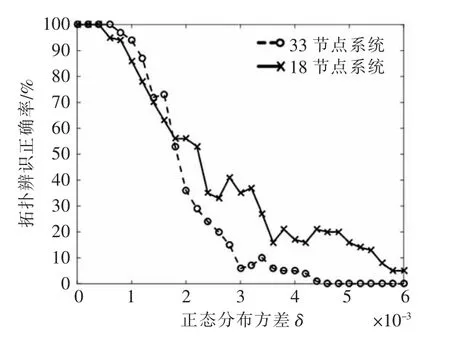
图12 辨识正确率与误差正态分布方差的关系
显然,拓扑辨识的准确率对电压误差的敏感性显著大于对功率误差的敏感性,这是因为10 kV 馈线各节点电压均接近于额定电压,因此相邻节点电压差很小,而辨识算法依赖于相邻节点的电压差,故辨识正确率对电压误差更敏感。
2.4 辨识耗时分析
10 kV 馈线节点数是影响拓扑辨识耗时的主要因素。由于算法每次迭代减少一个节点,即将一个n+1 节点系统变为n 节点系统,因此每次迭代消耗的时间即是n+1 节点系统与n 节点系统拓扑辨识消耗时间之差。通过记录每次迭代所消耗的时间,并将后n 次迭代消耗的时间相加,可得n+1 节点系统拓扑辨识消耗时间,如图13 所示。18 节点系统和33 节点系统拓扑辨识耗时分别为1.6 s 和10.1 s。经多项式拟合,可知拓扑辨识消耗的时间t 与节点数n 的三次方成正比,拟合结果为t≈3.025×10-4n3。

图13 拓扑辨识耗时与节点个数的关系
2.5 辨识正确率与数据样本数量的关系
线性回归输入的数据样本数量会影响拓扑辨识正确率。辨识正确率与数据样本数量的关系如表5 所示。表5 显示,仅需6 个及以上的数据样本,即可达到100%的辨识正确率。需说明的是,实验显示,拓扑辨识消耗时间与数据样本数量几乎没有关系。
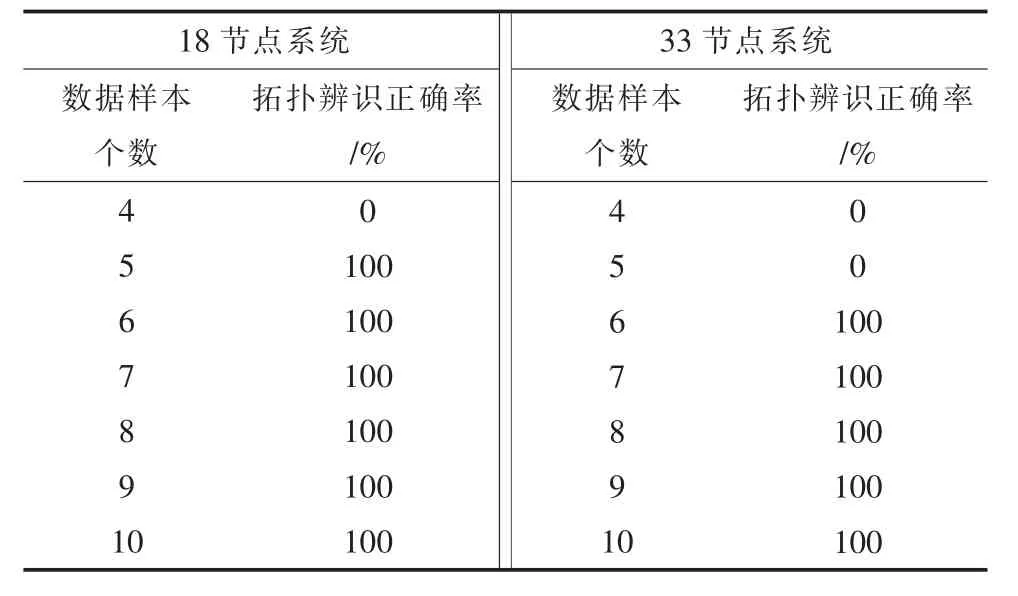
表5 辨识正确率与数据样本数量的关系
3 结语
本文针对考虑无功补偿的10 kV 馈线拓扑辨识问题,基于配电网量测装置采集的节点电压、有功和无功负荷功率三者的稳态测量数据,提出了一种数据驱动的辨识方法。理论分析表明,该方法不仅可应用于有无功补偿的馈线,还可应用于充电功率较大的电缆馈线。算例分析表明,该方法仅需很少的数据样本即可准确地辨识,并对功率量测具有较好的鲁棒性,此外,还能正确辨识出无功补偿所在节点位置。
