基于Copula函数的土石坝三维坝坡稳定可靠度分析
2021-02-24宋来福,孔宪京,徐斌,庞锐
宋 来 福,孔 宪 京,徐 斌,庞 锐
( 大连理工大学 水利工程学院, 辽宁 大连 116024 )
0 引 言
土石坝工程的安全性一直是坝工界关注的焦点,其中,坝坡稳定性是影响土石坝工程安全的主要问题之一[1].在土石坝建设过程中存在大量的不确定性[2-4],现有确定性分析方法无法解决对其不确定性认知的局限性.可靠度理论可以合理、系统地对各种不确定性进行定量分析,使岩土工程结构物设计、分析符合工程实际,近年来在边坡稳定分析领域受到高度重视并得到广泛应用[5-7].目前,定量表征不确定性及减小不确定性的方法已成为岩土边坡包括土石坝坝坡稳定可靠度分析的研究热点.
岩土物理力学参数的不确定性是岩土工程不确定性的主要来源,合理表征岩土体参数的不确定性是岩土工程可靠度分析的关键.堆石料作为主要的筑坝材料,其非线性强度参数是影响土石坝坝坡稳定的关键指标[8-12].因此,学术界将非线性强度参数作为随机变量对土石坝坝坡稳定可靠度进行了大量研究[13-16].然而,目前的研究忽略了非线性强度参数间的相关性,将其作为独立的随机变量.大量试验研究表明[17-21]:筑坝堆石料非线性强度参数间存在显著的正相关性.因此,在土石坝坝坡稳定可靠度分析过程中,忽略了非线性强度参数间的相关性显然是不合理的,应充分考虑非线性强度参数间的相关性,建立符合非线性强度参数分布特征的联合概率分布模型(下文简称联合分布模型),即获取完备概率信息.但受经济、技术等条件的限制,土石坝工程试验数据有限,样本数量无法达到统计要求,仅可获得非线性强度参数的边缘分布函数与相关系数,即不完备概率信息.在不完备概率信息条件下,无法确定合理的非线性强度参数联合分布函数.Copula函数为不完备概率信息条件下构造非线性强度参数联合分布函数提供了一种简单有效的途径,在岩土工程可靠度分析领域得到广泛应用[22-27],如Tang等[28]和Li等[29]采用Copula函数对岩土结构系统的可靠度进行了研究;Xu等[30]基于Copula理论对地震边坡进行了三维可靠度分析;Pan等[31]基于Copula函数建立了隧道工程钻进工作面可靠度分析模型.目前,尚未见到关于筑坝堆石料非线性强度参数联合分布模型研究,鉴于Copula函数在建立岩土体参数联合分布模型方面的显著优势,有必要采用Copula函数对筑坝堆石料非线性强度参数联合分布模型进行研究,为准确评估土石坝坝坡稳定可靠度提供可靠的模型、数据支持,对于探索土石坝坝坡稳定可靠度分析具有重要的意义.
因此,本文在考虑堆石料非线性强度参数不完备概率信息条件下,采用Copula函数建立非线性强度参数联合分布模型,结合径向基神经网络(radial basis function network,RBFN)提出土石坝坝坡稳定系统可靠度分析智能响应面法,并通过与传统独立正态分布模型算例结果进行比较,分析基于Copula函数建立非线性强度参数联合分布模型开展土石坝坝坡稳定系统可靠度分析的必要性.最后,系统研究Copula函数类型与样本数量对土石坝坝坡稳定系统可靠度的影响规律.
1 基于Copula函数建立非线性强度参数联合分布模型
Copula理论[32]认为可以根据N个边缘分布函数和相关结构精确地建立N维联合分布函数模型.基于二维分布,Copula函数定义为[0,1]2空间中边缘分布为区间[0,1]的均匀分布[33],由Sklar定理[32],非线性强度参数φ0和Δφ的联合分布函数为
F(φ0,Δφ)=C(F1(φ0),F2(Δφ);θ)=C(u1,u2;θ)
(1)
式中:u1=F1(φ0)、u2=F2(Δφ)分别为非线性强度参数φ0和Δφ的边缘分布函数,θ为Copula 函数的参数.
非线性强度参数φ0和Δφ的联合概率密度函数为
f(φ0,Δφ)=f1(φ0)f2(Δφ)D(F1(φ0),F2(Δφ);θ)
(2)
式中:f1(φ0)、f2(Δφ)分别为非线性强度参数φ0和Δφ的边缘概率密度函数,D(F1(φ0),F2(Δφ);θ)为Copula函数的密度函数.
当已知Copula函数、非线性强度参数的边缘分布函数和边缘概率密度函数及Copula函数的参数,由式(1)、(2)便可求出非线性强度参数的联合分布函数和联合概率密度函数.
Copula函数的参数θ可由Kendall秩相关系数或Pearson线性相关系数求得[33].Kendall秩相关系数R的表达式为
(3)
Copula函数的参数为
(4)
2 三维边坡稳定分析
二维边坡稳定分析方法概念明确、理论成熟、计算方便、应用广泛.然而,在实际工程中边坡失稳破坏均呈三维状态,三维边坡稳定分析能真实反映边坡宽度、边界条件等影响,可直接用于三维边坡坡面三量分布规律的研究.对于土石坝工程,宽河谷、低坝应用二维分析计算简便、保守安全.然而,随着施工技术的进步,土石坝坝体形状逐步向更窄、更高的方向发展,河谷三维效应明显,二维简化分析可能会造成分析结果不够准确[34-36].为避免二维模型分析存在的不足,真实反映土石坝的形状分布,获得更符合实际状态的分析成果,开展三维边坡稳定分析是十分必要的.
因此,本文在课题组开发的有限元分析软件GEODYNA基础上,开发了三维边坡稳定程序并进行了算例验证,为深入开展土石坝三维坝坡动力稳定可靠度研究提供有效的技术手段.
本文通过有限元分析得到单元应力的各个分量,得到滑动面上点的应力分量,再由滑动面上的应力分量,求得滑动面上的法向与切向应力.
一般空间问题包含6个应力分量、6个变形分量和3个位移分量,且均为x、y、z坐标变量函数.已知任意一点P的应力分量σx、σy、σz、τxy=τyx、τxz=τzx、τyz=τzy,斜面上任意一点P附近取一个平面ABC,过点P与平行于坐标面的3个平面形成一个微小四面体PABC,如图1所示,当四面体PABC无限减小而趋于点P时,平面ABC上的应力为该斜面上的应力.
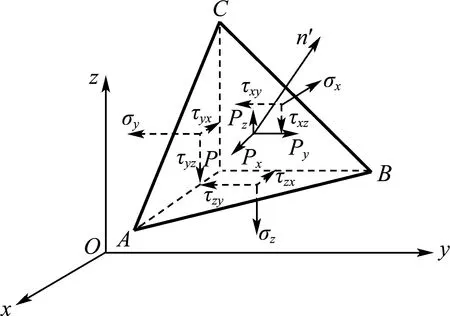
图1 四面体PABC的应力状态
假设平面ABC外法线n′的方向余弦为cos(n′,x)=l,cos(n′,y)=m,cos(n′,z)=n.根据四面体的平衡条件∑Fx=0,∑Fy=0,∑Fz=0,可得:
FP,x=lσx+mτyx+nτzx
FP,y=mσy+nτzy+lτxy
FP,z=nσz+lτxz+mτyz
平面ABC的法向应力σ和切向应力τ分别为
σ=l2σx+m2σy+n2σz+2mnτyz+2nlτzx+2lmτxy
由此可知任意斜面上安全系数的表达式为
式中:ci、φi分别为第i个单元体的黏聚力和内摩擦角;Si为滑弧穿过第i个单元的面积;σi、τi分别为第i个单元滑弧面上的法向和切向应力;N为求和数量.
滑动面搜索采用枚举法,即通过规定的球心空间范围和椭球体长短轴半径进行搜索,按规定顺序逐次进行计算,在所有滑动面中选取安全系数最小值为该边坡的安全系数最小值.详细的分析方法及验证过程见文献[37].
3 基于Copula函数的土石坝三维坝坡稳定系统可靠度分析
3.1 土石坝三维坝坡稳定系统可靠度定义
土石坝坡体内可能存在大量潜在滑动面,坝坡可沿坡体内任意滑动面滑动.因此,可将土石坝坝坡稳定问题定义为一个由大量潜在滑动面构成的串联系统可靠度问题.串联系统整体失效概率Pf可以表示为
Pf≈P(E(Fs1(X)<1))∪P(E(Fs2(X)<1))∪…∪P(E(FsM(X)<1))
(5)
式中:P(·)为边坡失效事件的发生概率,Fsi(X)为坝坡沿滑动面i发生失稳破坏的安全系数,E(Fsi(X)<1)为坝坡沿滑动面i发生失稳破坏的事件,M为计算的坝坡失稳破坏的滑动面数量.土石坝坝坡稳定系统失效概率的表达式为
(6)
式中:X={x1,x2,…,xD}为影响坝坡稳定的随机变量,D为随机变量的数量;g(X)=Fs(X)-1.0,为功能函数,Fs(X)为用确定性坝坡稳定分析方法解得的安全系数;fx(X)为联合概率密度函数.但是,联合概率密度函数求解十分困难,只可近似求解,计算结果存在较大的误差.因此,工程中多采用Monte-Carlo法(MCS),其基本表达式为
(7)
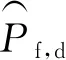
3.2 土石坝三维坝坡稳定系统可靠度分析智能响应面法
Monte-Carlo法(MCS)概念清晰、明确,但需要进行大量的确定性计算,时间成本高、效率低.为了提高计算效率、保证计算精度,本文提出了土石坝坝坡稳定系统可靠度分析的智能响应面法.该方法适应能力强,容错性高,且具有更大灵活性和强非线性的拟合方法,计算精度高,并在二维边坡可靠度分析中得到了很好的验证、应用[38-41].
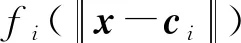
(8)
式中:A为径向基函数的扩展常数,反映了函数图像的宽度.
RBFN选定单元j的最终输出可以表示为
(9)
其中wjh为输出层的权重.
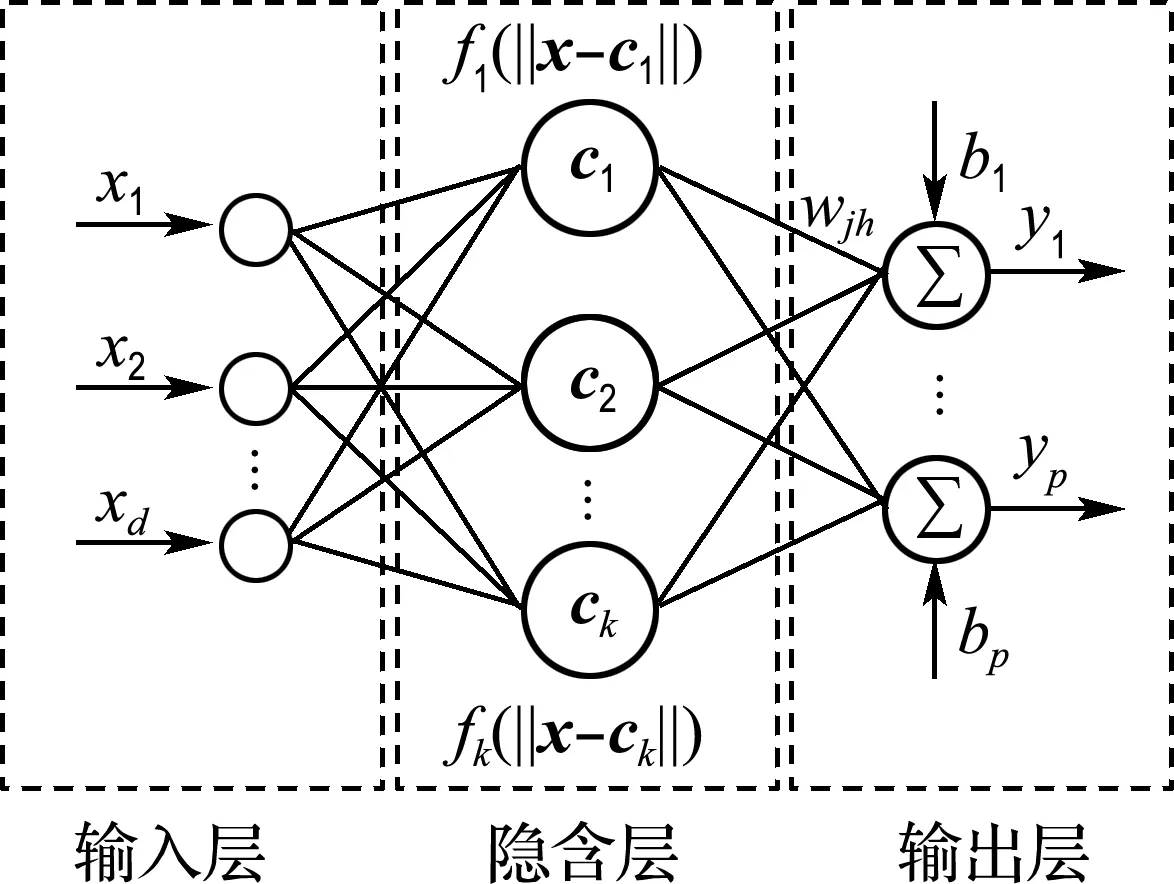
图2 RBFN结构
3.3 基于Copula函数的土石坝三维坝坡稳定系统可靠度分析框架
本文借助MATLAB程序,基于Copula函数与智能响应面法计算土石坝三维坝坡稳定系统失效概率.主要分为3个步骤:(1)建立符合原始数据分布特征的联合分布模型;(2)确定坝坡稳定系统可靠度分析的智能响应面;(3)进行土石坝三维坝坡稳定系统可靠度分析.具体的分析流程如图3所示.
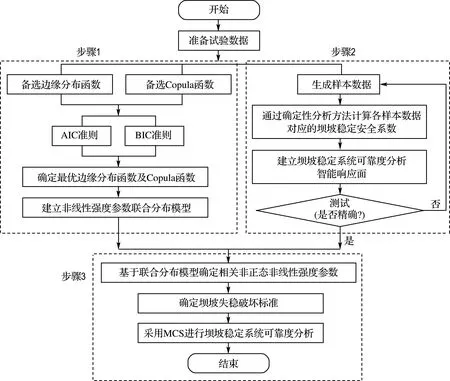
图3 土石坝三维坝坡稳定系统可靠度分析流程
4 算例分析
4.1 计算模型
本文将面板堆石坝作为分析对象,建立了高度为200 m的计算模型.坝顶宽16 m,上、下游坝坡系数分别为1.4、1.6,面板厚度为0.3+0.003 5H(H为坝高),大坝分层填筑,蓄水高度为175 m,下游无水.面板和堆石料间设置接触面单元.
计算模型共计80 573个节点,75 980个单元,包括坝体、两侧山体及基岩,在基岩底部及四周山体施加约束,分析静力荷载作用下土石坝三维坝坡稳定性,有限元模型如图4所示.
4.2 建立堆石料非线性强度参数数据库
足够的样本数量是进行数据统计分析的基础,土石坝工程多为小样本数据,无法达到统计要求.为准确表征堆石料非线性强度参数的概率分布类型与相关性特征,本文参考类似工程的试验资料,详细汇总了国内外124座土石坝工程相关信息,得到767组堆石料非线性强度参数数据(如图5所示),为建立准确的堆石料非线性强度参数联合分布模型提供重要的数据支持.因试样及试验误差等众多因素的影响,统计的数据中可能存在异常点,本文选用3σ法则对异常点进行剔除,得到755组有效数据.其他材料参数如表1所示.
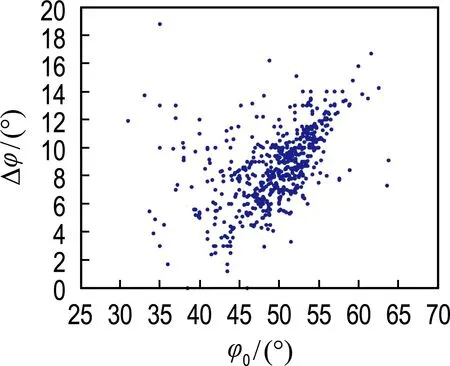
图5 堆石料非线性强度参数数据

表1 材料参数
4.3 建立堆石料非线性强度参数联合分布模型
4.3.1 最优边缘分布函数 为了能够合理且全面地涵盖堆石料非线性强度参数的最优概率分布类型,本文选取表2所示5种边缘分布函数,结合AIC[42]与BIC[43]准则确定最优边缘分布函数.结果如表3所示,由表可知,堆石料非线性强度参数φ0、Δφ最优边缘分布类型分别为威布尔分布与截尾正态分布.图6给出了基于原始数据拟合的5种不同边缘分布概率密度曲线,显然,最优分布函数类型能够更好地拟合数据的分布特征,结果与表3一致.
4.3.2 最优Copula函数 数学上有多种Copula函数,鉴于堆石料非线性强度参数间存在显著的正相关性,因此,本文选择能够很好表征正相关性的8种Copula函数(如表4所示),采用AIC与BIC准则确定最优Copula函数,结果如表5所示,由表可知,最优Copula函数是Plackett Copula函数.图7展示了原始数据二维频率直方图与二维Plackett Copula函数概率密度函数图,显然,图7(a)与(b)具有相似的分布形状,说明Plackett Copula函数能够准确地描述堆石料非线性强度参数间的相关性.

表2 5种备选边缘分布函数

表3 最优边缘分布函数识别结果

表4 8种Copula函数
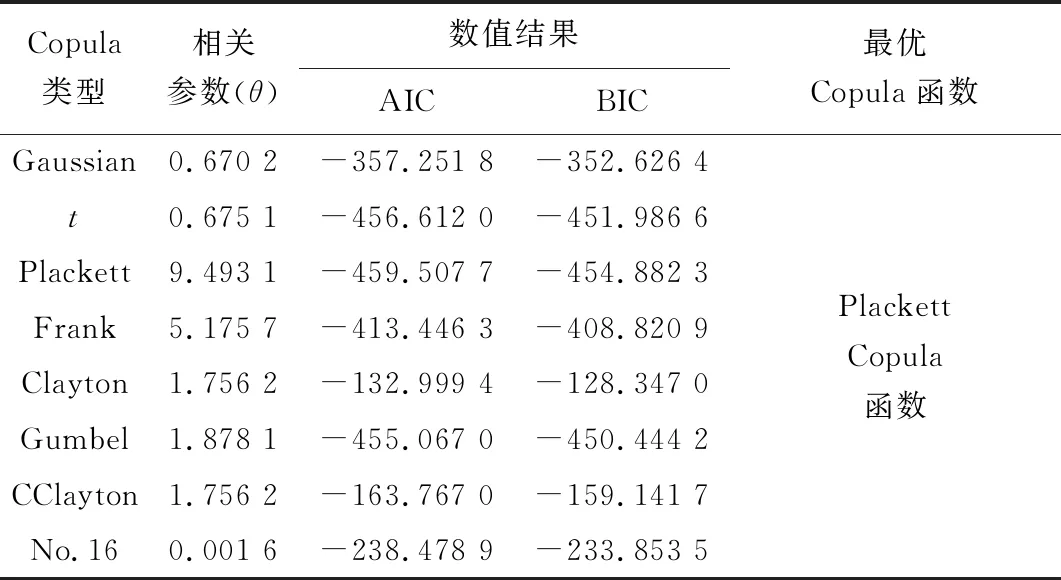
表5 最优Copula函数识别
4.3.3 堆石料非线性强度参数仿真数据模拟 确定最优边缘分布函数与Copula函数之后,由式(1)可得堆石料非线性强度参数联合分布函数.联合分布函数的主要作用是模拟符合堆石料分布特征的仿真数据,为土石坝坝坡稳定可靠度分析提供可靠的具有统计意义的参数样本.图8分别展示了传统独立正态分布模型与最优Copula函数(Plackett Copula函数)构造的联合分布模型模拟的30 000组仿真数据.显然,传统独立正态分布模型仿真数据呈离散均匀分布,无法考虑变量间的边缘分布与相关性.Plackett Copula函数能够较准确地拟合实测数据的分布特征,验证了表5结果的准确性.
4.4 结果分析
图9给出了不同安全系数下,传统独立正态分布与最优Copula函数建立的联合分布模型计算的土石坝三维坝坡失效概率.由图可知,传统独立正态分布模型忽略了非线性强度参数的相关性,计算的失效概率过小,高估了土石坝坝坡稳定系统的可靠度.
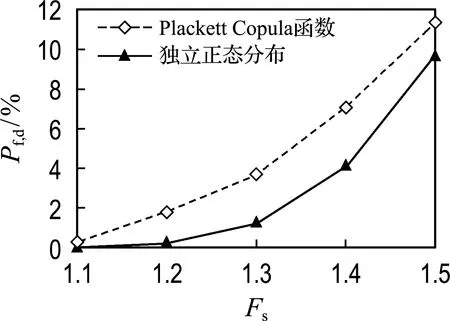
图9 不同分布模型的坝坡系统失效概率
因此,在进行土石坝三维坝坡稳定系统可靠度分析时,应充分考虑非线性强度参数的相关性,基于Copula函数合理描述样本数据的边缘分布与相关结构,为准确评估土石坝坝坡稳定系统可靠度提供模型、数据支持.
5 结果讨论
不同的Copula函数具有不同的结构类型,对坝坡稳定系统失效概率有显著的影响.因此,合理选择Copula函数是分析坝坡稳定系统可靠度的重要环节.同时,岩土工程中多为小样本数据,样本数量可能对参数的相关性等产生影响.因此,本文从Copula函数类型与样本数量两个方面对土石坝三维坝坡稳定系统可靠度的影响进行讨论.
5.1 Copula函数类型对土石坝坝坡稳定系统可靠度的影响
Plackett Copula函数是拟合堆石料非线性强度参数的最优Copula函数.因此,将Plackett Copula函数作为分析标准,表6列出了不同分布模型计算的失效概率相对误差.由表可知,不同Copula函数计算的失效概率具有明显的差异,Frank Copula函数的相对误差最小,tCopula函数的相对误差最大.相较不同Copula函数计算的结果,传统独立正态分布模型计算的失效概率误差远远大于标准值,平均相对误差达到54.1%.
5.2 样本数量对土石坝坝坡稳定系统可靠度的影响
Genest等[44]指出样本数量对参数的相关性及置信区间影响显著.因此,本文将堆石料非线性强度数据随机分成8、16、32、54、100、200、400及755组共8种不同数量的样本数据,采用表3、5中的最优边缘分布函数和Copula函数模拟30 000 组仿真数据,从模拟的非线性强度参数分布与失效概率两个方面进行讨论.
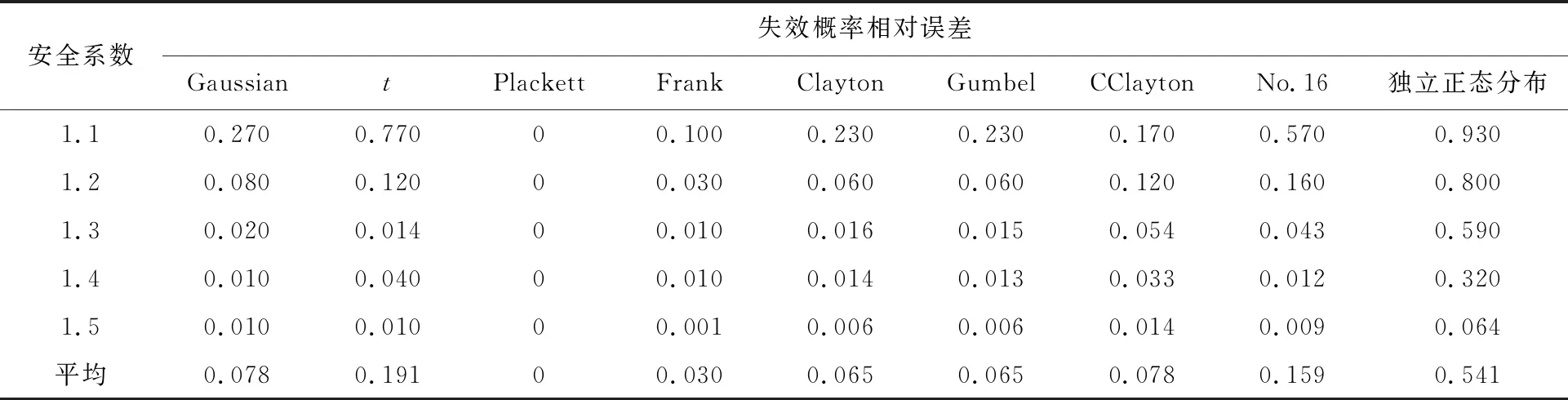
表6 不同Copula函数计算的失效概率的相对误差
图10展示了不同样本数量模拟的非线性强度仿真数据的分布情况.样本数量不同时,仿真数据形状有显著的差别,样本数量低于100时,差别尤为显著,仿真数据点更多集中分布在形状很好的区域,这是因为样本数量过少,统计特征不显著,增加了数据采样的不确定性;随着样本数量的增加,仿真数据分布形状越来越接近,最后整体趋于稳定.
表7列出了不同样本数量计算的坝坡稳定系统失效概率及相对误差(安全系数为1.3).由表可知,当样本数量低于100时,失效概率的误差达到20%以上,样本数量越少,误差越大.样本数量对于坝坡稳定系统可靠度有重要的影响,这主要体现在最优边缘分布函数与Copula函数的识别不够准确,导致三维坝坡稳定系统失效概率计算误差过大.
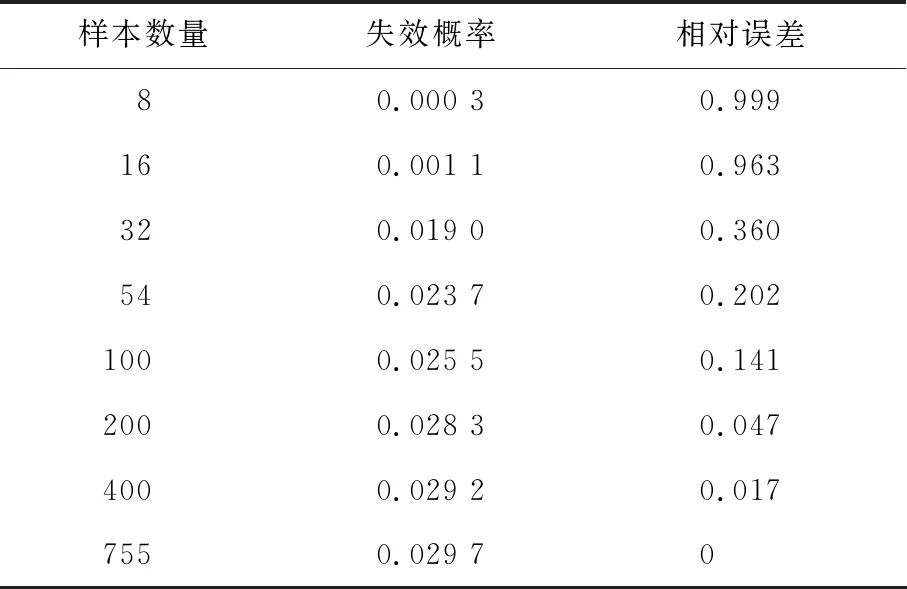
表7 不同样本数量坝坡稳定系统失效概率
6 结 论
(1)在不完备概率信息条件下,Copula函数能够合理表征堆石料非线性强度参数的相关非正态分布特征,可有效地建立堆石料非线性强度参数联合分布模型,为土石坝坝坡稳定系统可靠度分析提供可靠的具有统计意义的参数样本,对于准确评估土石坝工程安全具有重要的工程意义.
(2)传统独立正态分布模型忽略了堆石料非线性强度参数的相关非正态分布特征,计算的失效概率偏小,高估了坝坡稳定系统的可靠度.因此,在进行土石坝坝坡稳定系统可靠度分析时应充分考虑堆石料非线性强度参数间的相关非正态分布特性.
(3)Copula函数类型与样本数量对土石坝坝坡稳定系统可靠度结果有显著的影响,因此,在进行土石坝坝坡稳定系统可靠度分析时,应尽可能多地统计试验数据,选择能够表征堆石料非线性强度参数的最优Copula函数,提高坝坡稳定系统失效概率的计算精度.
