挖掘教材习题资源 提高数学解题能力

文∣张守荣

数学，需要学习者反复练习来提升熟练程度，如何做到有效练习值得我们探讨。

一、原题展现

【例】如图1，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM。下面结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有( )

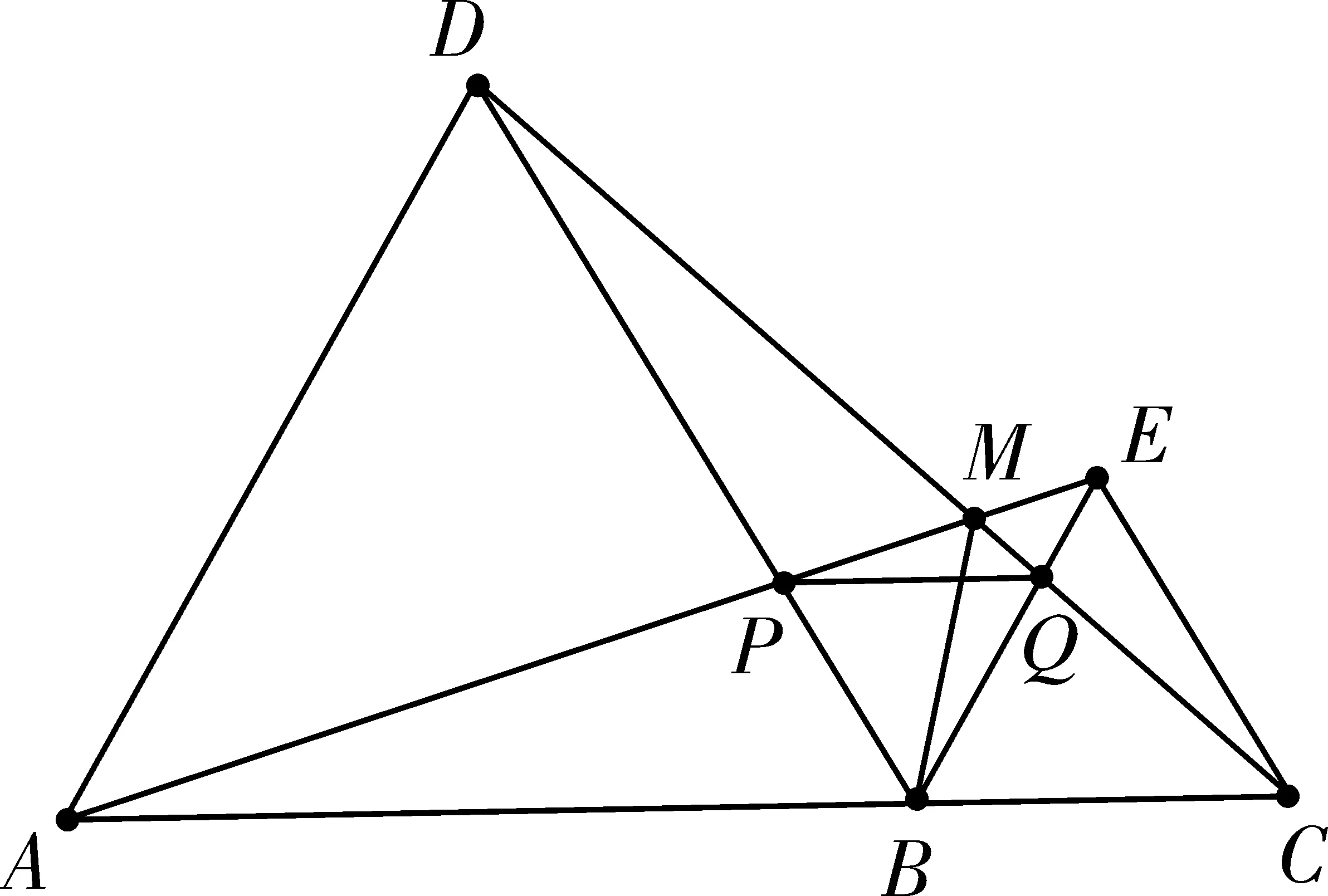
图1

A.1个 B.2个 C.3个 D.4个

这道题主要考查全等三角形的知识，以最后一道选择题呈现，是选择题中的压轴题，在学生学完全等三角形之后，教师将这道题作为最后一道选择题来测试学生学习的效果，结果几乎“全军覆没”。和学生探讨这道题失败的原因时，他们普遍认为此题“量”太大，相当于四个证明题，根本无法在短时间内完成，大家只能顺利判断第①个结论，后面几个问题能够顺利判断出来的学生越来越少，尤其第④个结论，大家根本无法判断，只能根据平时做题的“经验”。他们认为这种类型的题目很少出现所有结论都正确的情况，应该至少有一个结论是错误的，因此选择C的人数最多。学生刚学完全等三角形，虽然还没有经历初三“备考”的“刷题”历练和系统复习，对知识把握不够全面，但其根本原因还是没有认真研习教材习题，没有做到举一反三，也没有融会贯通。

简单梳理一下这四个结论的判断思路：利用“边角边”证明△ABE≌△DBC，可得出结论①；由结论①易知∠BAP=∠MDP，且∠APB=∠DPM，在△ABP和△DMP中，有两个角相等，那么剩下一个自然相等，得出∠DMA=∠ABP=60°，得出结论②；由点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，易知∠QBP=60°，要让③成立，还需证明△QBP为等腰三角形，由①知，∠BAP=∠BDQ，由△ABD为等边三角形知AB=BD，且∠DBQ=∠ABP=60°，可利用“角边角”证明△ABP≌△DBQ，得到BP=BQ，得出结论③；依据全等三角形对应边上的高相等可以得出点B到AE、CD的距离相等，即点B到∠AMC两边的距离相等，得出结论④。

二、追本溯源

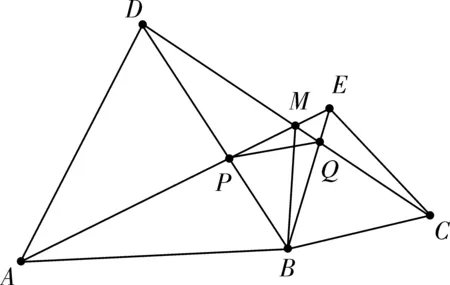
图2

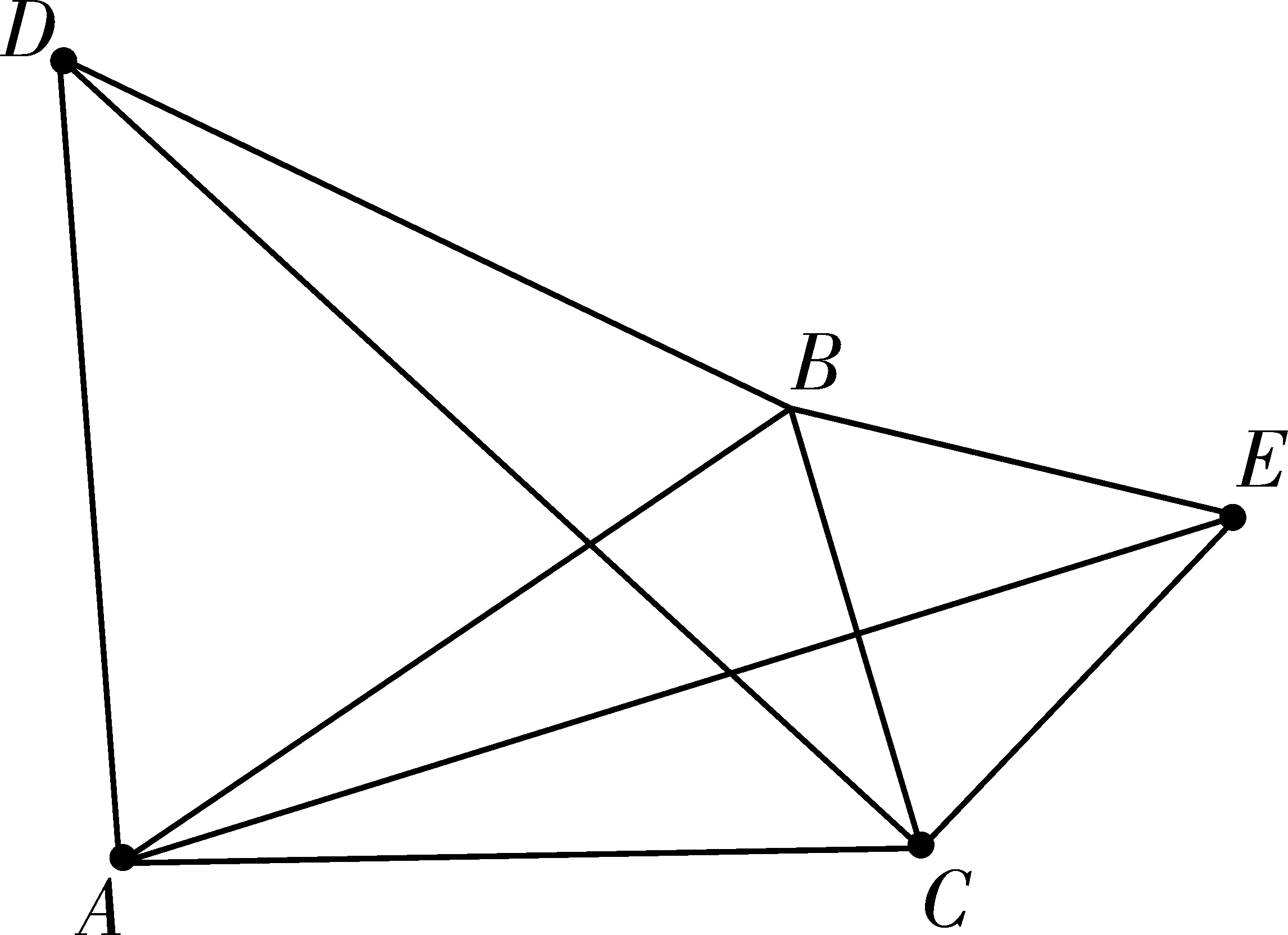
图3

教材作为教师教学和学生学习最权威的“指挥棒”，教材中的每一道例题和习题都浸透着教材专家的智慧和心血，因此，不论是教师教学，学生学习，还是考试命题，都应该充分挖掘和利用教材习题资源，以这些习题为原型展开研究和讨论。在教材中寻找结论①的“母题”，实际上排除对结论①的干扰线段MB，PQ，学生能很快判断出结论①是成立的，再“去伪存真”，学生会发现，∠DBE的大小并不影响结论①，因此对于结论①来说，点A，B，C在一条直线上可以当作伪条件来删掉，图2就作为结论①的一般图形，自然可以在图2的基础上来讨论剩下三个结论是否成立，发现等边△PBQ就“弱化”为等腰三角形，那么只有结论③不成立，其他结论都可直接由①得出，继续排除结论①的干扰“线段”，删掉线段PQ，把图2中的△BCE绕点B顺时针旋转一定的角度，并连接线段CD。就找到“母题：如图3，△ABD、△BCE都是等边三角形．求证AE=CD。(见人教版八年级上册数学第83页习题12，为了方便此文的讨论，仅字母和教材中的不一样)

三、原题再探

接着讨论这道中考选择题，表面看它考查的是全等三角形的内容，但进一步讨论发现，它的结论还可通过“圆”的知识来解决。

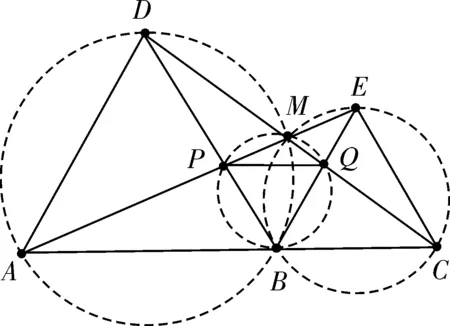
图4

如图4，先做出过点A，B，M的圆，用上述方法先证明△ABE≌△DBC后，可知∠EAB=∠CDB， 从而点D也在过点A，B，M的圆上，即点A，B，M，D四点共圆，同理可得点B，C，E，M四点也共圆，易知∠AMD=∠ABD=60°，得出结论②；根据同圆或等圆中，同弧所对圆周角相等可知∠AMB=∠ADB=60°，∠BMC=∠BEC=60°，可得出结论④；∠PMQ=∠AMB+∠BMC=120°，同时∠PBQ=60°，说明四边形PBQM的对角互补，可得出P，B，Q，M四点共圆，而PB，QB分别为∠PMB和∠QMB所对的弦，且这两个角相等，因此PB=QB，得出结论③。重温此题，发现它不仅可以用全等三角形的知识来解决，还可以用圆的知识解决，形成了知识之间的互通和共享。不仅拓宽了学生的解题思路，还发展了学生的思维。

对于喜欢探索的学生来说，还会发现三个圆“和谐”地聚在一起，想着它们一定还有“和谐”的结论，研究之后易知，如图5，三个圆的圆心在同一条直线上，且这条直线为线段BM的垂直平分线。

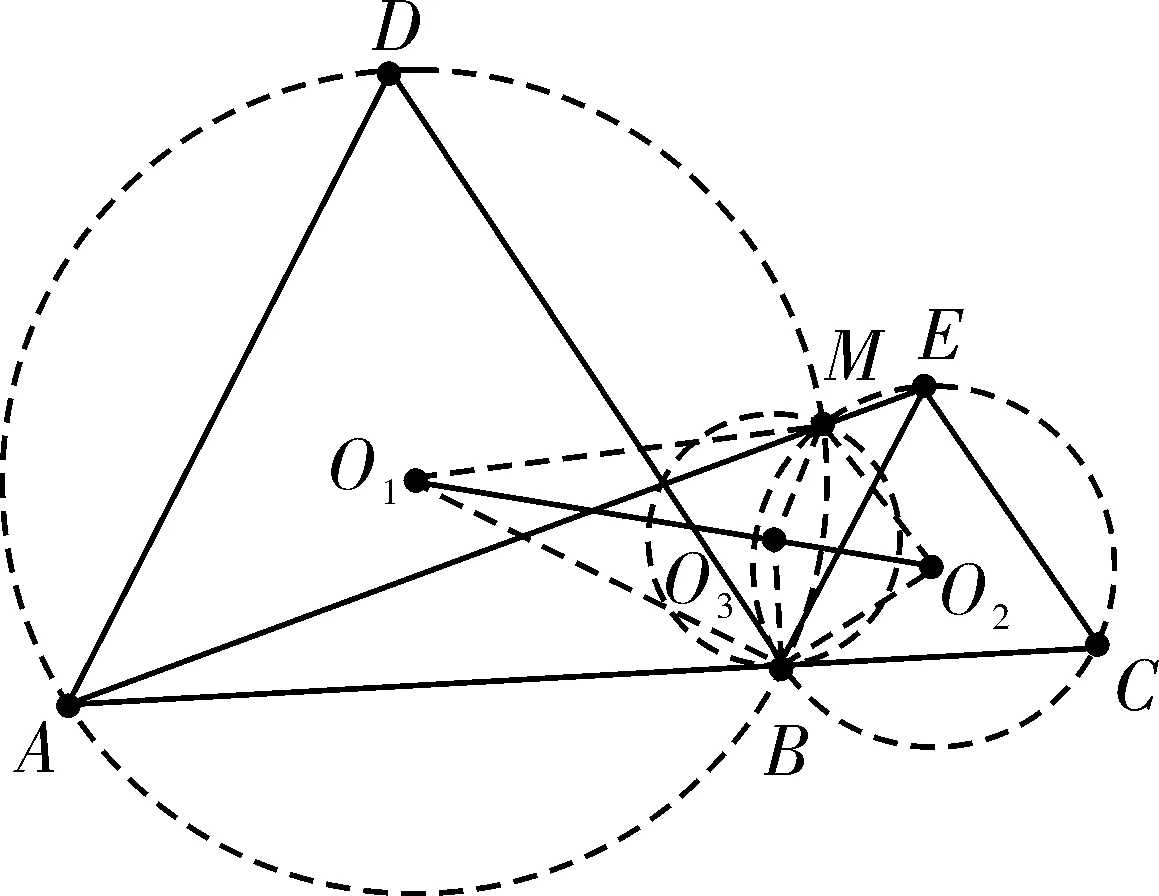
图5

由前面讨论可知，该题中的部分条件对于部分结论来说是多余的，因此，不断“去伪存真”，寻找出相应的结论是由哪些条件得出。

如图6，当A，B，C不在同一条直线上时，A，B，M，D和B，C，E，M分别四点共圆的条件并没有破坏，但是四边形PBQM对角互补的性质遭到了破坏，因此P，B，Q，M四点不共圆，同时对应的结论③不成立，其余结论依然成立。

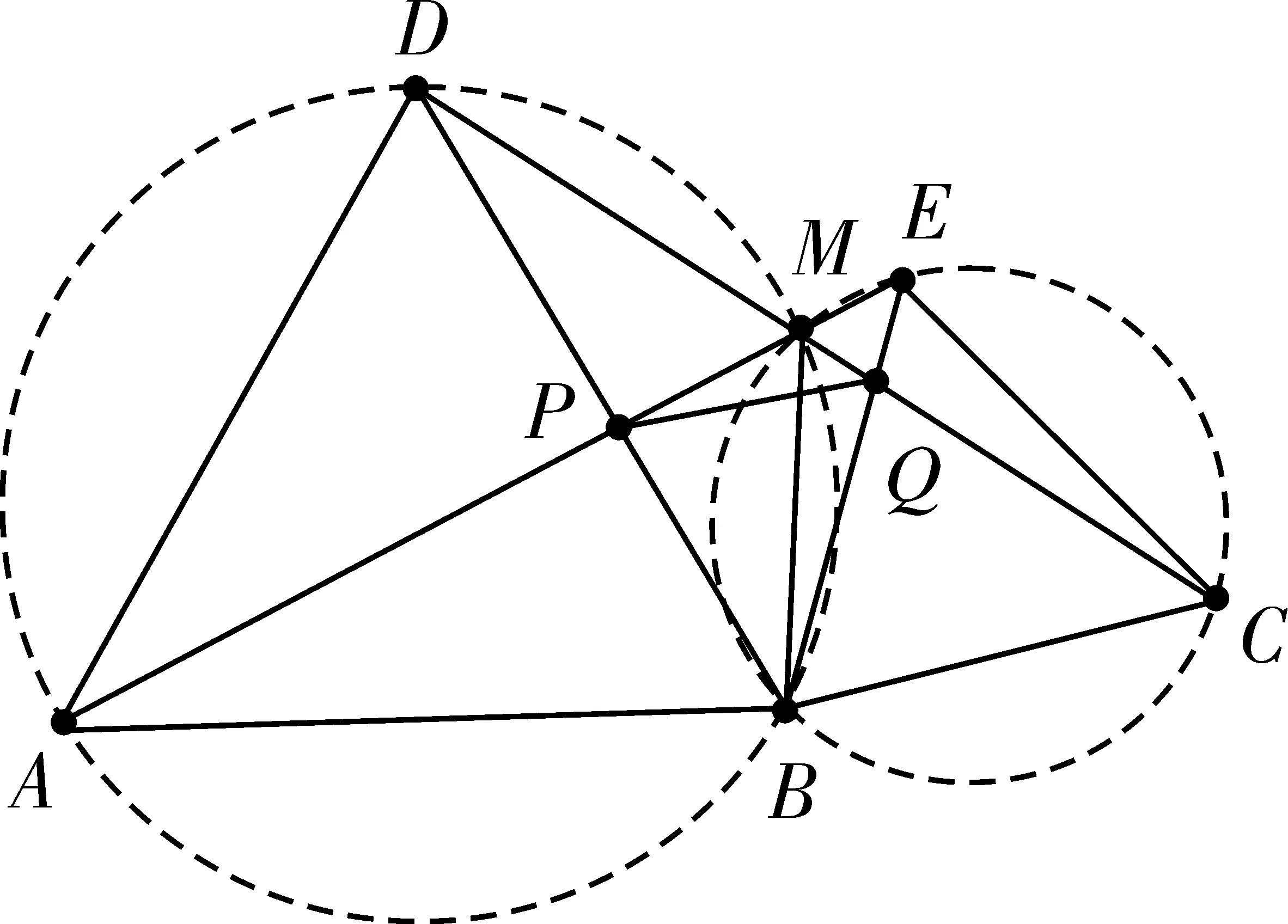
图6

四、图形变换

借助图形旋转的观点认识几何或几何问题能使得我们在动手操作的过程中获得对图形元素及位置关系与数量关系的深刻认识，变被动解题为主动尝试，既有解题经验的积累，又有客观规律的本质把握。除了对图形进行旋转变换外，还可对图形的条件进行强化或弱化处理，从而产生新的图形，对比“新旧”图形，既有共性也有特性，不论共性还是特性，都可以通过图形变换命制“新题”。

(一)原图的旋转变换

对图6中的△BCE不断地绕点B逆时针旋转，当旋转到一定程度时，就会出现不同的情况，如图7中①就是旋转到点E恰好落在BD上的情况，图7中②是旋转到点A，C，E恰好在同一条直线上的情况，图7中③是点E落在AB上的情况，这些情况都能保证AE=CD，其中图7中①和②都可通过证明△ABE≌△DBC来实现，但是对这些特殊情况，部分学生无法通过常规办法来解决。因此，学会在特殊图形中如何寻找一般图形所具有的结论，也会有利于学生思维的培养。图7中③无法通过△ABE≌△DBC来得出结论AE=CD，但AE=CD的结论是显而易见的。

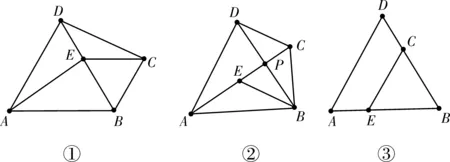
图7

(二)把等边三角形变成正方形后旋转变换

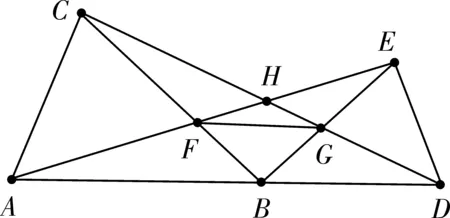
把原题的两个等边三角形变成两个正方形ABCD和CEFG，再把正方形CEFG绕点C逆时针旋转，就会出现如图8中①至⑤的情况。它们仍然满足BG=DE，且除图8中⑤外都可以通过证明△BCG≌△DCE来实现，同上述情况一样，虽然图8中⑤不存在△BCG和△DCE，但是BG=DE的结论也是显而易见的。

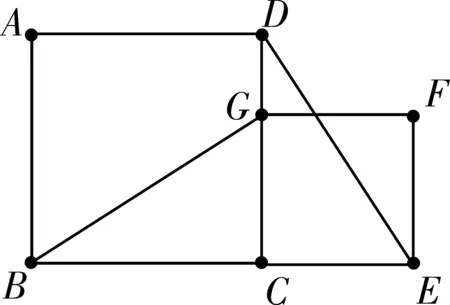
①

(三)把等边三角形变成等腰三角形后旋转变换

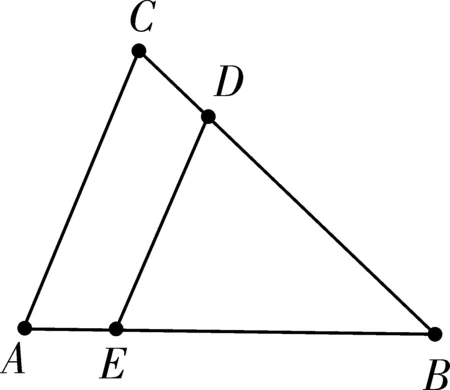
把原题的两个等边三角形变成顶角相等的两个等腰三角形ABC和BDE，再把等腰三角形BDE绕点B逆时针旋转，就有以下四种特殊情况，除图9中④外每一种情况都能通过证明△ABE≌△CBD来证明AE=CD，同样图9中④没有△ABE和△CDB，但是AE=CD显而易见。

①

限于篇幅，上面每种图形变换下的特性不再一一讨论，只是把图形列出来，让大家学会将每一种不同的图形改为一道习题的素材。习题源于教材，却广于教材，让学生做题时有据可考，有章可循，避免在“题海中挣扎”之困。

五、习题再编

①

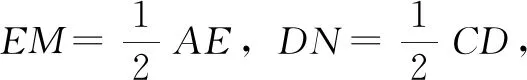
(1)在图10②中，AE与CD的数量关系是

(2)在图10③中，猜想BM和BN的数量关系、∠MBN与∠ABC的数量关系，并证明你的猜想。

此题是对图9④和图9②结合起来的一次改编，对问题(2)来说，也是通过证明△ABM≌△CBN来得出BM=BN，∠MBN=∠ABC的结论，如果没有问题(1)的证明就不可能有问题(2)的证明，如果没有掌握“母题”的证明，就不可能完成这道题目的证明。

六、教学建议

(一)寻根问祖，在教材中找出“母题”

数学家苏步青在中学时代曾做过上万道数学题，说明数学知识的获得和丰富离不开做题。但是有些同学做题无数，能力并未提高很多，说明无休止的、低效的“刷题”并不一定能真正提高能力。数学题目的层出不穷和千变万化，谁也不可能穷尽所有题目。如何有效、高效地做题，对习题的选择和“做法”就至关重要，实际上教材的习题一般都极具典型性和代表性。因此，做教材习题应是第一选择，只有反复研究教材习题，善于捕捉题目信息，找准习题中的隐含条件和干扰条件，拓展题目信息资源，从特殊到一般、从一般再到特殊，对每一道教材习题认真剖析、举一反三、融会贯通，才是获取数学知识、理解和掌握数学知识、提高数学能力的正确方法。

(二)善用教学软件，为数学思维插上翅膀

随着多媒体技术的飞速发展，各种教学辅助软件的问世为数学发展插上了腾飞的翅膀。例如，借助几何画板或GeoGebra等软件，可轻松获得结论，同时易于观察到哪些结论在图形变化的过程中保持不变，从一般和特殊的各种互换过程中，哪些结论会随之改变，这些软件往往能帮助我们突破瓶颈。当然，“对于教学软件的使用也应讲究‘法’，其使用应以激发学生思考、探索为目的”。“学会理解计算机给出的答案，知其所以然”。要在借助工具解决问题的基础上进一步思考工具背后的“数学本质”，还要把其中的“理”说清楚、想明白，而不是简单地停留于问题的机械解答。

(三)充分利用教材习题资源命制试题，避免“押题”“刷题”之困

一道高质量的数学题一定能在教材中找出“母题”，一定让学生在看到这个题目时感到似曾相识，但又从未见过。教师要在引导学生透彻研究这道题后会“通一片”，要让两个看似不同的题目形成知识之间的迁移和互通。教师要命制这样的试题，就要在教材中寻找题目源，深挖教材习题，反复研磨教材习题，不怕在教材习题上浪费时间，只有把教材习题研究透彻，才能避免“押题”“刷题”之困，所谓磨刀不误砍柴工。