深空探测采样返回起旋分离动力学仿真分析研究
2021-02-24朱佳林殷新喆韩润奇柳翠翠曾福明
朱佳林,殷新喆,朱 汪,吴 琼,韩润奇,柳翠翠,曾福明,刘 芃
(北京空间飞行器总体设计部,北京 100094)
0 引 言
深空探测采样任务完成后,返回器需以稳定的姿态再入返回(返回器重新进入地球大气层,并在地球着陆的过程称为再入返回),以确保安全、平稳落入地面指定区域[1]。某深空探测采样因其独特的空间构型布局和任务的复杂性,要求返回器(不具备姿态控制能力)以起旋(返回器与主探测器分离时,绕其分离轴线旋转)分离的方式实现再入姿态稳定。如美国[2-3]发射的“星尘号”、“起源号”和“OSIRIS-REx”,日本[4]发射的“隼鸟”和“隼鸟2号”,以及欧空局[5]未来发射的“MarcoPolo-R号”等深空探测采样返回任务,其返回器均采用起旋式分离,实现再入稳定。
航天器在轨起旋分离方法主要有两种:1)再入返回前,主探测器带动返回器同时旋转,转速达到预设时通过弹射机构将其弹推,如“星尘号”和“起源号”任务返回器;2)通过设置在主探测器和返回器之间的分离机构(如“隼鸟号”和“隼鸟2号”)或是助推小火箭点火,实现返回器在轨起旋分离要求,如“实践十号”[6]返回式卫星。前者对主探测器性能要求较高,且自旋速度较低,需要消耗能源来实现,不利于主探测器的后续拓展任务。而助推小火箭方法主要针对大型返回式卫星,可实时调节在轨姿态,但对返回器位置安装有严格要求。相比之下,针对深空探测再入返回任务,采用无源式起旋分离机构具有质量轻、深空环境适应性强、简单可靠、安装要求低等优点,因此具有更好的应用前景。
航天器在轨分离一般采用多刚体系统动力学分析方法研究其分离姿态及特性。文献[7]研究了分离机构不同设计方法和分离策略,确保微纳双星在轨分离性能的稳定性;文献[8]建立了星箭分离数学模型,分析了皮卫星质心偏离量、分离弹簧与舱门扭簧弹性系数对入轨初始姿态影响,且在轨飞行数据验证了仿真的正确性;文献[9]针对月球取样返回器伞舱盖弹射分离过程的安全性进行了仿真研究,研究结果表明伞舱盖弹射分离速度合理,分离安全可靠。综上所述,参考文献中所研究的航天器均为线性分离,即采用弹簧分离推杆机构,实现两器在轨直线式分离,无起旋要求。目前,国内嫦娥五号[10]深空探测采用跳跃式成功实现了再入返回,且返回舱设有主动调姿功能,而起旋式再入返回因其独特的任务要求和技术难度,还未曾有过验证。
本文针对某深空探测采样返回器,起旋式分离实现再入姿态稳定的任务,在完成起旋分离机构参数设计与优化后,针对影响返回器分离姿态相关参数进行了分析。通过建立返回器起旋分离动力学仿真分析模型,并基于综合敏度的分析方法,进而识别系统参数对返回器初始分离姿态及其性能的影响。最后,通过开展最为敏感设计参数偏差耦合分析以及多参数偏差覆盖性仿真分析,验证了系统参数选择的合理性。
1 起旋分离过程简述
深空探测采样返回任务设立起旋分离机构2位于主探测器1和返回器3之间,且中间穿插有连接主探测器和返回器的电缆连接器24,如图1所示。起旋分离机构主要由手指组件21、压紧组件22、滚轮组件23、起旋组件25和起旋弹簧26组成。
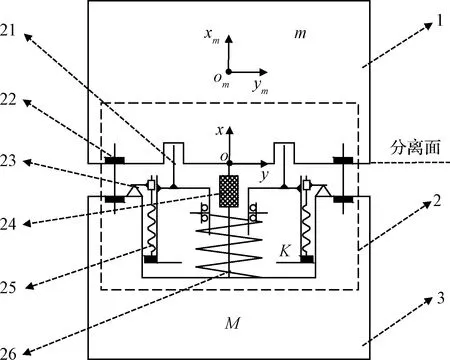
图1 起旋分离机构工作原理Fig.1 Working principle of the spin mechanism
起旋分离机构通过刚性连接与主探测器下沉凹孔相连,返回器则通过压紧组件连接在主探测器支撑结构上,以承受发射段振动载荷。主探测器支撑结构内部设有起旋组件与手指组件刚性连接,且手指组件与返回器底端沟槽为接触安装。
再入返回时,首先电缆连接器断电解锁。其次火工解除压紧组件约束,位于底部的起旋弹簧(初始受压)施加起旋组件沿x轴方向推力,此时起旋组件(外侧周围120°均布三个由直线段→圆角段→螺旋段依次过渡的滑槽,其中滑槽形状如图2右侧)外侧滑槽在滚轮组件(滑槽与滚轮组件的位置关系如图2左侧)的约束下,实现直线运动过渡到螺旋运动。其中,直线段运动是为确保能够完全脱开电缆连接器,以免对返回器分离姿态造成影响;圆角段运动是为了使起旋组件能够平滑过渡到螺旋段,以免滚轮组件发生强碰撞接触而卡滞;螺旋段运动是为实现起旋组件通过手指组件拨动返回器绕x轴方向旋转,进而达到起旋目的。当起旋弹簧到达最大工作行程时,起旋组件机械限位停止运动,而返回器将在惯性的引导下继续螺旋运动,此时手指组件将从返回器低端的沟槽中退出,进而实现返回器起旋后与主探测器分离。
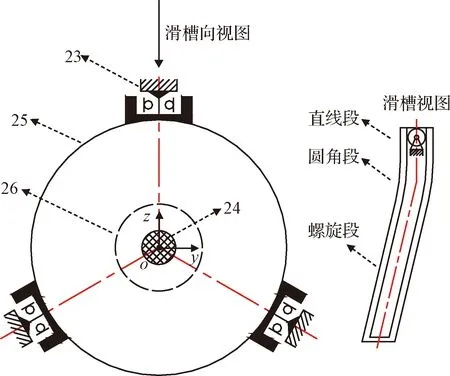
图2 滑槽与滚轮组件位置及滑槽形状示意Fig.2 Location relation of roller assembly and chute assembly
返回器采用弹道直接再入返回,与主探测器分离后,就无法再进行任何姿态及轨道调整[11]。因此,为精确预报落点,返回器与主探测器在实现安全可靠分离的前提下,对其初始分离姿态及性能提出了相关要求,见表1。

表1 返回器起旋分离技术指标Table 1 Technical indicators of the spin separation
2 动力学建模与分析
2.1 动力学建模
起旋分离机构螺旋传动几何参数对分离角速度具有直接影响,而起旋弹簧力学参数作为唯一动力源将直接影响起旋后的分离速度。根据图1所示的机构原理对上述参数进行初步设计。
在主探测器上,以返回器和主探测器的分离面中心构建参考坐标系O-xyz;坐标原点O为分离面中心,垂直于分离面从主探测器指向返回器方向为x轴正向;y,z方向平行于分离面且遵循右手定则。返回器质心坐标系为Om-xmymzm,坐标原点Om为返回器质心位置,三轴与参考坐标系同向。
当返回器沿x轴方向分离时,在不考虑起旋弹簧阻尼、结构为刚体无变形且接触绝对光滑条件下,根据动量守恒、动能定理和角动量守恒,在参考坐标系下有:
(1)
式中:M和m分别为主探测器与返回器的质量;v1x和v2x分别为主探测器与返回器沿x方向速度分量;v1x0和v2x0分别为主探测器与返回器在参考坐标系下的初始速度分量,其中两器相对于参考坐标系初始速度分量为0,即v1x0=v2x0=0;K为起旋弹簧弹性系数;x1和x2分别为起旋弹簧工作始末对应的压缩量;JMx和Jmx分别为主探测器与返回器x方向的转动惯量;ωMx和ωmx分别为主探测器与返回器沿x方向的角速度分量,ωMx0和ωmx0分别为主探测器与返回器在参考坐标系下的初始角速度分量,其中两器相对于参考坐标系初始角速度分量为0,即ωMx0=ωmx0=0。
根据式(1)可知,两器在x方向分离过程中的相对速度Vx为:
Vx=v2x-v1x
(2)
将螺旋滑槽展开并根据螺旋传动定理可知:
(3)
式中:λ为螺旋滑槽的螺旋升角;θmx为返回器沿x轴的起旋角度;H为螺旋高度;dp为螺旋中径。
对式(3)进行时间t求导如下:
(4)
将系统简化为单自由度简谐振荡模型,则起旋分离时间t为:
(5)
根据上式即可确定起旋分离机构螺旋传动几何参数、起旋弹簧参数和两器分离时间。
返回器质心位置的不对中会存在惯性张量,进而存在各向分离姿态的变化。为进一步分析起旋分离各向姿态角及角速度,根据刚体动力学动量定理和角动量定理有[8]:
(6)
式中:v=[vxvyvz]T为返回器分离速度;ω=[ωxωyωz]T为返回器角速度,ω×为对应的叉乘矩阵;L=[LxLyLz]T为角动量;Fext=[FxFyFz]T为返回器外力;Mext=[MxMyMz]T为返回器外力矩。角动量由下式可得:
(7)
式中:Ixx,Iyy,Izz分别为绕返回器质心各坐标轴的转动惯量;Ixy,Iyz,Ixz,Iyx,Izy,Izx分别为惯性积,其中Ixy=Iyx,Iyz=Izy,Ixz=Izx。
根据式(6)和式(7)可得:
(8)
假设弹簧对中安装,则有:
(9)
式中:Cmy为返回器y向质心位置;Cmz为返回器z向质心位置;Δx为起旋弹簧分离过程中的变形量。
假设电缆连接器插拔过程中所需x方向外力Fe为:
(10)
式中:Fp为电连接器分离力;FV为电连接器插针/孔分离力;sx为返回器沿x轴方向的分离位移。
从动力学方程可以看出,只要知道返回器质量、质心位置和主惯性矩及惯性积,通过多次迭代即可求得在理想状态下(不考虑接触摩擦、碰撞及轨道形状等)返回器的初始分离姿态。
2.2 动力学分析
起旋分离机构中存在许多接触和约束,且螺旋滑槽的形状由直线段依次过渡到圆角段和螺旋段。因此,基于刚体动力学动量定理和角动量定理的理论解析计算,将无法充分反映实际运动情况。基于上述动力学理论模型,在ADAMS软件中完成起旋分离机构三维实体建模,其中模型的属性及参数定义见表2,并构建各组件之间的摩擦接触和约束,见表3。
表2中动力回转轴为起旋弹簧中心线相对返回器绕x轴回转轴线的安装位置,标称设计值为0 mm,即为弹簧中心线与返回器绕x轴回转轴线重合。返回器与手指组件的接触、滚轮组件与起旋组件的接触均赋予摩擦属性,其中静摩擦系数设置为0.3,动摩擦系数设置为0.1。

表3 动力学仿真分析边界设置Table 3 Boundary condition setting of simulation analysis
表3中主探测器设为零重力环境下的自由边界,能够真实模拟返回器与主探测器在轨分离状态。
电缆连接器在断电解锁后,需起旋分离机构在初始直线段5 mm运动时,提供45 N力将其拔开。为确保电缆连接器完全脱开,另设插针在插孔内5 mm距离,脱开需额外力5 N。针对标称设计工况(参数见表2)进行分析,仿真时间设为0.3 s,仿真步数设为1000。各项指标分析结果见表4。

表4 标称工况下在两器分离时刻的仿真分析结果Table 4 Simulation analysis results of nominal conditions
如图3所示,从分离开始,返回器相对主探测器速度Vx逐渐增加,到0.0975 s直线段行程结束。在0.0975~0.104 s期间,起旋组件进入圆角过渡段,速度Vx逐渐降低,而角速度ωx逐渐增加至稳定值90.04(°)/s。进入螺旋段时线速度Vx又开始逐渐增加至882.68 mm/s分离结束。分离时间t为0.177 s,线速度Vx和角速度ωx分别为0.883 m/s和90.04(°)/s,在标称工况下均满足指标要求。
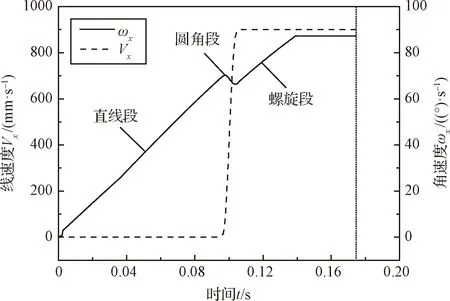
图3 返回器线速度Vx和角速度ωx时域关系Fig.3 The relation of Vxand ωxof the returner
如图4所示,起旋组件在直线段和螺旋段时,返回器姿态角速度ωy和ωz较为平稳。而在圆角处时由于滑槽与滚轮组件存在间隙,使得起旋组件与滚轮组件发生接触碰撞,导致返回器姿态角速度瞬间上升,接触稳定后瞬间下降至平稳。分离时刻,返回器姿态角速度ωy和ωz分别为-0.2871(°)/s和0.1258(°)/s,合成姿态角速度ωyz为0.3134(°)/s<1(°)/s,满足指标要求。
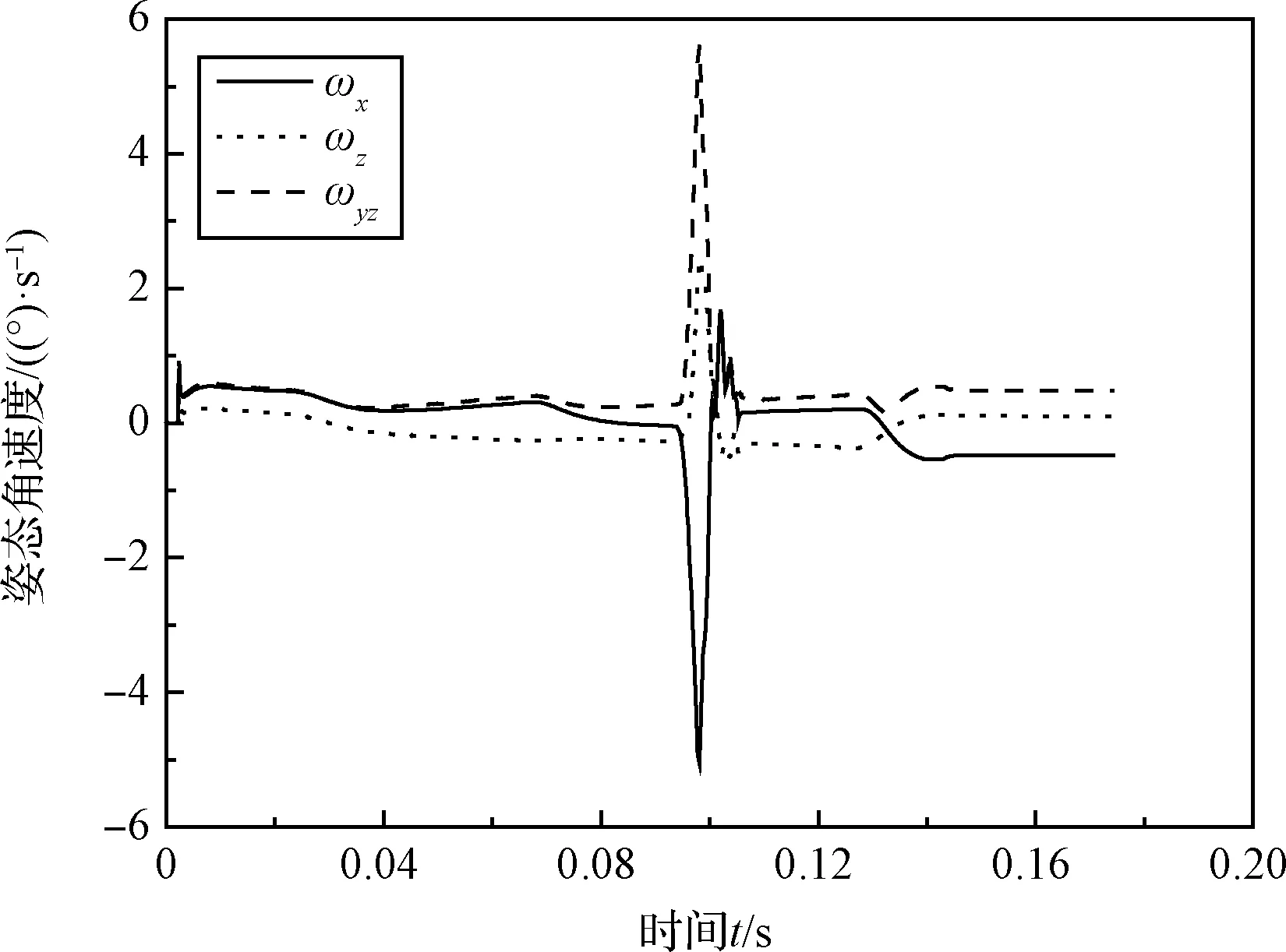
图4 返回器姿态角速度时域关系Fig.4 The relation of the attitude angular rates of the returner
如图5所示,采用滚轮组件在起旋组件外周围均布的三个螺旋滑槽里进行接触,并约束起旋组件的运动轨迹。当位于起旋组件下方的起旋弹簧采用理想对中安装方式时,会使得返回器从初始到分离时刻,姿态角Ay,Az的变化幅值较小。其中,返回器姿态角Ay和Az在分离时刻为-0.0026°和-0.0101°,均小于0.1°,满足指标要求。
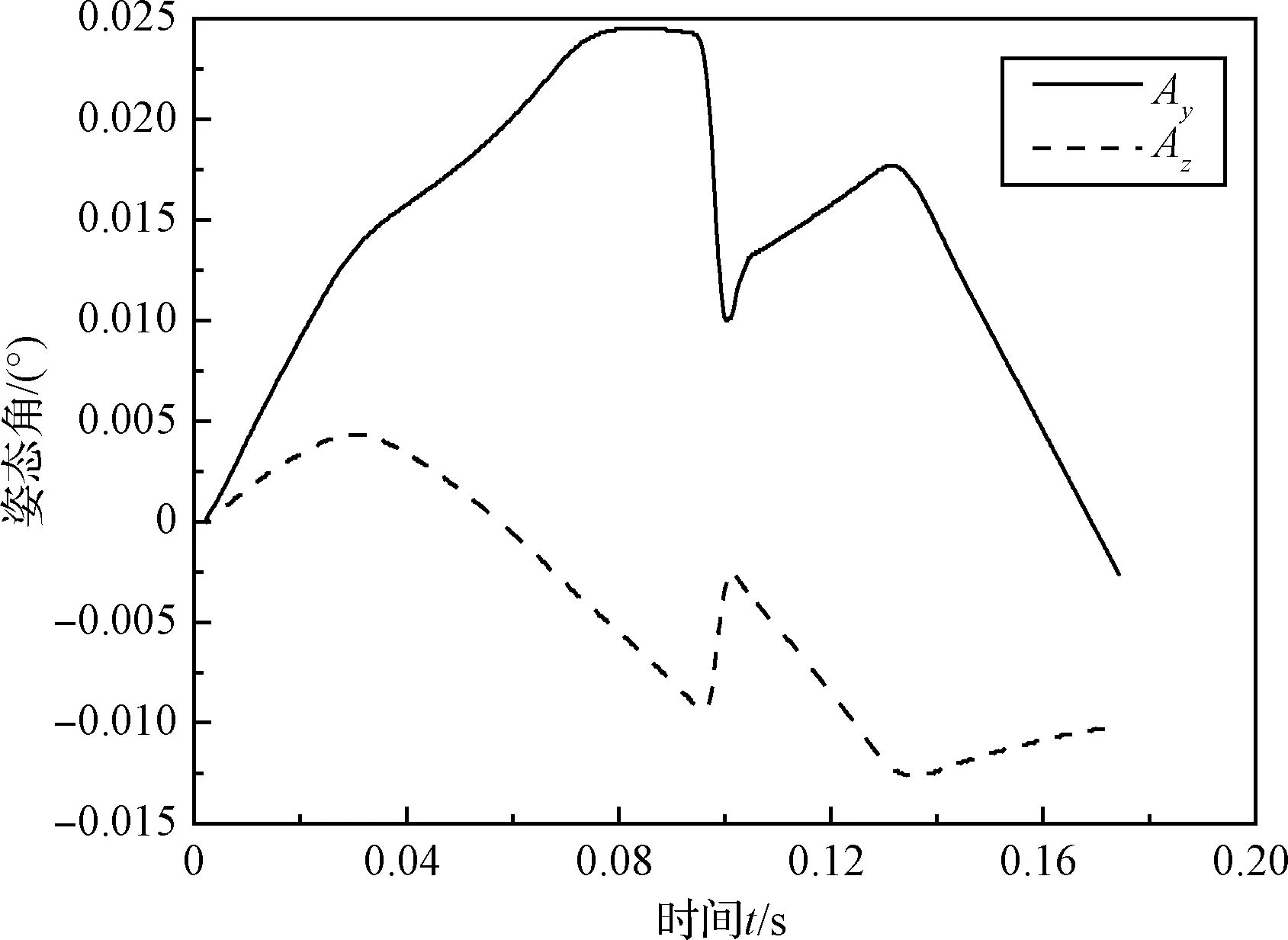
图5 返回器姿态角Ay和Az时域关系Fig.5 The relation of the Ay and Az of the returner
3 综合敏度分析
3.1 综合敏度分析理论
为合理设计起旋分离机构工程样机,在后续装配和试验过程中提供技术指导,本文针对表2中的影响参数进行综合敏度分析。基于上述动力学仿真模型,建立起旋分离机构参数化分析模型。影响参数的取值区间选取为标称值(表2各参数的初始设计值)的±40% 进行敏度分析。设响应函数为fik(ai1,…,aij,…,ain),则每个影响参数ai相对fik的敏度Sik如下:
(11)
其中,fik为响应矩阵(k=1,2,3,4,5分别为线速度Vx、角速度ωx、姿态角Ay、姿态角Az以及合成姿态角速度ωyz的响应矩阵);k为响应矩阵编号;m为影响参数的个数,本文共分析18个影响参数,即m=18;i为影响参数的编号;n为每个影响参数在标称值±40%区间内的取值个数,本文采取标称值的5%为设计增量进行依次取值,每个影响参数均在区间内取值为17个,即n=17;j为影响参数取值个数的编号;Δaij为影响参数ai在取值区间的增量。
为分析影响参数ai(i=1,2,…,m)在响应函数fik(k=1,2,…,5)的比重,对上述敏度分析结果进行归一化处理,得到综合灵敏度Uik(即敏度占比,为无量纲百分比常数)如下:
(12)
综合敏度分析结果中,正值代表设计响应矩阵与影响参数为正相关,负值即为负相关。
3.2 线速度Vx敏度分析
线速度综合敏度Ui1(i=1,2,…,m;m=18)分析结果如图6所示。起旋弹簧初始载荷对线速度影响最大,占所有设计参数比重的43%。返回器质量、转动惯量Ixx和弹簧弹性系数分别占比-28%、-12%和-9%,且呈负相关,其他变量影响相对较小。起旋组件在进入螺旋段时,返回器产生与线速度成定比关系的旋转运动,这使得转动惯量Ixx对返回器线速度具有显著的敏度效应。
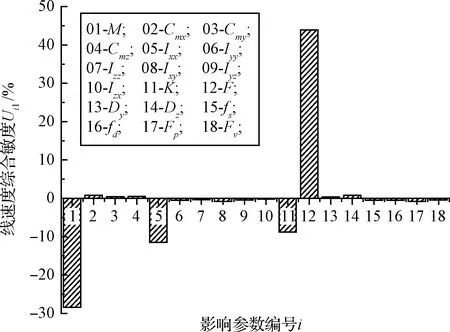
图6 返回器线速度Vx综合敏度柱状图Fig.6 The histogram of the comprehensive sensitivity of the returner linear velocity Vx
3.3 角速度ωx敏度分析
角速度综合敏度Ui2(i=1,2,…,m;m=18)分析结果如图7所示。起旋弹簧初始载荷对角速度的影响最大,占所有设计参数比重的32%。返回器质量、返回器y向质心、弹簧弹性系数和转动惯量Ixx分别占比23%、5%、5%和4.8%,其他变量影响相对较小。
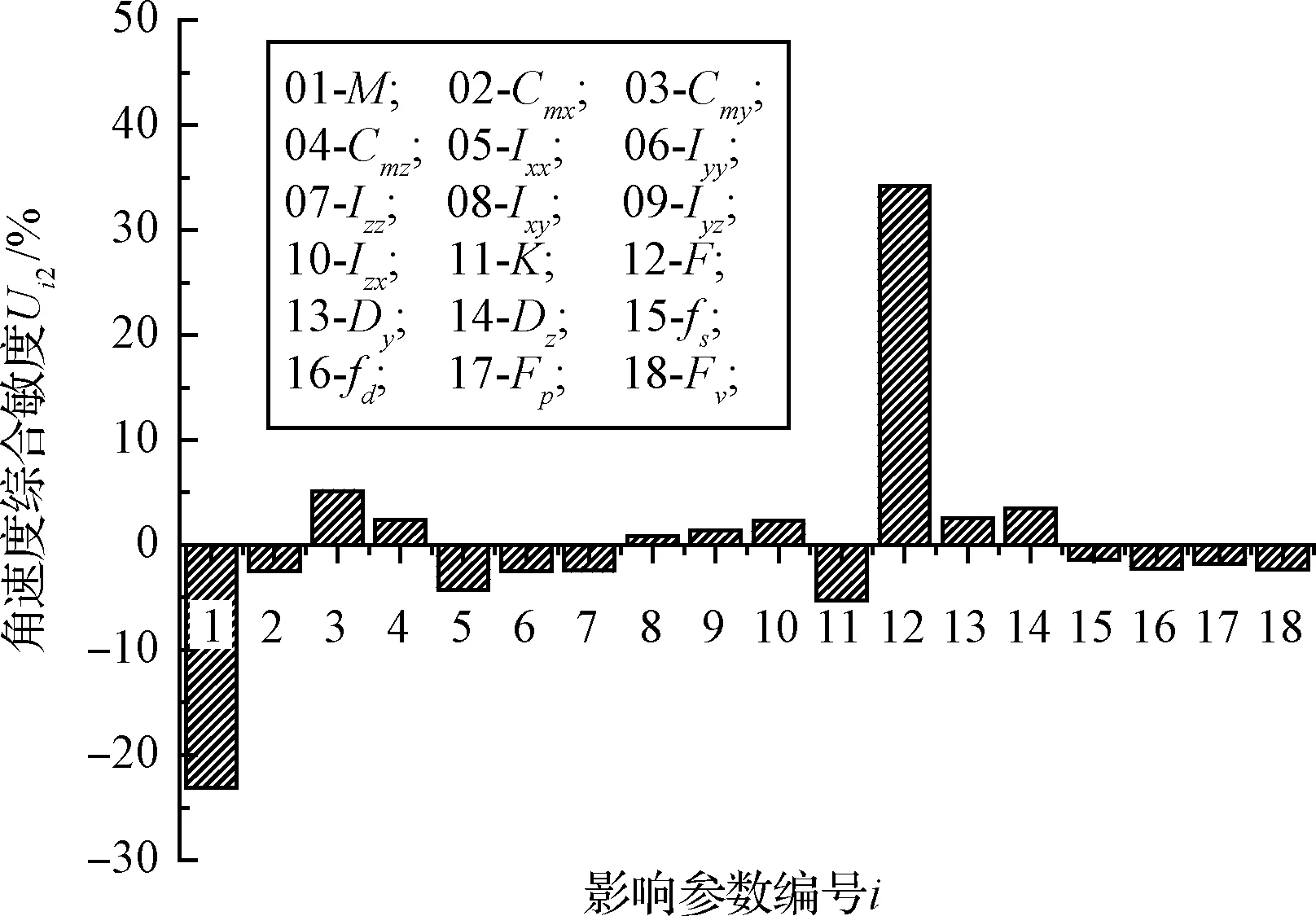
图7 返回器角速度ωx综合敏度柱状图Fig.7 The histogram of the comprehensive sensitivity of the angular velocity ωx of the returner
3.4 姿态角Ay敏度分析
姿态角Ay综合敏度Ui3(i=1,2,…,m;m=18)分析结果如图8所示。返回器z向质心和惯性积Ixy对姿态角Ay的影响最大,占所有设计参数比重的60%,其他参数所占的比重相对较小。起旋组件在进入螺旋段时,返回器的反向质心和惯性积对其自身分离的姿态角具有显著的敏度效应。

图8 返回器姿态角Ay综合敏度柱状图Fig.8 The histogram of the comprehensive sensitivity of the attitude angle Ay of the returner
3.5 姿态角Az敏度分析
姿态角Az综合敏度Ui4(i=1,2,…,m;m=18)分析结果如图9所示。返回器y向质心和惯性积Izx对姿态角Az的影响最大,占所有设计参数比重的61%,其他参数所占的比重相对较小。起旋组件在进入螺旋段时,返回器的反向质心和惯性积对其自身分离的姿态角具有显著的敏度效应,这与姿态角Ay综合敏度分析结果相对应。
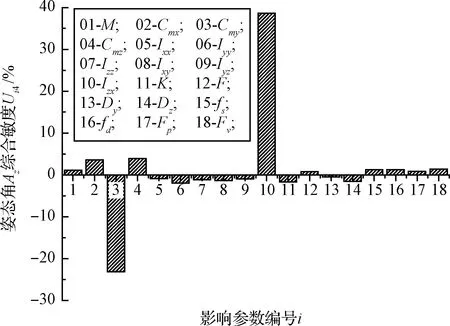
图9 返回器姿态角Az综合敏度柱状图Fig.9 The histogram of the comprehensive sensitivity of the attitude angle Az of the returner
3.6 合成姿态角速度ωyz敏度分析
合成姿态角速度敏度Ui5(i=1,2,…,m;m=18)分析结果如图10所示。z向动力回转轴偏差对合成姿态角速度的影响最大,占所有设计参数比重的17%。y向动力回转轴偏差、返回器z向质心、惯性积Ixy占比在5%~12%之间。其他设计参数占比相对较小,平均为1%~5%之间。
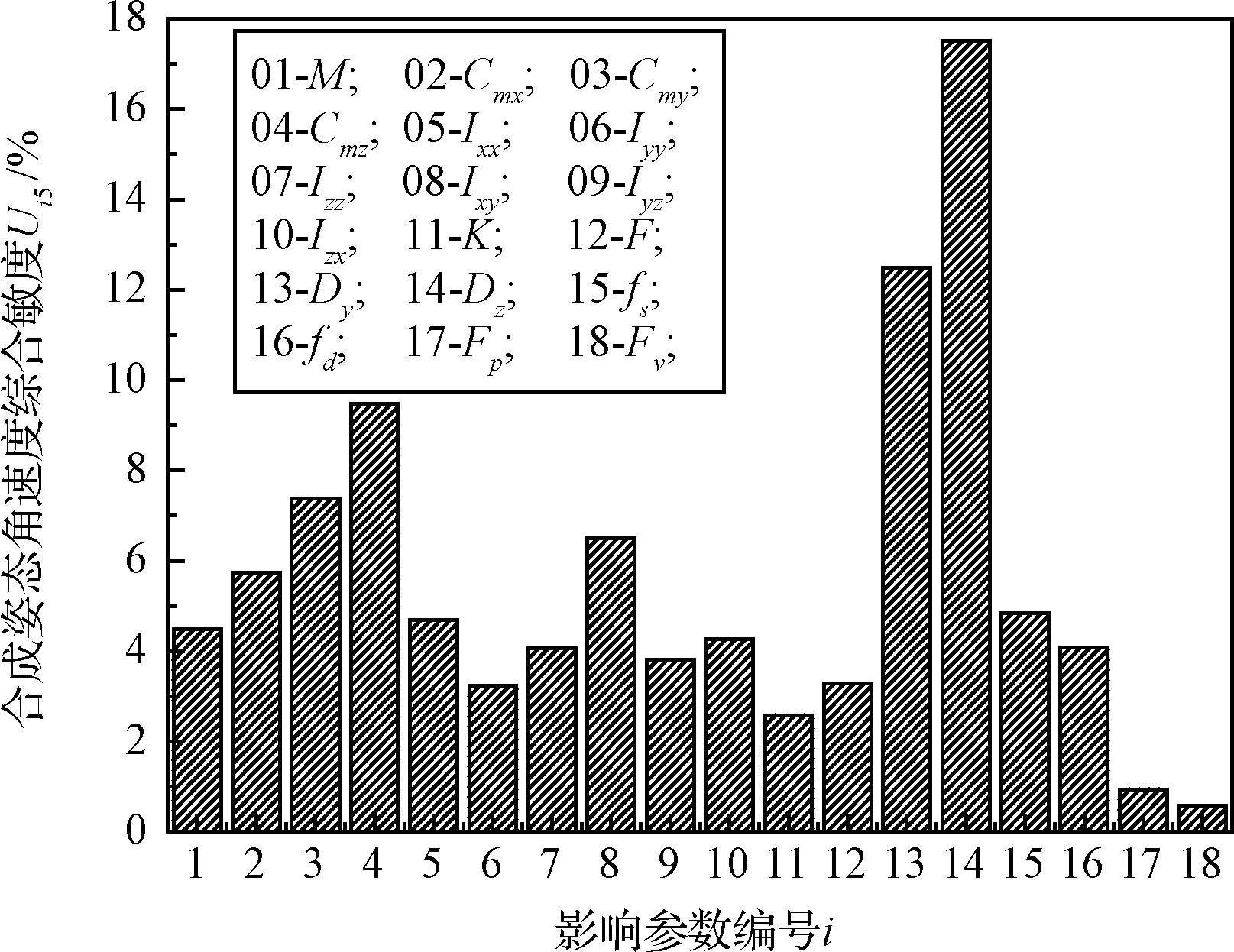
图10 合成姿态角速度ωyz综合敏度柱状图Fig.10 The histogram of synthetic attitude angular velocity ωyz comprehensive sensitivity
根据敏度分析结果显示,返回器合成姿态角速度受多参数综合影响。从敏度占比成分来看,针对起旋分离机构单机产品,控制其动力回转轴偏差对降低合成姿态角速度具有更好的效果,而控制机构接触摩擦系数,追求更高的润滑表面对有效降低合成姿态角速度贡献相对较小。针对供配电分系统,电缆连接器插拔力对返回器姿态影响甚小。针对返回器分系统,有效控制返回器y,z方向质心偏差和惯性积Ixy可以有效降低合成姿态角速度。为进一步指导工程设计,本文将针对最为敏感的参数,即动力回转轴偏差和返回器质心偏差进行耦合分析。
4 敏感偏差耦合分析
根据综合敏度分析结果,为进一步分析起旋分离机构动力回转轴y,z向偏差,返回器y,z向质心偏差分别对合成姿态角速度ωyz的综合影响,需要对其进行耦合分析。
4.1 动力回转轴各向偏差耦合分析
动力回转轴偏差和返回器质心位置偏差调节量均设为±0.5 mm,如图11所示。在设计偏差0±0.5 mm区间内,y向动力回转轴向负向偏移,z向动力回转轴分别向正向偏移时,有效降低合成姿态角速度的75.3%。向相反方向偏移时,对合成姿态角速度影响较大,甚至可能会超过技术指标要求。因此,起旋分离机构在工程设计与装配中,有意偏移动力回转轴位置,使其落在第二象限较为适中。但仅限于区间0±0.5 mm之间,本文经过分析得到,如扩大偏差范围会使得姿态角速度急剧上升。

图11 动力回转轴各向偏差对角速度ωyz耦合影响Fig.11 The influence of the dynamic rotation axis deviation on the coupling of angular velocity ωyz
4.2 返回器横向质心偏差耦合分析
如图12所示。返回器y,z向质心同时向负向偏移时,有效降低合成姿态角速度的84.6%。向相反方向偏移时,对合成姿态角速度影响较大,甚至可能会超过技术指标要求。因此,返回器分系统在配质心时可有意使其落在第四象限。但仅限于区间0±0.5 mm之间,本文经过分析得到,如扩大偏差范围会使得姿态角速度急剧上升。
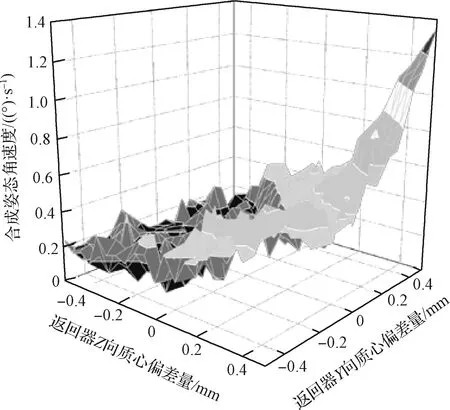
图12 返回器横向质心偏差对角速度ωyz耦合影响Fig.12 The influence of the deviation of the transverse centroid of the returner on the coupling of angular velocity ωyz
5 多参数覆盖性分析
标称值仿真只能预测各设计参数在理想状态下的起旋分离机构动力学特性。在工程装配和实施过程中,各参数会在一定偏差范围内波动。为更真实模拟在轨环境以及对产品性能的预测,确保在各项偏差条件下满足技术指标要求,仅进行标称仿真还无法满足评估条件。本文基于上述仿真进一步采用蒙特卡洛方法,验证起旋分离机构在多参数偏差影响下的分离特性。各参数偏差范围设置见表5,其中所有参数均按照服从正态分布设置。

表5 蒙特卡洛仿真各设计参数偏差取值范围Table 5 Monte Carlo simulation parameter deviation range
蒙特卡洛仿真时,在偏差区间范围内随机抽取样本5000次。根据标称工况分析的起旋分离时间,设置仿真时间为0.3 s,对分析结果进行统计,得到各响应结果如表6、图13-17所示。其中,返回器起旋分离时间t≤0.2 s,远小于指标要求,限于篇幅,本文不再对分离时间进行统计。
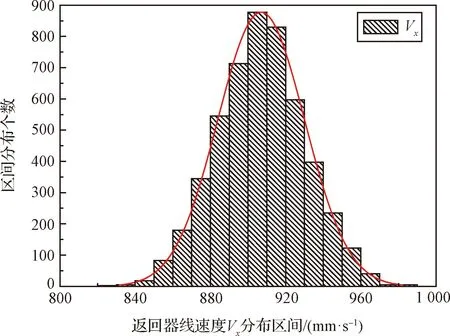
图13 返回器线速度Vx统计分布Fig.13 Statistical distribution of the velocity Vx
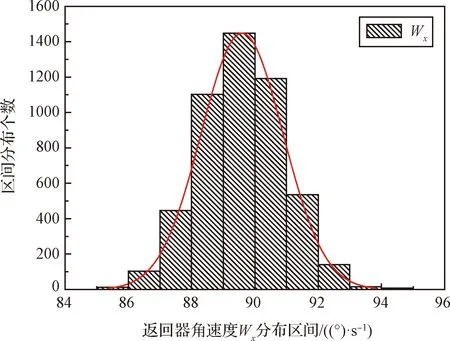
图14 返回器角速度ωx统计分布Fig.14 Statistical distribution of the angular velocity ωx
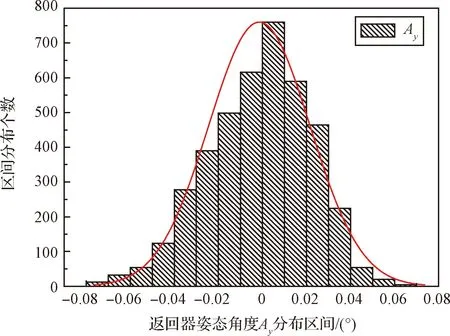
图15 返回器姿态角度Ay统计分布Fig.15 The statistical distribution of the attitude angle Ay
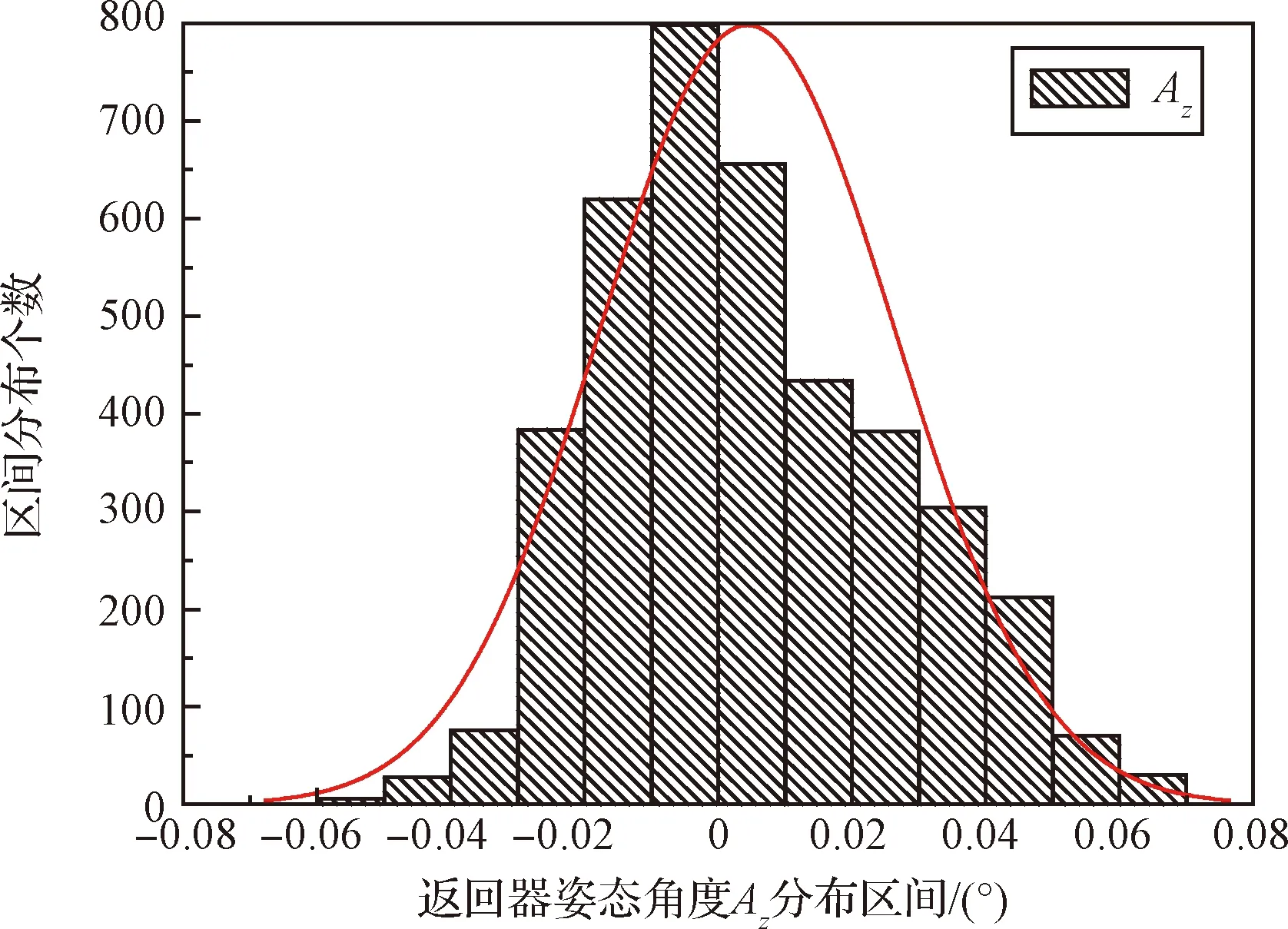
图16 返回器姿态角度Az统计分布Fig.16 The statistical distribution of the attitude angle Az
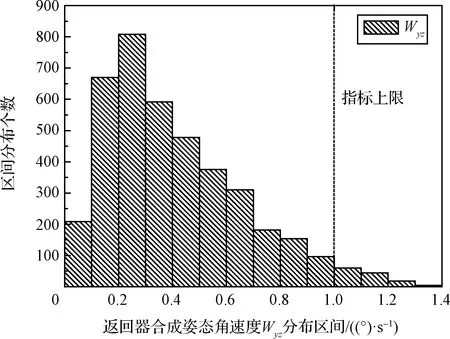
图17 返回器合成姿态角速度ωyz统计分布Fig.17 The statistical distribution of the synthetic attitude angular velocity ωyz
根据表6数据统计结果可知:
1)线速度Vx和角速度ωx均服从正态分布。考虑±3σ区间内分别为878.80~948.18 mm/s和85.677~93.513(°)/s。由此可知,在多参数偏差影响下线速度和角速度均能满足设计指标。
2)返回器姿态角Ay和Az均服从正态分布。考虑±3σ区间内分别为-0.071~0.067°和-0.067~0.077°。由此可知,在多参数偏差影响下各向姿态角均能满足设计指标。
3)合成姿态角速度ωyz在±3σ区间内为-0.235~1.073(°)/s,略超过技术指标上限1(°)/s。根据图17所示,合成姿态角速度ωyz并不服从正态分布。可按百分位数法统计,在5000次样本点中,有98个样本点超出1(°)/s,由此可知返回器合成姿态角速度ωyz有98.04%概率落在1(°)/s指标范围内。
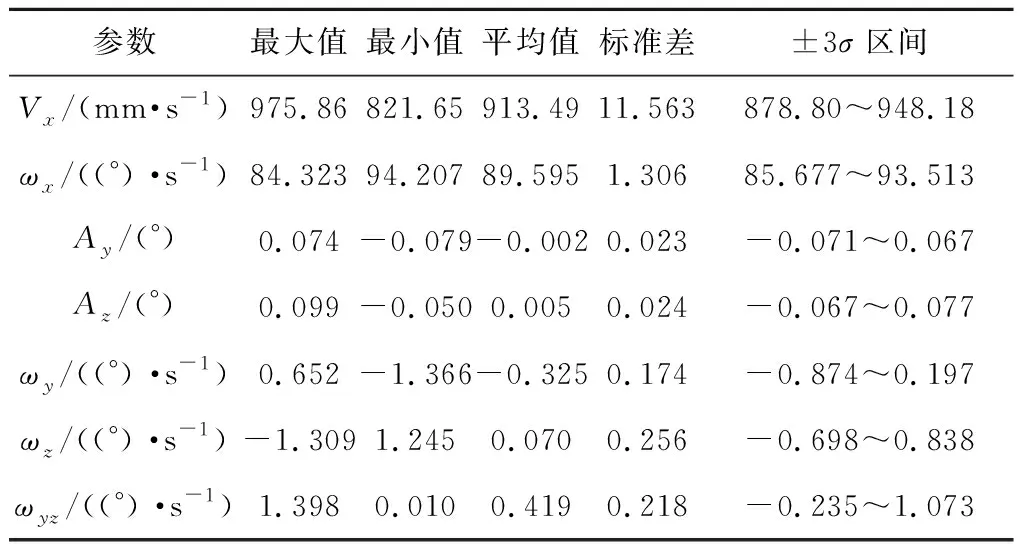
表6 蒙特卡洛仿真分析结果统计Table 6 Monte Carlo simulation analysis results statistics
6 结 论
返回器再入返回初始姿态对深空探测采样返回任务具有重要影响。本文在起旋分离动力学理论研究基础上,通过建立返回器起旋分离ADAMS仿真分析模型,以评估多参数偏差对返回器初始分离姿态及性能的影响。
1)经多参数综合敏度分析,结果显示,起旋分离机构动力回转轴位置及返回器横向质心偏差,是影响返回器分离姿态的关键因素。因此,起旋分离机构需严格控制动力回转轴线偏差,返回分系统需严格进行质心配平设计。
2)经最为敏感参数偏差耦合分析,结果显示,在有效偏差范围内,动力回转轴位置落在第二象限内,可降低合成姿态角速度的75.3%;返回器质心位置落在第四象限内,可有效降低合成姿态角速度的84.6%。
3)经多参数覆盖性分析,结果显示,除返回器合成姿态角速度98.04%的概率会落在1(°)/s指标范围内,其他技术指标均满足要求,能够实现返回器再入返回初始姿态的稳定性要求。
