建筑材料对室内空气质量影响的数学模型研究
2021-02-24孙涵
孙 涵
(黑龙江省佳木斯大学,黑龙江 佳木斯 154002)
屋内空气质量,即在标准情况下干燥空气的纯净度。左右屋内空气质量的元素通常是甲醛、VOC对身体有害的事物或颗粒。数学建模是检验这部分物质并完成考评的有效工具。相异的室内环境必须启用相异的考评模型来处置,所以,界定模型的使用环境、建模流程与运用成效有着极大的价值。笔者依照时间次序与相异的用途,简介了六大较为经典的考评模型。笔者将建筑原料当成屋内空气污染源,并权衡到屋内外通风进气的情况,构建建筑原料对屋内空气质量影响的数学模型,并完成污染物浓度的预估与运算。
1 经典模型论述
1.1 适当环境
潘宝骏在2000年抽检了福州五个歌舞厅,搜集1989-1998年66个检测点四大参数,以SPSS10.0.5实施统筹解析。
1.2 建模流程
明确四大空气质量数据的类别编码,并由此构建4D列联表:
a:气温(TEM)。TEM <22℃为LT,≥22℃为HT;b.负离子浓度(NI)。NI<7为LI,≥7为HI;c.二氧化碳(CO2)。CO2 <0.07为LC,≥0.07为HC;d.细菌总数(BAC)。BAC <19为LB,≥19为HB。
4D列联表内,与每格观测频次(uijkl)相呼应的每格期望数据是m(ijkl),数学模型是:
lnm(ijkl) =u+u1(i)+u2(j) +u3(k)+u4(l)+
u12(ij) +u13(ik)+u14(il)+u23(jk)+u24(jl)+u34(kl)+
u123(ijk)+u124(ijl) +u134(ikl)+u234(jkl)+
u1234(ijkl)式中:U:期望频次自然数据的均数;
u1(i)~u4(l):主效应,即各数据对应的效应;
u12(ij)~u24(jl):1阶交互效应;
u123(ijk)~u234(jkl):2阶交互效应;
u1234(ijkl):3阶交互效应。
这类独立数据数目与总格子数的模型中被叫做饱和模型。
2 数学模型构建
2.1 基础方程
住房是各类建筑原料堆砌的屋内小环境,屋内空气环境质量被多类元素与相互间所影响,包含建筑创设、装修作业、物主活动、屋外空气质量等。屋内空气质量数据通常是由屋内空气构成,屋内空气中的污染物质形成于屋内与屋外的污染源,而且与屋内通风换气率、污染物降解洁净度相关。依照物质守恒规律,屋内空气污染物数目的均衡方程能够被表述成:屋内空气污染物数量=屋外流入的污染物量+屋内形成的污染物量-屋内排泄的污染物量。
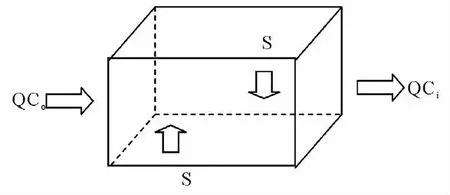
图1 屋内污染物扩散模型
2.2 数学建模
建筑原料根据其特性与用途能够分成基础建筑原料与装修用料,两者很难严格区分。例如水泥混凝土、自然石料、人造板料、涂料、漆料等。虽然建筑原料的品种不一,然而其污染物的散发原理是相同的。微分方程(一)两边除以V,能够得到:
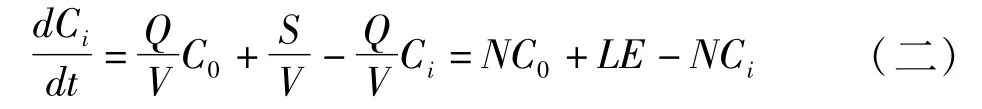
算式内,L-屋内建筑原料填充率,平方米/立方米;E——建筑原料中污染物散发速度数据,mg/m2·h1;N为屋内外空气互换率(次数/小时);建筑原料内气体污染物的散发速度是动态的,通常情况下,污染物散发速度伴随用时而下降,那么:

算式内,E0——建筑原料中污染物原始散发速度,mg/m2·h;k——建筑原料内污染物散发速度的衰减数据,h-1。
将算式(三)代入微分方程式(二),那么:
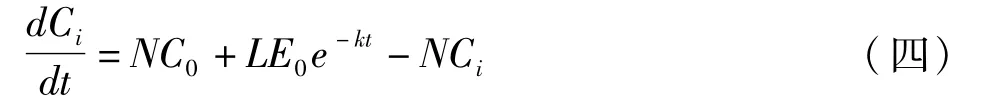
解以上微分方程阶段,权衡到边限条件中的原始时间t=t0=0,屋内污染物的原始浓度与屋外污染物的浓度是相同的,那么Ci=Cj0=C0。运算算式(四)获得时间t,屋内空气中某类污染物的浓度是:
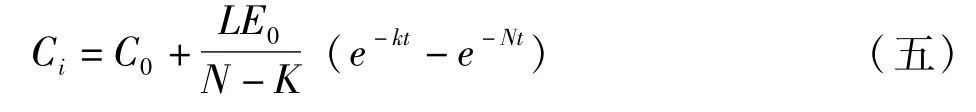
方程(五)被叫做建筑原料对屋内空气质量影响的数学模型,映射出屋内建筑原料填充率、屋内外空气互换率、屋外空气污染物浓度对屋内空气品质的影响程度,此数学模型被用在屋内空气质量的考评与预估中。
3 数学模型的具体运用
数学模型(五)适于预估通风环境中屋内空气污染物的浓度,例如某住房内装修创设中加权浓度的预估测算。房屋大小是5m×4m ×3m,房屋占地V=60立方米。使用天然通风模式,屋内气温是(23±2)摄氏度,相对湿度是(45±5)%。挑选建筑市场上某种细木板料实施装饰,挥发出有机物甲醛。根据下列两类状况、三大方法创设,预估与运算屋内加权浓度在半年内的改变情况。

表1 材料使用情况表
1)首类状况:屋内空气互换率N=1.0h-1,细木工材料填充率依次使用L1、L2、L3三类创设预案,算式A=L×V运算出材料运用量,见表1。
2)第二类状况:屋内细木工材料填充率L=1.0m2/m3,空气互换率依次使用N1、N2、N3三类通风预案,算式Q=N×V运算出通风进气量。
3)明确模型数据
使用小规模环境实验舱均衡浓度模式,明确数学模型(五)内的E0与k两大数据。细木工材料加权的原始发散速度E0=3.57mg/m2·h-1,甲醛发散速度衰减数据k=0.0078h-1.把E0与k代入数学模型(五)可以获得:
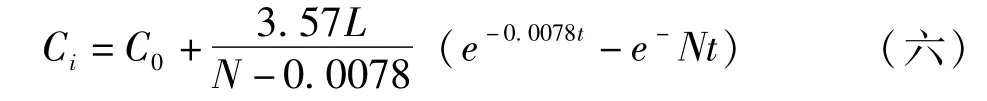
4)居民住宿区甲醛浓度预估模型
①适用环境
王琨等从2003年1-12月对哈尔滨市七大区域内新装修大概1年的住宿区完成了屋内甲醛测定,得到246分样品。成果说明:检测率是100%,浓度范畴是 0.017 - 1.302mg/m3, 年 度 平 均 数 据 是0.219mg/m3。
②建模描述
任意抽查55个住宿区房屋,权衡到影响甲醛浓度的六大元素,也就是屋内气温、屋内空气含湿量、屋内换气情况、房屋材料占地、材料质量级别(依照情况分成1-5级)与房屋体积。
依照这部分元素与实际测量的浓度间的关联,构建屋内空气内甲醛浓度预估模型:
C=fQ(rT+a)(bD+e)/(i+jN/G)
③使用成效
使用统筹软件SPSS12.0融合具体参数对算式实施非线性运算,获得待定数据。所以获得下列经验算式:
C=0.582Q(0.108T-0.907)
(0.001D+0.193)/(1.401+1.093N/G)
拟合数据R2=0.7728。为检测模型的可行度,将没有参与建模的36组参数代入运算出预估数据;对比实际值与预估值,回归统筹得出有关数据R2=0.8670,标准偏差是0.053mg/m3。实际测得的甲醛浓度 范 畴 是0.036-0.610mg/m3,平 均 数 据 是0.210mg/m3,标准偏差是0.024mg/m3。
成果显示,预估模型可以有效地估测屋内空气中的甲醛浓度。
4 结语
综上所述,本文构建的建筑原料对空气质量影响的数学模型,是基于污染物的质量平衡理论与动态挥发速度而获得的,有着运算算式简易、物理意义清楚的特征。此模型适合屋内通风的环境,建筑原料挥发气体污染物的浓度预估中,能够为建筑与装修工程对屋内空气质量的影响考评提供数据支撑。在屋内装饰装修与通风空调的创设阶段,也能够为建筑品种的挑选、建筑原料运用量与屋内外通风量的明确提供参考依据。在屋内温湿度既定的状况下,数学模型内的原始挥发速率E0与衰减数据k与建筑原料的种类、特性相关。
