基于LANL卫星的等离子体层顶位置模型改进
2021-02-23彭辉王志强
彭辉, 王志强
1 南京航空航天大学航天学院, 南京 210016 2 中国科学院空间天气学国家重点实验室, 北京 100190
0 引言
地球等离子体层位于内磁层,是其重要组成部分,这里的等离子体密度大(n>108m-3)而温度约为3000~5000 K(Horwitz et al., 1986),它是电离层到外磁层的过渡区.等离子体层底(即电离层顶)是氧离子为主到氢离子为主的过渡带,由于成分主要为H+,比重约占85%,所以等离子体层也叫质子层,在等离子体层中粒子含量较高的还有He+和O+(Horwitz et al., 1986).等离子体层顶的密度梯度很大,位置随磁层活动而变,一般在3RE~6RE(RE表示地球半径,1RE=6372 km)范围内(Laakso and Jarva, 2001).等离子体层顶是等离子体层的外边界,对于内磁层的研究具有重要意义.
对等离子体层顶的研究从20世纪60年代至今已经历经数十年,虽然其形成机制极为复杂,但在理论和实际观测方面都取得了许多进展,目前主要有电场平衡(Nishida and Atsuhiro, 1966)和交换不稳定(Lemaire, 2001)两种形成机制,其中电场平衡形成机制提出早,比较经典,应用最为广泛.IMAGE卫星(Burch,2000)上搭载有一台EUV探测器(Sandel et al., 2000),能够对等离子体层中He+的30.4 nm极紫外辐射进行观测成像,来研究等离子体层的分布特征.通过观察EUV拍摄的图像,发现了等离子体层顶的许多特殊结构,包括羽状区、等离子体层肩、槽状结构等(Burch et al., 2001; Darrouzet et al., 2009; Buzulukova et al., 2008),其中羽状区的特征最为显著,对于等离子体层顶位置的研究至关重要.
为了更好的研究等离子体层顶,考虑到形成机制的复杂性,科学家们构造了许多经验或半经验的模型(Carpenter and Anderson, 1992; Gallagher et al., 2000; Sheeley et al., 2001; Moldwin et al., 2002; Cho et al. , 2015; Liu et al., 2015). Goldstein等(2014a,b,2017)也曾构造一个简单的以Volland-Stern(VS)电场(Volland, 1973; Stern, 1975)作为基础函数,太阳风电场Esw和地磁活动Kp指数驱动的PTP(plasmapause test particle)仿真模拟磁暴时期等离子体层顶,得到了比较好的拟合效果.之后,Goldstein等(2019)根据PTP模拟的数据和VS电场,构建了一个新的基于磁暴历元时间的等离子体层顶解析模型.
这个新模型虽然相较之前的模型第一次明确包含了羽状区,但总体上简单的将羽状区的形态演化过程分为两个时间段,缺乏磁暴情况下应有的动态变化.本文利用RBSP-A卫星输出数据对该模型进行了误差检验,并以LANL卫星测得的中等磁暴时期羽状区等离子体层顶位置数据为基础进行了模型的优化改进工作,体现出羽状区在磁暴峰值前后发生的漂移、延伸以及收缩过程,得到的结果与卫星观测数据更为符合.
1 等离子体层顶位置模型及误差检验
1.1 等离子体层顶位置模型
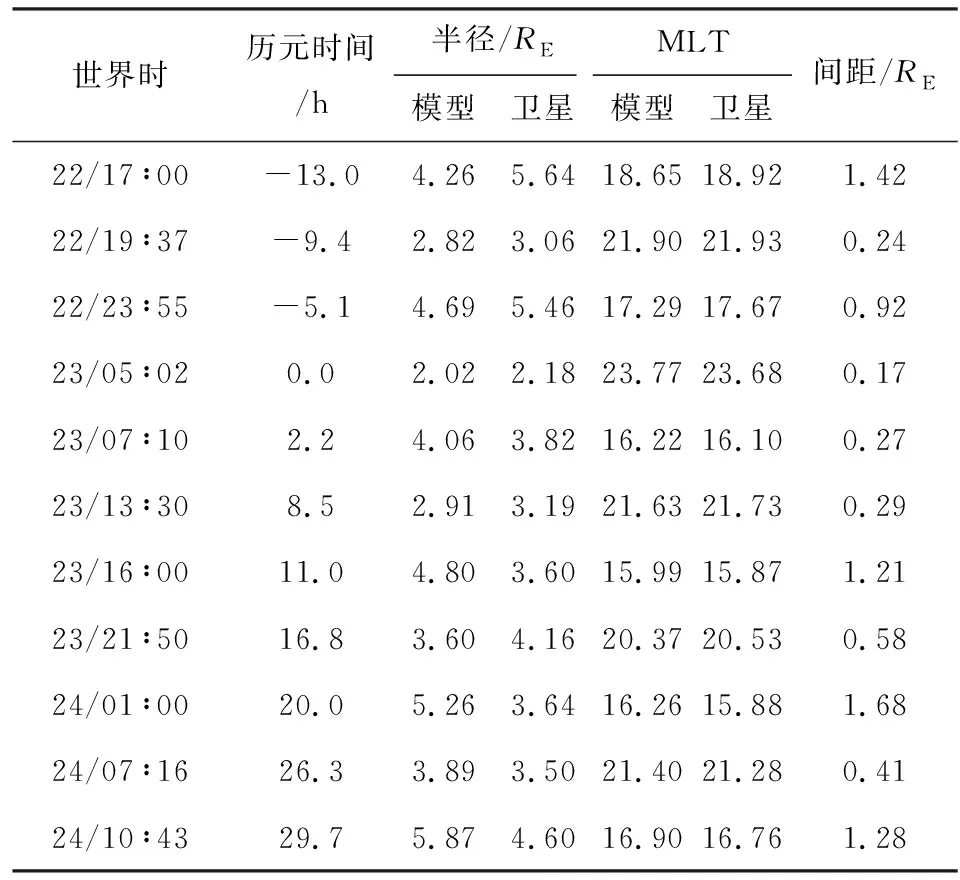
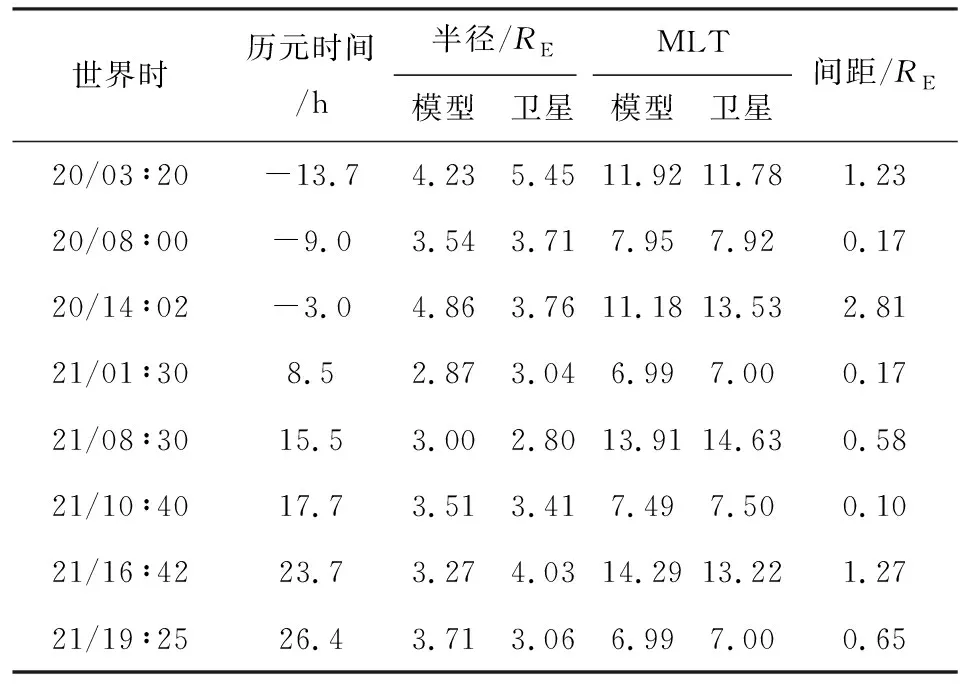
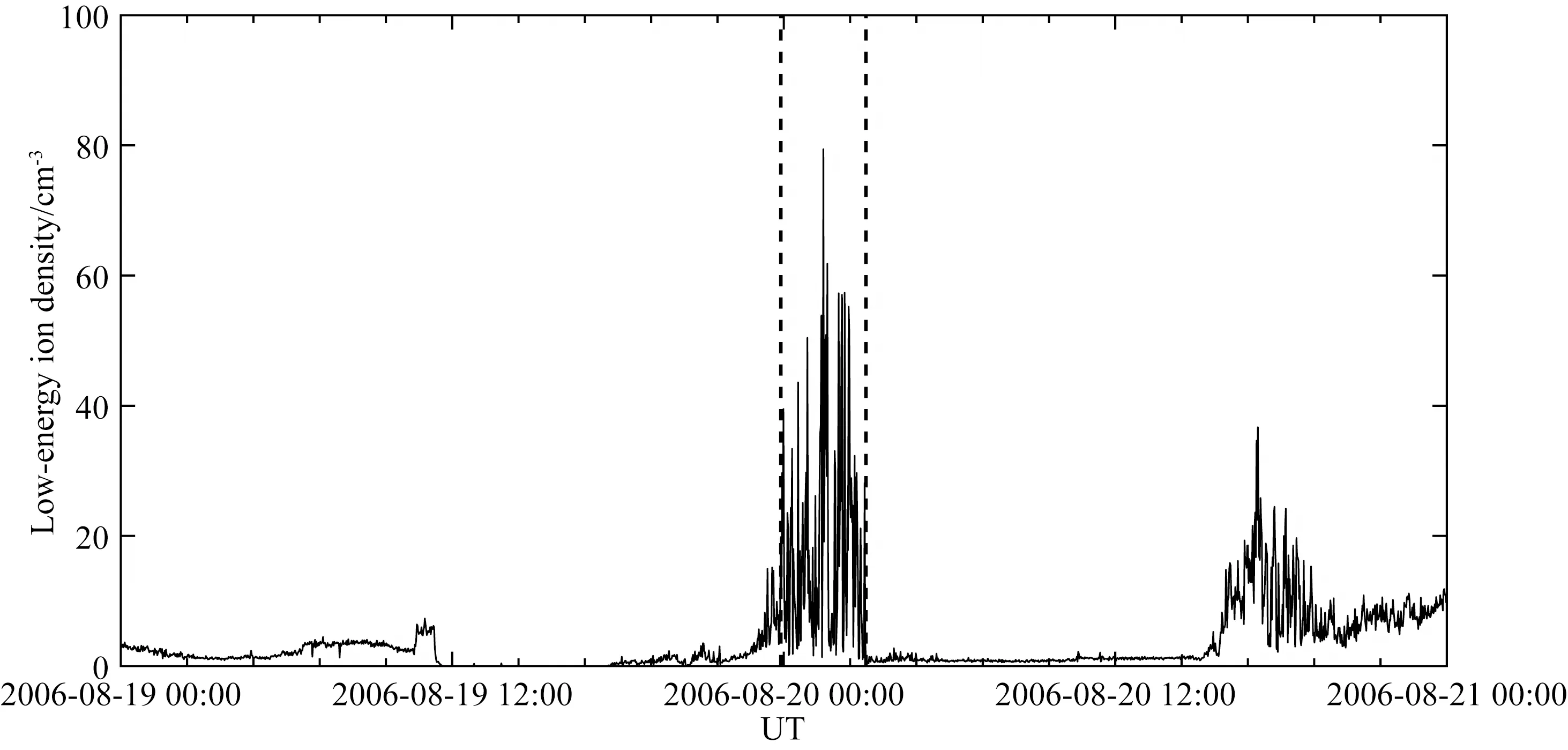
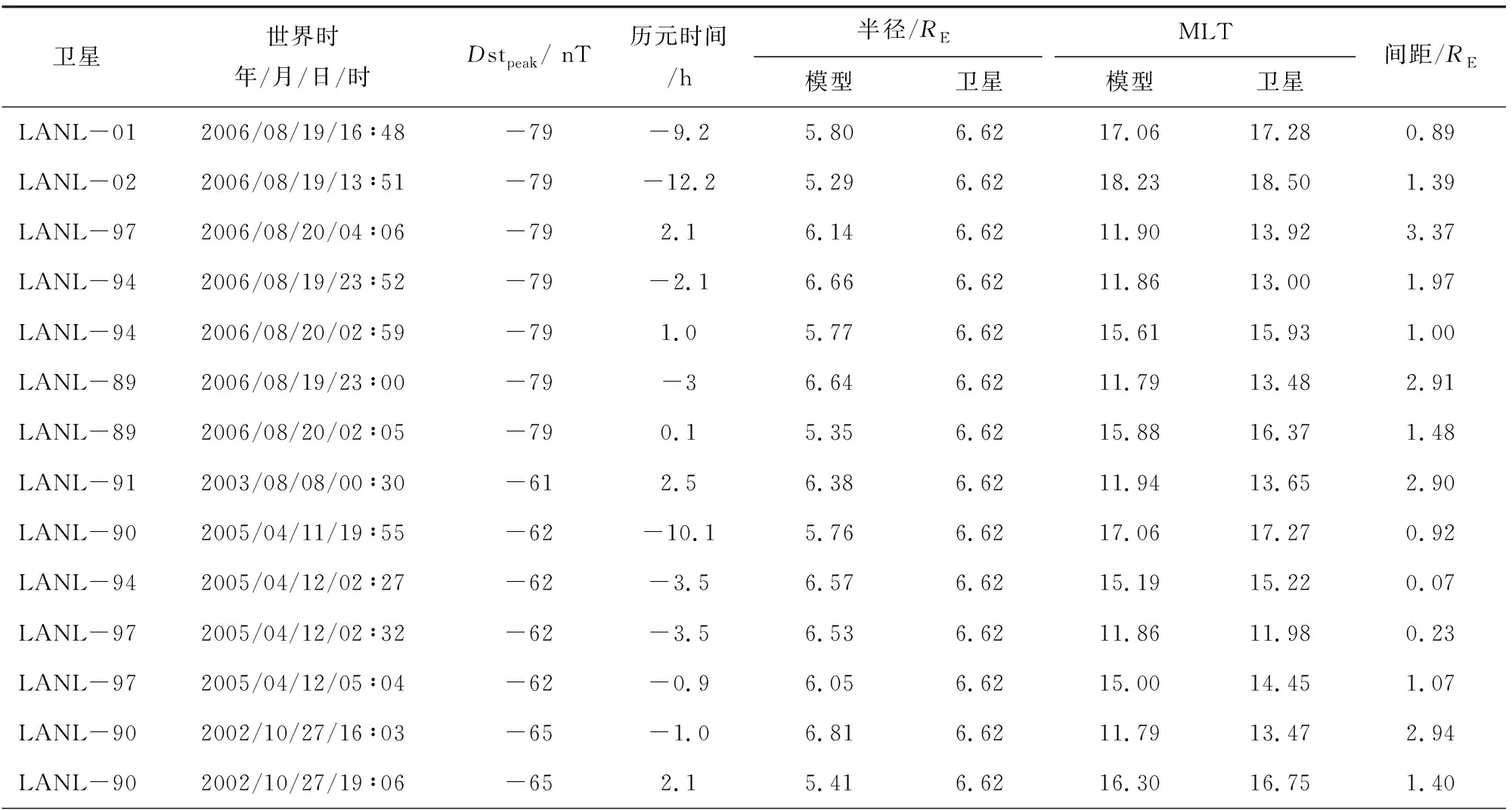
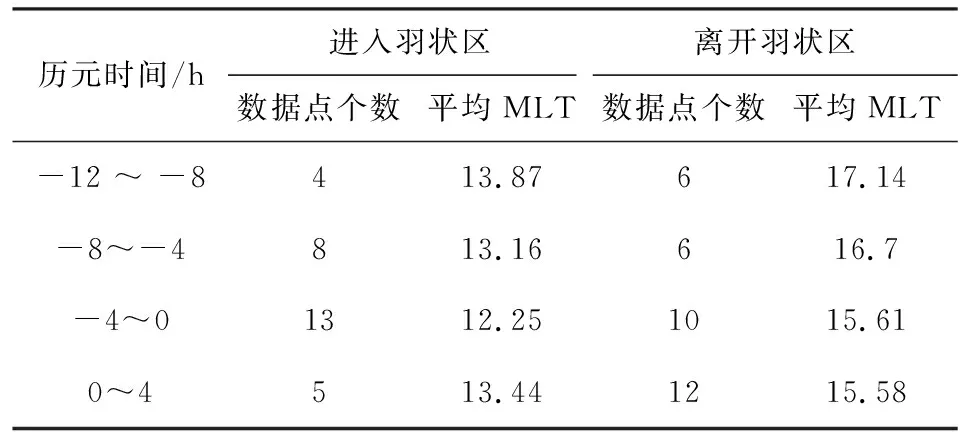
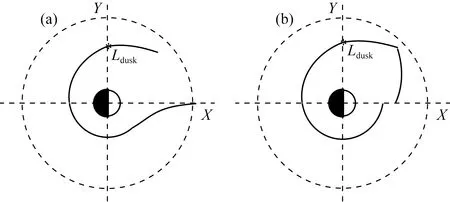
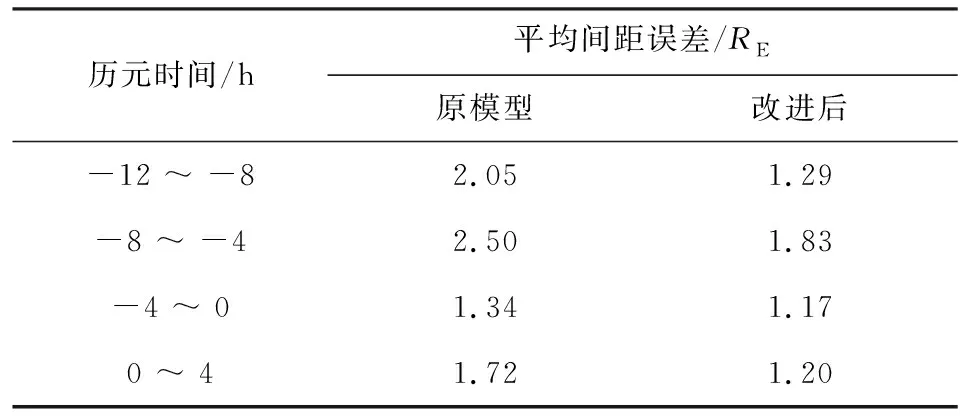
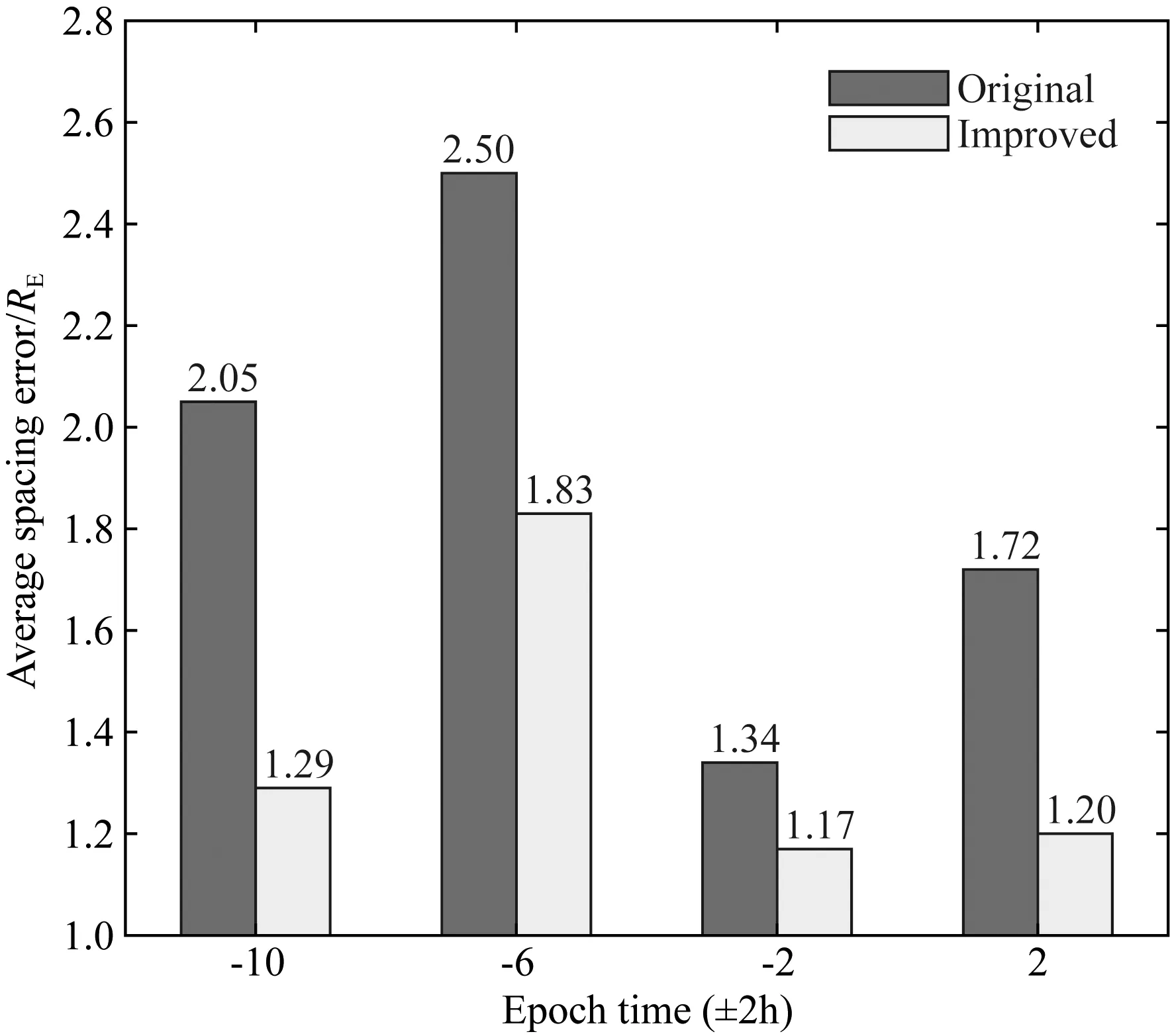
Goldstein等(2019)构建的这个等离子体层顶解析模型取决于历元时间(Tepoch),将磁暴事件中Dst指数出现峰值即Dstpeak时定为0时刻(Tepoch=0).对于中等磁暴(-120 nT 模型基于VS屏蔽电场,该电场在GSE坐标系下的等电势图如图1所示,图中X轴对应MLT=12,Y轴对应MLT=18.图中LCE(last closed equipotential)代表粒子闭合与开放漂移路径的分界线,蓝色、黄色、绿色和下方白色区域分别代表R2、R3、R1和R0的有效区域,它们的表达式如公式(1)中所示. D=csc3λ(sinλ-f3), (1) 图1 VS屏蔽电场等电势图Fig.1 Equipotential diagram of VS shielded electric field 式中λ是周向角,向着太阳的方向λ=0,向着黄昏方向λ=π/2.f=Φvs/Φs,Φvs为电场任意点电势,Φs表示在黄昏侧(MLT=18)电场为零时,即Ldusk处的电势. 该模型将磁暴演化过程分为两个不同的活跃时期,一部分是磁暴剧烈时期(-12 h≤Tepoch≤4 h),该时期的模型公式为: 18≤MLT<24:Lp=Ldusk·R3·g,f=1 00 09 15≤MLT≤18:Lp=Ldusk·R2·h,f=1 MLT=24或MLT=12:Lp=Ldusk·R0·g,f=1 (2) 式中S09=0.5033.另一部分是磁暴平缓时期(Tepoch<-12 h或Tepoch>4 h),模型公式如下: 18≤MLT<24:Lp=Ldusk·R3·g,f=1 00 12≤MLT≤15:Lp=Ldusk·R3·h·S15,f=1 15≤MLT≤18:Lp=Ldusk·R2·h,f=1 MLT=24或MLT=12:Lp=Ldusk·R0·g,f=1 (3) 式中S15=1.9828.上述模型公式中的参数g和h由公式(4)得到: (4) 两种时期的Ldusk,g0,h0都随着Tepoch不同而变化,变化尺度为1 h,时间跨度从-24 h到36 h. 值得注意的是原文中作者先设定MLT在0~24变化,并将MLT与λ的关系定义为: (5) 但通过作者论文中生成的模型图像输出结果和公式对比发现,此处作者可能由于疏忽而出现了错误,实际模型应该是先设定λ在0~2π变化,MLT与λ的转换关系是: (6) 2015年6月22日到24日期间的Dstpeak=-204 nT,表明发生了强磁暴.在22日12∶00到24日12∶00期间RBSP-A卫星上EMFISIS仪器测得的电子密度数据如图2所示,图中黑色虚线表示电子密度突变即卫星在此时经过等离子体层顶,由此得到的实际数据与模型计算结果对比如表1所示. “间距”表示卫星测得的实际数据点与模型计算结果的最近点间距,代表误差情况. 同样2016年1月20日至21日处于地磁活动期间,这次磁暴的Dstpeak=-93 nT,表明发生了中等磁暴.期间RBSP-A卫星测得的等离子体层顶位置数据和模型计算结果对比如表2所示. 需要注意的是Dst指数以及模型参数都是按小时变化,本文中当历元时间出现小数时都以四舍五入的方式转化到对应的数值并选取参数. 通过观察这两次得到的卫星数据点与模型计算结果最近点的间距,发现误差较大的几个数据点都出现在9≤MLT≤18时,而该部分区域正是容易形成羽状区的地方.我们将测得的间距数据分为两类,第一类主要是在夜侧,即0≤MLT<9或18 图2 2015年6月22日12∶00到24日12∶00期间RBSP-A测得的电子密度数据Fig.2 Electron density data measured by RBSP-A from 12∶00 on June 22 to 12∶00 on June 24,2015 表1 强磁暴期间RBSP-A卫星测得的等离子体层顶位置与模型计算结果的对比Table 1 A comparison between the plasmapause location measured by RBSP-A satellite during a strong magnetic storm and the calculated results of the model 表2 中等磁暴期间RBSP-A卫星测得的等离子体层顶位置与模型计算结果的对比Table 2 A comparison between the plasmapause location measured by RBSP-A satellite during a moderate magnetic storm and the calculated results of the model 我们发现第二类数据误差相对要大许多,考虑到可能是羽状区在磁暴情况下会发生明显的动态变化,特别是在磁暴剧烈时期.为了更好的研究羽状区并考察模型误差的原因所在,由于RBSP-A的卫星运行半径限制以及存在一定的轨道倾角,我们转而利用在地球静止轨道上运行的LANL卫星数据进行进一步的针对性分析并对模型进行优化改进工作. LANL卫星在地球静止轨道上运行,按照模型演示的结果,一般只有在中等磁暴时的磁暴剧烈时期,羽状区等离子体层顶会延伸到地球静止轨道.在这里我们考察误差的方式稍有所改变,原来选取最近点间距的方式已经不能适用,因LANL卫星运行方向与自转方向一致,当处于磁暴剧烈时期模型的羽状区边界可分为两类,我们把模型在9≤MLT≤12的部分叫做进入羽状区边界,在15≤MLT≤18的部分叫做离开羽状区边界.因为一些进入(离开)羽状区的数据点却与模型中离开(进入)羽状区的边界更为接近,这时再按照最近点间距得到的误差数据就失去科学意义了,改为与模型中对应的进入或离开羽状区边界的最近点间距更加合理. 由于LANL卫星的仪器限制,我们在这里选取的是其上搭载的MPA仪器测得的低能离子密度数据,该数据与RBSP卫星测得的电子密度数据都曾被Goldstein等(2019)用于检验等离子体层顶位置模型.图3是2006年8月19日到21日期间LANL-94测得的低能离子数据,图中黑色虚线代表低能离子密度突变处,即卫星在此时经过等离子体层顶. 通过筛选1998—2006年符合条件的14次中等磁暴事件,并尽量让选取的磁暴事件的Dstpeak比较均匀的分布在-120 nT到-60 nT之间,在分析LNAL系列卫星测得的低能离子密度数据后我们得到64个进出羽状区边界的信息如表3所示.由表中数据得到中等磁暴时模型的羽状区边界与卫星数据点的间距数据平均值为1.81RE,平均误差为27.34%,基于这些数据我们可以开始具体的探讨影响羽状区模型误差的一些因素. 我们将卫星得到的等离子体层顶位置数据点按进入或离开羽状区分成两类数据,再将这两类数据按历元时间分成4个不同时间段.进入和离开羽状区边界的数据按每隔4 h分类的数据点个数和平均值如表4所示,各时段进出羽状区的平均MLT变化情况如图4所示. 图3 2006年8月19日到21日期间LANL-94测得的低能离子密度数据Fig.3 Low-energy ion density data measured by LANL-94 from August 19 to 21, 2006 图4 各时间段进(a)出(b)羽状区MLT分布Fig.4 MLT distribution in (a) and out (b) plume area in each time period 表3 LANL卫星测得数据与模型对比Table 3 Comparison between data measured by LANL satellite and model 续表3 续表3 表4 进出羽状区边界数据点分布Table 4 Distribution of boundary data points in and out of plume 根据图4可以发现每个时间段进出羽状区的平均MLT会随着历元时间发生明显的规律性变化,意味着羽状区会随着磁暴演化过程发生动态演化.从得到的样本数据来看变化趋势为磁暴发生后越接近磁暴峰值Dstpeak时,进入羽状区边界与地球静止轨道交点的MLT越接近12,离开羽状区边界与地球静止轨道交点的MLT越接近15;在达到Dstpeak后,0~4 h内测得的进入羽状区边界与地球静止轨道交点的MLT迅速增大,而离开羽状区边界与地球静止轨道交点的MLT近似保持不变.下面我们将从电场平衡的理论出发分析这个现象的原因,并尝试对模型进行改进. 根据电场平衡理论,Grebowsky(1970)提出在对流电场增强时,在晨昏侧的等离子体层顶会向正午方向转动.所以在磁暴逐渐增强并接近Dstpeak的磁暴剧烈时期,羽状区依然会慢慢产生西漂,这一点在上面对图4的数据分析中得到了印证. 当磁暴过了Dstpeak后,地磁活动减弱,羽状区等离子体层顶出现收缩,而且根据已有的实际数据表明这个收缩速度较快.原模型的公式和给出的参数也表明了这一点,如图5中所示,Tepoch>4 h后羽状区就闭合了,进入磁暴平缓时期,图中黑色虚线表示地球静止轨道.而在图4中分析发现0~4 h测得的进入羽状区边界数据大幅上升并向昏侧移动,而离开羽状区的MLT却近似不变,这正说明了这一时间段羽状区会出现迅速收缩和东漂. 图5 模型在Tepoch=4 h(a)和5 h(b)的等离子体层顶示意图Fig.5 The plasmapause location of the model with Tepoch =4 h (a) and 5 h (b) 了解误差产生的原理后,我们将针对这一现象对模型进行优化改进.改进的基本方法是:如分析数据一样,将磁暴剧烈时期,即-12 h≤Tepoch≤4 h,按每隔4小时拆分为4段.在每一段,通过旋转在9≤MLT≤12和15≤MLT≤18的模型并改变一定的曲率,使这两段模型分别在-10 h、-6 h、-2 h和2 h时同地球静止轨道交点的MLT与对应时段测得数据的平均MLT误差小于0.1. 通过不断对原模型进行拟合与修正,在公式(2)的基础上形成了新的4个时间段的改进模型,其中在-12~-8 h时间段采用公式(7): 18≤MLT<24:Lp=Ldusk·R3·g,f=1 00 Lp=Ldusk·R1·g·S-10,f=0.33 16≤MLT≤18:Lp=Ldusk·R-10·h,f=1 MLT=24:Lp=Ldusk·R0·g,f=1 (7) 18≤MLT<24:Lp=Ldusk·R3·g,f=1 00 Lp=Ldusk·R1·g·S-6,f=0.185 16≤MLT≤18:Lp=Ldusk·R-6·h,f=1 MLT=24:Lp=Ldusk·R0·g,f=1 (8) 18≤MLT<24:Lp=Ldusk·R3·g,f=1 00 Lp=Ldusk·R1·g·S-2,f=0.16 15≤MLT≤18:Lp=Ldusk·R-2·h,f=1 MLT=24:Lp=Ldusk·R0·g,f=1 (9) 18≤MLT<24:Lp=Ldusk·R3·g,f=1 00 Lp=Ldusk·R1·g·S2,f=0.2 15≤MLT≤18:Lp=Ldusk·R2·h,f=1 MLT=24:Lp=Ldusk·R0·g,f=1 (10) 改进前后模型在Tepoch= -10 h、-6 h、-2 h和2 h的等离子体层顶对比情况如图6中所示,可以发现改进后的模型与原模型相比,羽状区随着磁暴演化能够产生特征十分明显的动态变化. 最后我们将改进后的模型与LANL卫星测得的64个实际数据点进行误差检验,得到的总误差数据对比如表5所示,按4个时间段分类对比的数据和图像分别如表6和图7所示,可以发现每个时段的改进模型误差都出现了不同程度的下降. 根据表5中的数据,我们得到改进后模型在这些数据点的总平均误差为1.34RE,误差率为20.2%;而原模型在这一时期羽状区的平均误差率为27.34%,改进后的模型使得准确度提升了26%,得到了更好的拟合效果. 表5 改进前后模型误差数据对比Table 5 Comparison of model error data before and after improvement 图6 改进前(a)后(b)模型在Tepoch=-10 h、-6 h、-2 h和2 h的等离子体层顶(分别用绿、红、黑、粉四种实线表示)示意图Fig.6 Before (a) and after (b) improvement, the plasmapause location (represented by green, red, black and pink solid lines, respectively) of the model with Tepoch=-10 h, -6 h, -2 h, and 2 h 表6 改进前后模型误差数据按历元时分类对比Table 6 The model error data before and after improvement are classified and compared according to epoch time 图7 改进前后模型误差数据按历元时间分类对比Fig.7 The model error data before and after improvement are classified and compared according to epoch time 本文利用RBSP-A卫星测得的等离子体层顶位置数据对等离子体层顶位置模型进行了误差检验,为了更好的了解并改善模型在日侧特别是羽状区的误差情况,我们分析了1998年到2006年间的14次中等磁暴下LANL卫星的数据,发现了在磁暴剧烈时期羽状区等离子体层顶产生的西漂、东漂和收缩的动态演化过程.针对这种现象,我们将磁暴剧烈时期按每隔4小时拆分为4个时间段,分别拟合得到了4个更加吻合LANL卫星观测数据的改进模型.将改进模型与原模型进行比较后,每个时间段的改进模型误差结果相对原模型都呈现出了不同程度的下降,改进后的模型在磁暴剧烈时期羽状区的总平均误差下降了26%. 改进模型不仅能在数值上和实测数据更加吻合,同时也更加准确的反映了在磁暴达到峰值前后的等离子体层顶羽状区的动态演化过程. 目前改进模型给出的是中等磁暴下的结果,但无论何种磁暴,在地磁活动剧烈时期羽状区的西漂、东漂以及收缩过程仍然是可以确定的,因此对于强磁暴条件下的情况具有一定的借鉴意义.由于样本数据量的限制,模型的改进工作还不够细化,改进模型的精确度也需要更多的实际数据支持,这是未来的研究工作所要考虑的. 致谢感谢NASA (National Aeronautics and Space Administration,美国航空航天局)提供的RBSP-A卫星与LANL卫星数据,感谢京都大学世界地磁数据中心提供的Dst指数.感谢两位评审专家对本文提出的宝贵意见.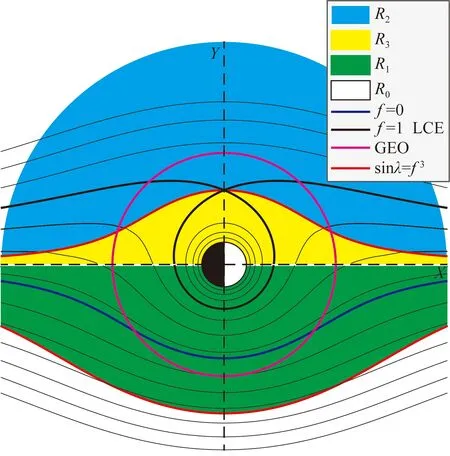
1.2 RBSP-A卫星数据检验模型误差

2 模型的优化改进
2.1 LANL卫星数据



2.2 理论依据和修改方法
2.3 改进后的模型和误差对比
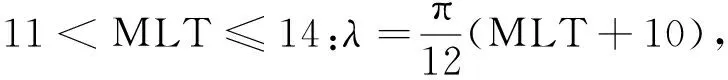


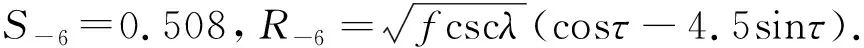

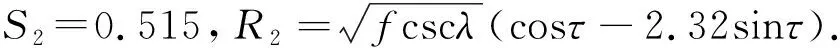


3 结论
