张力腿平台涡激运动特性数值模拟与模型试验研究*
2021-02-23田辰玲刘明月王世圣肖龙飞
田辰玲 刘明月 王世圣 肖龙飞
(1. 上海交通大学海洋工程国家重点实验室 上海 200240; 2. 上海交通大学三亚崖州湾深海科技研究院 海南三亚 572024;3. 中海油研究总院有限责任公司 北京 100028)
张力腿平台是一种海上油气开发装备,利用半顺应半刚性的结构特性产生远大于平台自重的浮力,与预张力达到平衡状态,从而提供安全可靠的作业环境。张力腿平台的立柱多为圆柱型结构,在一定来流条件下其后方会发生交替性的漩涡脱落,在立柱两侧形成脉动压力差。脉动压力可分解为顺流向的脉动阻力和垂直于流向的脉动升力。平台在脉动升力的作用下发生周期性横向运动,是涡激运动的主要组成部分。平台在顺流向会在某个平衡位置做小范围的脉动,此外整个平台在脉动力矩的作用下还会发生周期性首摇运动。对于深吃水海洋浮式结构物,由于立柱浸没深度的增加,其在深海海流作用下会受到更大的脉动力,产生更显著的涡激运动,加剧锚泊和立管系统的疲劳损伤,大大降低其疲劳使用寿命。因此,学术界和工程界对此问题十分关注。
近年来对浮式结构物的涡激运动的研究手段主要为模型试验和数值模拟方法。国内外学者对多立柱浮式平台涡激运动做了丰富的试验研究,针对半潜式平台,通过研究不同参数对其涡激运动的影响,如吃水比[1]和流向角[2-4]等,从而达到优化平台设计的目的。与半潜式平台的方形立柱不同的是,张力腿平台的立柱由四圆柱组成,其流场结构和流固耦合现象更为复杂。相较于半潜式平台的涡激运动特性研究,对张力腿平台涡激运动问题的研究较少。Tan等[5]对比了张力腿平台在光体和安装附体2种布置条件下的涡激运动特性,发现张力腿平台在不安装任何附体时表现出更为显著的涡激运动。Gonçalves等[6]研究对比了四圆柱(代表张力腿平台)、四方柱(代表半潜式平台)和四菱柱结构在不同流向角和不同立柱间距比情况下的涡激运动响应,结果表明四圆柱结构的涡激运动响应最为显著。Tian等[7]开展了附体和质量比等因素对张力腿平台涡激运动影响的模型试验,结果表明,附体的存在会在一定程度上抑制平台的涡激运动响应,此外当Sc(Scruton,简称Sc)数低于0.1时,横向运动响应并不会随着质量比的增大而减小。
随着计算机技术的发展,计算流体力学方法(Computational Fluid Dynamics,简称CFD)被广泛用于研究涡激运动问题,逐渐成为不可或缺的研究手段,可与模型试验结果进行相互验证[8],避免由于模型试验成本较高而无法进行全面的参数敏感性分析的不足。Kim等[9-10]利用三维计算流体力学方法研究了半潜式平台涡激运动响应问题的数值敏感性,结果表明应用延迟分离涡模拟(Delayed Detached Eddy Simulation,简称DDES)方法可以得到更为准确的涡激运动响应幅值预报。此外,还有不少研究学者对比分析了采用模型试验和数值模拟2种方法对半潜式平台的涡激运动预测结果的影响[11-13]。
张力腿平台的垂向运动性能虽然较好,但在水平面内会受到较大的流体力作用,诱发显著的涡激运动响应,加剧张力腿平台立管和系泊系统的疲劳损伤,降低其疲劳使用寿命,从而影响平台的作业安全。目前业内针对张力腿平台在不同流向角下的涡激运动特性的研究相对缺乏。为了全面了解张力腿平台在典型流向角下的涡激运动响应特性,本文以原计划用于开发南海流花16-2油田群的某张力腿平台为研究对象,通过开展不同网格类型的数值模拟和拖曳水池模型试验来对比研究了张力腿平台在均匀流作用下的涡激运动性能,总结其在不同流向角下的涡激运动响应特性,以期为张力腿平台的研究与设计提供参考。
1 涡激运动主要参数
影响涡激运动最重要的参数之一是无量纲参数折合速度Ur,其定义如下:
(1)
式(1)中:U为来流速度,m/s;D为结构物特征尺度,此为立柱直径,m;Tn为张力腿平台横向运动固有周期,s。
分析涡激运动响应幅值时通常选择其无量纲标称值来描述特性,即
(2)
(3)
式(2)、(3)中:σ(Ay)为平台横向运动幅值Ay的标准差,m;σ(Ayaw)为首摇幅值Ayaw的标准差,(°);Aynom为Ay的无量纲标称值;Awnom为Ayaw的无量纲标称值,(°)。
通常流体力的无量纲形式分别用阻力系数和升力系数来表示,其定义如下:
(4)
(5)
式(4)、(5)中:FX(t)、FY(t)分别为作用在平台X、Y方向的流体力,N;ρ为流体密度,kg/m3;Ap为平台在垂直于来流方向上的投影面积,m2。
(6)
(7)
式(6)、(7)中:i为统计时历中采样数据的编号;n为采样数据的个数总和。
2 数值模拟与模型试验的分析模型
2.1 数值模型
2.1.1求解方法
本文采用CD-adapco公司的STAR-CCM+软件对张力腿平台的涡激运动进行数值模拟研究。基于Spalart-Allmaras(简称SA)湍流模型的Detached Eddy Simulation(简称DES)方法求解湍流流动,即边界层内的流动采用SA湍流模型的雷诺时均方法进行求解,边界层外的流动采用Large Eddy Simulation(简称LES)方法求解。
2.1.2计算域与边界条件
本文建立数值模型时,采用缩尺比为1∶50的张力腿平台模型,平台具体参数见表1。为了避免侧壁效应,数值模型中计算域大小取18B×12B×6T(B为平台宽度,m;T为吃水,m)。Lee等[14]对半潜式平台的绕流问题的数值研究中采用的计算域范围为6B×4.5B×2.8T,其数值结果与模型试验吻合良好,因此可认为本文采用的计算域足够大。
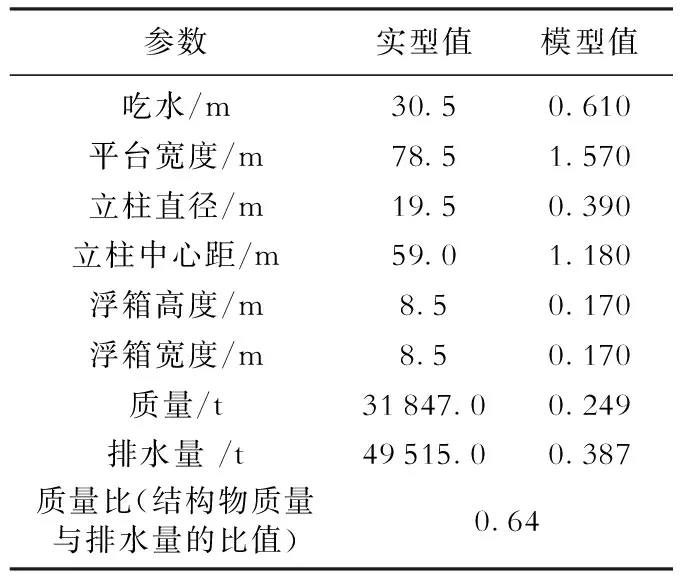
表1 本文张力腿平台主尺度Table 1 Principle dimensions of the TLP in this paper
边界条件为速度入口,压力出口,计算域2个侧壁及上下表面均采用对称面边界条件,平台表面为物面无滑移边界条件(图1)。
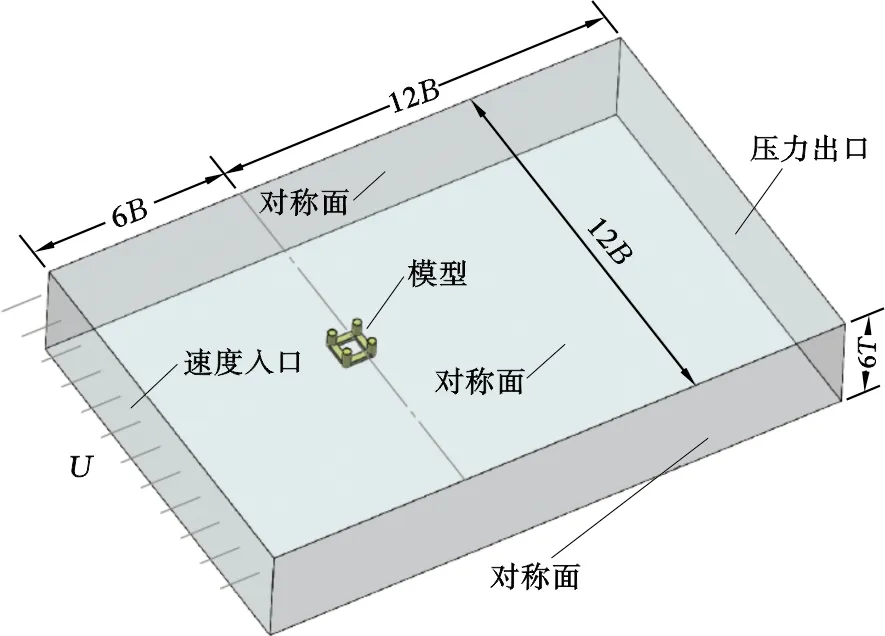
图1 本文张力腿平台的计算域与边界条件Fig .1 Computational domain and boundary conditions of the TLP in this paper
2.1.3网格收敛性验证
采用六面体网格和多面体网格2种网格类型进行数值模拟研究。以六面体网格为例,整个计算域及平台表面的网格划分情况见图2。平台的贴体网格采用边界层网格,且壁面第一层网格的无量纲距离(y+)的均值小于1。平台周围和尾流场的网格适当加密,以准确求解平台周围梯度较大的流场及捕获尾流场的涡泄形态。沿平台展向的网格在平台吃水处进行加密处理。
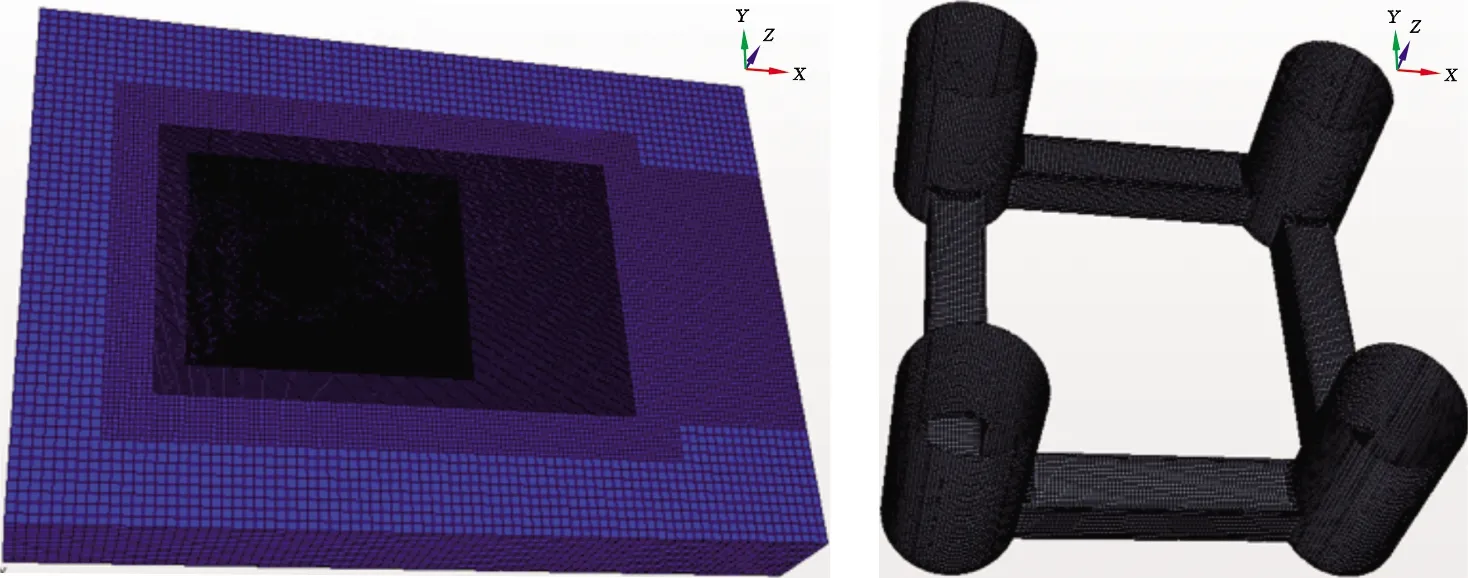
图2 六面体网格的计算域(左)和平台表面的网格(右)Fig .2 Whole computational domain(left) and hull surface for trimmer mesh(right)
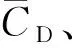
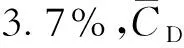
由以上结果可知时间步长对结果影响较小,因此可直接采用Δt/Tn=0.005对多面体网格进行网格数量(分别为43万、108万、256万和566万)收敛性验证。结果表明,随着网格数量的增大,各个参考值的相对变化率逐渐减小。因此多面体网格选择256万网格数量的算例形式。
2.2 模型试验
2.2.1模型及试验装置
与数值模型保持一致,模型试验中采用缩尺比为1∶50的张力腿平台模型。该平台的涡激运动模型试验在拖曳水池中开展,水池有效工作尺寸为110 m×6 m×3 m。拖曳水池配套的拖车最大速度可达5 m/s,速度可调节精度为0.001 m/s,满足涡激运动试验对流速的要求。
涡激运动静水拖曳试验装置如图3所示。坐标系及来流角度定义如图4所示,其中α为流向角,(°);O-XY为大地坐标系,o-xy为随体坐标系。试验过程中通过旋转模型的方式达到改变流向角的目的。利用空气轴承系统和等效水平系泊系统模拟张力腿平台在均匀流中的涡激运动响应。

图3 本文张力腿平台涡激运动试验装置Fig .3 Setup for VIM tests of the TLP in this paper
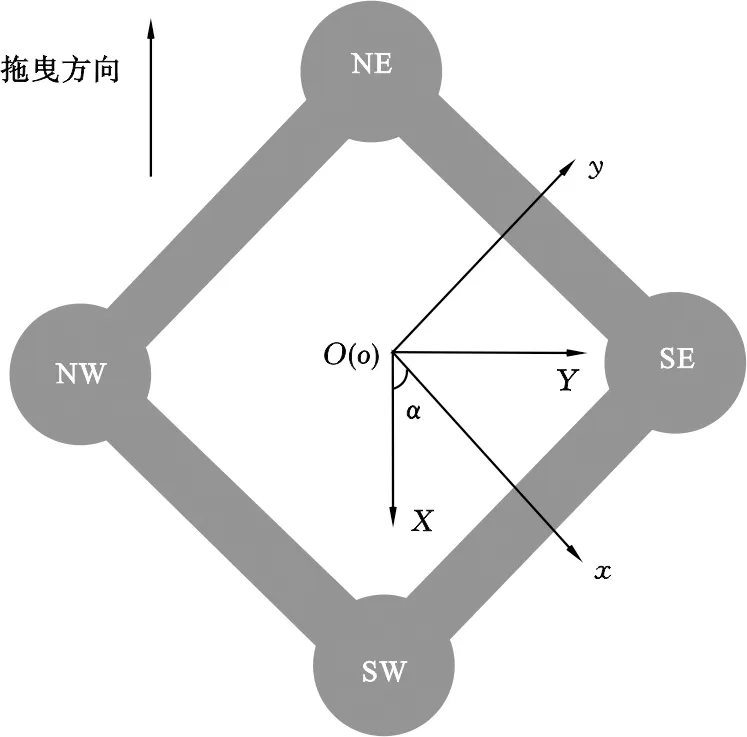
图4 本文张力腿平台模型试验的坐标系及来流角度定义Fig .4 Coordinate and current incidence in model tests of the TLP in this paper
空气轴承系统主要由空气轴承、光滑平板、导气管和气泵等组成。光滑平板固定在拖车的中央桥架上,可在一定范围内上下移动,以便调节平板的高度来适应模型的吃水。空气轴承安装在平台的甲板上,其出气面与光滑平板的光滑面保持悬浮状态,两者之间的摩擦力基本可以忽略,保证平台在试验过程中的自由运动。通过调节此装置可准确模拟张力腿平台的质量比,即将光滑平板固定于合适的高度使平台达到其设计吃水,平台会受到来自于平板的压力,此为垂向预紧力,进而使其满足质量比的要求。此外,试验装置限制了平台垂直面内的运动,即不考虑横摇、纵摇和垂荡,平台仅在水平面内运动,即为涡激运动的主要表现形式。模型的运动通过非接触式光学六自由度运动测量系统来捕捉。
试验中采用等效水平系泊系统模拟实际平台的系泊特性,为平台提供水平回复力,使模型水平面运动的固有周期与实际平台的固有周期满足缩尺比开方的比例关系。等效系泊系统如图5所示,该系统由4根系泊缆组成,每根系泊缆关于坐标轴对称分布,保证系统的横向与纵向刚度一致。导缆点和系缆点的z向高度一致,且高于水平面,使系泊系统呈水平布置。每根系泊缆均由钢丝绳和弹簧制成,并连接一个单分力传感器,以测量其拉力。单根系泊缆的刚度系数为54.28 N/m,松弛长度为1.08 m,预张力为68.67 N。
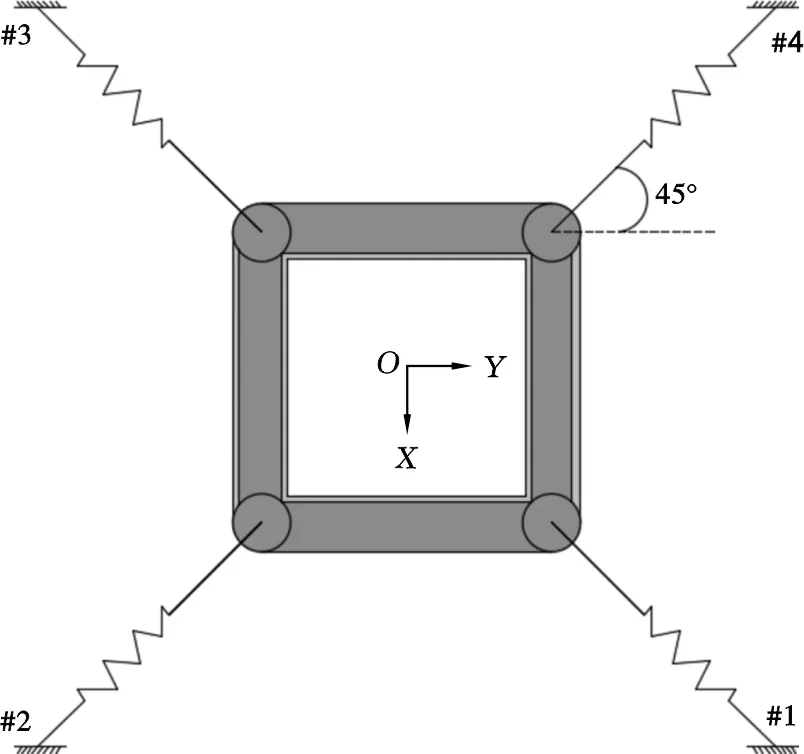
图5 本文张力腿平台等效水平系泊系统布置Fig .5 Layout of the equivalent horizontal mooring system of the TLP in this paper
2.2.2试验工况
在开展涡激运动试验之前,首先进行静水刚度和自由衰减试验得到所需的系统参数值。平台在0°、22.5°和45.0°流向角下横向运动和首摇的固有周期如表2所示。
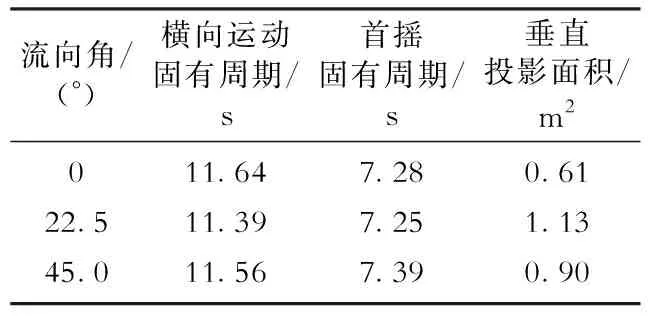
表2 本文张力腿平台涡激运动固有周期及垂直投影面积Table 2 Natural periods of the VIM and the submerged projected areas for the TLP in this paper
拖曳试验探究了张力腿平台在0°、22.5°和45.0°流向角下,折合速度4≤Ur≤12时的涡激运动特性,相应的模型速度范围为0.100 m/s≤U≤0.450 m/s,雷诺数小于3×105,处于亚临界雷诺数范围内,避免了过渡雷诺数区域边界层流态的不确定性。此外,傅汝德数低于0.2,不计自由面的影响。
3 涡激运动结果对比
采用多面体网格和六面体网格分别对张力腿平台的涡激运动进行数值模拟计算,与模型试验值进行对比,多角度分析张力腿平台的涡激运动特性,并验证数值计算结果的可靠性。
3.1 涡激运动响应幅值
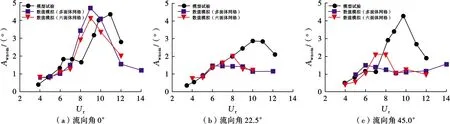
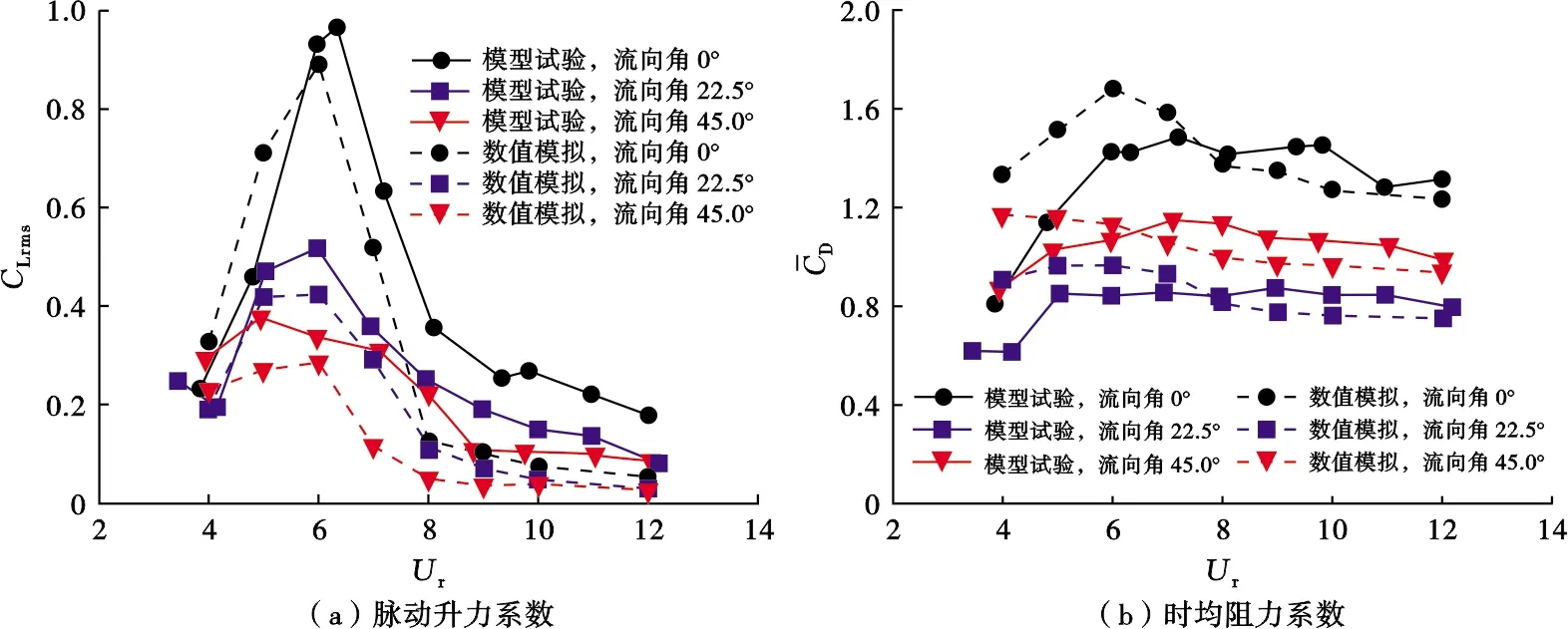
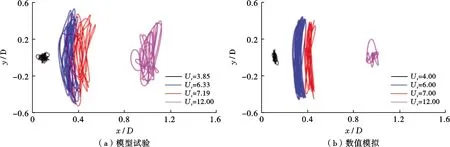
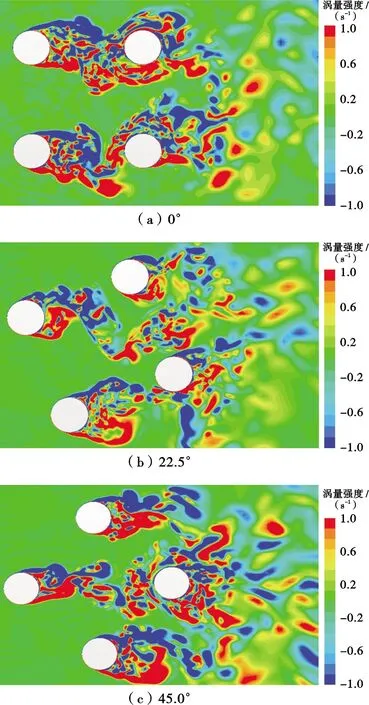
图6为0°、22.5°和45.0°流向角下张力腿平台的横向运动幅值的模型试验与数值模拟结果。0°流向角下,模型试验与数值模拟的横向运动幅值最大值为0.40,均在5 图6 本文张力腿平台横向运动幅值Fig .6 Amplitudes of the transverse motion of the TLP in this paper 因此,无论采用数值模拟方法还是模型试验手段,都能较好地展现张力腿平台的涡激运动特性。但无论在哪个流向角下,模型试验的横向运动幅值均在大折合速度下大于数值模拟结果。此处采用不同网格的数值模拟结果基本一致,说明本文采用的数值模拟方法是可靠的。0°和22.5°流向角下,在Ur>8以后,数值计算得到的横向运动幅值基本都低于0.20,明显小于模型试验值。在0°流向角下,Ur>8后模型试验的横向运动幅值随着折合速度增大而增大,可能发生了驰振现象。45.0°流向角下,数值模拟尤其是多面体网格的数值得到的横向运动幅值在Ur>6后便开始明显低于模型试验结果。 综上所述,张力腿平台的涡激运动无论在哪个流向角下都有明显的锁定区间,为5 图7为0°、22.5°和45.0°流向角下张力腿平台首摇幅值的模型试验与数值模拟结果。在0°流向角时,最大首摇幅值在4.1°~4.3°,锁定区间为8 图7 本文张力腿平台首摇幅值Fig .7 Yaw amplitudes of the TLP in this paper 在数值模拟中,0°流向角的首摇计算结果与模型试验值吻合较好。采用多面体网格和六面体网格的数值模拟得到的首摇幅值均在Ur=9时达到最大值,而模型试验在Ur=11时才出现最大首摇幅值。22.5°流向角下,数值模拟中没有明确的锁定区间,且在Ur>8以后明显低于试验值,尤其是多面体网格的模拟结果。对于六面体网格的模拟结果而言,其曲线与模型试验的吻合程度在Ur≤8的范围内较高,在大折合速度时,模拟的准确度较低。45.0°流向角下,数值模拟结果在大折合速度下的首摇幅值明显低于模型试验值。 综上所述,模型试验和数值模拟均能较好地体现张力腿平台首摇涡激运动特性。虽然多面体网格和六面体网格相较于四面体网格来说均有较高的计算精度,但无论采用多面体网格还是六面体网格,其模拟结果与模型试验的结果均在大的折合速度下有一定的偏差,且数值模拟的首摇幅值偏小。值得一提的是,相对于多面体网格,采用六面体网格的数值模拟结果在更大的折合速度下才出现幅值的降低,故六面体网格的吻合度较高于多面体网格。造成这种现象的主要原因是圆柱绕流问题较为复杂,尤其是对于具有多圆柱结构的张力腿平台,各个圆柱周围的流场存在互相干扰,数值手段捕捉漩涡的能力有限,模拟难度较大。此外,Brouwer等[15]的研究中提到,模型试验中由于水池有效拖曳长度有限,可获得的运动时历较短,因此统计结果具有一定的随机性。这一随机性在CFD分析中也同样存在。 鉴于数值计算中采用六面体网格模拟结果与模型试验结果的吻合度较高,因此以下章节将采用六面体网格的数值模拟结果与模型试验进行对比分析。图8为张力腿平台脉动升力系数及时均阻力系数的数值模拟结果与模型试验结果对比。对比图8a及图6可知,无论在哪个流向角下,脉动升力系数随折合速度的变化曲线与横向运动幅值随折合速度的变化趋势基本一致,即平台在5 图8 本文张力腿平台水动力系数Fig .8 Hydrodynamic coefficients of the TLP in this paper 0°流向角典型折合速度下,xy平面内的运动轨迹如图9所示。其中x/D、y/D分别代表平台的横、纵向无量纲运动。在平台的锁定区间内(红蓝轨迹),其在较小的纵向运动范围内做周期往复性的横向运动,且横向运动范围较大,更偏向于直线型运动。在锁定区间之前,平台的纵向和横向运动范围均较小。在锁定区间之后,平台的运动呈现杂乱无章的特性,随机性较强。 图9 本文张力腿平台平面内的运动轨迹Fig .9 Motion trajectories of the TLP in the plane in this paper 为了深入研究张力腿平台尾流区域的物理形态和流体结构,本文展示了其在0°、22.5°和45.0°流向角,Ur=6的瞬时涡量云图,如图10所示。在均匀流中,张力腿平台的每个圆形立柱两侧均会产生交替的漩涡脱落现象,形成脉动压力差,表现为横向的水平升力和顺流向的阻力。平台在此升力的作用下会产生横向运动响应。由图10可知,0°流向角时,下游的2个立柱均处在上游圆柱的尾流场。22.5°流向角时,右下角的下游立柱全部处于上游立柱的尾流场中,导致上游圆柱的漩涡直接撞击在下游柱体表面,下游圆柱的尾涡长度变小,并有可能产生湍流涡,因此下游立柱会产生较大的脉动升力。另一方面立柱之间的横向距离较短,产生的漩涡的间距相对紧凑,漩涡的相互作用较强,因此产生较大的横向运动。而45.0°流向角时,只有最下游的1个立柱会受到上游立柱尾涡的作用,且因为距离较远,作用力较微弱。此外,平台横向受来流方向影响的宽度明显增大,4个立柱之间的横向间距较大,其各自尾流场的漩涡几乎没有干扰,相互作用较弱,平台所处的整个流场的涡量强度较小,因此45.0°流向角时的横向运动幅值最小。 图10 本文张力腿平台XY平面内的涡量等值线瞬时流场图(Z=T)Fig .10 Instantaneous vorticity contours plots(Z=T)in XY plane for the TLP in this paper 1) 0°流向角下,张力腿平台的横向运动响应最显著,无量纲标称值最大约为0.40, 45.0°流向角的横向涡激运动幅值最小,最大无量纲值约为0.23。无论在哪个流向角下,锁定区间均为5 2) 运动轨迹在锁定区间为趋于直线型的往复运动。锁定区之前的运动范围较小,锁定区之后的运动轨迹随机性增强,表现为杂乱无章的特性。 3) 相较45.0°流向角,0°和22.5°流向角时下游立柱产生较大的脉动升力,从而产生显著的横向运动幅值。 4) 数值模拟计算中,采用多面体网格和六面体网格的模拟结果相差不大,二者与模型试验结果均在较小的折合速度下吻合较好,在大的折合速度下有较大的偏差,且数值模拟计算的响应值偏小。这可能是因为多圆柱结构流场对数值模型的要求较高,且模型试验中大折合速度的时历长度有限。但是不同于多面体网格,采用六面体网格的数值模拟在更大的折合速度下才出现幅值的降低,故六面体网格模拟结果与模型试验结果的吻合度较高于多面体网格。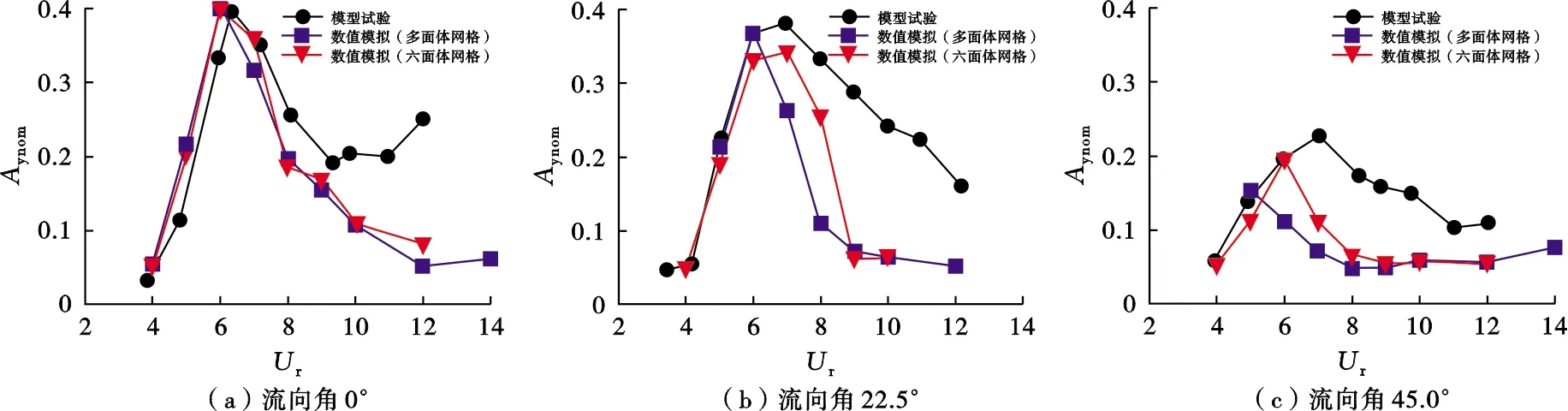
3.2 涡激运动水动力系数
3.3 运动轨迹
3.4 瞬时流场
4 结论
