对角矩阵研究

闫伟文

【摘要】对角矩阵是一种特殊的简单矩阵，具有重要的性质与潜在的应用价值.本文重点总结了对角矩阵的计算、性质及相似对角化，进而推广到分块对角矩阵.

【关键词】对角矩阵;相似对角化;分塊对角矩阵

【基金项目】山西省教育科学十三五规划2020年度互联网+教育研究专项课题+服务人工智能专业发展的大学数学课程体系建设研究（HLW-20145）

对角矩阵作为一种特殊的矩阵，有其独特的运算及性质，是解决线性代数问题的一个重要工具.本文主要从对角矩阵的定义、运算、性质、相似对角化四个方面来研究对角矩阵，进而推广到分块对角矩阵.

一、对角矩阵的定义

形如矩阵A=a11a22ann（主对角线元素aiii=1，2，…，n不全为零，其余元素全为零）的方阵，称为对角矩阵.

二、对角矩阵的运算

1.线性运算.

（1）加法运算.

设对角矩阵A1=a11a22ann，A2=b11b22bnn，则矩阵A1±A2=a11±b11a22±b22ann±bnn，此为对角矩阵的和矩阵，即两个对角矩阵的和为这两个对角矩阵主对角线元素对应求和.

（2）数乘运算.

设对角矩阵A=a11a22ann，k为非零实数，则矩阵kA=ka11ka22kann，此为非零实数与对角矩阵的乘积，即数乘对角矩阵，数要乘到其主对角线的所有元素上.

2.乘法运算.

（1）两个同阶对角矩阵相乘.

设对角矩阵A1=a11a22ann，A2=b11b22bnn，则矩阵A1A2=a11b11a22b22annbnn，即两个同阶的对角矩阵相乘，为其主对角线元素对应相乘，可将其推广到n个同阶对角矩阵相乘.

（2）对角矩阵的幂.

设对角矩阵A=a11a22ann，m为非零自然数，则矩阵Am=a11ma22mannm为对角矩阵的m次幂，即主对角线上各元素的m次幂.

（3）对角矩阵乘同阶矩阵.

设对角矩阵A=a11a22ann，矩阵A1=a11a12…a1na21a22…a2nan1an2…ann，则矩阵

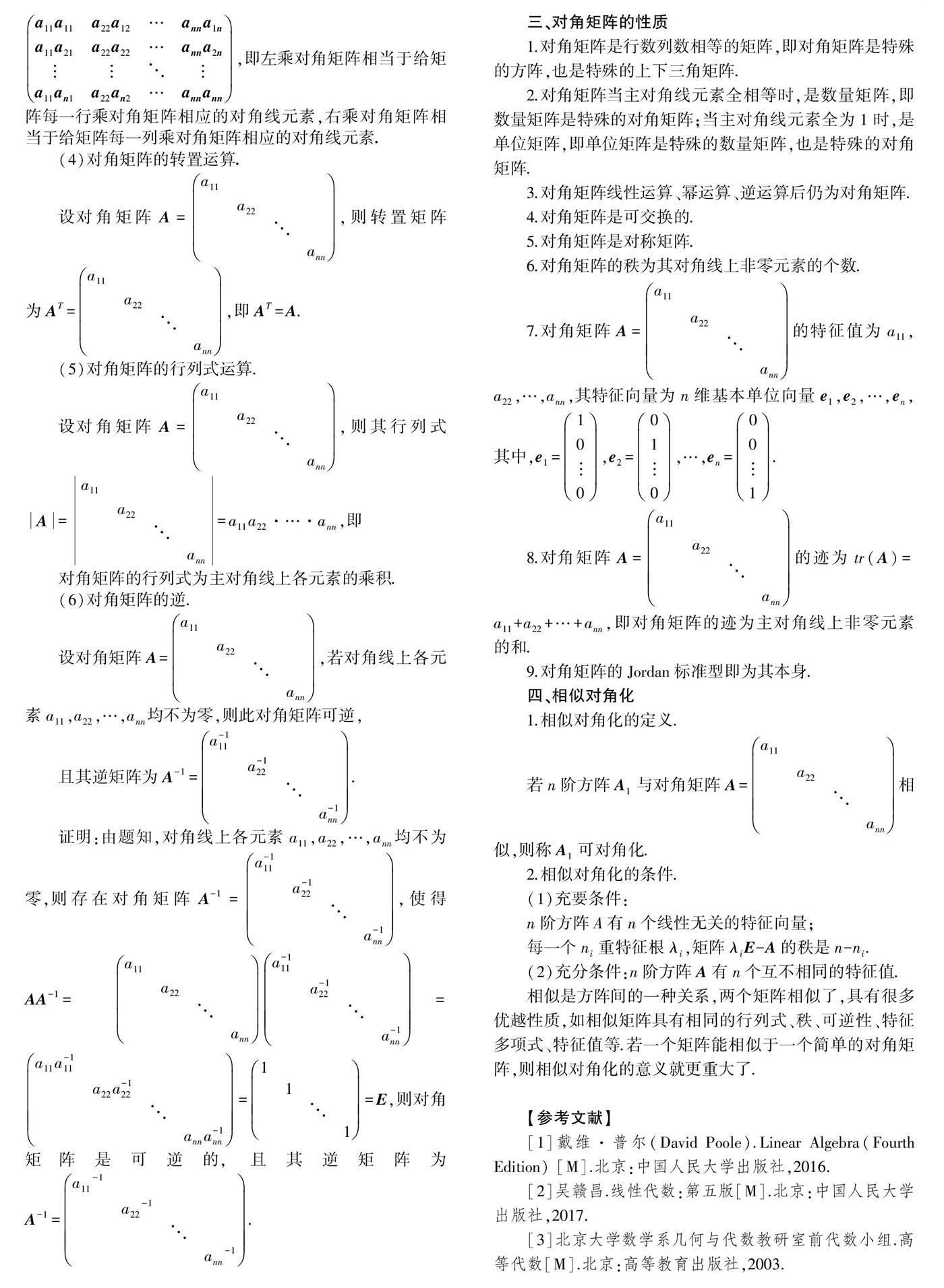
AA1=a11a11a11a12…a11a1na22a21a22a22…a22a2nannan1annan2…annann，A1A=a11a11a22a12…anna1na11a21a22a22…anna2na11an1a22an2…annann，即左乘对角矩阵相当于给矩阵每一行乘对角矩阵相应的对角线元素，右乘对角矩阵相当于给矩阵每一列乘对角矩阵相应的对角线元素.

（4）对角矩阵的转置运算.

设对角矩阵A=a11a22ann，则转置矩阵为AT=a11a22ann，即AT=A.

（5）对角矩阵的行列式运算.

设对角矩阵A=a11a22ann，则其行列式A=a11a22ann=a11a22·…·ann，即

对角矩阵的行列式为主对角线上各元素的乘积.

（6）对角矩阵的逆.

设对角矩阵A=a11a22ann，若对角线上各元素a11，a22，…，ann均不为零，则此对角矩阵可逆，

且其逆矩阵为A-1=a-111a-122a-1nn.

证明：由题知，对角线上各元素a11，a22，…，ann均不为零，则存在对角矩阵A-1=a-111a-122a-1nn，使得AA-1=a11a22anna-111a-122a-1nn=a11a-111a22a-122anna-1nn=111=E，则对角矩阵是可逆的，且其逆矩阵为A-1=a11-1a22-1ann-1.

三、对角矩阵的性质

1.对角矩阵是行数列数相等的矩阵，即对角矩阵是特殊的方阵，也是特殊的上下三角矩阵.

2.对角矩阵当主对角线元素全相等时，是数量矩阵，即数量矩阵是特殊的对角矩阵;当主对角线元素全为1时，是单位矩阵，即单位矩阵是特殊的数量矩阵，也是特殊的对角矩阵.

3.对角矩阵线性运算、幂运算、逆运算后仍为对角矩阵.

4.对角矩阵是可交换的.

5.对角矩阵是对称矩阵.

6.对角矩阵的秩为其对角线上非零元素的个数.

7.对角矩阵A=a11a22ann的特征值为a11，a22，…，ann，其特征向量为n维基本单位向量e1，e2，…，en，其中，e1=100，e2=010，…，en=001.

8.对角矩阵A=a11a22ann的迹为tr（A）=a11+a22+…+ann，即对角矩阵的迹为主对角线上非零元素的和.

9.对角矩阵的Jordan标准型即为其本身.

四、相似对角化

1.相似对角化的定义.

若n阶方阵A1与对角矩阵A=a11a22ann相似，则称A1可对角化.

2.相似对角化的条件.

（1）充要条件：

n阶方阵A有n个线性无关的特征向量;

每一个ni重特征根λi，矩阵λiE-A的秩是n-ni.

（2）充分条件：n阶方阵A有n个互不相同的特征值.

相似是方阵间的一种关系，两个矩阵相似了，具有很多优越性质，如相似矩阵具有相同的行列式、秩、可逆性、特征多项式、特征值等.若一个矩阵能相似于一个简单的对角矩阵，则相似对角化的意义就更重大了.

【参考文献】

[1]戴维·普尔（David Poole）.Linear Algebra（Fourth Edition） [M].北京：中国人民大学出版社，2016.

[2]吴赣昌.线性代数：第五版[M].北京：中国人民大学出版社，2017.

[3]北京大学数学系几何与代数教研室前代数小组.高等代数[M].北京：高等教育出版社，2003.